-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Composite Materials
p-ISSN: 2166-479X e-ISSN: 2166-4919
2021; 11(1): 5-12
doi:10.5923/j.cmaterials.20211101.02
Received: Jun. 22, 2021; Accepted: Jul. 16, 2021; Published: Jul. 30, 2021

Numerical Analysis of Ceramic Mosaic Armor Subjected to Ballistic Impact
Guodong Guo, Shah Alam, Larry D. Peel
Department of Mechanical and Industrial Engineering, Texas A&M University-Kingsville, Kingsville, TX, USA
Correspondence to: Shah Alam, Department of Mechanical and Industrial Engineering, Texas A&M University-Kingsville, Kingsville, TX, USA.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Ceramic mosaics have been used in lightweight armor systems to gain additional multi-hit capacity. However, the tile-to-tile interfaces in ceramic mosaics are inherently vulnerable and thus require special attention. In this research, we present finite element analysis of bilayer armor systems that consist of a ceramic mosaic front layer and a Kevlar-29/epoxy composite backing layer. The objective was to investigate the effect of various tile-to-tile interface designs on the ballistic performance. Two different interface design philosophies are investigated. In the first design, adjacent ceramic tiles are bonded together using epoxy at the interface, considered as a gap filling material. In the second design, adjacent ceramic tiles are separated by metallic webs at the interface, where a titanium honeycomb structure has ceramic tiles inserted into it. The same thickness was imposed for each interface wall to enable a direct comparison of their impact behaviour. Impact location was designated as the central ceramic tile centre. It was found that different interface designs affect stress wave propagation in the armor due to impedance mismatch. The stress state induced in the ceramic tile can be drastically changed and therefore the ballistic resistance of the armor. These results can be used to for the tailoring of mosaic armor systems to achieve the best ballistic performance.
Keywords: Fiber, Impact behavior, Finite element analysis (FEA), Ceramic armor
Cite this paper: Guodong Guo, Shah Alam, Larry D. Peel, Numerical Analysis of Ceramic Mosaic Armor Subjected to Ballistic Impact, International Journal of Composite Materials, Vol. 11 No. 1, 2021, pp. 5-12. doi: 10.5923/j.cmaterials.20211101.02.
Article Outline
1. Introduction
- Ceramic materials have been extensively used in armor designs since the 1960s [1]. Initially, ceramics attracted the interest of armor designers because of their innate superior mechanical properties such as high hardness, high compressive strength and low density. A common practice in modern armor design is to integrate a ceramic front layer with a ductile backing layer to form a bilayer integral armor system [2-5]. The role of the ceramic front layer is to blunt and shatter the intruding projectiles, while the role of the backing layer is to absorb the residual kinetic energy of the projectile and maintain the integrity of the armor system. The traditional bilayer armor system has served as a baseline for more advanced armor designs in recent years [6-7]. However, it is an unfortunate fact that armor with the best single hit ballistic resistance usually do not possess the best multi-hit performance.Mosaic armor has been developed to provide protection for the condition where multi-hit is a priority concern. In mosaic armor, multiple ceramic tiles are assembled in a densely patterned array, thus the destruction of one tile would cause minimal damage to the rest of the tiles through curbing the crack propagation. In recent years, there has been a considerable interest in the improvement of mosaic armor to achieve an optimal ballistic resistance. Through measuring the depth-of-penetration into a polycarbonate block, Hazell et al. [8] found that the ballistic resistance of a silicon carbide square tile increases as the tile size increases from 33 mm to 85 mm. Jiusti et al. [9] studied the influence of various gap-filling materials on the ballistic impact performance of alumina-based mosaic amour. They found that the use of an epoxy as a gap-filling material resulted in a greater preservation area than without any gap-filling material. Hu et al. [10] compared the ballistic performance of ceramic mosaic armor with various mosaic geometries. The geometries included circular, hexagonal and square shapes. The armor tested by Hu et al. [10] are full scale armor as each of them contains a composite backing plate. Seifert et al. [11] studied the dependency of the ballistic performance of ceramic mosaic/metal armor on inter tile gap width and projectile impact position. A remarkable observation in their tests was that a better resistance was observed when impacted at the interface than at the central tile when the gap width is zero. It is noted that a common procedure during the fabrication of mosaic armor is to fill an adhesive at the interface between different tiles after which are appropriately arranged. Another emerging design philosophy in mosaic armor is to separate individual ceramic tile by metallic webs which are usually made of a monolithic structure and the ceramic tiles are considered as inserts. The effect of tile web topology on the armor penetration behavior in a hybrid aluminium/alumina structure was investigated by Wadley et al. [12]. An et al. [13] designed a hybrid armor structure with ceramic tiles inserted in a titanium honeycomb that was fabricated directly by removing materials from a titanium block. Zhao et al. [14] systematically compared the ballistic resistance of a metallic plate backed monolithic ceramic armor and a metallic plate backed mosaic armor enhanced by a honeycomb structure.The aforementioned two types of mosaic armor (epoxy filler & titanium web) differ only in the design of the interface yet lead to completely different manufacturing processes. Given that the tile-to-tile interface is always the most vulnerable area in mosaic armor, it is imperative to compare the ballistic response of these two types of armor, which is the objective of this paper. Experimental work reported in literature are always scattered and the testing conditions including the material, target geometry and projectile type are always different, therefore it is crucial to impose the same impact condition on each, to gain a meaningful comparison. On the other hand, it is acknowledged that in real ballistic tests, it is difficult to precisely control the impact location of a mosaic armor. These shortcomings could be successfully minimized by a validated numerical model.Numerical simulation of ceramic armor systems has mostly focused on conventional bilayer structures [15,16], while that of mosaic armor is rare. In our previous study [17], the ballistic impact performance of a mosaic armor and a monolithic armor were compared using a simplified finite element (FE) model. In this paper, a refined 3D finite element model for integral mosaic armor is developed for the purpose of comparing the performance of two different interface designs. The ceramic tile geometry reported by Jiusti et al. [9] is employed for both armor systems. In the first design, an epoxy similar to that used by Jiusti et al. [9] is assigned as the gap filling material. In the second design, a honeycomb structure made of a titanium alloy as was used by An et al. [13] is assigned to separate individual tiles. The gap filling material and the honeycomb structure are modelled using 3D solid elements to allow an accurate stress transmission in the thickness direction. The ceramic mosaics are backed by a Kevlar 29/epoxy composite plate. APM2 7.62 mm projectiles are used to impact the integral armor. The 3D FE model is validated by comparison with a real ballistic testing. Ballistic performances of the armor are then examined in detail.
2. Finite Element Modelling
2.1. Model Description
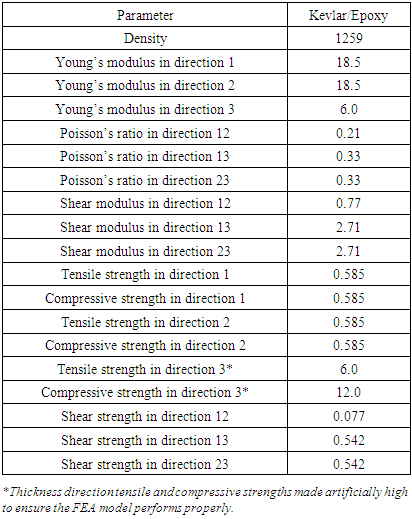
- A schematic of the problem statement is exhibited in Fig. 1. Major components in the mosaic armor system include hexagonal ceramic tiles (Al2O3) with 30 mm long edges and 8 mm thickness, a gap-filling material, and a backing plate. The dimensions of the ceramic tiles were chosen based on the tested armor reported in Ref. [9]. However, in their experiments, the armor was supported by an aluminium block to facilitate the depth of penetration (DOP) test. Since DOP tests with semi-finite backing blocks could not reflect real bonding conditions between the ceramic tiles and the relatively thinner backing plates in real armor, in the current study a thin backing plate made of a high-performance Kevlar-29 fiber reinforced composite is assumed. The backing plate has a dimension of 200 mm × 200 mm × 8 mm. The gap-filling material is made of a monolithic component with a thickness of 1.5 mm. This gap dimension was also selected based on the specimen reported in Ref. [9]. In the numerical model, the distinction between an epoxy-filled armor and a honeycomb-inserted armor is based solely on assigned material properties. In addition, it is known that the ballistic behavior of lightweight armor systems depends on different impact projectiles. In the current model, the 7.62 mm APM2 projectile is used. It consists of a very hard steel core (5.25 g), a gilding metal jacket (4.21 g), a lead nose element (0.78 g) and a lead base filler (0.5 g) [18].
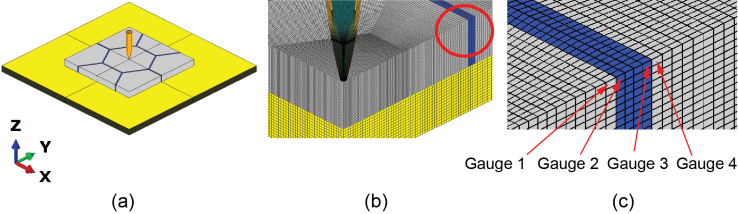 | Figure 1. Schematic of a mosaic armor and gauge locations for stress analysis |
2.2. Material Models
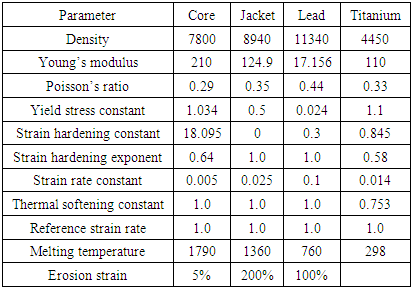
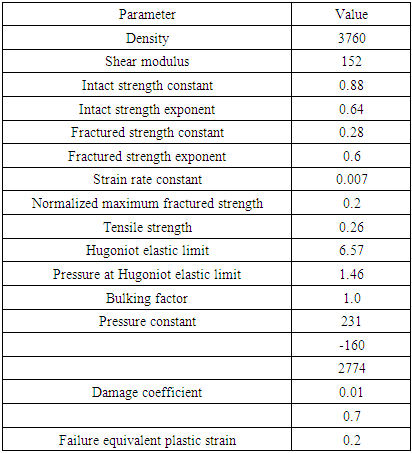
- The projectile consists of three different materials as stated earlier. The Johnson Cook (JC) plasticity model [19] was selected to characterize the material behavior of all the three constituents. The JC model can predict the material response of metallic materials subjected to a high strain rate during a high velocity impact. It is commonly used in ballistic impact simulations due to its uncoupled approach in calibrating material parameters. The JC model parameters for the projectile core, jacket and lead are given in Table 1.
|
|
|
2.3. Model Validation
- The validity of the current numerical model was attested by comparing simulation results of a monolithic bilayer armor with the ballistic testing. In the ballistic experiments, bilayer alumina ceramic armor backed by Kevlar-29/epoxy composite plate were impact against 7.62 mm APM2 projectiles. A picture of the specimen before and after a penetrated impact is shown in Fig. 2. The specimen tested was also covered by a thin Kevlar-29 sheet bonded onto the top surface of the ceramic tile, which is not shown here. The dimension of the ceramic tile used in the tests was 100 mm × 100 mm × 12.7 mm. The dimension of the composite backing plate was the same as that used in the current simulation. The ballistic limit of the monolithic bilayer armor from numerical simulation was 1100 m/s, very close to the experimental result of ~1090 m/s. After the monolithic bilayer model was validated, the thickness of the ceramic tile was reduced to 8 mm for the current simulation and a honeycomb shaped gap-filling structure was added as a design parameter.
 | Figure 2. (a) APM2 projectile; (b) Alumina/Kevlar-29 composite armor system; (c) Alumina fragments collected after impact; (d) Kevlar-29 composite backing plate after impact |
3. Results and Discussion
- The ballistic resistance of the two armors with different interface designs are firstly compared. It is known that the ballistic resistance of a mosaic armor is generally less than that of a corresponding monolithic armor due to the reduced ceramic size. As a reference, the ballistic resistance of a monolithic bilayer armor, that with the same thickness but larger ceramic tile size is also presented as a reference.
3.1. Ballistic Resistance
- When impacted at the canter of the ceramic tile, a relation between the impact velocity vi and the residual projectile velocity vr is plotted in Fig. 3. In each of the armor designs, the target shows a typical ballistic behavior, that the projectile would not fully perforate the target until a critical velocity is achieved. Immediately above the ballistic limit, the residual velocity of the projectile increases sharply. It can be seen that the ballistic limit of the three armor increase in the order of epoxy-filled (525 m/s), honeycomb inserted (625 m/s) and monolithic armor (675 m/s). The ballistic limit of the honeycomb inserted armor is close to that of the monolithic armor. Actually, the ballistic limit of a mosaic armor increases as the tile size increases, and eventually saturates at a critical value equivalent to that of a monolithic armor [8]. The simulation shows that for the honeycomb inserted armor, the studied tile size is very close to the critical limit. On the contrary, for the epoxy filled armor, since its ballistic limit is well below that of a monolithic armor, further increasing in the tile size will drastically improve its ballistic resistance.
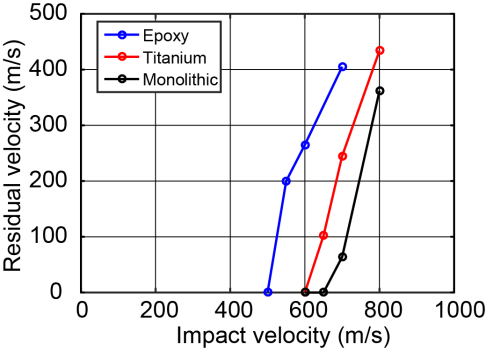 | Figure 3. Residual velocity versus impact velocity relationship of the three armor |
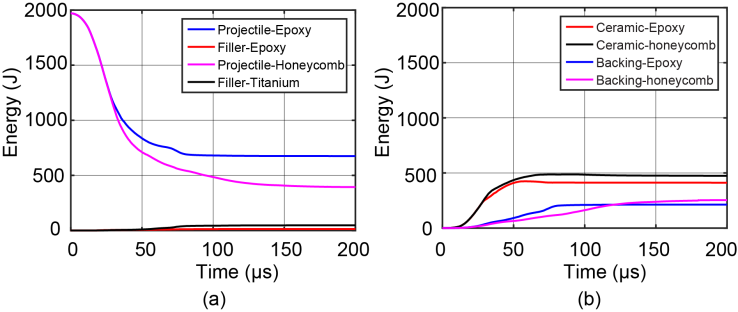 | Figure 4. (a) Projectile kinetic energy history and energy dissipated by the gap-filler in the two armor. (b) Energy absorbed by the ceramic tile and the backing plate in the two armor |
3.2. Stress Analysis
- This section presents a stress analysis of the two types of mosaic armor when impacted at the center of the ceramic tile at 600 m/s. It is seen that the gap-filler alters the energy dissipated by each individual component. Therefor a wave tracking is performed to investigate the role of the gap-filler.When the armor is impacted by the projectile, a dilatational wave is initiated at the impact site and propagates outward. For an unbounded medium the wave velocity C can be calculated as
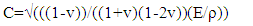 | (1) |
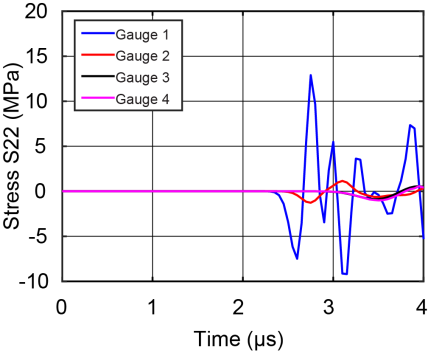 | Figure 5. Stress history at the four gauges in epoxy-filled mosaic armor |
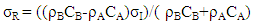 | (2) |
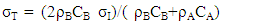 | (3) |
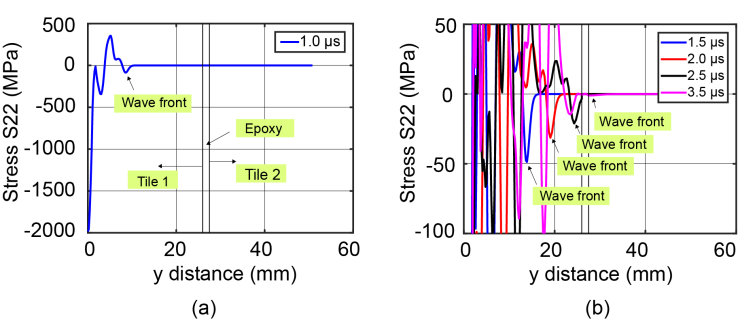 | Figure 6. Stress distribution along y-axis around 2.5 µs |
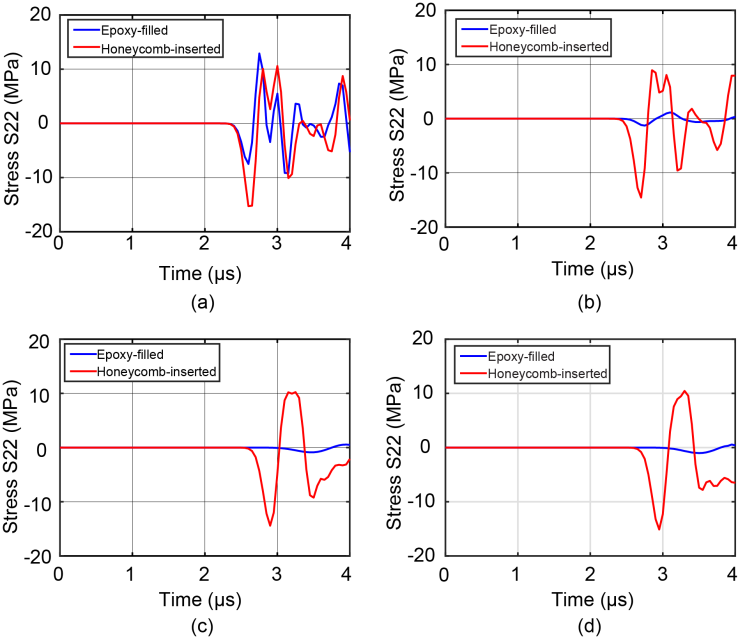 | Figure 7. Stress history at (a) gauge one; (b) gauge two; (c) gauge three; (d) gauge four |
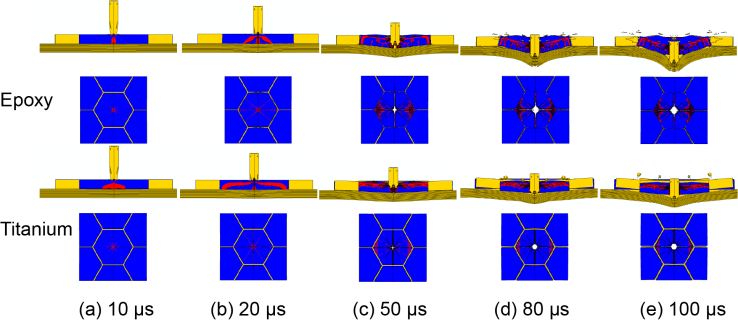 | Figure 8. Deformation of the two types of armor at different time instants |
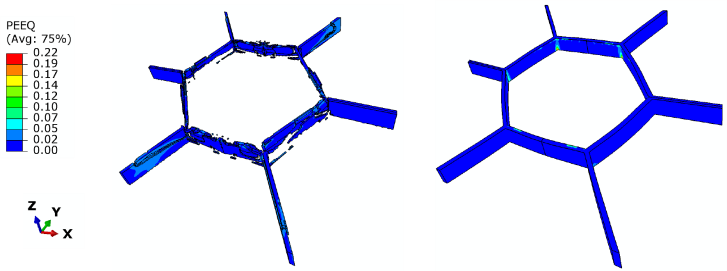 | Figure 9. Deformation of epoxy filler and titanium honeycomb in the two armor at 100 µs |
4. Conclusions
- In this paper, we developed a 3D finite element model for mosaic armor and investigated ballistic performance of two mosaic armor systems with different interface designs. It was found that when the armor is impacted at the center of a ceramic tile, the ballistic performance is strikingly different for different gap-filling material. Although the tile-to-tile interface was not directly involved in contact with the projectile, the ballistic limit of the titanium honeycomb-inserted armor shows 19% higher than the epoxy filled armor. While the interface material itself only absorbs a very small portion of the kinetic energy from the projectile, it exerts influence on the ballistic behavior of the armor through changing the energy absorption capability of other components, including the ceramic tile and the backing plate. A stress wave analysis indicates that the stress transmitted to adjacent tiles through the titanium honeycomb is higher than through the epoxy. The stress wave transmission enables more kinetic energy to be absorbed by adjacent tiles. These results have practical values for the design of mosaic armor, i.e., the interface material can be considered as a design parameter to be tailored, with the objective of increasing single hit impact resistance through transmitting stress wave to adjacent tiles while keeping it within a limit so as not to induce fracture thus compromise its multi-hit resistance.
ACKNOWLEDGEMENTS
- This work was supported by the Army Research Office (ARO) Grant Award Number W911NF-18-1-0478.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML