-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Composite Materials
p-ISSN: 2166-479X e-ISSN: 2166-4919
2019; 9(3): 53-59
doi:10.5923/j.cmaterials.20190903.01

A Conical Shell Theory of Hybrid Anisotropic Materials
1School of Architecture, University of Utah, Salt Lake City, USA
2Yeung Nam University, Tae Gu, Korea
Correspondence to: Chung S. W., School of Architecture, University of Utah, Salt Lake City, USA.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

We start with the unique coordinate system of a conical shell and the generalized Hook’s law of a three dimensional anisotropic body which is subjected to 6 different stresses and strains together with 21 elastic coefficients. Applying equilibrium and stress displacement equations and non-dimensionalize all the variables before asymptotically expanding, we are now allowed to perform the asymptotic integration process which will derive the first approximation theory of an anisotropic conical shell. The theory is valid for anisotropic non-homogeneous materials, which can be applied to the layered walls of conical shells with different materials. A choice of small length scale allows a system of differential equations accurately formulated for different loading and boundary conditions. The derived differential equations of homogeneous isotropic material are equivalent to classical theory.
Keywords: Conical Shell, Three Dimensional Anisotropic Element, Non-Homogeneous Anisotropic Materials, Generalized Hook’s Law, Boundary Layer, Asymptotic Integration, Classical Shell Theory
Cite this paper: Chung S. W., Ju Gisu, A Conical Shell Theory of Hybrid Anisotropic Materials, International Journal of Composite Materials, Vol. 9 No. 3, 2019, pp. 53-59. doi: 10.5923/j.cmaterials.20190903.01.
Article Outline
1. Introduction
- The use of composite materials have been wide spread over last 30 years from the aerospace vehicles to civil engineering structures, the materials possess such characteristics as high strength/density and properly controllable modulus/density ratios and they are generally composed of filaments and matrix materials. The filaments are embedded in the matrix materials to give additional stiffness and high strength.The cylindrical, spherical and conical shell theories that we develop in our previous articles are common to liquid oxygen storage tanks of outer space rockets, orbital shuttles as well as liquid storage tank and building structures. The authors already developed and formulated almost all of necessary cylindrical and spherical shell theories of multiple mixture (hybrid) anisotropic materials. Details are published in various journals as shown in the References.
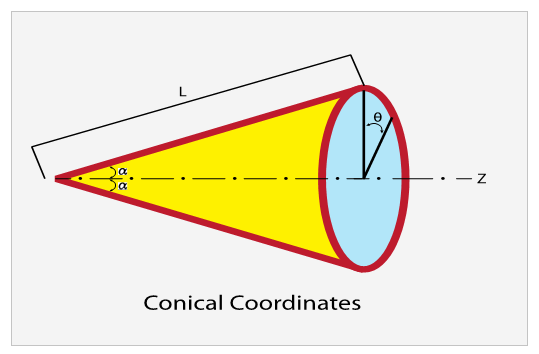 | Figure (1). Coordinates |
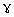 , is the angle between major elastic axis of the material and reference axis (see Figures 2 and 3). The variation in properties in the direction of the thickness implies non-homogeneity of the material and composite structures must thus be analyzed according to theories, which allow for non-homogeneous anisotropic material behavior.
, is the angle between major elastic axis of the material and reference axis (see Figures 2 and 3). The variation in properties in the direction of the thickness implies non-homogeneity of the material and composite structures must thus be analyzed according to theories, which allow for non-homogeneous anisotropic material behavior. 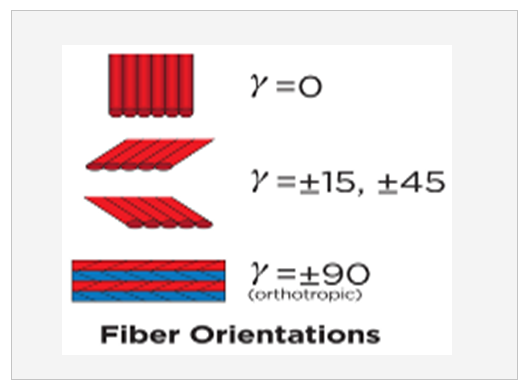 | Figure (2). Fiber Orientation and Laminates |
2. General Anisotropic Conical Shell Theory
- Based on a non-homogeneous, anisotropic volume element of a conical body with longitudinal, circumferential (angular) and radial coordinates being noted as z, Ө and r, respectively, and subjected to all possible stresses and strains (Figure [1].). The cone occupies the space between a ≤ r ≤ a + h and the edges are located at L= 0 and L = L0. Here, a is the inner radius, h the thickness and L the cone length.Assuming that the deformations are sufficiently small so that linear elasticity theory is valid, the following equilibrium and stress-displacement equations [Equations (2.1) and (2.2)] will govern the problem:
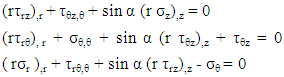 | (2.1) |
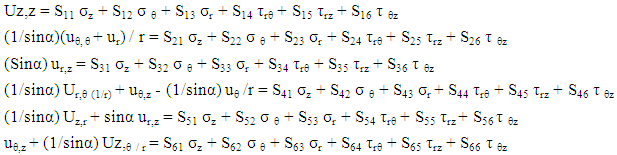 | (2.2) |
 are the displacement components in the radial, circumferential and longitudinal directions, respectively but all measured by normal radius of curvature, therefore must be adjusted by the conical angle α.
are the displacement components in the radial, circumferential and longitudinal directions, respectively but all measured by normal radius of curvature, therefore must be adjusted by the conical angle α.  are the normal stress components in the same directions and
are the normal stress components in the same directions and 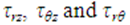 are the shear stresses on the
are the shear stresses on the 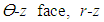 face and
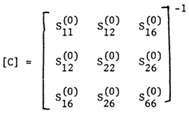
face and 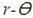 face, respectively (Figure 1). A comma indicates partial differentiation with respect to the indicated coordinates. The Sij’s (i , j = 1, 2,…, 6) in (2.2) are the components of compliance matrix and represent the directional properties of the material. The compliance matrix is symmetric, Sij = Sji.Complete anisotropy of the material is allowed for, making 21 independent material constants. We are not allowed to illiminate any of those components since the material properties depend on the manufactures set up, or, in the case of aerospace vehicles, a different gravity environment. The components can be expressed in terms of engineering constants as follows:
face, respectively (Figure 1). A comma indicates partial differentiation with respect to the indicated coordinates. The Sij’s (i , j = 1, 2,…, 6) in (2.2) are the components of compliance matrix and represent the directional properties of the material. The compliance matrix is symmetric, Sij = Sji.Complete anisotropy of the material is allowed for, making 21 independent material constants. We are not allowed to illiminate any of those components since the material properties depend on the manufactures set up, or, in the case of aerospace vehicles, a different gravity environment. The components can be expressed in terms of engineering constants as follows: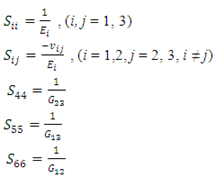 | (2.3) |
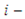 direction and
direction and 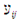 and
and 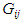 are the Poisson’s ratio and shear moduli in the i-j face, respectively. Equation (2.2) implies anisotropic property of the material only. Materials to be non-homogeneous, different properties of each layer of the shell, we will allow the material property variation in the radial direction as follows:
are the Poisson’s ratio and shear moduli in the i-j face, respectively. Equation (2.2) implies anisotropic property of the material only. Materials to be non-homogeneous, different properties of each layer of the shell, we will allow the material property variation in the radial direction as follows: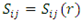 | (2.4) |
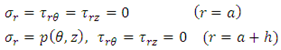 | (2.5) |
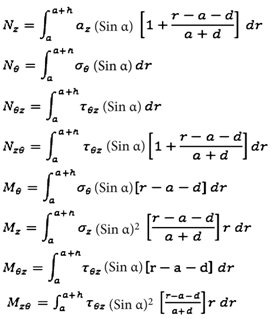 | (2.7) |
3. Formulation of a Boundary Layer Theory
- As explained in the introduction, a theory of shells is distinguished from the exact three dimensional elasticity formulation by the fact that one of the coordinates is suppressed by the mathematical description. The procedure used here for obtaining the two dimensional thin shell equations is that of the asymptotic integration of the (2.1) and (2.2) describing the cylindrical shell. As a first step for integrating (2.1) and (2.2), we non-dimensionalize the coordinates as follows:
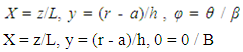 | (3.1) |
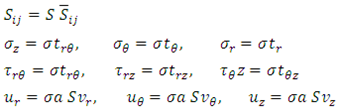 | (3.2) |
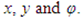 These variables, together with their derivatives with respect to
These variables, together with their derivatives with respect to 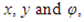 are assumed to be of order unity. The parameters
are assumed to be of order unity. The parameters 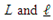 introduced in (3.1) are thus seen to be characteristic length scales for changes of the stresses and displacements in the axial and circumferential directions, respectively.Consider a small parameter
introduced in (3.1) are thus seen to be characteristic length scales for changes of the stresses and displacements in the axial and circumferential directions, respectively.Consider a small parameter 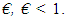 With respect to an arbitrary domain D of the cylinder, M1 is said to be of order
With respect to an arbitrary domain D of the cylinder, M1 is said to be of order 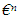 relative to a second quantity M2.
relative to a second quantity M2. 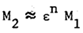 | (3.3) |
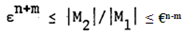 | (3.4) |
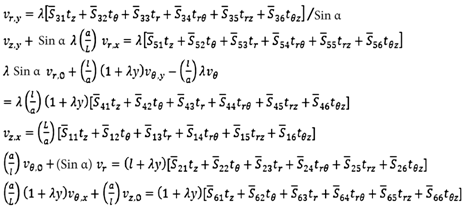 | (3.5) |
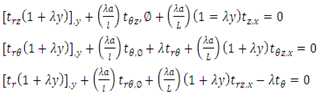 | (3.6) |
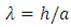 | (3.7) |
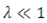 | (3.8) |
 | (3.9) |
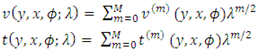 | (3.10) |
4. Shell Theory of Longitudinal and Circumferential Length Scales (Lh)1/2
- We will now develop a theory of both characteristic length scales same as (Lh)1/2, as follows
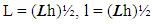 | (4.1) |
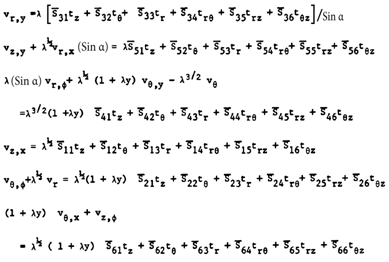 | (4.2) |
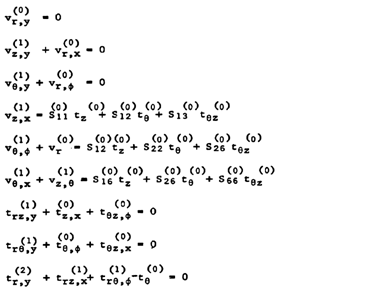 | (4.3) |
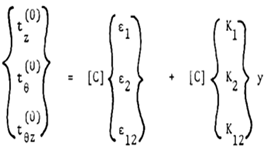 | (4.4) |
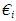 and curvature components ki defined at y = 0, surface for a conical shell are given as follows:
and curvature components ki defined at y = 0, surface for a conical shell are given as follows: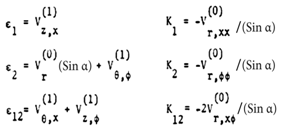 | (4.5) |
 | (4.6) |
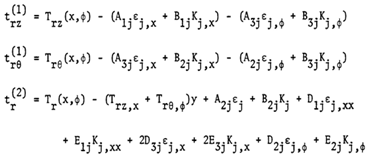 | (4.7) |
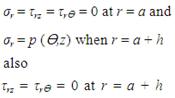 | (4.8) |
5. Application
- We assume here that the contact between layers is such that the strains are a continuous function in thickness coordinate. As the Cij are piecewise continuous functions, the in-plane stresses are also continuous. We would expect the in-plane stresses to be discontinuous at the juncture of layers of dissimilar materials. The transverse stresses are continuous functions of the thickness coordinate. We assume here that the contact between layers is such that the strains are a continuous function in thickness coordinate. As the Cij are piecewise continuous functions, the in-plane stresses are also continuous. We would expect the in-plane stresses to be discontinuous at the juncture of layers of dissimilar materials. The transverse stresses are continuous functions of the thickness coordinate.Although, as mentioned above, the theory developed can consider. Random layering, numerical results are to be carried out for a four-layer symmetric angle ply configuration. For this configuration the angle of elastic axes
 is oriented at
is oriented at  with the shell axis and the layers are of equal thickness.The cone is taken to be clamped at both ends but free to rotate and extend axially at one end. We now choose it to be such that there exists no coupling between Nz and Kz and Mz and €id. As the loading applied is axisymmetric, all the stresses and strains are also taken to be axisymmetric. Numerical calculations are now carried out for a shell of the following dimensions:We will then obtain λ= 0.025 (0.1 / 4.0). Each of the layers is taken to be 0.025 inches thick and thus the dimensionless distances from the bottom of the first layer are given by
with the shell axis and the layers are of equal thickness.The cone is taken to be clamped at both ends but free to rotate and extend axially at one end. We now choose it to be such that there exists no coupling between Nz and Kz and Mz and €id. As the loading applied is axisymmetric, all the stresses and strains are also taken to be axisymmetric. Numerical calculations are now carried out for a shell of the following dimensions:We will then obtain λ= 0.025 (0.1 / 4.0). Each of the layers is taken to be 0.025 inches thick and thus the dimensionless distances from the bottom of the first layer are given by Each layer of the symmetric angle ply configuration (elastic symmetry axes y are oriented at
Each layer of the symmetric angle ply configuration (elastic symmetry axes y are oriented at  is taken to be orthotropic with engineering elastic coefficients of Apollo 38-750 Graphite Fiber as follows:E1 = 300 GpaE2 = 260 GpaG12 = 52 GpaHere, direction 1 signifies the direction parallel to the fibers, while 2 is the transverse direction. Angles chosen were
is taken to be orthotropic with engineering elastic coefficients of Apollo 38-750 Graphite Fiber as follows:E1 = 300 GpaE2 = 260 GpaG12 = 52 GpaHere, direction 1 signifies the direction parallel to the fibers, while 2 is the transverse direction. Angles chosen were  = 0, 15, 30, 45 and 60. Use of the transformation equations (2.7) then yields the mechanical properties for the different symmetric angle ply configurations.Shown in Fig. 3 is the variation of the dimensionless radial displacement with the actual distance along the axis for the different ply angles. The reference surface for the chosen configuration is given by d/h = ½. The integration constants are determined from the edge conditions. The radial deformations of the length scales (Lh)1/2 is shown in Fig. 1 and 2. One will notice the radial deformation rapidly increases along the length scale near the edge while further inside deformations show little change. This area is the so-called edge effect zone or boundary layer; the American Petroleum institute adopted similar theories for its cylindrical shell gas storage tank design (API 650). Locating the edge effect zone can simplifies the calculation of circumferential and longitudinal stiffeners as shown in the References [8] through [11], in relation to the buckling problems, Reference [15].
= 0, 15, 30, 45 and 60. Use of the transformation equations (2.7) then yields the mechanical properties for the different symmetric angle ply configurations.Shown in Fig. 3 is the variation of the dimensionless radial displacement with the actual distance along the axis for the different ply angles. The reference surface for the chosen configuration is given by d/h = ½. The integration constants are determined from the edge conditions. The radial deformations of the length scales (Lh)1/2 is shown in Fig. 1 and 2. One will notice the radial deformation rapidly increases along the length scale near the edge while further inside deformations show little change. This area is the so-called edge effect zone or boundary layer; the American Petroleum institute adopted similar theories for its cylindrical shell gas storage tank design (API 650). Locating the edge effect zone can simplifies the calculation of circumferential and longitudinal stiffeners as shown in the References [8] through [11], in relation to the buckling problems, Reference [15].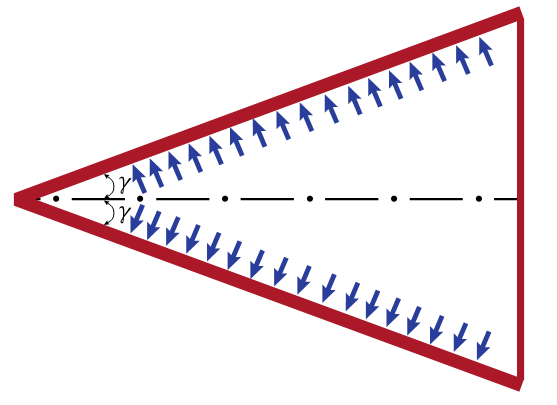 | Figure (3). Conical Shell under Internal Pressure |
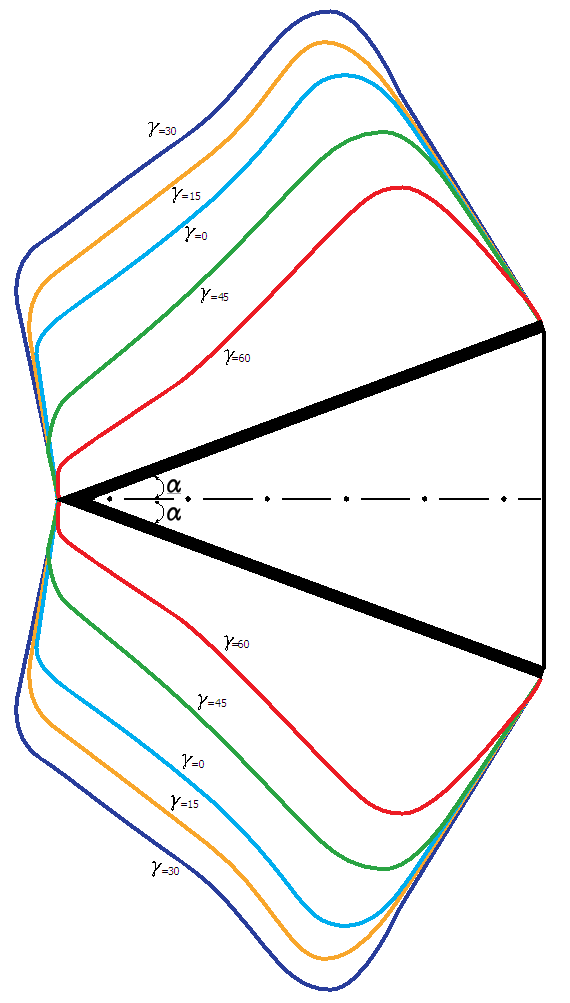 | Figure (4). Axi-Symmetric Deformations |
 = 30 degrees while the minimum displacement is at
= 30 degrees while the minimum displacement is at  = 60 degrees.In each case, the displacements increase in
= 60 degrees.In each case, the displacements increase in  up to
up to 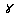 =30 degrees, and thereafter will decrease. Weak and smooth edge effects are the case for large cross-ply angles.
=30 degrees, and thereafter will decrease. Weak and smooth edge effects are the case for large cross-ply angles.6. Conclusions
- In this paper, we first discuss how the approximation shell theories are derived by use of the method of asymptotic integration of the exact three-dimensional elasticity equations for a hybrid anisotropic conical shell.The analysis remains valid for materials, which are non-homogeneous to the extent that their properties are allowed to vary with the thickness coordinate.As a result of the application of this method, one can obtain shell approximate theory of various orders in a systematic manner. The first approximation theories derived in this paper represent the simplest possible shell theories for the corresponding length scales considered. Although 21 elastic coefficients are present in the original formulation of the problem, only six appear in the first approximation theories. The shell theories thus assume the existence of a plane of elastic symmetry. It was seen that various shell theories are obtained by using different combinations of the length scales introduced in the non-dimensionalization of the coordinates and that each theory possesses unique properties such as the orders of stress magnitudes, displacement components and edge effect penetration. In this research, we considered a theory with length scales of (Lh)1/2 for both longitudinal and circumferential directions, where L the actual cone length and h is the total thickness of the cone.To illustrate the use of these theories, the application to layered shells was shown. The results of the analysis showed the radial displacement first increases with increase of the angle between the axis of elastic symmetry and longitudinal shell axis, being largest at 30 degrees. The theory of axial and circumferential length scale of (Lh)1/2 show as a significant edge effect exists and that the penetration of the edge effect changes with the angle in similar fashion as for the radial displacement, being deepest at 30 degrees.
ACKNOWLEGEMENTS
- The research was partially sponsored by Summit Partners in Menlo Park, California, USA.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML