-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Composite Materials
p-ISSN: 2166-479X e-ISSN: 2166-4919
2018; 8(3): 47-56
doi:10.5923/j.cmaterials.20180803.01

Details of Semi-Membrane Shell Theory of Hybrid Anisotropic Materials
1School of Architecture, University of Utah, Salt Lake City, USA
2Department of Architecture, Yeung Nam University, Tae Gu, Korea
Correspondence to: S. W. Chung, School of Architecture, University of Utah, Salt Lake City, USA.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

A new version of partial differential equations and prescribed boundary conditions of already formulated semi-membrane shell theory of anisotropic materials is presented. It is based on the theories been developed by authors previously. The isotropic versions of the theory has been known to be developed nearly a century ago by Vlasov and it has been efficiently utilized for design and analysis. The aerospace vehicle structures and outer space rocket fuel storage tanks designed efficiently however not much for composite materials, while most of recent structural materials are of the combination of anisotropic materials. The semi-membrane cylindrical shell theories are classified as that of very long effective length scale and we adopted here the longest possible longitudinal and short circumferential length scales, respectively, for the formulation. The edge effects due to the prescribed boundary condition penetrate differently depending on material orientation of each layer but all within the limit of length scale (ah)1/2 where Donnell-Vlasov bending theory is valid. Demonstrated that beyond the limit of edge effective zone, membrane or pseudo-membrane state dominates, it is traditionally named semi-membrane state. New simplified governing equations of semi-membrane theory of cylindrical shell are formulated and the physical interpretation of the theory is described.
Keywords: Semi-membrane theory, Pseudo-membrane theory, Donnel-Vlasov theory, Edge effect
Cite this paper: S. W. Chung, G. S. Ju, Details of Semi-Membrane Shell Theory of Hybrid Anisotropic Materials, International Journal of Composite Materials, Vol. 8 No. 3, 2018, pp. 47-56. doi: 10.5923/j.cmaterials.20180803.01.
1. Introduction
- Shell structures have numerous shapes such as cylindrical, spherical and conical configurations.Cylindrical shells are efficiently used for space shuttles, rocket fuel storage tanks, aircraft fuselages, above ground fuel storage tanks and deep water submarines. The advantages of cylindrical shells are not only its functional capacity and aerodynamic features but also a simple coordinate system for the mechanical analysis compared to spherical or conical shapes. For a shell of general shape we will first accept and use the classical assumption of Love then compare our theory with more elaborate theories of Reissner and Donnell-Vlasov as shown in the References [1], [2] and [3]. It is known that Vlasov during the course of simplifying his cylindrical shell equation named Donnell-Vlasov theory he had noticed a proper equation for long longitudinal length, it is interesting that he might have invented the mathematics but never used the terminology “semi-membrane” at all. Who started to name the terminology and how Vlasov was honored are an interesting issue. When analyzing the cylindrical shells, it is common to utilize known physical parameters such as radius (a) thickness (h) and length (L). Donnell, Vlasov and many other scientists classified when develop the analytical model for circular cylindrical shell as following categories: Short and Intermediate effective length, very long effective Length. Figures 4 and 5 indicated the zoning territory but the border line can be altered by the property of material and thickness of lamination.Once we built the analysis for the cylindrical shells we could easily convert to the other shape shells as shown in the References, [7], [8], [9], [10], However, the mathematics to describe its behavior and characteristics are complicated and it is more of challenge when the materials are anisotropic and combination of different anisotropic materials, hybrid anisotropic shell structures. Let us first start with three dimensional coordinate system of shell structures.The system is of longitudinal (X, z), circumferential (φ, θ) and radial (r) as shown in Figure 1 and 2. The original and non-dimensional coordinates as shown in the figures are used to allow an asymptotic integration process. According to the exact three-dimensional theory of elasticity, a shell element is considered as a volume element. All possible stresses and strains are assumed to exist and no simplifying assumptions are allowed in the formulation of the theory. We therefore allow for six stress components, six strain components and three displacements as indicated in the following equation:
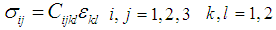 | (1) |
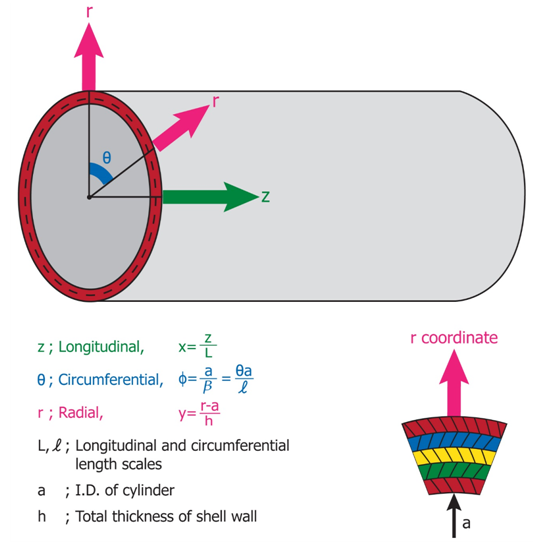 | Figure 1. Coordinates of the Cylindrical Shell |
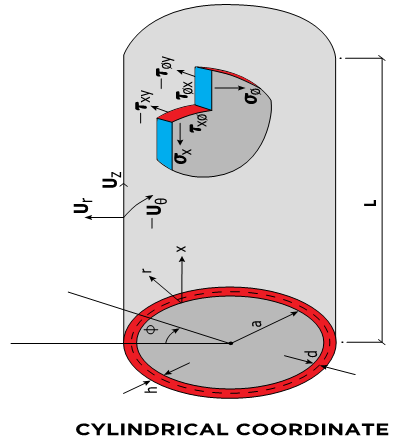 | Figure 2. Normal and Shear Stresses |
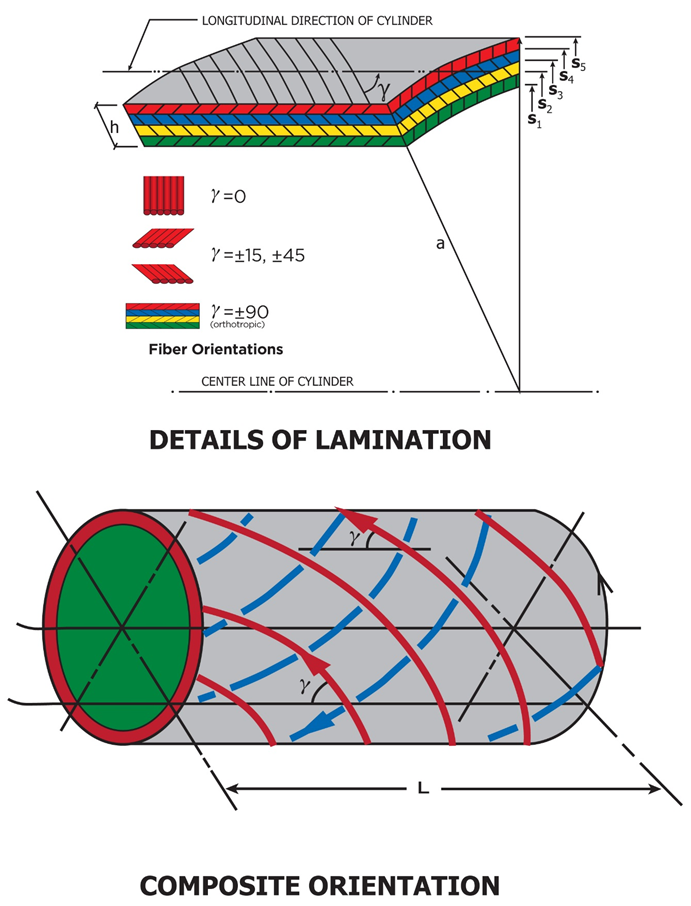 | Figure 3. A Laminated Cylindrical Shell, Material Orientation γ |
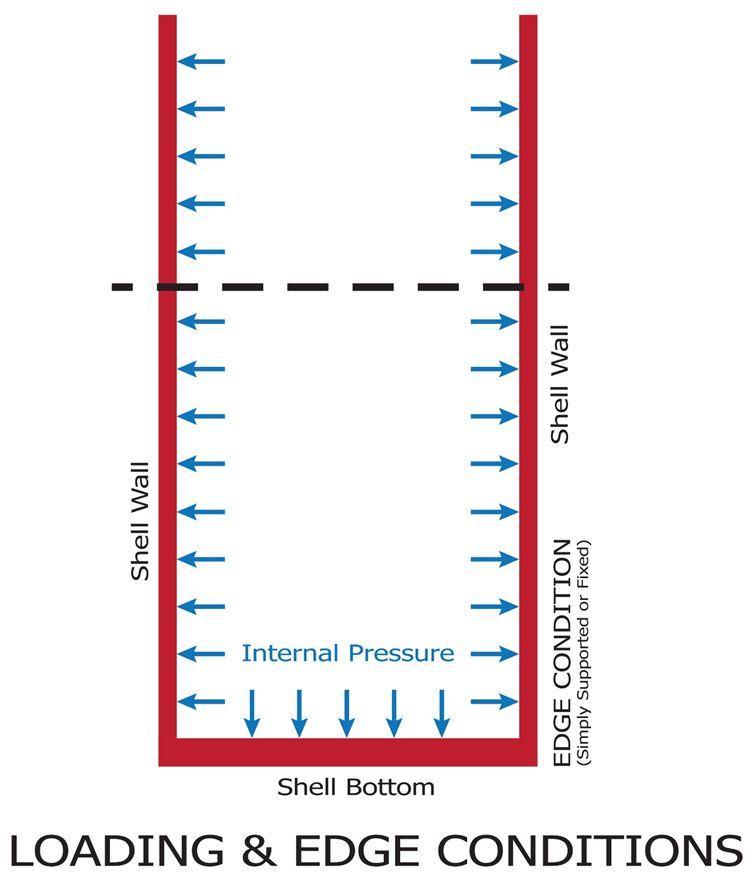 | Figure 4. Cylindrical Shell under Internal Pressure |
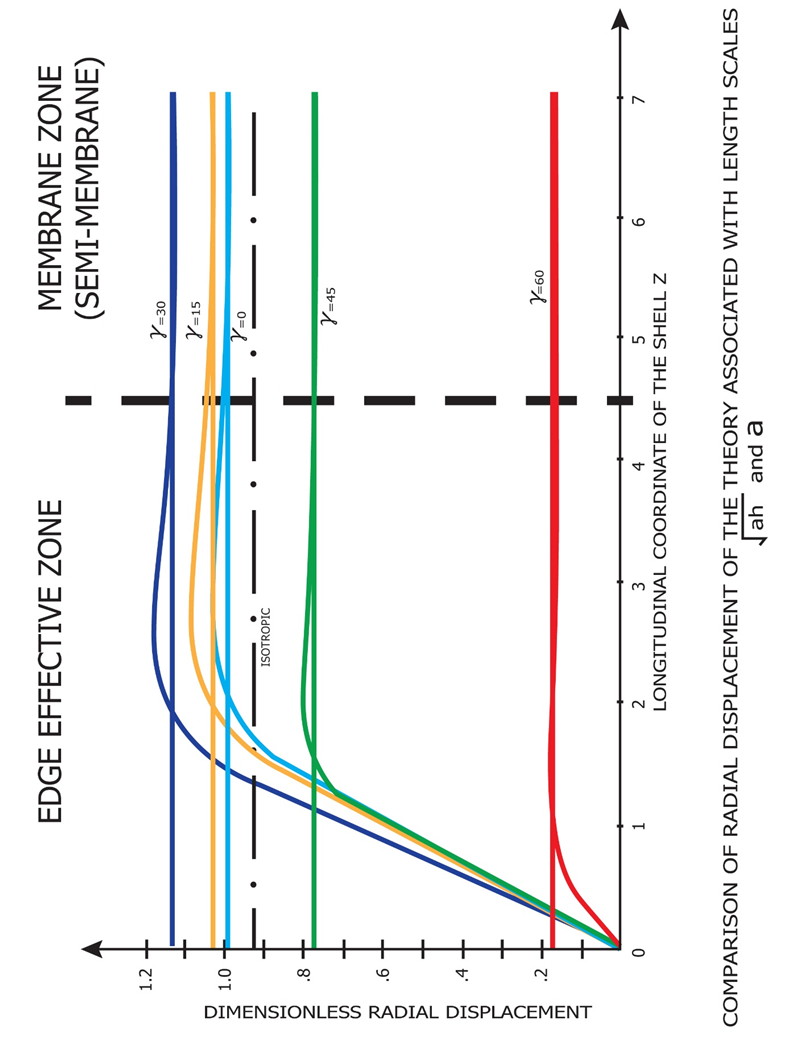 | Figure 5. Edge Effective Zone of Bending and Pure Membrane Theories |
 | (2) |
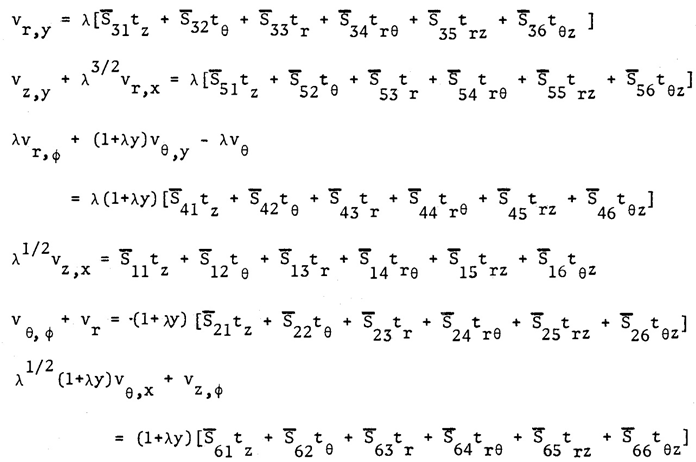 | (3) |
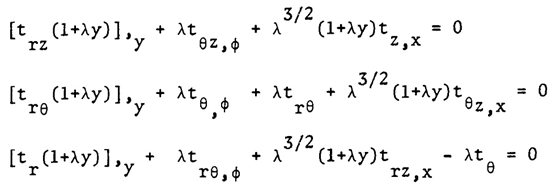 | (4) |
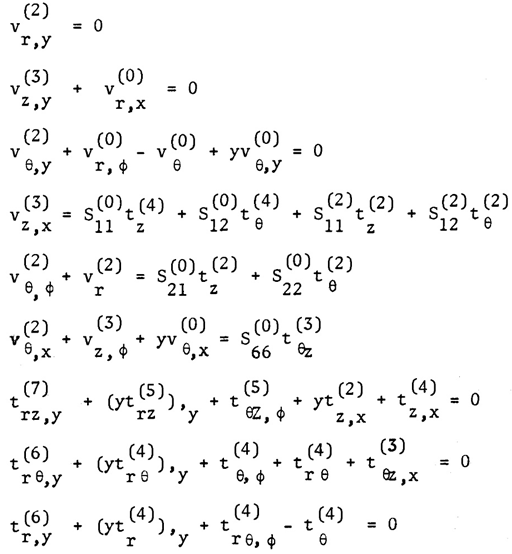 | (5) |
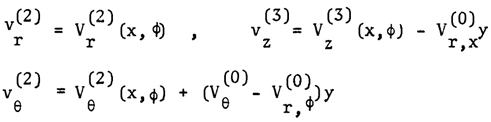 | (6) |
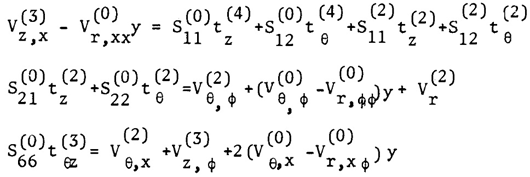 | (7) |
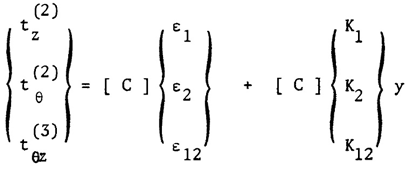 | (8) |
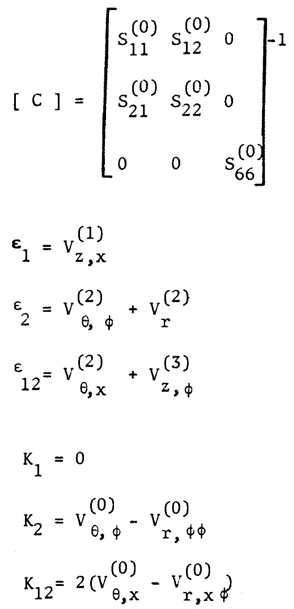 | (9) |
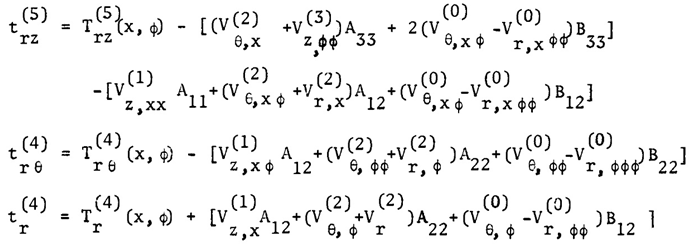 | (10) |
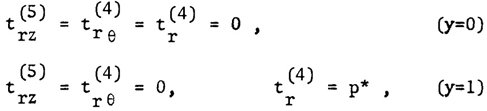 | (11) |
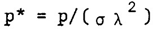 | (12) |
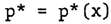 | (13) |
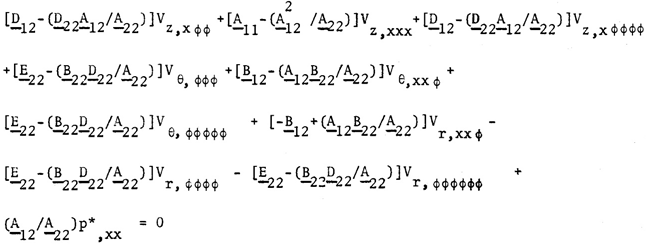 | (14) |
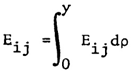 | (15) |
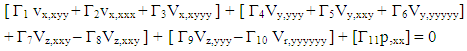 | (16) |
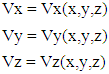 | (17) |
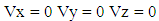 | (18) |
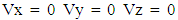 | (19) |
2. Conclusions
- The theory of circular cylindrical shell is developed and formulated by adopting circumferential length scale as inner radius, a, and longitudinal length scale, a(a/h)1/2, which is the longest possible physical length and extended to hybrid anisotropic materials and the governing equations are well compared to classical theories of Vlasov, Calladine and Gould, etc. which are of isotropic material as shown in the references [6], [10] and [11] respectively.The adopted the circumferential length scale is equal to the inner radius, a, is membrane state circumferentially as shown in the pseudo membrane theory formulated by Chung and Hong as shown in the reference [19]. Longitudinally, a long length scale was adopted, therefore radial deformation and circumferential stresses are of exponentially decaying patterns as explained by Vlasov, Calladine as shown in the references [7], [8] and [20] respectively.Due to the complexity of hybrid anisotropic material being used, the developed theory is of higher order partial differential equations but it should be considerably simplified considering the axi-symmetric nature of load and deformations and very long longitudinal length scale. The equations and formulations used in this article are clarified by the Reference of [22]. The simplification procedure together with prescribed edge conditions further clarified.
ACKNOWLEDGEMENTS
- The research was sponsored by Summit Partners in Menlo Park, California, USA and graciously acknowledged.
List of Symbols
- a : Inside Radius of Cylindrical Shellh : Total Thickness of the Shell WallSi : Radius of Each Layer of Wall (i = 1, 2, 3 --- to the number of layer)L : Longitudinal Length Scale to be defined, Also Actual Length of the Cylindrical Shell Ei : Young’s Moduli in i DirectionGij : Shear Moduli in i-j FaceSij : Compliance Matrix of Materials of Each Layerr : Radial Coordinatel : Circumferential Length Scale to be defined Ɣ : Angle of Fiber Orientationσ : Normal Stressesε : Normal Strains z, θ, r : Generalized Coordinates in Longitudinal, Circumferential and Radial Directions Respectivelyτ : Shear Stressesεij : Shear Strains in i-j Faceλ : Shell Thickness / Inside Radius (h/a)Cij : Elastic Moduli in General X, φ, Y : Non Dimensional Coordinate System in Longitudinal, Circumferential and Radial Directions Respectively Γ : Constants used for partial differential equations
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML