1. Introduction

Aluminum is one of the major materials used in modern mechanical engineering [1]. Its main merits (the small specific weight and high plasticity) are successfully combined with the uncommon durability as well as with the high heat and corrosion resistances by means of introduction of various impurities. Aluminum is applied both in the form of alloys with other elements [2, 3], and as a part of intermetallides [4, 5]. Its use as binding material for creation of composites on the basis of oxides, carbides, nitrides and borides of various elements, and of carbon fibers is known [6, 7].

Alloys and compounds of the Al-Ti system having the small specific weight, high durability and elasticity are widely used in the aviation (Figure 1) and space industry, and also in shipbuilding [8]. At the same time, it is known that these alloys often contain C and N impurities [9, 10]. Influence of the titanium nitride and carbide on formation of titanium carbonitride-tungsten-aluminium alloys is described in [7]; and effect of C and N impurities in phase transitions in the Al-Ti system is considered in [10]. However their direct influence on mechanical properties of aluminium remains not studied. Also properties of aluminium containing nanoparticles of the titanium nitride and carbide which in itself possess the high hardness and fragility remain unaddressed.

Figure 1. The Russian modern airplane Superjet 100

Our work is attempt to find out, whether it is possible to use the Al-TiC and Al-TiN composites for creation the material similar to hard alloys where transitional metals are used as binders [11, 12].

2. Methods and Technique

When developing new nanostructural materials and devices, the increasing role starts playing the computer modeling urged to predict not only their structure, but also properties. It is known that most adequately such modeling is carried out by means of quantum-mechanical methods, the most powerful and reliable from which is the density functional theory (DFT) [13], or to be exact today its version offered by Kohn and Sham (KS) [14].

The KS approach declares that one-particle electron energies ε_i and wave functions ψ_i may be found from a set of equations

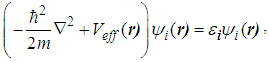(1)

where

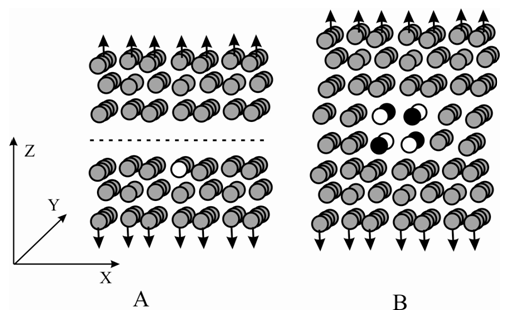
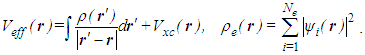The exchange correlation potential V_xc(r) may be calculated in some known approximations. There are many program realizations of the KS method: spin restricted, spin polarizes, full electron, pseudopotential, and so on. In this work we used the FHI96md package [15] based on using of pseudopotentials [16]. It means that the calculations took into account only the valence electrons. This approach was previously used with advantage for many systems, including transition metal compositions [17-20]. In all cases, the generalized gradient approximation [21] to description of the exchange-correlation interactions has been chosen and the optimization of the atomic geometry has been performed.

All pseudopotentials were constructed with the FHI98PP package [22]. They were checked for the absent of the so-called 'ghost' states. The energy cutoff for the pane wave set was equal to 40 Ry and the special k-point (0.25; 0.25; 0.25) was used.

The Al-TiC and Al-TiN composites were modeled as crystalline slabs consisted of Al atoms and embedded nanoparticles of TiC or TiN. The border between grains of pure Al was presented as a contact of two crystalline slabs.

The slabs were described as infinite in directions X and Y by use of the periodical border conditions, while they had finite sizes in the direction of Z. General schemes of modeling systems are presented in Figure 2.

Figure 2. Atomic schemes used in this work for study of durability. A) Aluminum, undoped and doped. White circle represents an atom of impurity (Ti, C, N). B) Aluminum with an embedded nanoparticle (TiC or TiN): black circles are Ti atoms; white circles are C or N atoms; gray circles are Al atoms

In order to test our approach we calculated the surface energy of pure aluminum and have obtained the value of 1.2 J/m². Published values of the surface energy of aluminum [23] lie in the interval of 0.9-1.5 J/m²; thus our approach is rather good.

We applied the following technique to research of durability. The systems which are schematically represented in Figure 2 were initially optimized. That is, for each system an atomic configuration corresponding to a minimum of a total energy was wound. After that the top and lower atoms of system (marked in Figure 2 with shooters) were step by step displaced in the direction of Z, and fixed on each step. Other atoms of system had opportunity to be displaced under the influence of interatomic forces, and in system there was a balance again. Thus, the distance between outer sides of slabs increased, and the total energy of system changed. We found the variations of the total energy ΔE as functions of elongation ΔZ, and then the applied strength P was calculated according the formula

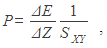where S_XY is the system square in the XY plane.

3. Results and Discussions

First of all, we investigated durability of pure aluminum. That is, we found change of the total energy of the system at increase in distance between outer surfaces of the slabs, and calculated the arising tension. The result is presented in Figure 3 (the curve “Al pure”). We see that strength of pure aluminum is close to 5.5 GPa, and the critical length of stretching with which there comes destruction of the material is equal to 4 percent. The tensile strength received by us many times over exceeds the values observed for real aluminum materials (0.1-0.5 GPa depending on type of the alloy) [24]. It no wonder as in real material there is a set of the factors reducing durability. Besides, the nanoscale size of the studied system gives contribution to increasing of durability. In [19] the similar overestimate of strength was received for tungsten carbide nanoparticles.

Then we studied influence of TiC and TiN. The analysis of Figure 3 shows that their influence on the aluminum durability (more precisely, on durability of a composite material on the basis of aluminum) is ambiguous. Presence of the titanium carbide particles increases durability, but it practically does not influence plasticity. Titanium nitride reduces both durability, and the lengthening limit.

For comparison we studied influence of single atomic impurities (Ti, C, N) in aluminum. Results are presented in Figure 3 and in Table 1. We see that titanium increases the tensile strength and the lengthening limit in accordance with the known data [1, 3, 25-27]. The atomic carbon or nitrogen also increase the tensile strength and the lengthening limit work; and their do it approximately by the same way. However the TiC and TiN nanoparticles influence on mechanical properties of aluminum by different ways. The TiC particle increases the tensile strength (to 6.4 GPA) and keeps the plasticity of aluminum, while TiN particle decreases both the tensile strength (to 4.0 GPA) and the lengthening limit (to 4 percent).

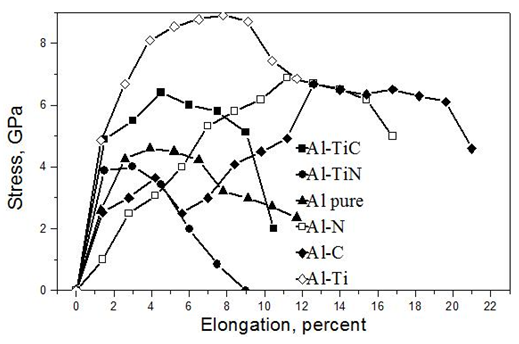Figure 3. Dependence of stress on elongation in the studied systems

Table 1. Values of the tensile strength P and the lengthening limit L in the studied systems of aluminum

Unfortunately there are no experimental data on mechanical properties of Al-C, Al-N, Al-TiC, and Al-TiN systems, thus we can be compared with our results, thus, we can compare our results only between themselves.

4. Conclusions

Quantum-mechanical modeling of composites on the basis of aluminum allows to make a conclusion that the single impurities Ti, C, N influence the aluminum durability better than nanoparticles of TiC or TiN do. Presence of particles of the titanium carbide increases durability, but practically does not influence plasticity. The titanium nitride reduces both durability, and lengthening limit.

ACKNOWLEDGEMENTS

This work is supported by a grant of the Russian Research Foundation “Development of program and hardware for the system of intellectual diagnostics of vehicles and constructions in the Arctic conditions at the remote access”.