-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Composite Materials
p-ISSN: 2166-479X e-ISSN: 2166-4919
2017; 7(3): 82-102
doi:10.5923/j.cmaterials.20170703.02

A Comparative Analytical, Numerical and Experimental Analysis of the Microscopic Permeability of Fiber Bundles in Composite Materials
M. Karaki1, A. Hallal2, R. Younes3, F. Trochu4, P. Lafon1, A. Hayek3, A. Kobeissy3, A. Fayad3
1Laboratoire des Systèmes Mécaniques et d'Ingénierie Simultanée (LASMIS), Université de Technologie de Troyes, Troyes Cedex, France
2SDM research group, Department of mechanical Engineering, school of Engineering, Lebanese International University, Beirut, Lebanon
3Faculty of Engineering, Lebanese University, Rafic Hariri campus, Beirut, Lebanon
4Chair on Composites of High Performance, école polytechnique de Montréal, Canada
Correspondence to: M. Karaki, Laboratoire des Systèmes Mécaniques et d'Ingénierie Simultanée (LASMIS), Université de Technologie de Troyes, Troyes Cedex, France.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this comparative study, convenient analytical models evaluating the permeability of unidirectional fibrous media towards normal and parallel flow are selected. These models are compared with respect to available data early published. Static and transient mode simulations are launched in order to filter out the consistent bibliography values; analytical models are later compared with respect to the selected data.The analysis of the comparative study presents that Bahrami and Tamayol, Drummond and Tahir, Berdichevsky and Cai ISCM, and unified (square) models have good agreement with these data for longitudinal microscopic permeability components. Concerning transverse microscopic permeability, Berdichevsky and Cai ISCM (hexagonal), Gebart (hexagonal), Drummond and Tahir (hexagonal), and Kuwabara models are elected to be the most accurate models.
Keywords: Microscopic permeability, Analytical, Numerical, Experiment
Cite this paper: M. Karaki, A. Hallal, R. Younes, F. Trochu, P. Lafon, A. Hayek, A. Kobeissy, A. Fayad, A Comparative Analytical, Numerical and Experimental Analysis of the Microscopic Permeability of Fiber Bundles in Composite Materials, International Journal of Composite Materials, Vol. 7 No. 3, 2017, pp. 82-102. doi: 10.5923/j.cmaterials.20170703.02.
Article Outline
1. Introduction
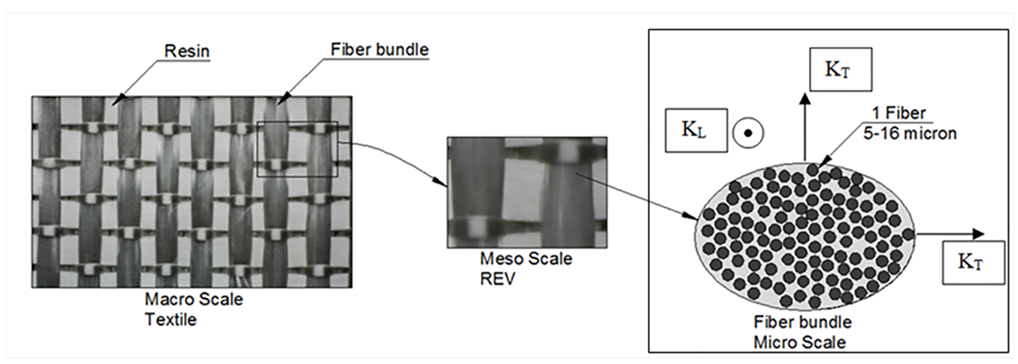
- Liquid composite molding (LCM) is one of the most popular composite manufacturing processes due to its repeatability, medium costs, and flexibility. Resin is injected or infused into a mold filled with dry fabric, this process is performed under different conditions (constant pressure or velocity, atmospheric or vacuum outlet ports…) with different methods such as RTM, VARTM, VARI, and RIFT.In order to simulate the resin injection and to predict the filling time of any structure, the permeability of the fabric is required. A dry fabric is considered as a dual scale medium, Figure 1. Researchers classify the flow inside the bundles as “microscopic flow”, between the bundles as “mesoscopic flow”, and as “macroscopic flow” at piece level. In other words, the permeability of bundles or unidirectional yarns is called microscopic permeability while that for a fabric is called macroscopic permeability. Microscopic permeability is an important parameter to discover resin flow through the fiber bed and understand the mechanisms of air entrapment which governs the quality of composite parts made by LCM. Moreover, it is an essential step towards macroscopic permeability modeling.
 | Figure 1. P3W-GE044 from 3TEX Company |
1.1. Problem Statement
- This study deals with microscopic permeability of unidirectional yarns; longitudinal permeability KL and transverse permeability KT. In general, the evaluation of these permeability values is done by experimental measurements, analytical models, or finite Element (FE) numerical simulations. While analyzing the previously stated prediction methods, wide scattering is observed. In addition, many analytical models exist, while there is no clear comparative study that evaluates all these models.The main objective of this paper is to evaluate the available analytical models, by comparing their results to the available bibliography data. However, because of the wide scattering found in bibliography results, this data is to be refined. Thus a finite element modeling is done, in which a more realistic unit cell is used where the fibers are arranged in a random manner; neither square nor hexagonal. Static mode and transient mode simulations are launched. The values of transient simulations approved the consistency of static mode simulations. The bibliography results that better fit the FE modeling results are selected. Then a comparative study is performed and the best analytical models for KL and KT are presented.
1.1.1. Bibliographic Experimental and Numerical Scattering
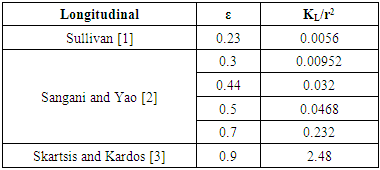
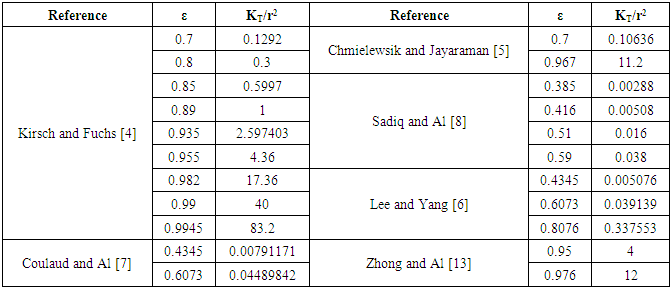
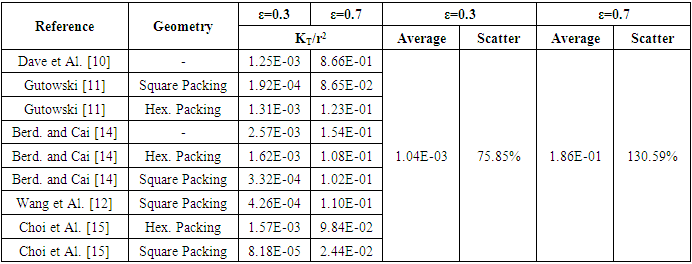
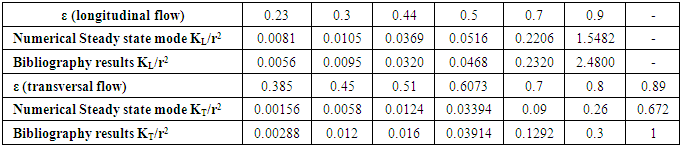
- Researchers [1-12] predicted the permeability values either by numerical simulations or experimental measurements. This section aims to show the scattering found for both experimental measurements and numerical predictions for aligned fiber beds with the same fiber volume fraction. Permeability measurements depend on many parameters including the method, the apparatus, the techniques and operator skills, as well as the injection method which could be either radial or unidirectional. On the other hand, numerical simulations depend on many parameters such as the used code, the used method, the boundary conditions, and the most important and influencing parameter which is the unit cell selection. Table 1, Table 2, and Table 3 show different experimental measurements and numerical simulations of the dimensionless permeability components KL/r2 and KT/r2 values, where “r” is the fiber radius.
|
|
|
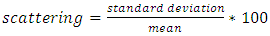 | (1) |
|
1.1.2. Analytical Scattering
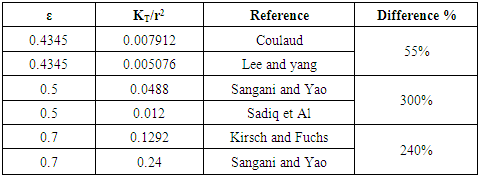
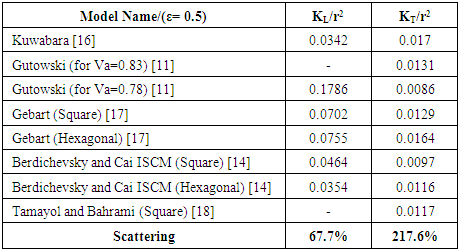
- Analytically, researchers have studied the microscopic permeability for unidirectional fibers, and then derived various analytical models based on 4 different modeling approaches:• Lubrication approach• Capillary approach• Analytic Cell modeling• Mixed models based on previous models.Table 5 shows a comparison between some analytical models from the bibliography on a selected fiber volume fraction (ε = 0.5). It’s well noticed that for the same fiber volume fraction, different models give rise to values of permeability with a scatter more than 60% for longitudinal permeability and more than 200% for transversal permeability models.
|
1.2. Objectives
- The main objective of this work is to select the best available analytical models predicting the permeability values for unidirectional fiber beds. To do so, seven analytical models predicting the longitudinal microscopic permeability [9, 11, 14, 16, 17, 23, 24] and seventeen models [6, 9, 11, 14, 16, 17, 20-23, 25-27] predicting the transversal microscopic permeability are selected from bibliography. From the comparison, the best models for predicting microscopic longitudinal and transversal permeability are selected.
1.3. Methodology
- Reviewed analytical models’ calculations are compared with numerical simulations or experimental results from bibliography; but these results showed big differences between each other for the same fiber volume fraction as previously explained in the first part. This reveals the importance of performing a new numerical study simulating a real experiment and eliminating experiment’s problems.Figure 2 shows two different fabrics which are 3D Orthogonal from 3TEX with fiber volume fraction equal to 55.76%, and a unidirectional stitched fabric (U14EU920) from SAERTEX with fiber volume fraction equal to 60.59%. Note that these real injections are done in order to affirm that the fiber arrangement is random. Thus the numerical FE modeling is performed based on a random fiber packing structure. This study measures averaged volume filling speed under a constant pressure. In other words, it is the saturated permeability value. The study is done in both longitudinal and transversal directions. A more advanced study is done for the same unit cell in a transient mode; where the flow front position is detected as function of time, taking into consideration capillary effect. Averaged unsaturated permeability is deduced. This simulation approved the consistency of static mode simulation.
 | Figure 2. Two fabrics: 3D Orthogonal from 3TEX at a fiber volume fraction equal to 55.76% and unidirectional stitched fabric (U14EU920) from SAERTEX at a fiber volume fraction equal to 60.59% |
1.4. Organization
- A review of the available analytical models in the literature is established. In the second section, a numerical study is launched in order to simulate the longitudinal and transversal flow in aligned fiber beds at different fiber volume fractions in a steady state mode “saturated permeability”. In the third section, the experiments are selected based on the numerical simulations and a comparative study is launched in order to select the best analytical models based on the previous numerical simulations and selected experiments. Then, a numerical simulation in a transient free boundary problem mode is done and consequently the best analytical models will be filtered from the selection made in the third part. At the end of this study, a conclusion is deduced.
2. Analytical Models
- Studies on the permeability of fibrous media date back to the experimental work of Carman [28] and Sullivan [1] in 1940s, and theoretical analyses of Kuwabara [16], Happel [23] and Brenner [29]. (Appendix 1 Eq.1). Kuwabara [16], solving vorticity transport and stream function equations and employing limited boundary layer approach, predicted the permeability of flow normal to randomly arranged fibers for materials with high porosities. (Appendix 1 Eq.2,3). Happel [23] and Brenner [29] analytically solved the Stokes equation for parallel and normal flow for a single cylinder with free surface model (limited boundary layer). The boundary conditions used by Happel and Brenner [29] were different from Kuwabara’s study [16]. They hypothesized that the flow resistance of a random 3D fibrous structure is equal to one third of the parallel plus two third of the normal flow resistances of 1D array of cylinders. Later, Sangani and Acrivos [27] performed analytical and numerical studies on viscous permeability of square and staggered arrays of cylinders for the entire range of porosity values, when their axes were perpendicular to the flow direction. Their analytical models were accurate for the lower and higher limits of porosity (Appendix 1 Eq.4).Drummond and Tahir [20] solved Stokes equations for normal and parallel flow towards different ordered structures. They used a distributed singularities method to find the flow-field in square, triangular, hexagonal, and rectangular arrays. They compared their results with numerical values of Sangani and Acrivos [27] for normal flow. The model of Drummond and Tahir [20] for predictting transversal permeability values was very close to those predicted by Sangani and Acrivos model [27], thus, it is accurate only for highly porous materials (Appendix 1 Eq.5,6,7).Sahraoui and Kaviani [26] included inertial effects and they numerically determined the permeability of cylinders for normal flow. They also proposed a correlation which is accurate for a limited range of porosity values, i.e., 0.4 < 0.7 (Appendix 1 Eq.8). A general mathematical model derived by Gutowski [11] assumed that the fibers make up a deformable, nonlinear elastic network. The resin flow is modeled using Darcy’s Law for anisotropic porous medium. (Appendix 1 Eq.9). Gebart [17] derived an analytical model to predict the unidirectional permeability starting from Navier-Stokes equation. (Appendix 1 Eq.10, 11) In 1993, Berdichevsky and Cai [14], after performing some numerical simulations, considered that the permeability depends on the fiber volume fraction and the ultimate fiber volume fraction. Then they derived a unified empirical model. (Appendix 1 Eq.12, 13). Then in the same year, they developed their model “self consistent method model” to “improved self consistent model “[14], where Stokes flow and Darcy flow are then respectively considered at different regions. Boundary and interface conditions as well as two consistency conditions including the total amount of the flow and the energy dissipation, are applied accordingly. The permeability is solved based on these considerations. This improved permeability model captures the flow characteristics in a given fiber bundle. In the transverse flow case, the gaps between neighboring fibers govern the flow resistance. The derived expression for the transverse permeability contains two variables, the averaged fiber volume fraction and the maximum packing efficiency, which adequately describe the status of a fiber bundle. (Appendix 1 Eq.14,15).Phelan and Wise [25] studied the transverse flow through rectangular arrays of porous elliptical cylinders and derived a semi-analytical model based on lubrication theory. The Brinkman equation is used to model the flow inside porous structures, and the Stokes equation to model the flow in the open media between the structures (Appendix 1 Eq.16). Lee and yang [6] considered the flow as a non-Darcy flow through a porous medium. The continuity equation and the momentum equation in pore scale are solved on a Cartesian grid system. To avoid the numerical difficulties resulting from the flow domain of irregular shape, the weighting function scheme along with the APPLE algorithm and the SIS solver are employed. The Darcy-Forchheimer drag (pressure drag) is then determined from the resulting volumetric flow rate under a prescribed pressure drop to derive their permeability model. (Appendix 1 Eq.17). Brushke and Advani [22] considered the flow across regular arrays of cylinders. The analytic solutions are matched to produce a closed form solution. This is done by employing the lubrication approach for low porosities and the analytic cell model solution for high porosities. (Appendix 1 Eq.18). Using numerical simulations, Van der Westhuizen and Du Plessis [24] proposed a correlation for the normal permeability of 1D fibers. (Appendix 1 Eq.19,20). Tamayol and Bahrami [21] performed studies on the ordered fibrous media towards normal and parallel flow, thus the permeability is obtained analytically. To predict permeability, a compact relationship is suggested by modeling 1D touching fibers as a combination of channel-like conduits. Moreover, analytical relationships are developed for pressure drop and permeability of rectangular arrangements. This is performed by using an “integral technique” and simulating a parabolic velocity profile within the unit cells. The experimental results collected by others for square arrangement confirm the data of the developed models. (Appendix 1 Eq.21,22).Tamayol and Bahrami [18] studied the transverse permeability of fibrous porous media both experimentally and theoretically. A scale analysis technique is used in order to obtain the transverse permeability of fibrous media with a variety of fibrous matrices including square, staggered, and hexagonal unidirectional fiber arrangements. In this field, a relation is designated between the permeability and the porosity, fiber diameter, and tortuosity of the medium. Also, the pressure drop in several samples of tube banks of different arrangements and metal foams is measured in the creeping flow regime. The obtained results are then utilized to calculate the permeability of the samples. The developed compact relationships are confirmed by performing comparison with the present experimental results and the data given by others. (Appendix 1 Eq.23,24).The models listed in this section predict the longitudinal and transversal microscopic permeability “KL” and “KT”, for most models the permeability is a function of the fiber radius “r” and the fiber volume fraction “Vf”. However, for some models the permeability is linked to other parameters like the maximum fiber packing factor “Vfmax”, geometrical effects “C, C1…’’, packing structure (hexagonal or square or other structures) “Va”.
3. Numerical Steady State Method and Results (Saturated Permeability)
- In this section, a FE modeling, using COMSOL MULTIPHYSICS software which consists of a CFD analysis is performed to estimate the microscopic saturated permeability value of multiple cases involving porous media. Two cases were studied, which involve a longitudinal and a transversal flow through certain porous media in order to predict the saturated permeability value of the media. A finite element (FE) based model for viscous, incompressible flow through random packing of fibers is employed for predicting the permeability associated in the porous media.
3.1. Methodology
- In this study, random arrangement of fiber is considered, which is shown to be as most representative for a real fiber stacking. Figure 3 shows the 2D unit cell dimensions for transverse permeability predictions having a length of 0.33mm and a width of 0.1mm. However, the 3D unit cell dimensions for longitudinal permeability are length = 0.33mm, width = 0.1mm, and depth=1mm. Different fiber contents are selected to cover a wide range of porosities (0.3 to 0.9) for both transversal and longitudinal simulations Figure 4 and Figure 5. Porosities are selected with respect to available data from the bibliography; refer to the introduction.
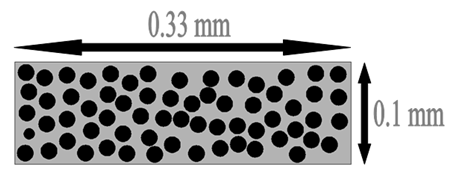 | Figure 3. Unit cell Dimensions |
 | Figure 4. Selected porosities for transversal flow simulation |
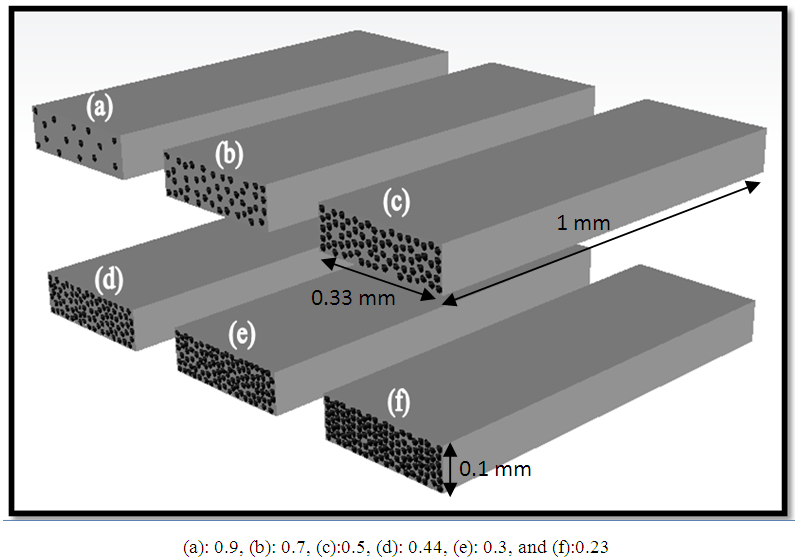 | Figure 5. Selected porosities for transversal flow simulation |
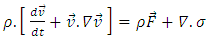 | (2) |
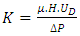 | (3) |
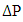 is the pressure drop, K is the permeability tensor of the porous medium,
is the pressure drop, K is the permeability tensor of the porous medium, 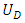 is the velocity of the fluid, and H is the depth of the unit cell.The flow Reynolds number should be kept sufficiently low to ensure negligible effects of inertial terms. Reynolds number equation (4) is ranged between 1 and 10 (1< Re < 10) [31], Where
is the velocity of the fluid, and H is the depth of the unit cell.The flow Reynolds number should be kept sufficiently low to ensure negligible effects of inertial terms. Reynolds number equation (4) is ranged between 1 and 10 (1< Re < 10) [31], Where 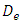 is the equivalent pore diameter.
is the equivalent pore diameter.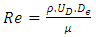 | (4) |
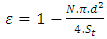 | (5) |
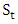 is the total surface of the unit cell. So for a selected fluid “selected viscosity”, on a selected porosity and on a predefined inlet and outlet pressures the filling time is obtained from the simulation. Using equation (3) the saturated permeability is calculated.
is the total surface of the unit cell. So for a selected fluid “selected viscosity”, on a selected porosity and on a predefined inlet and outlet pressures the filling time is obtained from the simulation. Using equation (3) the saturated permeability is calculated.3.1.1. Selected Porosities
- Based on the available data from literature, different porosities were selected Table 6, in order to predict the microscopic permeability values on these porosities.
|
3.1.2. Flow Type and Fluid Properties
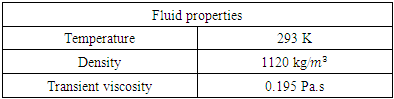
- In fluid transients, laminar flow occurs when a fluid flows in parallel layers, with no disruption between the layers. At low velocities, the fluid tends to flow without lateral mixing, and adjacent layers slide past one another like playing cards. Neither cross-currents perpendicular to the direction of flow, nor eddies or swirls of fluid exist. In laminar flow, the motion of the particles of the fluid is very orderly with all particles moving in straight lines parallel to the walls. The fluid used in simulations is epoxy resin which has the properties shown in Table 7.
|
3.1.3. Meshing Technique
- CFD simulation requires that the computational domain gets divided into small cells where the flow is modeled and the flow equations are solved. COMSOL MULTIPHYSICS software is used to generate the mesh that will be used in simulations involving random form. The generated mesh for longitudinal and transversal unit cells and meshing controls are shown respectively in Figure 6 and Table 8. For example for a longitudinal permeability unit cell for a Vf of 0.5, the complete mesh consists of 1603619 domain elements, 461336 boundary elements, and 57153 edge elements.

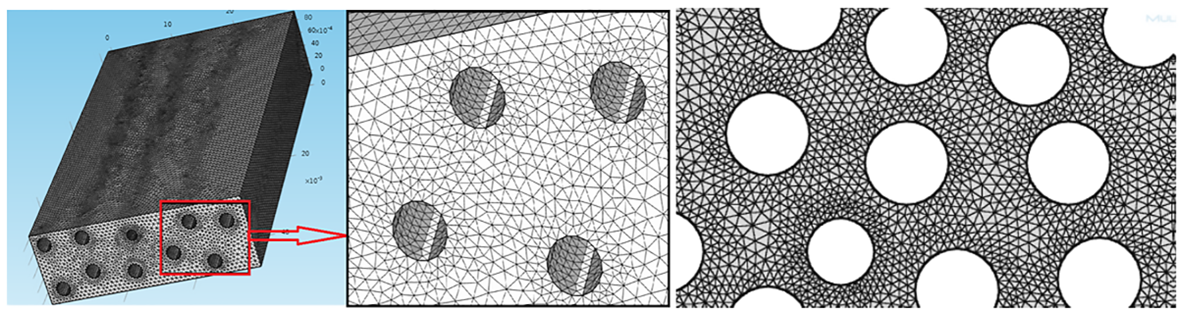 | Figure 6. Generated mesh for longitudinal and transversal unit cells |
|
3.1.4. Boundary Conditions
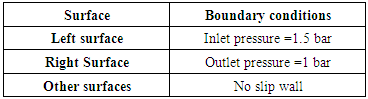
- After the mesh process is completed, the next step is to specify the boundary conditions. Similar boundary conditions were used in all the simulations, which are shown in Table 9. Type of boundary condition: constant pressure with no viscous stress.
|
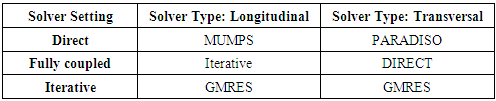
3.1.5. Solver Settings
- Since the flow in the simulations that were performed is supposed to be Laminar (low velocity flow), the Laminar model that solves the Navier-Stokes equations was used Table 10.
|
3.2. Results and Comparison for Numerical Simulations in Steady State Mode
- The results of the calculated permeability values are shown in the Table 11. In the next section, two comparative studies are launched for both longitudinal and transversal microscopic permeability values; where in the results derived from numerical steady state mode simulations and experimental measured results will be compared with results derived from available analytical models.
|
3.2.1. Comparison for Longitudinal Flow (Steady State mode)
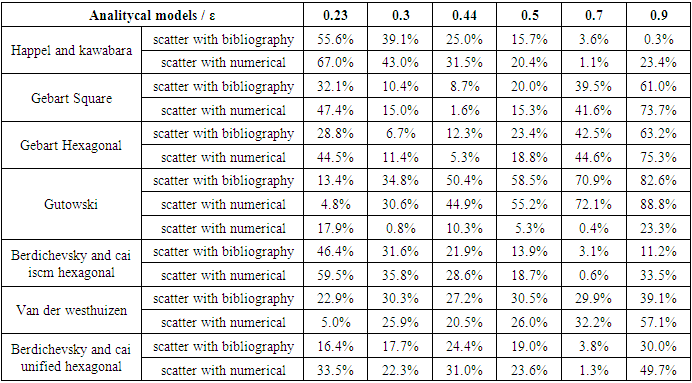
- As shown in Table 12 and Chart 1, Gutowski model values compared with the bibliography results show big scatter at most of the selected porosities such as 34.8% at porosity ε = 0.3, and keeps rising till 70.9% at porosity ε = 0.7. Similarly, the comparison of these models’ values with the simulation reveals almost same scattering ranging between 30.6% and 72.1%.
|
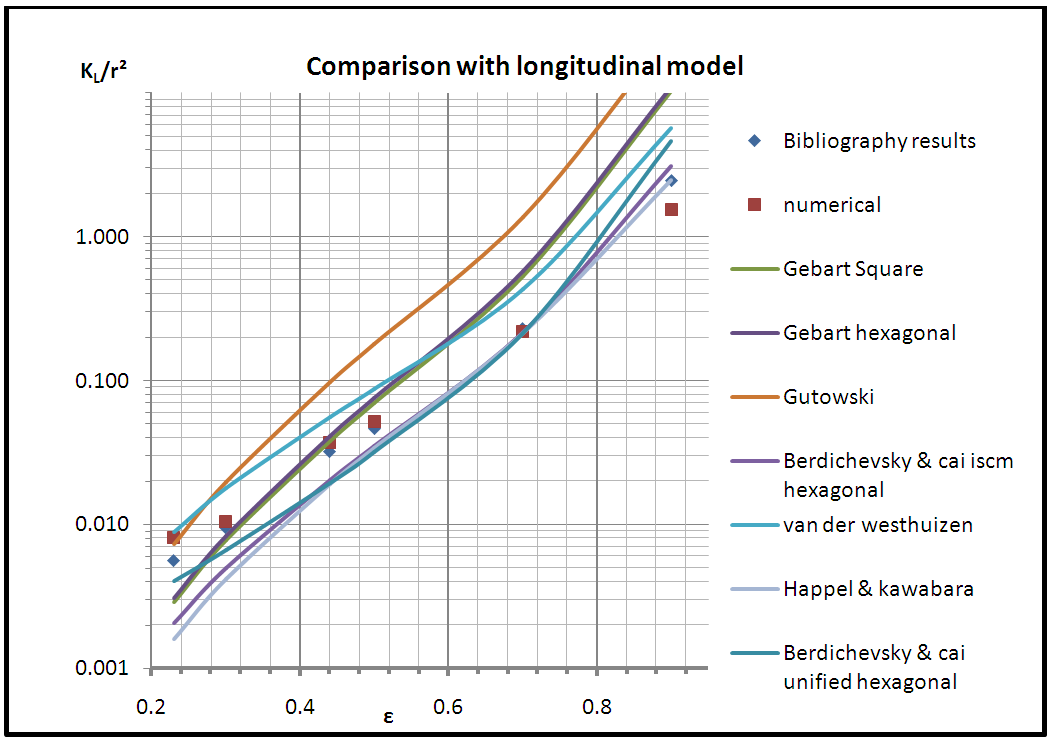 | Chart 1. Comparison between longitudinal models |
|
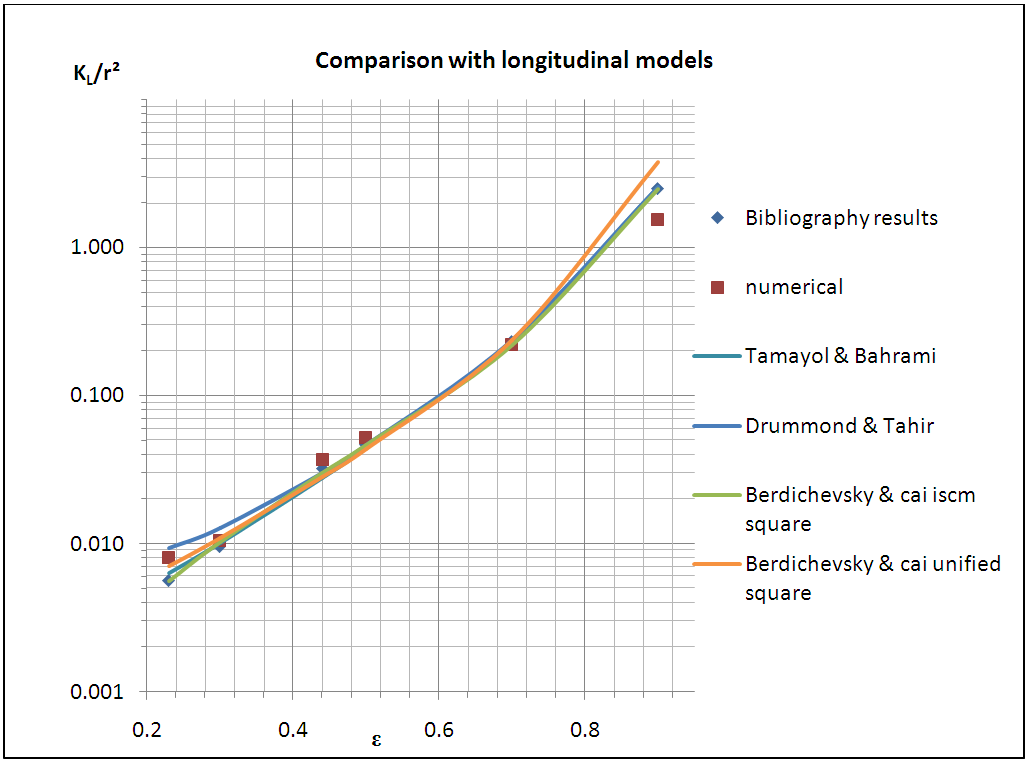 | Chart 2. Comparison between longitudinal models |
3.2.2. Comparison for Transversal Flow (Steady State Mode)
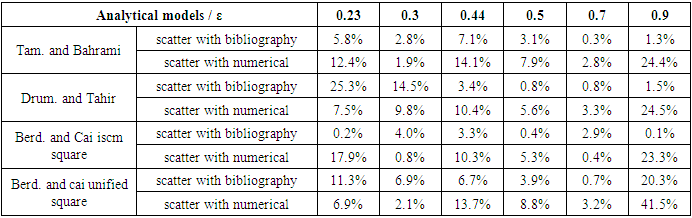
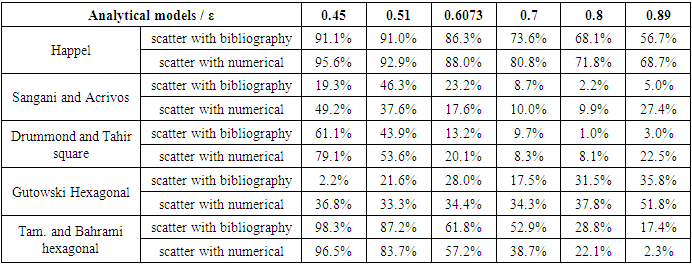
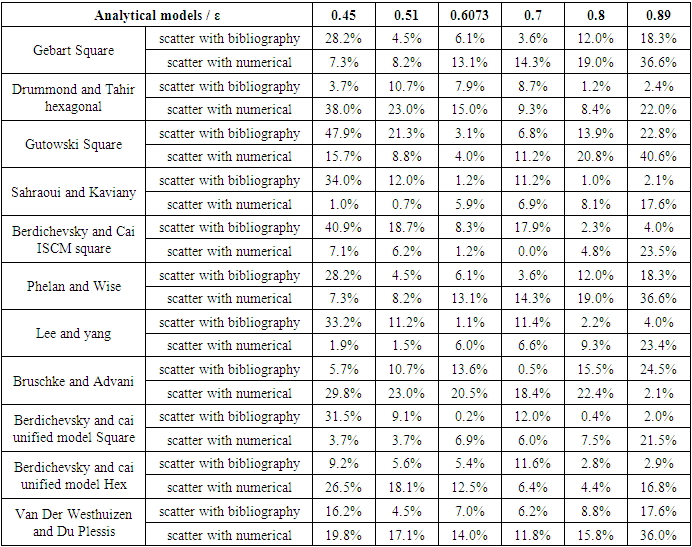
- By referring to Table 14 and Chart 3, Happel shows very high scattering with bibliography results on all selected porosities, with the least scattering equal to 56.7% at porosity 0.89 and greatest one equal to 91.1% at porosity 0.45. The scattering is similarly high with numerical results ranging between 68.7% and 95.6%.Gutowski (hexagonal) reveals distinct scattering values but the overwhelming majority lies between 21.6% and 51.8%.Tamayol and Bahrami (hexagonal) displays great scattering values with the bibliography results on one hand and with the numerical results on the other hand, which range between 17.4% and 98.3%. The models having great scatter with the bibliography and numerical results are excluded from the study. Those are Happel, Gutowski (hexagonal), and Tamayol and Bahrami (hexagonal) models. Both models Sangani and Acrivos and Drummond and Tahir (square) when compared with both bibliography and numerical results show big scattering at lower porosities and smaller scattering values at higher porosities, which reveals the ineffectiveness of these models in our study. The comparison of Sangani and Acrivos results with the bibliography results show scattering values 8.7%, 2.2% and 5.0% at porosities 0.7, 0.8, and 0.89 respectively; while the scattering is high at lower porosities (19.3%, 46.3%, 23.2%). Similarly, when compared to the numerical results, the scattering values are divided into two halves, some are high and the others are relatively low. Drummond and Tahir scattering values with numerical and bibliography values are mostly greater than 20% at the first three porosities, and lower than 20% at the next three ones.
|
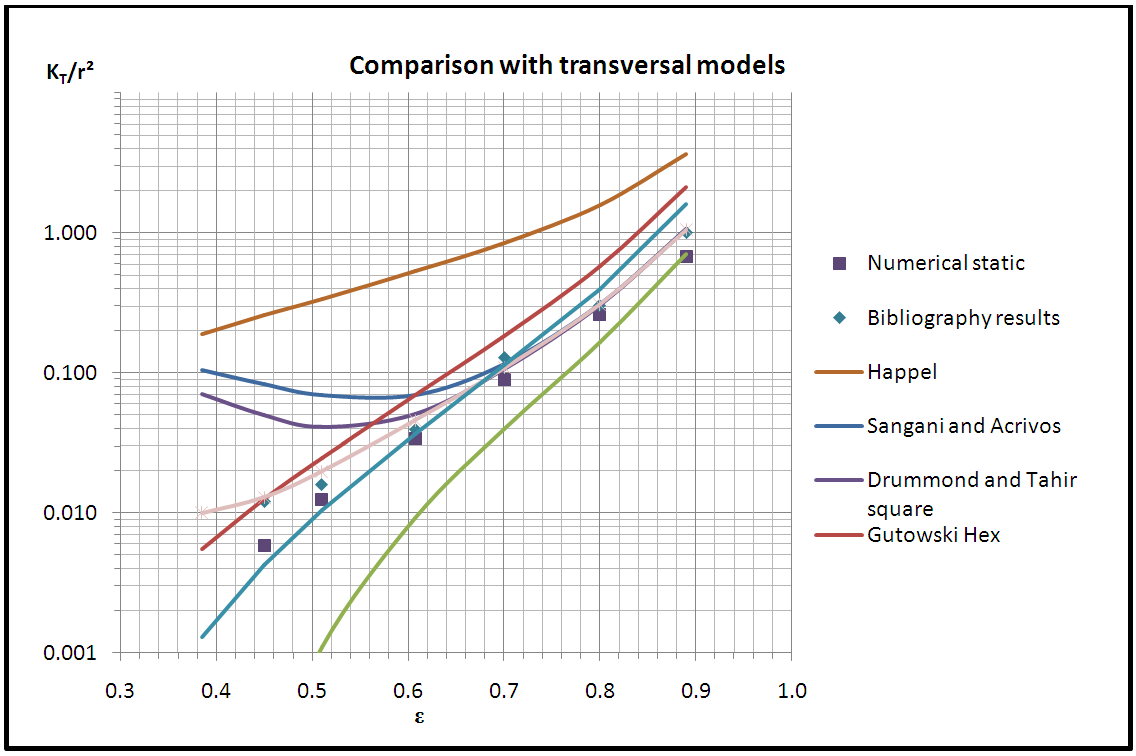 | Chart 3. Comparison between transversal models |
|
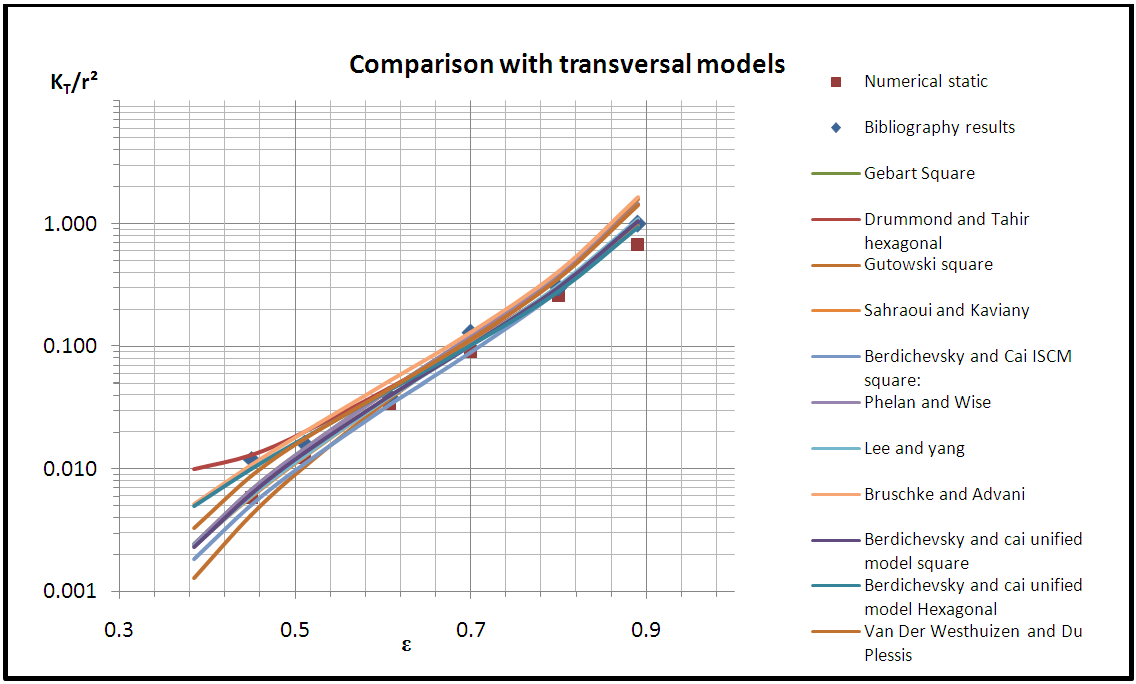 | Chart 4. Comparison between transversal models |
|
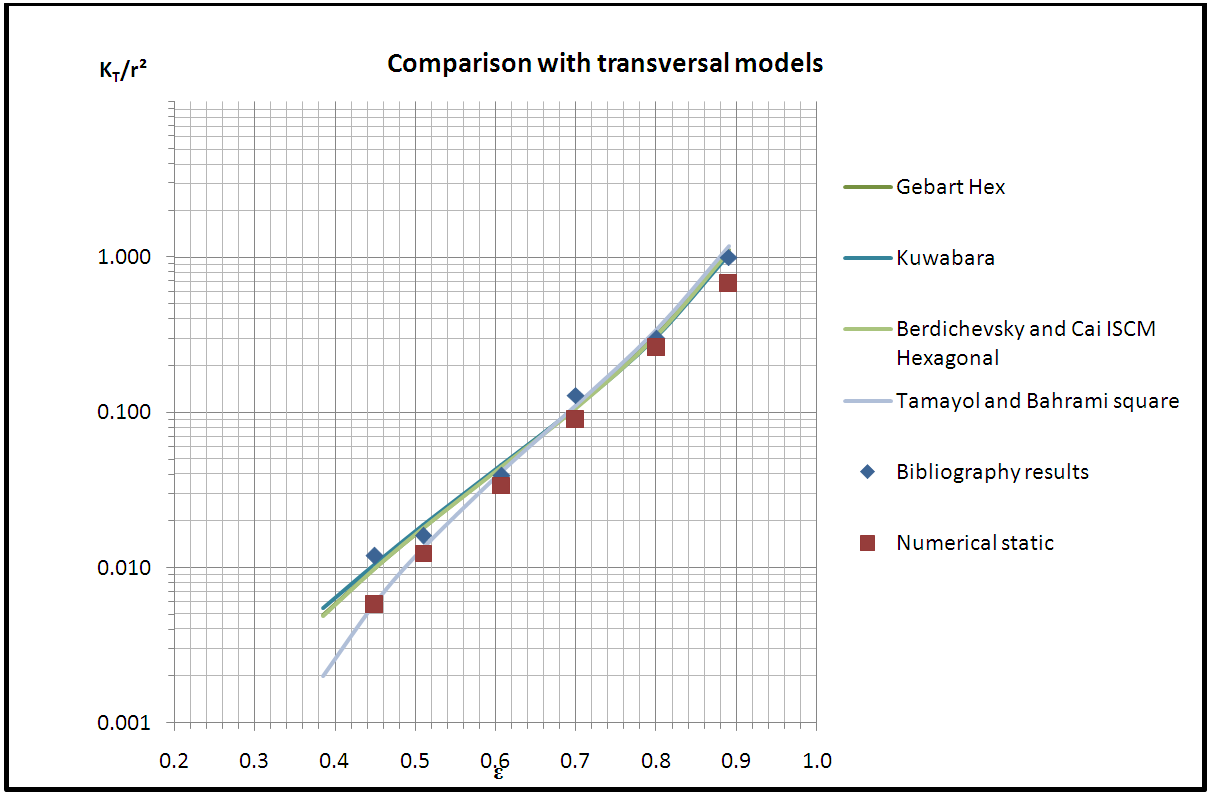 | Chart 5. Comparison with transversal models |
4. Numerical Simulation in a Transient Free Boundary Problem Mode
- In the previous section the transversal numerical simulation was performed in a steady state mode in which a single phase problem was solved, where the studied fluid is located in the saturated region Figure 7. The capillary pressure and surface tension were neglected; thus the measured microscopic permeability value was the transversal saturated microscopic permeability.
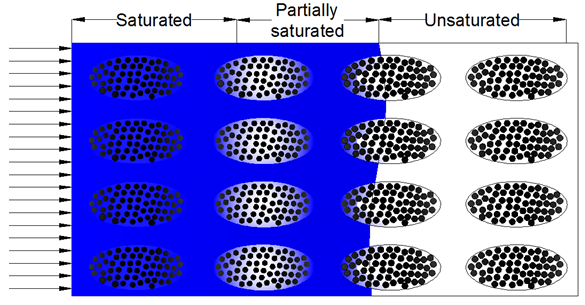 | Figure 7. Flow front progression |
4.1. Simulation Parameters in Transient Mode
- The two fluids selected in this simulation are: Air and Epoxy Resin. Same meshing technique and boundary conditions are used when simulating in a transient mode, whereas, different parameters are took into consideration when the transient simulation is performed, which are the surface tension, mobility, and relative tolerance.
4.1.1. Surface Tension
- The COMSOL MULTIPHYSICS allows the calculation of capillary pressure between each two fibers. Capillary pressure is the necessary pressure to force “non-wetting fluid” to displace the “wetting fluid” in a capillary. Capillary pressure [32] can be mathematically expressed as Pc, equation (6); where Pnw and Pw are the pressures of the non-wetting phase and wetting phase across the interface
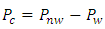 | (6) |
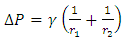 | (7) |
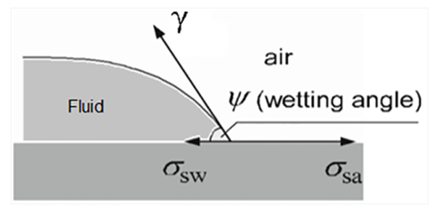 | Figure 8. Wetting angle between fluid and surface |
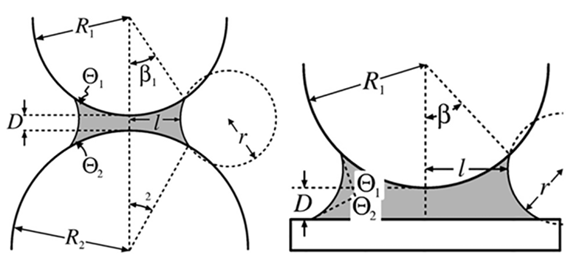 | Figure 9. Fluid subjected to capillary forces in sphere-sphere or sphere-plane geometries [33] |
|
4.1.2. Mobility and Relative Tolerance
- The mobility is related to the time-scale of the Cahn-Hiliard diffusion and therefore governs the diffusion-related time scale of the interface. The χ parameter should be optimized to maintain a constant interface thickness and avoid damping the convective motion. A very high mobility can also lead to excessive diffusion of droplets [34]. Relative tolerance is the permitted variation in some measures and characteristics of an object or work piece. It indicates the precision of reading flow time results.
4.2. Results for Transient Simulation
- The flow front position is recorded at different selected filling time intervals, after extracting the set of results of filling time and correspondent flow front position. The elementary permeability is calculated using Darcy’s law. Then the total permeability is calculated by interpolating these results. Figure 10 shows the flow front observed at two different positions. The local permeability values at successive positions are calculated based on equation (3); then an average permeability value is calculated using equation (8).
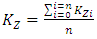 | (8) |
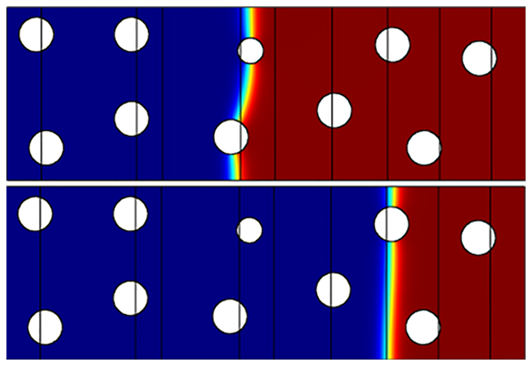 | Figure 10. Flow front observed at two different positions for 0.89 porosity unit cell |
|
4.3. Comparative Study (Transient Mode)
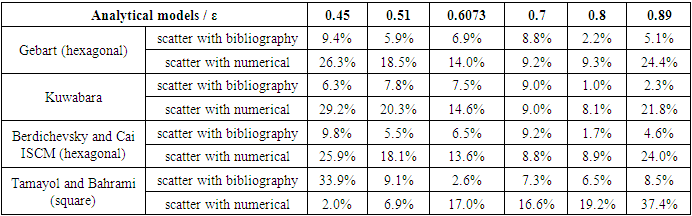
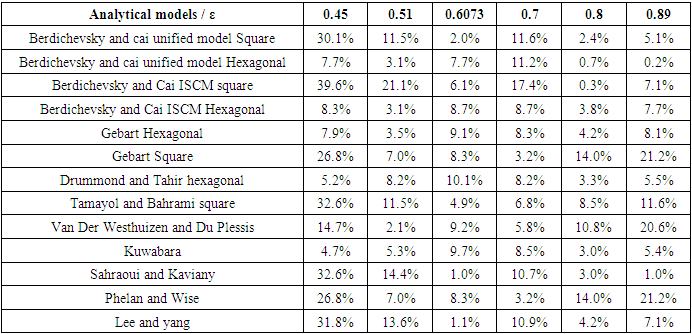
- The models previously selected from the comparative study with steady state mode numerical simulation are subjected to sorting, in which the models with relatively lowest scattering in comparison with numerical simulation in transient mode are considered to be the most suitable for obtaining the transversal microscopic permeability. In this comparative study the chosen models are those having a scattering less than 10%.Table 19 indicates that Berdichevsky and Cai unified model (square) shows three scattering values 2%, 2.4%, and 5.1% which are less than 10%, at porosities 0.6073, 0.8, and 0.89 respectively. On the other hand, the other three values are greater than 10% (30.10% at porosity 0.45, 11.20% at porosity 0.51, and 11.60% at porosity 0.7).Similarly, Berdichevsky and Cai ISCM square, Gebart Square, Tamayol and Bahrami square, Van Der Westhuizen and Du Plessis, Sahraoui and Kaviany, Phelan and Wise, and Lee and yang exhibit in each one of them three values of scattering less than 10% and other three values greater than 10%.Whereas, Berdichevsky and Cai ISCM hexagonal, Gebart hexagonal, Drummond and Tahir hexagonal, and Kuwabara are better relatively, due to the scattering values that are less than 10% at all selected porosities as shown in Table 19.
|
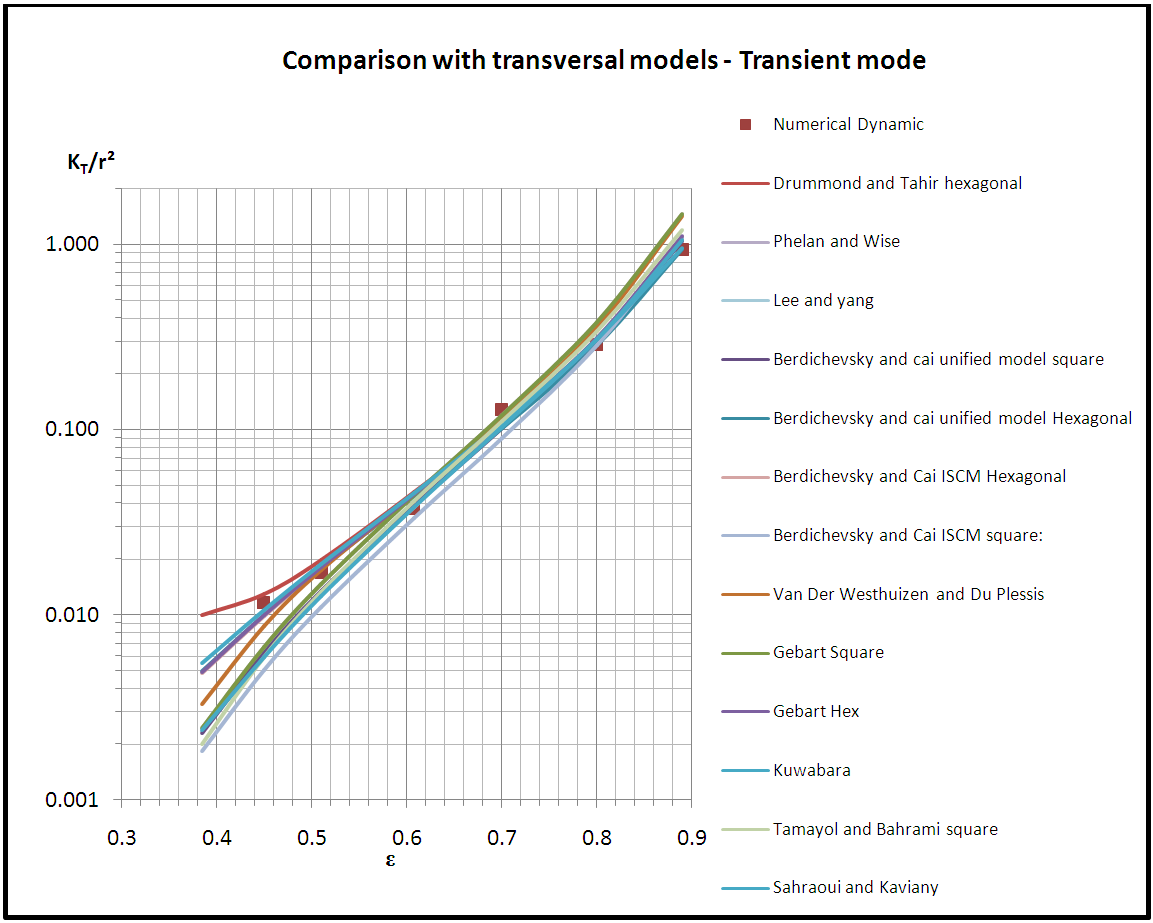 | Chart 6. Comparison with transversal results |
5. Discussion and Analysis
- The comparative studies listed in the previous part of the article are done in order to choose the best models which serve in predicting the microscopic permeability.After performing the comparison between the longitudinal models and the results of the bibliography and numerical simulations in steady state mode, the models Bahrami and Tamayol, Drummond and Tahir, Berdichevsky and Cai ISCM square, and Berdichevsky and Cai unified square are elected to be the most accurate in predicting longitudinal microscopic permeability. This selection was done based on the low scattering values in these comparisons.Regarding the comparative study between the transversal models and the results of the bibliography and numerical simulations in steady state mode, a primary selection was done which highlighted the models that show lower scattering values in comparison with the other models. The selected models are Berdichevsky and Cai unified model Square, Berdichevsky and Cai unified model Hexagonal, Berdichevsky and Cai ISCM Square, Berdichevsky and Cai ISCM Hexagonal, Gebart Hexagonal, Gebart Square, Drummond and Tahir Hexagonal, Tamayol and Bahrami Square, Van Der Westhuizen and Du Plessis, Kuwabara, Sahraoui and Kaviany, Phelan and Wise, and Lee and Yang.Those models are subjected to a secondary selection process which aims to ensure choosing the most convenient models able to fulfill the prediction of transversal microscopic permeability when recommended in any study. This selection process is spread on two steps. First, a numerical simulation in transient mode is done at the same given unit cells previously. This simulation solves a dual phase problem and thus gives permeability value which is more realistic and resembling a real experiment. Second, a comparative study is done between the analytical results of the models and the obtained results from the numerical simulation in transient mode. The models which show the least scattering in this comparison are Berdichevsky and Cai ISCM (hexagonal), Gebart (hexagonal), Drummond and Tahir (hexagonal), and Kuwabara. These selections are the most convenient models for predicting transversal microscopic permeability which is involved in obtaining the permeability tensor value.
6. Conclusions
- The microscopic permeability analytical models were subjected to sorting by comparing their permeability outputs to results derived from other prediction methods. A numerical study was performed, distinguished by utilizing a unit cell with random fiber arrangement which was most representative for real experiment. A comparative study was done between analytical modeling, bibliography, and numerical results. Its analysis presents that Bahrami and Tamayol, Drummond and Tahir, Berdichevsky and Cai ISCM and unified (square) models have good agreement with this data for longitudinal microscopic permeability components. Concerning transverse microscopic permeability, Berdichevsky and Cai ISCM (hexagonal), Gebart (hexagonal), Drummond and Tahir (hexagonal), and Kuwabara models were elected to be the most accurate models. On the other hand, transient mode simulations gave rise to results synchronized with the static mode simulations, which revealed the consistency of the study.The profit of this study is to know the most convenient analytical models to predict the microscopic permeability in unidirectional fiber bundles. Furthermore, in order to calculate an accurate permeability tensor, the value of the microscopic permeability should be obtained precisely. Moreover, the microscopic permeability could be employed in some other studies such as capillary pressure or permeability modeling studies.
Nomenclature
- KL: Longitudinal microscopic permeabilityKT: Transversal microscopic permeabilityε: Resin volume fractionVf: Fiber volume fractionVa: Maximum fiber volume packing factor
Appendix
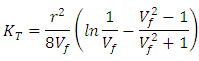 | (Eq.1) |
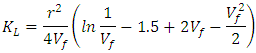 | (Eq.2) |
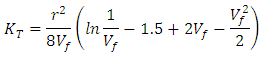 | (Eq.3) |
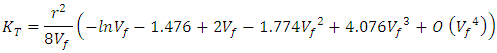 | (Eq.4) |
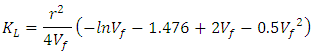 | (Eq.5) |
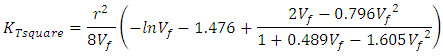 | (Eq.6) |
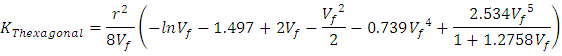 | (Eq.7) |
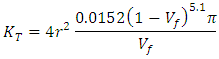 | (Eq.8) |
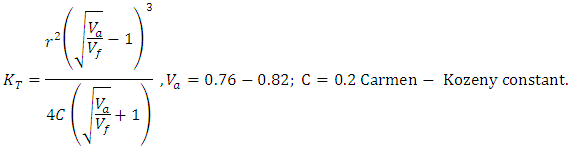 | (Eq.9) |
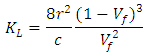 | (Eq.10) |
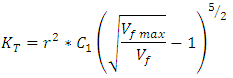 | (Eq.11) |

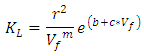 | (Eq.12) |
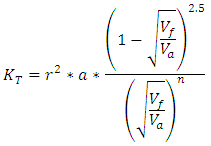 | (Eq.13) |
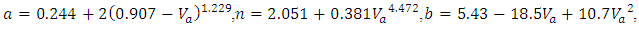
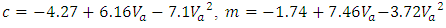
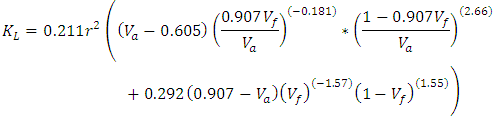 | (Eq.14) |
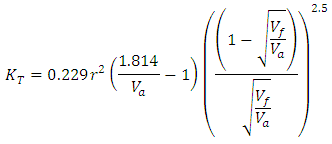 | (Eq.15) |
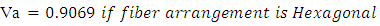
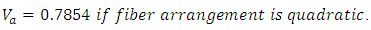
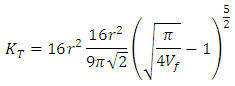 | (Eq.16) |
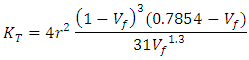 | (Eq.17) |
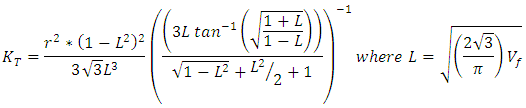 | (Eq.18) |
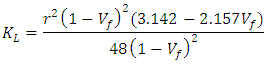 | (Eq.19) |
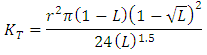 | (Eq.20) |
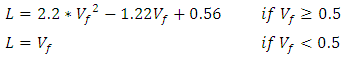
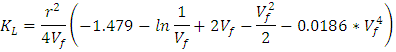 | (Eq.21) |
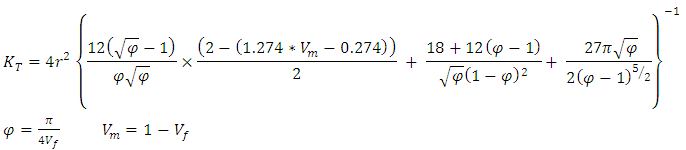 | (Eq.22) |
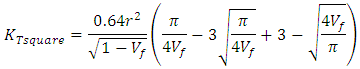 | (Eq.23) |
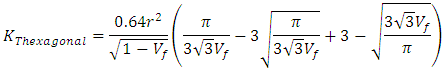 | (Eq.24) |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML