Widayani, Sparisoma Viridi, Siti Nurul Khotimah
Nuclear Physics and Biophysics Research Group, Faculty of Mathematics and Natural Sciences, Institut Teknologi Bandung, Bandung, Indonesia
Correspondence to: Widayani, Nuclear Physics and Biophysics Research Group, Faculty of Mathematics and Natural Sciences, Institut Teknologi Bandung, Bandung, Indonesia.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper reports a theoretical study of stress distribution and factors that affect Young’s modulus of 2D composite model containing circular fillers under compression loads. The dimension used for the composite model containing 1 filler is (4x4) cm with filler radius of 1 cm. In the case of filler more rigid than matrix, the Young’s modulus values used for matrix, filler 1 and filler 2 are close to that of epoxy, Hemp fiber and glass, respectively. In the case of matrix more rigid than filler, we use the same Young’s modulus value of the matrix, and the Young’s modulus of filler 1 and filler 2 are close to LDPE and HDPE, respectively. The stress distribution for 2D composite model containing 2 circular fillers arranged in series and parallel has been carried out for the case filler more rigid than matrix. The dimension used for the composite model containing 2 fillers is (4x7) cm with filler radius of 1 cm. The stress is calculated using Excel and the data are taken for every increment X of 0.1 cm. The results are successfully showing the qualitative picture on stress distribution. The results show that stress is not uniform along X axis, but higher in the area containing the longer more rigid component. Young’s modulus of a specific total filler fraction has been calculated using the method used and compared with Voight and Reuss formulas.
Keywords:
Composite model, Circular filler, Compression load, Stress distribution, Young’s modulus
Cite this paper: Widayani, Sparisoma Viridi, Siti Nurul Khotimah, Theoretical Study on Mechanical Properties of 2-D Composite Models Containing Circular Fillers under Compression Load, International Journal of Composite Materials, Vol. 5 No. 3, 2015, pp. 47-51. doi: 10.5923/j.cmaterials.20150503.01.
1. Introduction
Mostly, the studies on composites focus on the correlation of mechanical properties of the composites with that of its components. The studies are very important since generally researchers concern with new composite materials with specific properties which are actually formed as a combination of its component properties. Proper composition and technique in composites synthesis may result in a new composite with expected mechanical properties.Studies on mechanical properties of composites have been carried out via experiments, modeling and simulation [1-3]. Computational study on mechanical properties of composite containing uniform distribution of hard and soft components has been carried out [4]. The computational results were then compared to calculations based on Voight and Reuss formulas, and the study shows that the Voight formula suits the composite with high fraction of particle. The Voight formula uses isostrain condition where the modulus Young of composites is formulated as follow: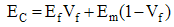 | (1) |
Where EC, Ef, Vf and Em are Young’s modulus of composite, Young’s modulus of fiber, volume fraction of fiber, Young’s modulus of matrix, respectively. Reuss formula, based on isostress condition, is as follow: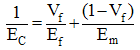 | (2) |
Where EC, Ef, Em, Vf, and Vm are Young’s modulus of composite, Young’s modulus of filler, Young’s modulus of matrix, volume fraction filler and volume fraction of matrix, respectively. There are some other formulations to predict the Young’s modulus of composite based on Young’s modulus of its components such as Einstein formula which is then modified by Guth and Money, Hapin and Tsai formula, etc [5].Fillers can have form typically of spherical [6, 7], ellipsoidal [8], and arbitrary [9], where they can also be non-metallic [3], inorganic [6], or metallic [10].This paper presents a simple view on mechanical property of composite model 2-D containing circular fillers under external compression loads. This model can be considered as simplification of 3D composite model containing spherical fillers, where spherical filler can be approximated by series of cylinder in order to apply fiber refinforcement theory [11]. It has been shown that residual stress in polymeric composites depends on filler shape [12]. In this study, the stress distribution is calculated along X- axis (in horizontal direction) on 2D composite model with one and two fillers. There are two arrangements of filler for the model with two fillers: series and parallel. The basic concept used in this study is that the composites experience contraction under external compression load.
2. Theory
According to elasticity theory, the rigidity of materials is represented by its modulus of elasticity. For normal loads, modulus elasticity is named as Young’s modulus. There are two types of normal load: tensile and compression. In general, response of materials to external tensile load is different with that of compression load. Therefore, Young’s modulus of a material under tensile load may different with that of under compression load. Young’s modulus (E) is a ratio of stress 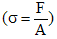 to strain
to strain 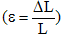 of a material under an external normal load.For a material containing two components connected in series, the external force will be equally transmitted for the two components, thus if there is no difference in area, the two components will experience same stress.
of a material under an external normal load.For a material containing two components connected in series, the external force will be equally transmitted for the two components, thus if there is no difference in area, the two components will experience same stress. 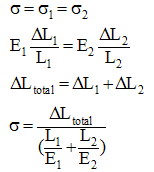 | (3) |
A composite material consists of two components: matrix and filler. This study concerns with 2D composite models with one and two circular fillers. Schematic figure of the composite models are shown in Figure 1. 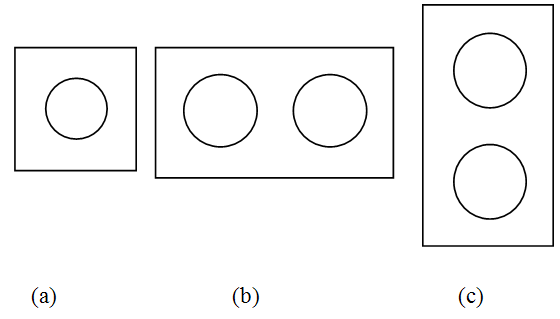 | Figure 1. Schematic of 2D composite models containing circular fillers: (a) one filler; (b) two fillers in series; (c) two fillers in parallel |
3. Method
The dimension used for 2D Composite Model containing 1 filler is (4x4) cm and the filler radius is 1 cm. We use X and Y axis as in the Figure 2 which shows the how the length of filler and matrix is calculated at a specific X. The filler is located in the middle of the composite, the centre of the filler is at position (2,2) cm. The compression load is along Y axis. The length of both matrix and filler components are varied along X axis.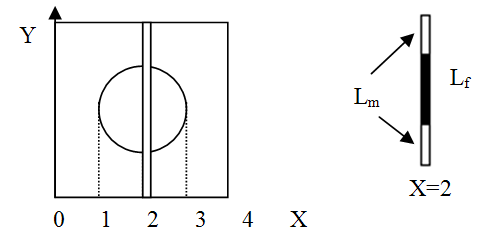 | Figure 2. Illustration of X-axis used for 2D composite model containing 1 filler. At X=2, there are two parts of matrix and one part of filler arranged in series |
Similar approach is used for the two other models: 2D composite models containing 2 circular fillers arranged in series with the dimension of (7x4) cm and parallel with the dimension of (4x7) cm. The radius of every filler is 1 cm. Position of the centre of the fillers for composite containing series and parallel fillers are at (2,2) cm and (5,2) cm; and (2,2) cm and (2,5) cm, respectively. Using this approach, the length of matrix and filler at specific X ranges can be calculated and they are shown in Table 1.Table 1. The length of matrix (LM) and filler (LF)
 |
| |
|
All the calculations are conducted using excel program.
4. Results and Analysis
The total extension is the same for every X position, which is the sum of extension of matrix and filler. The value of stress at area that containing only matrix is 1000 Pa. Using equation (3) and the data in Table 1, the value of stress at other area can be calculated. The stress is calculated for every increment X of 0.01 m. The Young’s modulus data of the components used in the calculation are based on online data [13].
4.1. Stress Distribution for 2D Composite Model Containing 1 Circular Filler
There are two cases for 2D Composite Model containing 1 circular filler: (1) filler stiffer than matrix, and (2) matrix stiffer than filler. The Young’s modulus for case (1) are E matriks = 2 GPa (close to epoxy), E filler 1 = 35 GPa (close to Hemp fiber), E filler 2 = 50 GPa (close to glass). The results are shown in Figure 3 (a) as stress 1 and stress 2 for filler 1 and filler 2, respectively. The Young’s modulus for case (2) are E matriks = 2 GPa (close to epoxy), E filler 1 = 0.11 GPa (close to LDPE), E filler 2 = 0.8 GPa (close to HDPE). The results are shown in Figure 3 (b) as stress 1 and stress 2 for filler 1 and filler 2, respectively. Figure 3 shows that the stress is not homogeneously distributed. This is because of the presence of filler. As expected, higher stress occurs at the area containing stiffer components.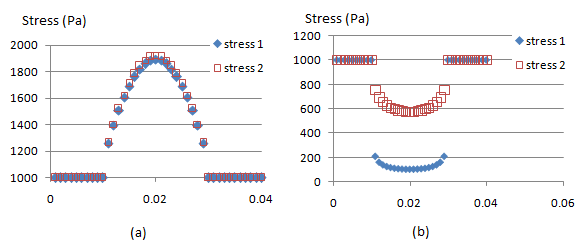 | Figure 3. Stress Distribution for 2D Composite Model containing 1 circular filler: (a) case 1 the filler is stiffer than matrix, and (b) case 2 the matrix is stiffer than filler |
4.2. Stress Distribution for 2D Composite Model Containing 2 Circular Fillers
For 2D composite model containing 2 circular fillers, we use filler that is stiffer than the matrix. There are two cases: (1) the two fillers are arranged in series, and (2) the two fillers are arranged in parallel. The Young’s modulus of the components are E matriks = 2 GPa (close to epoxy), E filler 1 = 35 GPa (close to Hemp fiber), E filler 2 = 50 GPa (close to glass). The results are shown in Figure 4 as stress 1 and stress 2, for filler 1 and filler 2, respectively. Similar with composite containing 1 filler, higher stress occurs at the area containing longer stiffer components. Figure 4 also shows that composite containing parallel filler shows higher maximum stress compared to that of series filler. The result indicates that the stress distribution is influenced by filler arrangement. 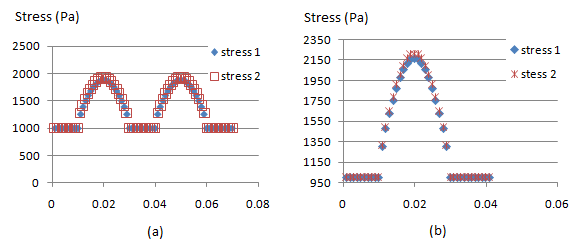 | Figure 4. Stress distribution for 2D Composite Model containing 2 circular fillers for the two types of filler arrangement: (a) series, and (b) parallel |
4.3. The Influence of Filler Arrangement and Filler Fraction on Young’s Modulus of 2D Composite Model Containing Circular Fillers
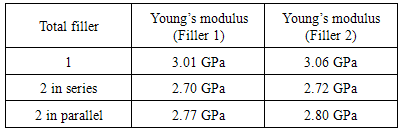
Young’s modulus of a composite is ratio of stress to strain experienced by the composite. In this study, the stress of a composite model is average of the stress values along the X axis and the strain is equal to the total strain. The filler fraction for 2D composite model containing 2 fillers must be similar for both series and parallel arrangement. Using the composite dimension of (4x7) cm and the radius of every filler is 1 cm, it can be calculated that the filler fraction is 22%. In order to study the influence of number of filler, the Young’s modulus of 2D composite model containing 1 filler that has same filler fraction, 22%, has been calculated. This composite model has a dimension of (7x4) cm and the filler with radius 1.41 cm is centred at (3.5,2) cm. All the Young’s modulus obtained from the calculation is shown in Table 2. The Young’s moduli of matrix, filler 1 and filler 2 are 2 GPa, 35 GPa, and 50 GPa, respectively. Table 2. Young’s modulus of 2D composite model with total filler fraction of 22%
 |
| |
|
Table 2 shows that for the same filler fraction, higher number of filler gives lower value of Young’s modulus. The Young’s modulus of 2D composite containing 1 filler is higher than that of containing 2 fillers both in series and parallel. It may relate to contact area between components in the composite, where higher contact area results in lower stiffness. This may relate to bonding between matrix and filler, as the contact area is the location of bonding between them. Concerning 2D composite model containing 2 circular fillers, it can be seen that Young’s modulus of the composite also depends on how the fillers are arranged. Parallel arrangement results in higher value than that of series arrangement.To compare with the Voight and Reuss formulas, the Young’s modulus of composite with the same condition (equal Young’s modulus for every component and filler fraction) has been calculated using equation (1) and (2). The Young’s modulus of composite calculated using Voight formula using filler 1 and 2 is 9.25 GPa and 12.55 GPa, respectively. The Young’s modulus of composite calculated using Reuss formula using filler 1 and 2 is 2.52 GPa and 2.53 GPa, respectively. It is known that Voight and Reuss formulas give the upper and lower limit of Young’s modulus of composites, respectively. As can be seen in Table 2, the calculated Young’s moduli are lower than Young’s modulus calculated by Voight formula but upper than that of Reuss formula.
5. Conclusions
This theoretical study on mechanical property of 2D composite model containing circular fillers shows the stress distribution on the composites. An area containing longer stiffer component has a higher stress. The stress distribution is influenced by the arrangement of the fillers. From the calculation of Young’s modulus of 2D composite model containing circular fillers, it can be concluded that Young’s modulus is not only affected by filler fraction, but also by the number and arrangement of fillers. For an equal filler fraction, higher number of filler gives lower value of Young’s modulus and parallel filler gives higher Young’s modulus than series filler. All the calculated Young’s modulus is higher than Young’s modulus calculated using Reuss formula but lower than that is calculated using Voight formula.
ACKNOWLEDGEMENTS
The authors express gratitude to Institut Teknologi Bandung, and Ministry of Higher Education and Research, Indonesia for supporting facility during this work through “Penelitian Unggulan Perguruan Tinggi – Riset Desentralisasi Dikti” with contract number 310i/I1.C01/PL/2015.
References
| [1] | Widayani, Yati Susanah, Linda Sekar Utami, Siti Nurul Khotimah, Sparisoma Viridi, "Compressive elastik modulus of natural fiber based binary composites", International Conference on Physics and Its Application (ICPAP-2011), November 10-11, 2011, Bandung, Indonesia; AIP Conf Proc. (2012), pp. 286-289. |
| [2] | Sparisoma Viridi, Widayani, and Siti Nurul Khotimah, "2-D Granular Model of Composite Elastikity using Molecular Dynamics Simulation, International Conference on Physics and Its Application (ICPAP-2011)November 10-11, 2011, Bandung, Indonesia, AIP Conf. Proc. (2012), pp. 219-222. |
| [3] | Irfan Dwi Aditya, Widayani, Sparisoma Viridi, and Siti Nurul Khotimah; "Study Of Internal Response Of Epoxy Due To Compressive Load Via Experiment And Simulation Using Abaqus FEA Sofware, Advanced Materials Research Vol. 896 (2014) pp 549-552 @ (2014) Trans Tech Publications, Switzerland doi:10.4028/www.scientific.net/AMR.896AMR.896.549. |
| [4] | Hyoung Seop Kim, Sun Ig Hong, Sun Jae Kim; On the rule of mixtures for predicting the mechanical properties of composites with homogeneously distributed soft and hard particles; Journal of Materials Processing Technology 112 (2001) 109-113. |
| [5] | Shao-Yun Fu, Xi-Qiao Feng, Bernd Lauke, Yiu-Wing Mai, Effects of particle size, particle/matrix interface adhesion and particle loading on mechanical properties of particulate–polymer composites, Composites: Part B 39 (2008) 933–961, Science Direct, 2008. |
| [6] | H. Lu, Y. K. Lee, M. Oguri, J. M. Powers, Properties of a dental resin composite with a spherical inorganic filler, Operative Densitry 31 (2006), 734-740. |
| [7] | T. Glaskova, M. Zarrelli, A. Borisova, K. Timchenko, A. Aniskevich, M. Giordano, Method of quantitative analysis of filler dispersion in composite systems with spherical inclusions, Composites Science and Technology 71 (2011) 1543-1549. |
| [8] | M. Taya, T. –W. Chou, On two kinds of ellipsoidal inhomogeneities in an infinite elastic body: An application to a hybrid composite, International Journal of Solids and Structures 17 (1981), 553-563. |
| [9] | H. Li, J. Yang, Z. Li, An approximate solution for the plane stress model I crack interacting with an inclusion of arbitrary shape, Engineering Fracture Mechanics 116 (2014) 190-196. |
| [10] | D. M. Bigg, Rheological analysis of highly loaded polymeric composites filled with non-agglomerating spherical filler particles, Polymer Engineering and Science 22 (1982), 512-518. |
| [11] | J. Leidner, R. T Woodhams, The strength of polymeric composites containing spherical fillers, Journal of Applied Polymers Science 18 (1974) 1639-1654. |
| [12] | L. Nicolais, R. A. Mashelkar, The strength of polymeric composites containing spherical fillers, Journal of Applied Polymer Science 20 (1976) 561-563. |
| [13] | www.EngineeringToolbox.com Tensile Modulus – Modulus of Elasticity or Young’s Modulus for some common Materials, Retrieved 23-4-2015. |
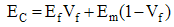
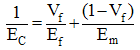
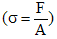 to strain
to strain 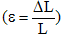 of a material under an external normal load.For a material containing two components connected in series, the external force will be equally transmitted for the two components, thus if there is no difference in area, the two components will experience same stress.
of a material under an external normal load.For a material containing two components connected in series, the external force will be equally transmitted for the two components, thus if there is no difference in area, the two components will experience same stress. 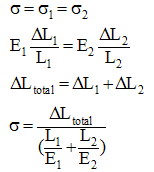




 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
