Amós Magalhães de Souza1, Luciano Donizeti Varanda1, André Luis Christoforo2, Maria Fátima do Nascimento1, Sabrina Fernanda Sartório Poleto1, Tulio Hallak Panzera3, Francisco Antonio Rocco Lahr1
1Department of Materials Science and Engineering, São Carlos Engineering School, São Paulo University - USP, Av. Trabalhador São-carlense, 400, Centro, zip code 13566-590, São Carlos, SP, Brazil
2Department of Civil Engineering, Federal University of São Carlos - UFSCar. Washington Luís highway, km 235 – SP 310, Guanabara garden, zip code 13565-905, São Carlos, SP, Brazil
3Department of Mechanical Engineering, Federal University of São João del-Rei, São João del-Rei, 36307-352, Brazil
Correspondence to: André Luis Christoforo, Department of Civil Engineering, Federal University of São Carlos - UFSCar. Washington Luís highway, km 235 – SP 310, Guanabara garden, zip code 13565-905, São Carlos, SP, Brazil.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
OSB (oriented strand boards) are wood based products that substitute plywood boards, usually used as structural elements, especially with part of formwork for reinforced concrete members as beams, slabs and columns. In this context, the stiffness properties are highly important. This study aimed to evaluate, with the aided of three points static bending test, the modulus of elasticity of OSB using recommendations of the European Standard EN 310:1993, combined with an alternative method of calculation based on the least square method. In this case, three displacement values are taking in account to stiffness determination, improving reliability on it. Results of the ANOVA indicated no statistical equivalence between moduli of elasticity obtained by the two methods of calculation. Modulus of elasticity of this technique proved to be 7% lower than the elastic modulus obtained by standard EN 310:1993, revealing be important the use of suggested approach.
Keywords:
Modulus of elasticity, Bending, Composites, Oriented strand board
Cite this paper: Amós Magalhães de Souza, Luciano Donizeti Varanda, André Luis Christoforo, Maria Fátima do Nascimento, Sabrina Fernanda Sartório Poleto, Tulio Hallak Panzera, Francisco Antonio Rocco Lahr, Modulus of Elasticity in Static Bending for Oriented Strand Board (OSB), International Journal of Composite Materials, Vol. 4 No. 2, 2014, pp. 56-62. doi: 10.5923/j.cmaterials.20140402.03.
1. Introduction
According to European Standard EN 300:2006 [1], OSB (oriented strand boards) are defined as multiple layer panels made from strands (wood strips of a predetermined shape with a length greater than 50mm and a thickness smaller than 2mm), bonded by an adhesive. Strands in outer layers tend to align parallel to the length of the board. In the center layer, strands may be randomly distributed or aligned generally in a perpendicular direction to the outer layers.The Structural Board Association [2] mentions that OSB are generally composed of three to five layers and that the arrangement of longitudinal strands in outer layers increases panel strength and stiffness in the direction of alignment. At the same time, the production process induces a properties reduction in the perpendicular direction to the panel length.Among OSB mechanical properties, it should be noted the modulus of elasticity in static bending (MOE), an essential parameter to performance evaluation in structural designs, since these panels were developed primarily for such applications, as substitute for plywood.MOE values are obtained according to assumptions of static bending behavior, under test conditions contained in regulatory documents. However, these are not methods based on criteria of optimization, since the stiffness is evaluated using the slope of the linear elastic part of the stress × strain diagram, or knowledge of two levels of stress and strain, successively measured in the region of proportionality between stress and strain [3, 4]. With the aid of the three points static bending test, this study evaluated the modulus of elasticity of OSB, using the calculus assumptions recommended by European standard EN 310:1993 [5] and, as alternative, employing an approach to calculation based on the least squares method, taking into account the information of three displacement values in stiffness calculating, as a way to reach the desirable improvement of MOE reliability.Assumptions of standard EN 310:1993 [5] were adopted. In Brazil, a specific code on evaluation OSB performance is not yet available.
2. Material and Methods
For OSB production, in this study, the strands were obtained from refused structural pieces of Pinus sp. According to Bortoletto and Garcia [6], Saldanha [7], Saldanha and Iwakiri [8] and Surdi [9], this specie presents density compatible to OSB manufacture [10].As adhesive, castor oil polyurethane resin was employed. This resin was chosen considering its excellent performance, as related in papers authored by Dias [11], Nascimento et al. [12], Bertoloni [13] and Ferro [14].To OSB production, the following equipments were used: circular saw; knife mill, particles generator; stove; analytical balance; gluing equipment; particle separator; mixer; digital caliper and hydraulic press (80t and 200℃ capacity).OSB panels were produced and tested in Wood and Timber Laboratory, Structural Department, São Carlos Engineering School, São Paulo University.OSB production process followed parameters proposed by Mendes et al. [15]. Initially, joists of Pinus sp (rejected for building purposes), moisture content near 12%, were referred for joinery, where were cut in pieces 90mm wide and 45mm thick (Figure 1). Such dimensions established length and width of the particles, generated on a disc chipper, whose knives were adjusted to furnish thicknesses between 0.40 and 0.90mm. | Figure 1. Strands production |
Strands were weighed and contained in gluing equipment, in which adhesive distribution was carried out by spraying, with the aid of an air compressor and two pistols (Figure 2). Firstly, the polyol was applied and, then, the prepolymer [16, 17]. Based on Bertolini [13], weight ratio of polyol and prepolymer was adopted 1:1. Following studies authored by Dias [11] and Nascimento et al. [12], resin content for all panels was 12%, based on the dry weight of the particles. Strands were glued on the separator set (Figure 3) positioned to perform the guidance and shaping of the mattress. | Figure 2. Resin application (a) and strands getting out gluing equipment (b) |
 | Figure 3. Strands orientation (a), outer layer (b), inner layer (c) and mattress (d) |
A pre-pressing was conducted aiming to improve mattress conformation and to avoid particles loss. Then, the mattress was taken to a hydraulic press and subjected to specific pressure of 4.5MPa, during ten minutes at a temperature of 100℃, as recommended by Mendes et al. [15] and Nascimento et al. [12].After production, OSB panels remained 72 hours in cure process to ensure good performance to adhesive.Three layers were adopted: outer (two) with strands in same direction and inner with randomic distribution. Following Iwakiri et al. [18], a proportion (face, inner, face) 20:60:20 was chosen, based on dry particles weight.Four panels were manufactured, with nominal dimensions 350×350×10mm. Each panel provided six specimens with dimensions 250×50×10mm, as recommended by EN 310:1993 [5]. Thus, 24 samples were tested in static bending.Figures 4a and 4b show structural models test (three points static bending) employed to evaluate modulus of elasticity obeying EN310:1995 [5] recommendations and using alternative approach, respectively.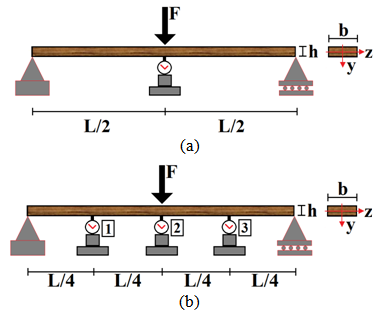 | Figure 4. Structural models test |
The displacement (δ) at the midpoint of the specimen (Figure 4a) is obtained using the Equation 1, coming from the concepts of strength materials. E is the longitudinal modulus of elasticity (or Young's); b and h are cross section width and height, respectively (Figure 4a).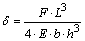 | (1) |
Equation 1, written in function of the elastic modulus, is utilized by EN 310:1993 [5] to determine OSB stiffness. Equation 2 establishes the value of the modulus obtained by European Standard (Est); F10%, F40%, δ10% and δ40% are the values of forces and displacements obtained at about 10 and 40% of the maximum force estimated from the experiment.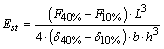 | (2) |
Displacements obtained in deflectometers 1 and 3 (Figure 4b) are expressed by Equation 3, displacement in deflectometer 2 is given by Equation 1, both written in function of E.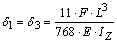 | (3) |
Based on displacements registered by deflectometers 1, 2 and 3 (Figure 4b), and considering Equations 1 and 3, the alternative modulus of elasticity (Eotm) is obtained using the least square method (Equation 4), aiming to determine the value of modulus of elasticity in such way that the generated residue between analytical (δ(E)i) and experimental (δi) displacements come be the smaller possible.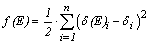 | (4) |
Substituting Equations 1 and 3 into Equation 4, deriving and equating it to zero, the value of the modulus of elasticity to minimize differences between the displacements analytical and experimentally obtained (Equation 5) is then obtained, i.e. the global minimum point, considering the second derivative criterion.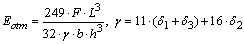 | (5) |
Modulus of elasticity for OSB was calculated using Equations 2 (Est) and 5 (Eotm). Experimental displacements were limited to L/200 [19, 20]. Thus it was possible to consider the tests as “non destructive”, since physical and geometrical linearity were warranted [21]. Equation 5 was employed into displacements between L/300 and L/200, furnishing two values to the so-called "alternative modulus of elasticity" (EL/300, EL/200).Variance analysis was carried out in order to verify equivalence between Est and Eotm from alternative approach (EL/300, EL/200). Tukey test was employed when ANOVA showed statistical significance.Aiming to relate modulus of elasticity obtained following EN 310:1993 [5] requirements with modulus of elasticity calculated by the proposed methodology, the least square method was utilized (Equation 4), adapted to determine coefficient α (Eotm=Est·α).
3. Results and Discussions
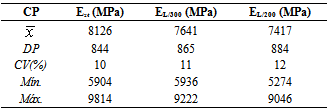
Table 1 shows the modulus of elasticity values (Est; EL/300; EL/200) for OSB, in static bending. In this Table, 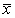 is the sample mean; SD the standard deviation; CV coefficient of variation; Min and Max, the lowest and highest value, respectively.
is the sample mean; SD the standard deviation; CV coefficient of variation; Min and Max, the lowest and highest value, respectively.Table 1. Modulus of elasticity values
 |
| |
|
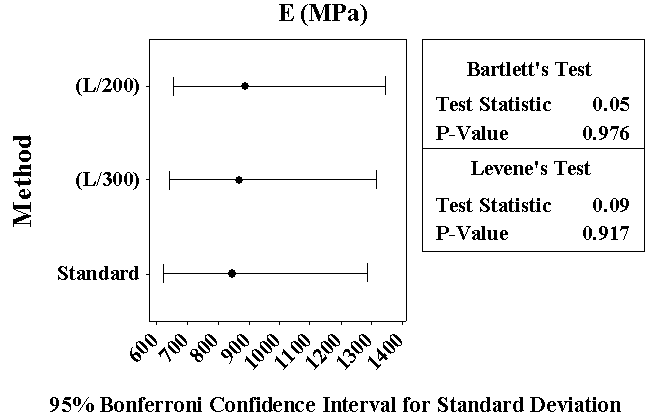
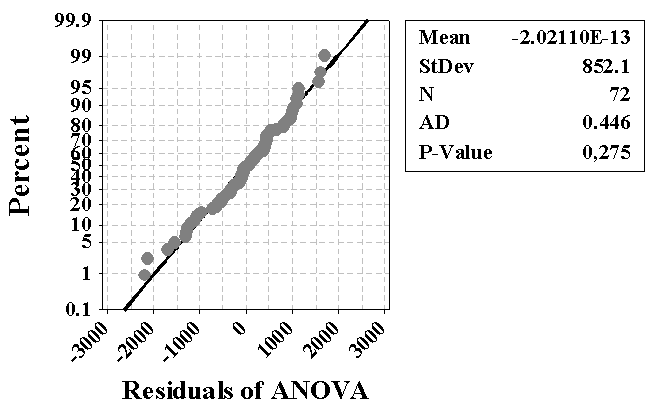
Comparison with normative documents concerning OSB, EN 300:2006 [1], shows that the modulus of elasticity, obtained by European standard and the alternative methodology of calculation, were 69% and 57% higher than the limit value (4800MPa) for the class OSB/4, implying (mechanically) that those panels can be manufactured for use in outdoor and structural applications.Figure 5 illustrates the Anderson-Darling graphic for E values, ensuring that data follow a Gauss distribution, once P-value (0,486) is superior to 5% [22].Figure 6 presents results about the hypothesis test of equivalent variances, reliability level 5%. H0, the null hypothesis, considers equivalent variances. Bartlett and Levine tests furnish P-values superior to 0.05 and, so, H0 is accepted, validating the ANOVA model.Variance analysis of the factor “calculation method” led to a P-value inferior to 5% (0.019), confirming that it's a significant factor to determine OSB modulus of elasticity in static bending.Figures 7, 8 and 9 show the graphics of normality, homogeneity and residues independence related to ANOVA test.Figure 10 present the graphic of main effects related to factor “calculation method” on OSB modulus of elasticity in static bending. Results revealed that, in the displacements interval (L/200; L/300), the proposed method proportioned values inferior of E if compared to those obtained based on EN 310:1993 [5] recommendations.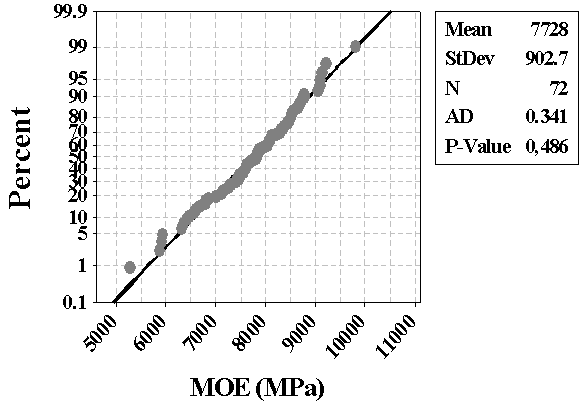 | Figure 5. Normality graphic for E values |
 | Figure 6. Results of hypothesis test for equivalent variances |
 | Figure 7. Graphic of residues normality (ANOVA) |
 | Figure 8. Graphic of residues versus adjusted values |
 | Figure 9. Graphic of residues versus order of observation |
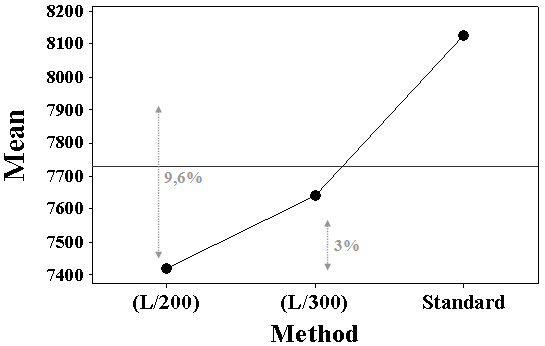 | Figure 10. Graphic of main effects on OSB modulus of elasticity |
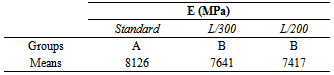
Table 2 presents results of Tukey test for the levels of factor “calculation method”. Moduli of elasticity were equivalent (EL/300, EL/200) but significantly inferior to Est, obtained based on EN 310:1993 [5] recommendations.Table 2. Results of Tukey test to moduli of elasticity
 |
| |
|
Based on the equivalence of moduli of elasticity coming from alternative approach, their mean values were determined and, then, applied the least square method. As the adjusted coefficient (α) reached 0.93, safety conditions suggest that a 7% reduction must be applied on E obtained based on EN 310:1993 [5] recommendations.
4. Conclusions
It was observed that the values of OSB modulus of elasticity, determined by both methods of calculation, were higher than the limit value required by European Standard EN 300:2006 [1], for class OSB/4. So, excellent level of mechanical strength of boards produced in this work got ensured and led to affirm that these panels are suitable for structural and external uses.Results of the statistical analysis indicated non-equivalence between moduli of elasticity, determined by the alternative approach, to those obtained base on European standard requirements. It’s possible to suggest that modulus of elasticity obtained according to EN 310:1993 [5] must be corrected in favor of safety in structural calculations.It is noteworthy that results generalization can be applied after knowing the behavior of OSB into the four classes proposed by European regulatory document.
References
| [1] | European Committee for Standardization - EN 300. Oriented Strand Boards (OSB) - Definitions, classification and specifications, Portugal, 2006. |
| [2] | Structural Board Association. Oriented strand board and waferboard. Technical bulletin. Available from: . Access in: 18 set. 2011. |
| [3] | Silva, A. J. P., Rocco Lahr, F. A., Christoforo, A. L., Panzera, T. H. Properties of sugar cane bagasse to use in OSB. International Journal of Composite Materials, v. 2, p. 50-56, 2012. |
| [4] | Silva, S. A. M., Christoforo, A. L., Ribeiro Filho, S. L. M., Varanda, L. D., Rocco Lahr, F. A. Particleboard manufactured with bicomponent polyurethane resin base on castor oil. International Journal of Composite Material, v. 2, p. 115-118, 2012. |
| [5] | European Committee for Standardization - EN 310, Wood-based panels - Determination of modulus of elasticity in bending and of bending strength, Bruxelas, 1993. |
| [6] | Bortoletto Jr., G; Garcia, J. N. Propriedades de resistência e rigidez à flexão estática de painéis OSB e compensados. Revista Árvore, Viçosa-MG, v.28, n.4, p.563-570, 2004. |
| [7] | Saldanha, L. K. Alternativas tecnológicas para produção de chapas de partículas orientadas “OSB”. 2004, 96 p. Dissertação (Mestrado em Ciências Florestais). Universidade Federal do Paraná, Curitiba, 2004. |
| [8] | Saldanha, L. K.; Iwakiri, S. Influência da densidade e do tipo de resina nas propriedades tecnológicas de painéis OSB de Pinus taeda L. Floresta, Curitiba, v.39, n. 3, p. 571-576, 2009. |
| [9] | Surdi, P. G. Produção de painéis de partículas orientadas (OSB) a partir da madeira de um híbrido de Pinus elliottii var. elliottii e Pinus caribaea var. hondurensis. 2012, 99p. Dissertação (Mestrado Recursos Florestais). Escola Superior de Agricultura Luiz de Queiroz, Piracicaba, 2012. |
| [10] | Souza, A. M. Produção e avaliação do desempenho de painéis de partículas orientadas (OSB) de Pinus sp com inclusão de telas metálicas. 2012. 116 p. Dissertação (Mestrado em Ciência e Engenharia de Materiais). Escola de Engenharia de São Carlos da Universidade de São Paulo, São Carlos, 2012. |
| [11] | Dias, F. M. Aplicação de resina poliuretana à base de mamona na fabricação de painéis de madeira compensada e aglomerada. 2005, 151 p. Tese (Doutorado em Ciência e Engenharia de Materiais). Escola de Engenharia de São Carlos da Universidade de São Paulo, São Carlos, 2005. |
| [12] | Nascimento, M. F.; Rocco Lahr, F. A.; Morales, E. A. M.; Lucato, P. S. L. Aplicação de CPH (Chapas de Partículas Homogêneas) fabricadas com madeiras do nordeste do Brasil e com resíduos de marcenaria. Revista Madeira: Arquitetura e Engenharia. n. 16, 13p., ano 6, Maio.- Agosto. 2005. |
| [13] | Bertolini, M. S. Emprego de resíduos de Pinus sp tratado com preservante CCB na produção de chapas de partículas homogêneas utilizando resina poliuretana à base de mamona. 2011, 126p. Dissertação (Mestrado em Ciência e Engenharia de Materiais). Escola de Engenharia de São Carlos da Universidade de São Paulo, São Carlos, 2011. |
| [14] | Ferro, F. S. Painéis OSB com madeira Schizolobium amazonicum e resina poliuretana à base de óleo de mamona: viabilidade técnica de produção. 2013, 79p. Dissertação (Mestrado em Ciência e Engenharia de Materiais). Escola de Engenharia de São Carlos da Universidade de São Paulo, São Carlos, 2012. |
| [15] | Mendes, L. M.; Iwakiri, S.; Matos, J. L. M.; Keinert Jr., S.; Saldanha, L. K. Pinus spp. na produção de painéis de partículas orientadas (OSB). Ciência Florestal, Santa Maria, v.12, n.2, p. 135-145, 2002. |
| [16] | Silva, S. A. M.; Gonçalves, R.; Campos, C. I.; Rocco Lahr, F. A. Avaliação da resistência à tração perpendicular e da densidade de chapas de fibras de média densidade confeccionadas com resina poliuretana monocomponente e bicomponente derivada de óleo de mamona. Revista Minerva, v. 5, p. 235-240, 2008. |
| [17] | Silva, S. A. M.; Christoforo, A. L.; Gonçalves, R.; Rocco Lahr, F. A. Strength properties of medium density fiberboards (MDF) manufactured with Pinus elliottii wood and polyurethane resin derived from castor oil. International Journal of Composite Materials, v. 3, p. 7-14, 2013. |
| [18] | Iwakiri, S.; Mendes, L. M.; Saldanha, L. K. Produção de chapas de partículas orientadas “OSB” de Eucalyptus grandis com diferentes teores de resina, parafina e composição em camadas. Ciência Florestal, Santa Maria, v. 13, n. 1, p. 89-94, 2002. |
| [19] | Associação Brasileira de Normas Técnicas (ABNT) - NBR 7190. Projeto de Estruturas de Madeira. Rio de Janeiro, 1997. |
| [20] | Rocco Lahr, F. A. Sobre a determinação de propriedades de elasticidade da madeira. 1983, 216p. Tese (Doutorado em Engenharia de Estruturas). Escola de Engenharia de São Carlos da Universidade de São Paulo, São Carlos, 1983. |
| [21] | Montgomery, D. C. Design and analysis of experiments. 6a edition, Arizona, John Wiley & Sons Inc., 2005. |




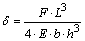
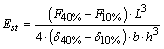
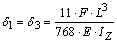
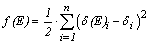
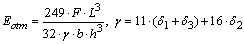
 is the sample mean; SD the standard deviation; CV coefficient of variation; Min and Max, the lowest and highest value, respectively.
is the sample mean; SD the standard deviation; CV coefficient of variation; Min and Max, the lowest and highest value, respectively.





 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
