Miron B. Bekker1, Alexander P. Ugol'nikov2
1Department of Mathematics, University of Pittsburgh at Johnstown, 450 Schoolhouse Rd, Johnstown, USA
2Department of Applied Mathematics, Odessa National Academy of Food Technologies, Ukraine
Correspondence to: Miron B. Bekker, Department of Mathematics, University of Pittsburgh at Johnstown, 450 Schoolhouse Rd, Johnstown, USA.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this article we describe a simple model for thermodynamics of interaction of structure-forming inclusions of a type of a thread (for example, carbon thread) with a matrix compound in composite materials. We provide formulas for free energy, entropy, and heat capacity of such interaction. We assume that a thread is in thermodynamics equilibrium with the compound of the matrix, which we consider as a thermostat. Dynamics of the thread is modeled by the one-dimensional wave equation. On the infinite-dimensional phase space of the thread we consider a Gaussian measure. The partition function of the dynamical system is calculated exactly.
Keywords:
Thread-like inclusion, Gaussian measure, Gibbs distribution, Covariance operator, Vibrating string
Cite this paper: Miron B. Bekker, Alexander P. Ugol'nikov, On Thermodynamics of Interaction of a Thread-Like Inclusion with a Compound of Matrix in Composite Materials, International Journal of Composite Materials, Vol. 4 No. 5A, 2014, pp. 45-48. doi: 10.5923/j.cmaterials.201401.07.
1. Introduction
Composite materials play extremely important role in modern technologies. Composite materials with different types of inclusions as structure-forming elements form a large class of such materials. Studying of properties such materials, processes of their forming is a challenging problem [5-7]. In the present article we introduce a model that describes thermodynamics of interaction of a thread-like inclusion (for example, carbon thread) with a compound of the matrix of a composite material. We assume the thread is in thermodynamics equilibrium with the material of the matrix and describe dynamics of the thread by one-dimensional wave equation with appropriate boundary conditions. Compound of the matrix is considered as a thermostat. On the infinite-dimensional phase space of the thread, we introduce Gibbs measure with the Hamilton function, which describes the oscillation of the thread. Such approach allowed us to evaluate exactly the partition function for our dynamical system. Using the partition function, we calculate free energy, entropy, and heat capacity related to the interaction of the thread and the matrix. To the best of author’s knowledge such approach is new.
2. Gaussian Measure and Partition Function
In this section we provide necessary information about Gaussian measure on infinite-dimensional spaces. Detailed exposition can be found in [1]. We start with some definitions.Definition 1. Let μ be a finite Borel measure on a real separable Hilbert space H with inner product ( , ) and norm  . The measure μ is said to be Gaussian with mean value zero if
. The measure μ is said to be Gaussian with mean value zero if  the function
the function  defined on H has Gaussian distribution with mean zero and variance
defined on H has Gaussian distribution with mean zero and variance 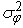 , i.e.
, i.e.
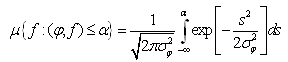 Definition 2. The characteristic functional
Definition 2. The characteristic functional  of a finite Borel measure
of a finite Borel measure  on a Hilbert space H is defined by the formulas
on a Hilbert space H is defined by the formulas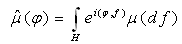 | (1) |
The following theorem is validTheorem 1. A finite Borel measure 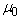 on a Hilbert space H is a Gaussian measure with mean value zero if and only if its characteristic functional is given by
on a Hilbert space H is a Gaussian measure with mean value zero if and only if its characteristic functional is given by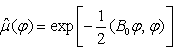 | (2) |
where  is a positive selfadjoint trace class operator on the space H.The operator
is a positive selfadjoint trace class operator on the space H.The operator 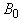 is called the covariance operator and
is called the covariance operator and  .Consider now a dynamical system whose phase space is the space H. We denote the energy of the system in the state
.Consider now a dynamical system whose phase space is the space H. We denote the energy of the system in the state  (Hamiltonian function) by
(Hamiltonian function) by 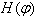 and assume that
and assume that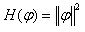 | (3) |
Let 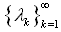 be a sequence of positive numbers (
be a sequence of positive numbers (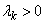 ) such that
) such that  . Without loss of generality we may assume that
. Without loss of generality we may assume that 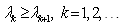 Select and orthonormal basis
Select and orthonormal basis 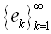 of the space H and define an operator
of the space H and define an operator 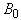 on H as follows:
on H as follows: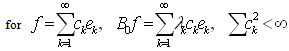 | (4) |
It is clear that B0 is a positive selfadjoint operator of the trace class.Let μ0 be a Gaussian measure μ0 on H with covariance operator B0 and mean value zero.Definition 3. The Gibbs distribution on the phase space H with inverse temperature β (β = 1/T) is a probability Borel measure μ on H which is absolutely continuous with respect to μ0 with the density given by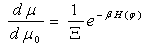 | (5) |
where the partition function Ξ is defined as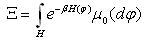 | (6) |
Remark 1. We assume that the temperature T is measured in energy units.Proposition 1. Suppose that condition (3) is fulfilled. Then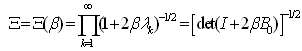 | (7) |
Remark 2. Since the operator B0 belongs to the trace class, the infinite product in (7) converges, and Ξ (β) is an analytic function of β in the half-plane Re β > -1/(2λ1). We will be interested only in values of β > 0.Proof of the proposition is based on straight forward evaluation of the integral (7) as a product of Gaussian integrals.Having the partition function Ξ (β) one easily obtains expression for the thermodynamics Helmholtz free energy of the system (see, for example, [2])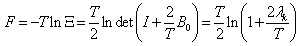 | (8) |
Now using thermodynamics relation one obtains the expression for entropy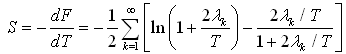 | (9) |
and “heat capacity”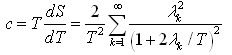 | (10) |
Below we give two examples on applications of formulas above.
3. Vibrating String
In this section we apply previous arguments to the dynamical system described by one-dimensional wave equation. We refer to [3, 4] for necessary information. We consider a vibrating string of the length 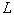 with the linear density
with the linear density  , stretched along the horizontal axis with the force
, stretched along the horizontal axis with the force  . Denote by
. Denote by 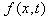 the vertical coordinate of the point of the string with horizontal coordinate
the vertical coordinate of the point of the string with horizontal coordinate  at moment
at moment  . It is well known (see any text book on elementary PDE, for example [3, 4]) that the function
. It is well known (see any text book on elementary PDE, for example [3, 4]) that the function  satisfies the following partial differential equation
satisfies the following partial differential equation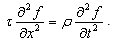 | (11) |
For definiteness we assume that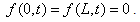 | (12) |
Put , where 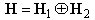

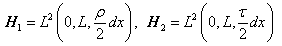 The phase state of the system is completely determined by a vector
The phase state of the system is completely determined by a vector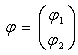 | (13) |
where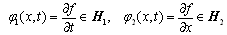 | (14) |
The Hamiltonian of the system is given by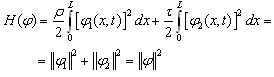 | (15) |
The first term 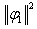 is the kinetic energy of the string, and the second term
is the kinetic energy of the string, and the second term  is its potential energy.A covariance operator
is its potential energy.A covariance operator 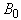 we select in the form
we select in the form 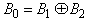 , where
, where 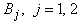 ; are positive trace class operators in the spaces
; are positive trace class operators in the spaces 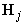 . We select them in the way that reflects boundary conditions (12).Note that the function
. We select them in the way that reflects boundary conditions (12).Note that the function 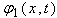 satisfies the same partial differential equation (11) and the same boundary conditions (12) that the function
satisfies the same partial differential equation (11) and the same boundary conditions (12) that the function 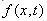
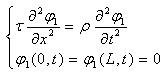 | (16) |
Solving (16) by separation of variables 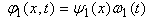 , one obtains for the function
, one obtains for the function 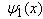 a selfadjoint boundary value problem
a selfadjoint boundary value problem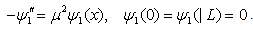 | (17) |
Put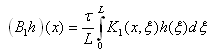 | (18) |
Where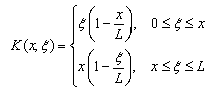 | (19) |
is the Green's function associated with the boundary value problem (17). The coefficient τ ⁄ L has occurred from the requirement that the eigenvalues of the operator B1 have to be in energy units. The operator B1 is selfadjoint and positive, its eigenvalues λ(1)k are up to constant factor reciprocal to the eigenvalues of (17) and they are given by the formula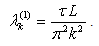 | (20) |
Sinc 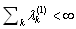 , the operator B1 belongs to the trace class. Normalized eigenvectors e(1)k of the operator B1 are given by
, the operator B1 belongs to the trace class. Normalized eigenvectors e(1)k of the operator B1 are given by
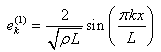 We select B2 in the same form as B1. Thus, the operator
We select B2 in the same form as B1. Thus, the operator  has eigenvalues
has eigenvalues
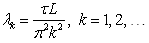 and each
and each  has multiplicity 2.Formula (7) gives
has multiplicity 2.Formula (7) gives
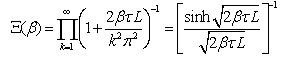 ,where we used the following well-known formula
,where we used the following well-known formula
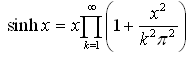 .Formula (8) gives
.Formula (8) gives
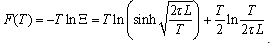 For entropy S one obtains using (9)
For entropy S one obtains using (9)
 and for heat capacity c using (10)
and for heat capacity c using (10)
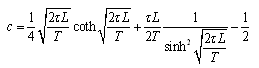 Note that
Note that 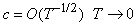 . as
. as
4. Conclusions
We simplified the analytic expressions for thermodynamics of interaction of thread-like inclusions with compound of a matrix in composite materials and our results could be used for modelling of processes of forming structure in such materials. With appropriate modifications, our method can be applied to the cases of two and three dimensional inclusions.
References
| [1] | H. Kuo, “Gaussian Measures in Banach spaces”. Lecture Notes in Math. 463. Springer. Berlin-Heidelberg-New York, 1975. |
| [2] | L.D. Landau, E.M. Lifshitz, “Statistical Physics”, ser. “Theoretical Physics”. Moscow, USSR: Nauka, 1964, vol. 5 (In Russian). |
| [3] | L. Bers, F. John, M. Schchter, “Partial Differential Equations”. New York-London- Sydney, Interscience Publishers, 1964. |
| [4] | M. M. Smirnov, “Partial Differential Equations of Second Order”. Moscow, USSR: Nauka, 1964. (In Russian). |
| [5] | A. N. Herega., 2013, “Physical aspects of self-organization processes in composites. 1. Simulation of percolation clusters of phases and of inner boundaries”. Nanomechanics Science and Technology, 4(2), 119-132. |
| [6] | C. W. Bert., 1977, “Models for Fibrous Composites with Different Properties in Tension and Compression”. J. Eng. Mater. Technol. 99 (4), 344-349. |
| [7] | Decolon Chr. “Analysis of Composite Structures”. Elsevier Science, 2004. |
| [8] | Panin V. E., Likhachev V. A., Grinyaev Y. V. “Structural levels of deformation of solids”. – Novosibirsk, USSR: Nauka, 1985. (In Russian). |
 . The measure μ is said to be Gaussian with mean value zero if
. The measure μ is said to be Gaussian with mean value zero if  the function
the function  defined on H has Gaussian distribution with mean zero and variance
defined on H has Gaussian distribution with mean zero and variance  , i.e.
, i.e.
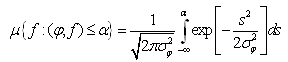 Definition 2. The characteristic functional
Definition 2. The characteristic functional  of a finite Borel measure
of a finite Borel measure 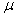 on a Hilbert space H is defined by the formulas
on a Hilbert space H is defined by the formulas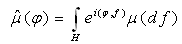
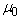 on a Hilbert space H is a Gaussian measure with mean value zero if and only if its characteristic functional is given by
on a Hilbert space H is a Gaussian measure with mean value zero if and only if its characteristic functional is given by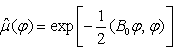
 is a positive selfadjoint trace class operator on the space H.The operator
is a positive selfadjoint trace class operator on the space H.The operator 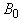 is called the covariance operator and
is called the covariance operator and  .Consider now a dynamical system whose phase space is the space H. We denote the energy of the system in the state
.Consider now a dynamical system whose phase space is the space H. We denote the energy of the system in the state  (Hamiltonian function) by
(Hamiltonian function) by 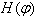 and assume that
and assume that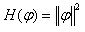
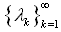 be a sequence of positive numbers (
be a sequence of positive numbers (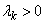 ) such that
) such that  . Without loss of generality we may assume that
. Without loss of generality we may assume that 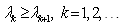 Select and orthonormal basis
Select and orthonormal basis 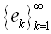 of the space H and define an operator
of the space H and define an operator 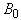 on H as follows:
on H as follows: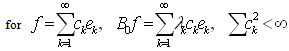
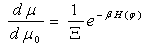
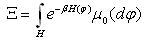
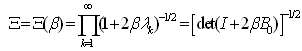
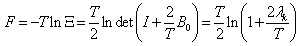
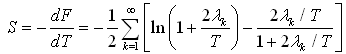
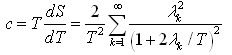
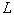 with the linear density
with the linear density  , stretched along the horizontal axis with the force
, stretched along the horizontal axis with the force 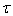 . Denote by
. Denote by 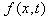 the vertical coordinate of the point of the string with horizontal coordinate
the vertical coordinate of the point of the string with horizontal coordinate  at moment
at moment  . It is well known (see any text book on elementary PDE, for example [3, 4]) that the function
. It is well known (see any text book on elementary PDE, for example [3, 4]) that the function  satisfies the following partial differential equation
satisfies the following partial differential equation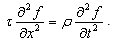
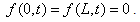
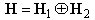

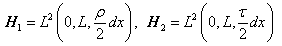 The phase state of the system is completely determined by a vector
The phase state of the system is completely determined by a vector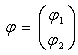
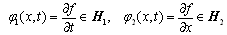
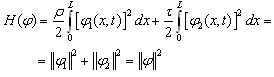
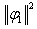 is the kinetic energy of the string, and the second term
is the kinetic energy of the string, and the second term  is its potential energy.A covariance operator
is its potential energy.A covariance operator 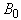 we select in the form
we select in the form 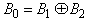 , where
, where 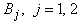 ; are positive trace class operators in the spaces
; are positive trace class operators in the spaces 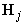 . We select them in the way that reflects boundary conditions (12).Note that the function
. We select them in the way that reflects boundary conditions (12).Note that the function 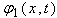 satisfies the same partial differential equation (11) and the same boundary conditions (12) that the function
satisfies the same partial differential equation (11) and the same boundary conditions (12) that the function 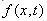
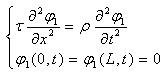
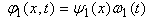 , one obtains for the function
, one obtains for the function 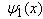 a selfadjoint boundary value problem
a selfadjoint boundary value problem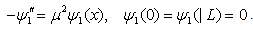
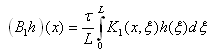
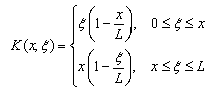
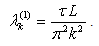
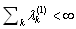 , the operator B1 belongs to the trace class. Normalized eigenvectors e(1)k of the operator B1 are given by
, the operator B1 belongs to the trace class. Normalized eigenvectors e(1)k of the operator B1 are given by
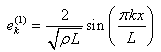 We select B2 in the same form as B1. Thus, the operator
We select B2 in the same form as B1. Thus, the operator  has eigenvalues
has eigenvalues
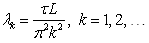 and each
and each  has multiplicity 2.Formula (7) gives
has multiplicity 2.Formula (7) gives
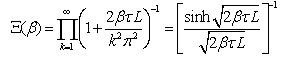 ,where we used the following well-known formula
,where we used the following well-known formula
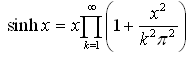 .Formula (8) gives
.Formula (8) gives
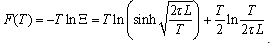 For entropy S one obtains using (9)
For entropy S one obtains using (9)
 and for heat capacity c using (10)
and for heat capacity c using (10)
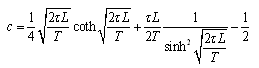 Note that
Note that 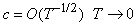 . as
. as Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML