-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Composite Materials
p-ISSN: 2166-479X e-ISSN: 2166-4919
2013; 3(3): 46-55
doi:10.5923/j.cmaterials.20130303.02
Hygro-Thermal Effects on Stress Analysis of Tapered Laminated Composite Beam
Debabrata Gayen, Tarapada Roy
Department of Mechanical Engineering, National Institute of Technology Rourkela, Rourkela, 769008, India
Correspondence to: Tarapada Roy, Department of Mechanical Engineering, National Institute of Technology Rourkela, Rourkela, 769008, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The present work deals with an analytical method in order to determine the stress distributions (such as axial in-plane stresses and inter-laminar shear stresses) in multilayered symmetric and anti-symmetric circular tapered laminated composite beams under hygro and thermal loadings. In the present analysis, all derivations for calculation of stresses have been developed based on the modification of conventional lamination and parallel axis theories. The hygro-thermal loads are considered as a linear function of coordinates in the planes of each layer. Hygro-thermally induced stresses are obtained for various types of laminates with cantilevered boundary conditions at different moisture concentrations and temperatures. A complete code has been developed using MATLAB program and validation of the present formulationshas been done by comparison with available solutions in the literature. Various results have also been found for tapered laminated cantilever beams of carbon/epoxy and graphite/epoxy materials. It has been observed that effects of stacking sequence, fiber orientation, coefficient of thermal expansion (CTE) and coefficient of moisture expansion (CME) have significance roles in the change of inter-laminar shear and axial in-plane stresses distribution through the laminate thickness.
Keywords: Tapered laminated composite, Conventional lamination theory, laminated plate approach, Inter-laminar shear stresses, axial in-plane stresses, Hygro-thermal load
Cite this paper: Debabrata Gayen, Tarapada Roy, Hygro-Thermal Effects on Stress Analysis of Tapered Laminated Composite Beam, International Journal of Composite Materials, Vol. 3 No. 3, 2013, pp. 46-55. doi: 10.5923/j.cmaterials.20130303.02.
Article Outline
1. Introduction
- Laminated composite structures/systems are increasingly used in aerospace and other engineering applications due to their high specific strength, stiffnessand good corrosion resistance, low coefficients of thermal expansion and of hygro-thermal expansion. They are subjected to different environmental conditions during service life. It has been seen that moisture and temperature have an adverse effect on the performance of composites (viz. stiffness and strength are reduced with the increase in moisture concentration and temperature). Although due to thermal expansion mismatch between layers of different fiber orientations, thermal stresses induced within and between laminas and thermal behaviors of the laminated composite material sare more pronounced than that of isotropic materials. Accurate evaluation of bending stiffness is an important for better prediction of axial in-plane stresses, inter-laminar shear stresses and deflection, bulking and vibration responses of structures. Some of the important works in the directions are presented in the following paragraph.Whitney and Ashton[1] considered the effect of environment on the bending of symmetric and un-symmetric laminated composite plates. Pipes et al.[2] analyzed the stresses in laminated composite plates subjected to the combined effect of elevated temperature and absorbed moisture. Sims and Wilson[3] derived an approximate elasticity solution for the transverse shearing stresses in a multilayered anisotropic composite beam. Sai Ram and Sinha[4] presented the effects of moisture and temperature on the bending characteristics of laminated composite plates using finite element method (FEM). Sai Ram and Sinha[5] investigated the effects of moisture and temperature on the free vibration of laminated composite plates.Sai Ram and Sinha [6]also investigated the effect of moisture and temperature on the buckling analysis of laminated composite plates. Chanand Demirhan[7] developed two analytical closed-form solutions, such as laminated plate approach and laminated shell approach, to evaluate the stiffness matrices and bending stiffness of the laminated composite circular tube. Tarn and Wang[8] presented a state space approach for the analysis of extension, torsion, bending, shearing and pressuring of laminated composite tube. Patel et al.[9] presented the static and dynamic characteristics of thick composite laminates exposed to hygro-thermal environments using eight-nodded C0 isoparametric higher order quadrilateral plate elements. Zenkour[10] investigated the static thermo-elastic response of symmetric and anti-symmetric cross-ply laminated plates considering unified shear deformation plate theory. Naidu and Sinha[11] analyzed the large deflection bending behaviour of laminated composite cylindrical shell panels subjected to hygro-thermal environments using FEM. Wang et al.[12] studiedhygro-thermal effect on the response of dynamic inter-laminar stresses distribution in laminated plates with piezoelectric actuator layers. Naidu and Sinha[13] analyzed free vibration behaviour of laminated composite shell subjected to hygro-thermal environments using FEM. Bahrami and Nosier[14] employed the displacement fields of general cross-ply, symmetric, and anti-symmetric angle-ply laminates under thermal and hygroscopic loadings and developed elasticity based solution for predicting the inter-laminar normal and shear stress distributions. Su[15] developed closed-form analytical solutions for evaluating the thermal induced stresses in laminated composite tubular and rectangular beams. Rao[16] developed closed-form expressions based on modifying the laminated plate approach to determine the displacement and twisting angle of tapered composite tube under axial tension and torsion. Shao and Ma[17] carried out the thermo-mechanical analysis of functionally graded hollow circular cylinders subjected to mechanical loads and linearly increasing boundary temperature. Syed et al.[18]presented the analytical expressions for computing thermal stresses in fiber reinforced composite beam with rectangular and hat sections under uniform temperature environment. Zenkour[19] studied the hygro-thermal bending analysis of functionally graded plate resting on elastic foundations. Singh and Chakrabarti[20] carried out hygro-thermal analysis of laminated composite plates using an efficient higher order shear deformation theory. Here plate model implemented with a computationally efficient C0 finite element using consistent strain field.Although literature review revealed that a lot of research work has been done on the inter-laminar shear stresses distribution and axial in-plane stress distribution analysis of laminated composite structures and also it is still remain as important area on research. In the present work a tapered laminated composite beam model has been considered and the details analysis has been carried out under bothhygro and thermal loadings.
2. Hygro-Thermo-Mechanical Analysis of a Tapered Laminated Composite Beam
- In the present model, the cross-sectional plane of the beam remains plane after deformation.
2.1. Geometry of Tapered Laminated Composite Beam
- A tapered laminated composite beam is considered with larger end radius
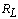 , smaller end radius
, smaller end radius 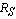 , Length L and a beam thickness t as shown in Fig. 1.The radius of the tapered beam at a distance x from the larger end,
, Length L and a beam thickness t as shown in Fig. 1.The radius of the tapered beam at a distance x from the larger end, 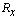 will be expressed as
will be expressed as 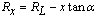 . Where α is the taper angle of the beam and
. Where α is the taper angle of the beam and 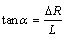 and difference between the large and small radii of the beam is
and difference between the large and small radii of the beam is 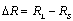 .
.2.2. Laminated Constitutive Equation
- Composite laminate consists of a set of multiple layers stacking together with different fiber orientations. It is very importance to analyze this problem based on layer by layer analysis. To circumvent or encompass this tedious approach, the laminate is often analyzed based upon its mid-plane axes as a reference axis. The properties of each layer are transformed to the reference axis. Now the general load-deformation relation of laminate composite is given as
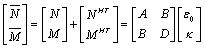 | (1) |
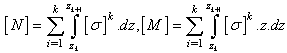 | (2) |
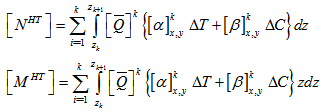 | (3) |
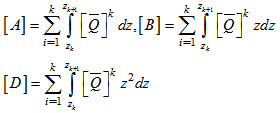 | (4) |
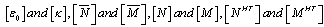 matrices are mid-plane strain and curvature, net resultant forces and moments, applied load and moment, hygro-thermal induced force and moment respectively.
matrices are mid-plane strain and curvature, net resultant forces and moments, applied load and moment, hygro-thermal induced force and moment respectively.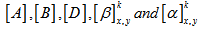 matrices are in-plane or extensional stiffness, extensional-bending coupling stiffness, bending stiffness, coefficient of thermal expansion (CTE) and coefficient of moisture expansion (CME)of
matrices are in-plane or extensional stiffness, extensional-bending coupling stiffness, bending stiffness, coefficient of thermal expansion (CTE) and coefficient of moisture expansion (CME)of 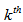 ply in the laminate x-y coordinate system. Now
ply in the laminate x-y coordinate system. Now 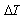 and
and 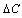 are the change of temperature and moisture concentration respectively. Here,
are the change of temperature and moisture concentration respectively. Here, 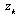 and
and 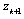 are the inner and outer coordinate of the
are the inner and outer coordinate of the 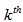 ply respectively.Now, constitutive (i.e. stress-strain) relation for a lamina in the principal material directions are presented as follows,
ply respectively.Now, constitutive (i.e. stress-strain) relation for a lamina in the principal material directions are presented as follows,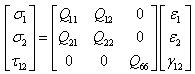 | (5) |
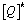 for
for 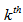 ply defined as,
ply defined as,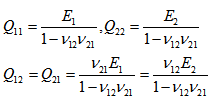 | (6) |
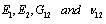 are the elastic moduli along longitudinal, transverse direction, shear modulus in 1-2 planes and Poisson’s ratio along the principal material directionrespectively.
are the elastic moduli along longitudinal, transverse direction, shear modulus in 1-2 planes and Poisson’s ratio along the principal material directionrespectively.2.3. In-Plane Stress Calculation
- For hygro-thermal stress analysis of tapered laminated composite beam, laminated plate approach is chosen due to its simplicity. Laminated plate approach is derived based on the conventional lamination theory and translation of laminate axis. Here infinitesimal element, which is inclined an angle θ with respect to the axis of the beam, z is rotated about the x axis as shown in Fig. 1.The total extensional, coupling and bending stiffness matrices of an
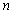 ply laminate with a ply thickness
ply laminate with a ply thickness 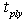 and mid-thickness radius of the tapered tube at a distance x from the larger end,
and mid-thickness radius of the tapered tube at a distance x from the larger end, 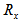 are obtained as follow
are obtained as follow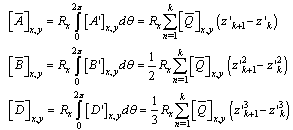 | (7) |
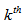 ply
ply 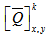 is given in appendix.
is given in appendix. 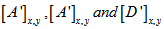 can be found out by parallel axis theorem and these can be written
can be found out by parallel axis theorem and these can be written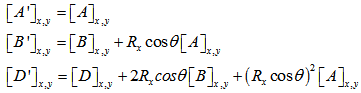 | (8) |
2.4. Determination of Hygro-thermal Force and Moment
- For finding the hygro-thermal force and moment expression the following steps are followed. In x-y coordinate system, CTE i.e.
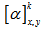 andCME i.e.
andCME i.e. 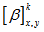 of
of 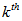 ply of the composite beam are obtained from the trans formation of CTE and CME of the lamina in 1-2 coordinate. Now from Fig. 1, these are first rotated about the x axis with an angle θ, rotated about z axis with the angle of fiber orientation
ply of the composite beam are obtained from the trans formation of CTE and CME of the lamina in 1-2 coordinate. Now from Fig. 1, these are first rotated about the x axis with an angle θ, rotated about z axis with the angle of fiber orientation 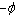 . So the transformation of CTE and CME in x-y coordinatesystem can be written as,
. So the transformation of CTE and CME in x-y coordinatesystem can be written as,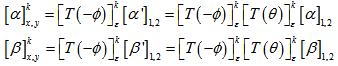 | (9) |
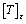 is given in appendix. The hygro-thermal induced force and moment are obtained by integrating thermal strain through the thickness of lamina, and can be expressed as,
is given in appendix. The hygro-thermal induced force and moment are obtained by integrating thermal strain through the thickness of lamina, and can be expressed as,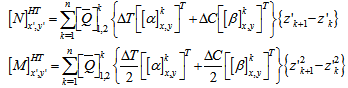 | (10) |
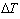 and
and 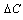 are the difference of temperature and moisture content respectively. The forces and moments of the mid plane of the lamina obtained using equation (10) can be transformed as,
are the difference of temperature and moisture content respectively. The forces and moments of the mid plane of the lamina obtained using equation (10) can be transformed as,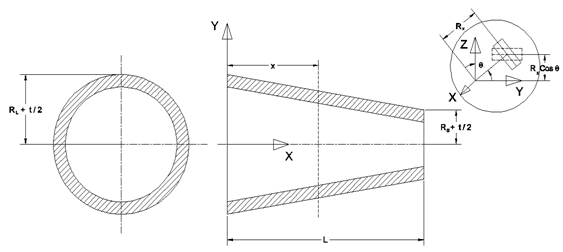 | Figure 1. Geometry of the tapered laminated composite beam |
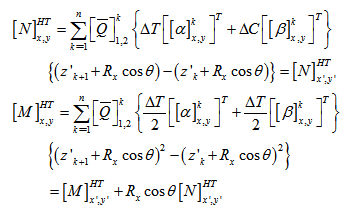 | (11) |
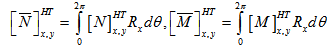 | (12) |
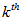 ply of the laminate can be obtained by using the following relations
ply of the laminate can be obtained by using the following relations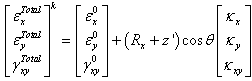 | (13) |
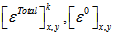 and
and 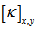 represent the total ply strain, mid-plane strain and mid-plane curvature respectively. The mechanical strain is obtained by subtracting the thermal strain from the total strain. Finally, the ply stress can be obtained by multiplying the matrix of the ply with the mechanical strain. It can be expressed as,
represent the total ply strain, mid-plane strain and mid-plane curvature respectively. The mechanical strain is obtained by subtracting the thermal strain from the total strain. Finally, the ply stress can be obtained by multiplying the matrix of the ply with the mechanical strain. It can be expressed as,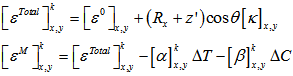 | (14) |
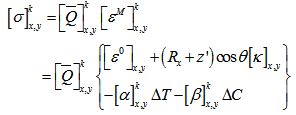 | (15) |
2.5. Inter-laminar Shear Stress Formulation under Transverse Load
- Sims and Wilson[3] developed an analytical solution of the inter-laminar shear stresses of the laminated composite beam subjected to a transverse load q. For analytical solution, two assumptions are made in derivation and these are, stresses not depend on y direction and
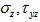 are small and can be neglected. So, the equationsat equilibrium for the
are small and can be neglected. So, the equationsat equilibrium for the 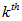 layer of the laminate can be written as,
layer of the laminate can be written as, 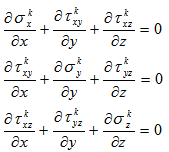 | (16) |
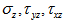 are assumed to be zero). Therefore, for finding the inter-laminar stress components beam is consider as narrow, so the stresses are assumed to be independent of y. For multi-layer laminate with
are assumed to be zero). Therefore, for finding the inter-laminar stress components beam is consider as narrow, so the stresses are assumed to be independent of y. For multi-layer laminate with 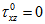 , above equation (16) can be reduced as,
, above equation (16) can be reduced as,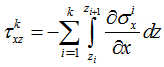 | (17) |
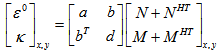 | (18) |
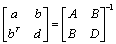 Hence, in the present analysis tapered cantilever beam is considered as a narrow beam, q is the transverse shear load per unit width and the in-plane forces are not considered on beam. So,
Hence, in the present analysis tapered cantilever beam is considered as a narrow beam, q is the transverse shear load per unit width and the in-plane forces are not considered on beam. So, 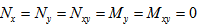 and
and 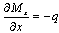 .After putting the equations (15) and (18) into equation (17), obtained the following expression
.After putting the equations (15) and (18) into equation (17), obtained the following expression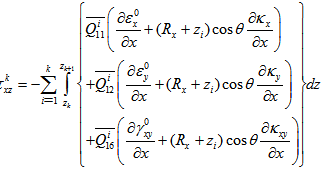 | (19) |
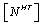 and
and 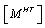 not depend on x, hence, equation (19) becomes,
not depend on x, hence, equation (19) becomes,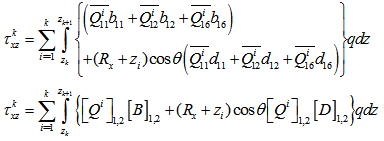
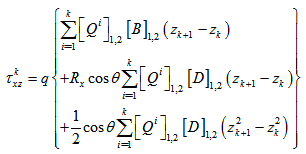 | (20) |
3. Results and Discussion
- The present analysis has been discussed based on the axial in-plane and inter-laminar shear stresses distribution of tapered laminated cantilever beam subjected to different combination of moistures and temperatures. Based on the above formulations a complete MATLAB code has been developed and validated. Various results for different fiber orientations and stacking sequences (viz. symmetric and anti-symmetric laminates) havealso been obtained and presented in the following subsections.
3.1. Validation of Developed MATLAB Code
- In order to verify the developed code the dimensions and mechanical properties considered for carbon/epoxy (AS4/3501-6) rectangular laminated cantilever beamare presented in[15].Fig. 2 shows the inter-laminar shear stresses distribution of this beam under thermal environment. It has been observed that result from the present code is excellent agreement with the already published results of Su[15] in case of thermal loading.
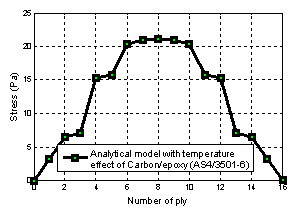 | Figure 2. Inter-laminar shear stress distribution for beam |
 .The variations of inter-laminar shear stresses across the thickness of thetapered circulargraphite/epoxy beam at different cross sections are depicted in Fig. 3.It is clearly observed from Fig. 3 that the inter-laminar stresses have a significant effect on the cross sections of tapered composite beam.
.The variations of inter-laminar shear stresses across the thickness of thetapered circulargraphite/epoxy beam at different cross sections are depicted in Fig. 3.It is clearly observed from Fig. 3 that the inter-laminar stresses have a significant effect on the cross sections of tapered composite beam. 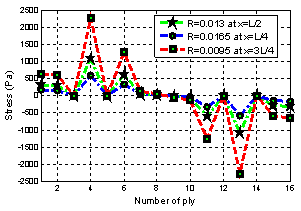 | Figure 3. Interlaminar shear stress distribution of tapered beam |
 | Figure 4. Normalized 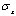 stress distribution of tapered beam stress distribution of tapered beam |
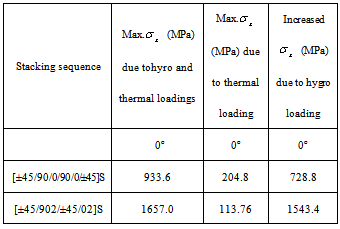
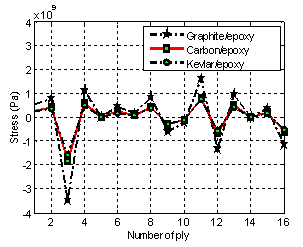
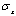 ) of tapered beam having different types of stacking sequences with tply=0.001321m, R=0.0130m,delT=325K and delC=1. It is clearly observed that the induced stress is more in case of anti-symmetric laminate. The comparison of increased stress in 0o ply due to hygro-thermal loading is presented in Table 1. From the Table 1, it is observed that the fiber orientation of the tapered laminated beam plays an important role in the variations of hygro-thermal induced stresses and it is also cleared that the constituent of0° and90° plies demonstrates the greatest significant due to hygo-thermal effect.
) of tapered beam having different types of stacking sequences with tply=0.001321m, R=0.0130m,delT=325K and delC=1. It is clearly observed that the induced stress is more in case of anti-symmetric laminate. The comparison of increased stress in 0o ply due to hygro-thermal loading is presented in Table 1. From the Table 1, it is observed that the fiber orientation of the tapered laminated beam plays an important role in the variations of hygro-thermal induced stresses and it is also cleared that the constituent of0° and90° plies demonstrates the greatest significant due to hygo-thermal effect.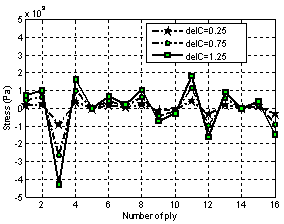 | Figure 5. Normalized 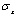 stress distribution with different moisture concentrations and Constant temperature stress distribution with different moisture concentrations and Constant temperature |
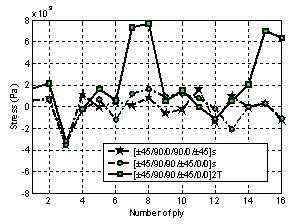 | Figure 6. Normalized 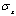 distribution for different stacking sequences for graphite/epoxy tapered beam distribution for different stacking sequences for graphite/epoxy tapered beam |
|
4. Conclusions
- An analytical method has been modified in order to predict the stress distribution within the layers and interfaces ofcircular tapered laminated beam under distributed, hygro and thermal loadings. From the present study, the following important conclusions may be madea) The axial in-plane stresses increases with the increases of moisture concentrations and temperatures.b) The combinations of different moisture concentrations and constant temperature have a significant effect on the axial in-plane stresses compared to the combination of different temperatures and constant moisture concentration. c) The fiber orientation of the plies plays an important role on the hygro-thermally induced axial in-plane stresses. This is mainly caused by the hygro-thermal induced moments which occur due to the mismatch of coefficients of axial thermal expansion and moisture expansion in each ply of the laminate
APPENDIX
- Transformations of Stiffness MatrixStress and Strain Transformation Matrices:For plane stress condition, 2D stress and Strain transformation matrix rotated a positive angle θ about x-axis can be written as,
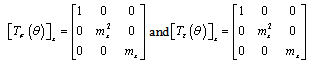 For plane stress condition, the 2D stress transformation matrix rotated a positive angle
For plane stress condition, the 2D stress transformation matrix rotated a positive angle 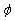 about z-axis can be obtained as,
about z-axis can be obtained as, Where,
Where,  and
and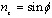 .Now, general transformation equation of stiffness matrix from material to laminate coordinate system can be written as,
.Now, general transformation equation of stiffness matrix from material to laminate coordinate system can be written as, 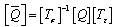 Where,
Where, 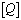 and
and are the reduced stiffness matrices of lamina which represent the stress/strain relationship with respect to material (1-2) coordinate system and laminate (x-y) coordinate system, respectively.Transformation of CTE and CME:
are the reduced stiffness matrices of lamina which represent the stress/strain relationship with respect to material (1-2) coordinate system and laminate (x-y) coordinate system, respectively.Transformation of CTE and CME: 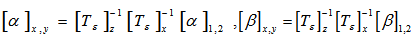
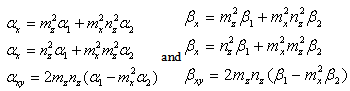 Transformation of stiffness matrix for the lamina that first rotated θ about x-axis, then about
Transformation of stiffness matrix for the lamina that first rotated θ about x-axis, then about 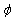 about z-axis can be written as,
about z-axis can be written as, 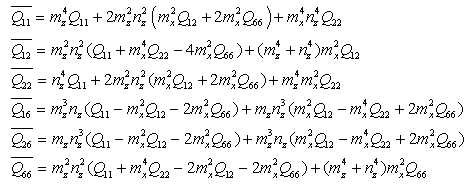 Total Extensional, Coupling and Bending Stiffness Matrices are,
Total Extensional, Coupling and Bending Stiffness Matrices are,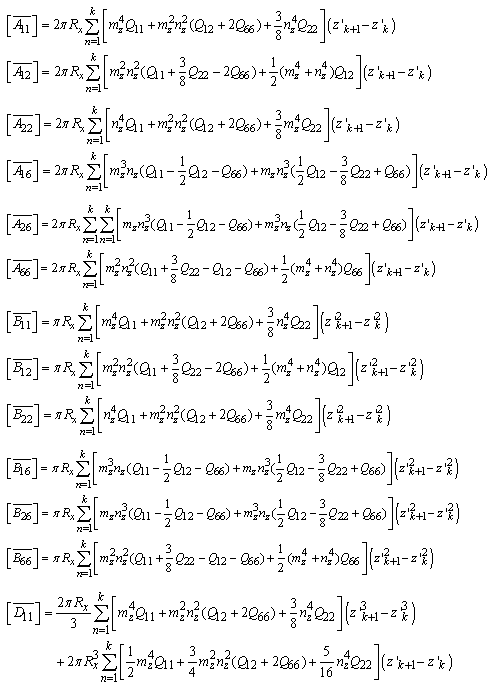
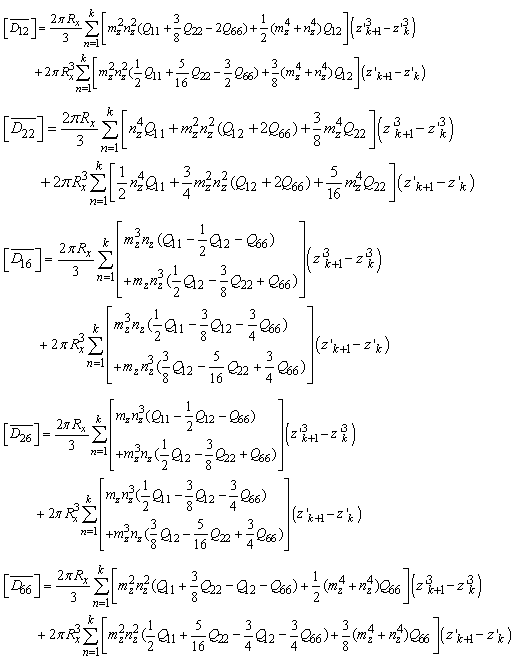 Overall Hygro-Thermal Induced Force and Moment of the tapered Beam:
Overall Hygro-Thermal Induced Force and Moment of the tapered Beam: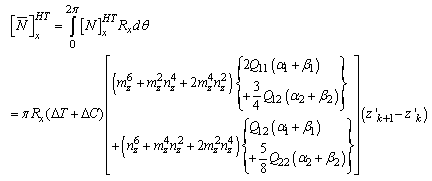

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML