1. Introduction

Understanding the relationship between structure and properties of matter, understanding of the structure as a model description, which sets the order in the distribution of characteristics values and the law of their evolution[1, 2], can, depending on the task, to focus attention on certain features of the material and neutralize the other. The models considered in this paper, describe the properties of resulting in the first place, the structure of the intermediate asymptotic[3]: in this case come to the fore a cluster component of the material and its internal boundaries (IB) – attribute components of the structure of the mesoscopic scale[3-6].

An internal boundary of the material is a fractal surface [4], separating different substances or different phases of one substance, or passing on material defects[7]. (Note that sometimes the internal boundaries are considered in the absence of heterogeneity or qualitative differences.Consider, as an example, the Earth's equator as the boundary between the upper and lower hemispheres of homogeneous sphere, and if allowed zero-dimensional boundaries, then the North Pole, and the centre of gravity, etc.[8]).

The inclusion of IB in the structural parameters of the material has several aspects. First, the IB are the inevitable result disproportionate and macroscopic structural units; second, the material is a complex system and, therefore, must have internal boundaries[9, 10].

Research connected domains such as interior boundaries, using the methods of percolation theory[3, 4] is a relevant for nearly half a century. In such problems, both physical body cluster systems and their influence on the object as a whole are studied. Interest in the percolation clusters (PC) of the particles and the internal boundaries of the material can be easily explained. PC substantially alter the processes of conduction, lead to the anomalous diffusion, determine the mechanical strength and corrosion resistance, impact on longevity, and other physical, chemical and mechanical properties. In addition, near the structural phase transition due to the large size of the clusters, their geometry does not actually depend on the substance, and has universal properties[3, 4, 6].

In spite of the great influence of the IB on properties of materials, was not studied the process of simultaneous forming of two cluster systems – clusters of particles and clusters of IB. The other two models presented in the article, describe some aspects of the force interaction of the clusters IB.

2. Percolation Model of Composite Structure

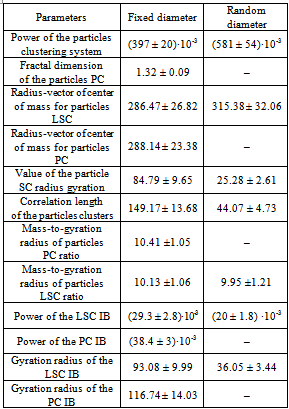
The increase of concentrations of material subsystems certain elements in the stochastic process of its genesis and evolution leads to initiation of a connected region of a certain phase (PC), which penetrates the physical body. This causes a qualitative leap in the development of the structure – the implementation of the structural phase transitions[3, 4, 11, 12]. One of the characteristic dimensions of the percolation cluster at the transition becomes comparable to the dimensions of the physical body. This leads to an abrupt change of the correlation length in the material, the appearance of a preferred direction and the lowering of the symmetry of the object. Thus, the percolation cluster, which sometimes takes a fraction of one percent of the body[13], do not just change some of its physical and chemical parameters, but in essence, defines the new state of matter[14].

The model is solved continuum percolation problem. Simulation of cluster formation processes is carried out on a square field of size 370×370 standard units of length, the elements of a percolation cluster – circle whose diameter is in the process of model experiment is fixed, or chosen from a set of values having a normal distribution. Control parameters of the model are the ratio between the diameter of the particles and the side of the field, as well as between the sizes of the particles forming the clusters. In model experiments, generally, the side of the square of the field is 40-50 times greater than the diameters of the particles. The coordination spheres consistent increase has been selected as the algorithm of cluster growth. Random Number Generation (RNG) with a uniform distribution[15] plays an important role in this process. The coordinates of cluster centers are selected using RNG, then – one of the centers, which will be another act of filling, and, finally, the generation indicates a place in the filled area, which be located next part of the growing cluster. RNG determines the specific value of the particle size, which are in the given interval.

The model clusters in the process of growth reach the size where ordinary particles can no longer be attached. The distance between the clusters at the same time becomes comparable to the particle diameter. This feature, as well as the fact that the geometry of the structures do not allow a new particle to lie on the plane, gives rise to the surface of the gaps and ways of arbitrary shape and size (Figure 1). This approach is actually formed by two cluster systems – the particle and the internal boundaries, which are the background for each other, as in mosaic by M. Escher. (In contrast to the "white" and "black" clusters, discussed in [11], IB forms the PC, which belongs to the known class of percolation theory problems with a zero threshold[13]).

The result of model calculations for PC and largest of small cluster (LSC) are presented in Tables 1 and 2. Tables demonstrate of the model capabilities: presented the calculated parameter and theirs accuracy. These findings – the result of statistical processing of the two types of computer experiments. In the first experiment, according to the previously described algorithm, increase the cluster of circles of fixed diameter around the centre of a random clustering was carried out. In the second experiment, the diameter was chosen with the help RNG with uniform distribution. Statistical sampling was done from Gaussian set of diameters, the largest of which is equal to the diameter from the experiment with the same circles. The dashes in the right column in Table 1 are typical: the onsets of clusters are extremely rare in such a setting of plane percolation problem, his absence is typically.

Two-dimensional problem is easily generalized to three dimensions. The volume problem is implemented in a cube containing 10⁶ cells. The typical implementation of the cluster structures in three-dimensional model: percolation clusters of spheres and internal boundaries (for clarity, in an empty field) are shown in Figure 2.

Figure 1. Cluster systems created from a set of equal particles (A) and particles with a normal size distribution (B)

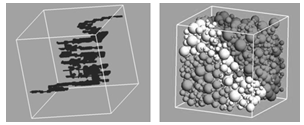Figure 2. The cluster system of internal boundaries and spheres in three-dimensional model

Table 1. Characteristic Parameters of a Particles Clusters and Internal Boundaries in the Two-Dimensional Model

Table 2. Characteristic Parameters of a Particles Clusters and Internal Boundaries in the Three-Dimensional Model Parameters Fixeddiameter Randomdiameter Particles clusteringsystem power (440 ± 50)∙10-3 (636.9 ± 59)∙10-3 Particles PC fractaldimension 1.49 ± 0.14 1.39 ± 0.12 Radius vector of the LSC center of mass 39.34 ± 4.03 36.86 ± 3.83 Radius vector of the PC center of mass 40.73 ± 4.48 51.57 ± 5.34 Value of the SC radius gyration 20.42 ± 2.44 12.61 ± 1.25 SC correlation length 38.58 ± 3.72 24.39 ± 2.24 LSC degree of anisotropy Axy 5.57 ± 0.73 3.89 ± 0.41 LSC degree of anisotropy Axz 5.42 ± 0.69 4.31 ± 0.19 LSC degree of anisotropy Ayz 26.41 ± 1.80 1.93 ± 0.10 PC degree of anisotropy Axy 10.64 ± 1.43 10.02 ± 1.35 PC degree of anisotropy Axz 20.73 ± 1.71 26.39 ± 3.25 PC degree of anisotropy Ayz 4.89 ± 0.65 4.86 ± 0.62 LSC IB power (900 ± 100)∙10-6 (400 ± 40)∙10-6 PC IB power (2600 ± 200)∙10-6 (800 ± 60)∙10-6 LSC IB gyration radius 19.43 ± 1.99 21.28 ± 2.37 PC IB gyration radius 29.49 ± 3.45 29.63 ± 1.66

3. Model of the Force Field of the Modified Sierpinski Square

Conditions of homogeneity violation arise spontaneously in various parts of the body. Qualitatively new evolution stage of the material occurs when degree of heterogeneity increase, and there are enough collective effects. The coherent interaction between the elements of the proportionate structure (a one scale level heterogeneity) leads to configurations that act as the initial elements for higher-level structure. This provokes the inflation of structure, and thus promotes the growth the texture material inhomogeneity, leads to the hierarchical subordination, and as a consequence, to the generation of fundamentally different structures. Material and internal borders are interdependent and jointly developing cluster systems. Internal borders evolve due to redistribution of deformation in material, changing the characteristic dimensions and learning new scales, thus, modifying the material.

It is known that deformation fields essentially depend on the configuration of the inhomogeneities. In the case of quasi-linear internal borders, (we are interested in primarily), the values of the strain tensor components are proportional to r ^–1[16], and, hence, their effect can be substantial at relatively large distances well above the interatomic. Orientation of the linear inhomogeneities occurring at the early stage of the material formation, of course, are not accidental, but ere not correlated.

Preferential direction in the orientation of newly formed linear irregularities occurs with increasing of their density. The deformation field activates the generation of parallel and hinders their growth in the perpendicular direction to the least extent. Thus, the linear growth of inhomogeneities occurs predominantly in two perpendicular directions, and there occurs a characteristic pattern in the distribution of equi-scale cracks. This aggravates the anisotropy, leads to a self-affine multifractal pattern of cracks and internal borders. A simple analogy to the plane and in the volume can be modified using affine maps such as other fractal Sierpinski carpet (square), Menger sponge, and their complements, respectively, as well as other suitable form of fractals[4, 17].

Consider the modified Sierpinski carpet, modeling the structure of the IB, with preferential direction (Fig. 3).

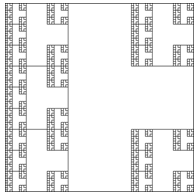Figure 3. Modified Sierpinski carpet with mirror symmetry

We consider a “wire” model of the Sierpinski carpet. Let the initial square frame be divided by four wires into nine equal squares. The procedure is repeated many times on each of the 5^m frames that are constructed in the subsequent step (see Fig.3). We also assume that on each side of frames of an arbitrary “generation”, there are point sources distributed with a line density λ and generating a field with the strength E ~ 1/r². We find the analytic form of the force field generated by the multi-scale network of the internal edges of the Sierpinski square of an arbitrary subdivision step m.

We assume that the origin does not lie on any line containing edges of cells of the carpet of the m^th generation. Let the carpet center be at the point (ξ; η).

We set

E_x ≡ X_m (ξ; η), E_y ≡ Y_m (ξ; η),

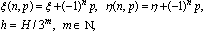A (u;v) = k λ /(u² + v²)^1/2 , B (u;v) = k λ v /u (u² + v²)^1/2,

where k is a coefficient depending on the selected set of units.

Then, the strength created by the carpet in the point with coordinates (x; y) is determined by the following recurrent relations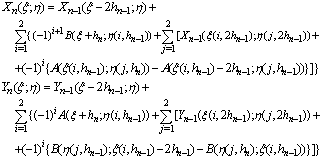

4. Oscillatory Interaction of Different Scale Structures

The force field of randomly located quasi-parallel linear inhomogeneities is a complex interference pattern. One of the possible mechanisms of interaction of structural inhomogeneities and exploration of their scales are also associated with the interference. When some of the material field of equi-scaled cracks add up to form a local area with the magnitude of deformation, exceeding the average value, it creates preconditions for the formation energy of larger linear inhomogeneity.

Statistical self-similarity in the location of the borders leads to some "multiplicity" in the configuration of fields, this mechanism is projected for all large scale, creating an increasingly large cracks and interfaces, covering a considerable space. In turn, the more powerful deformation fields of large linear inhomogeneities provoke their further growth by acting on smaller scale heterogeneity.

This occurs simultaneously at all scales, reveals interdependence and mutual influence of different levels of structural inhomogeneities, the existence of positive feedback and interaction between the oscillating linear inhomogeneities of different structural levels. Let us examine these processes as rapidly damped oscillatory solid-state reaction. Let the physical body is an oscillatory system in this sense. This is an autonomous distributed non-conservative system with damped anharmonic vibrations.

If we assume that the generalized force of resistance acting in the system which is proportional to the velocity of propagation of energy in the system between linear inhomogeneities of different scale levels, adjusted for the level of validity of assumptions, the equation of motion (in a linear approximation) will have a standard form

x″ + 2γx′ + ω² x = 0,where γ – the generalized damping coefficient, ω – cycling frequency. Let us estimate the conditional period T of these oscillations[18] for a system of linear irregularities cuboid. We introduce the inverse of the coefficient of rigidity of the body – compliance C = 1/k, which determines how far the scale of the process may spread to crack, and for which there is a calculation formula

C = 8a³/(E h³ b),where a – crack length, h – the distance from it to the edge of the body, b – thickness of the plate, E – Young’s modulus[19].

Assuming γ small, we have

ω² ≈ ω₀² = 1/(m•C),then

T = 4π (2 a³ m / E h³ b)^1/2,where m – mass of the body.

Another evaluation of the conditional period may be obtained by determining the logarithmic decrement a serial (with an interval of period) the energy values of W_n[18, 20]

T = (1/γ)•(W_n – W_{n + 1}) /(W_n + W_{n + 1}).

A possible application of the results obtained is the description of oscillatory interaction for multiscale internal boundaries in a heterogeneous material.

5. Conclusions

Understanding of the similarity of properties of particles and IB clusters, the ability to calculate their parameters and force interaction, can enhance the opportunities for influence on the design of materials.