-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Chemistry
p-ISSN: 2165-8749 e-ISSN: 2165-8781
2022; 12(3): 54-61
doi:10.5923/j.chemistry.20221203.02
Received: Aug. 10, 2022; Accepted: Aug. 28, 2022; Published: Aug. 30, 2022

Thermal Effects of Superfluid on Chemistry
Wei Chen
General Electric, 300 Garlington Rd, Greenville, South Carolina, USA
Correspondence to: Wei Chen, General Electric, 300 Garlington Rd, Greenville, South Carolina, USA.
| Email: |  |
Copyright © 2022 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Since the discovery of superfluids in the early 20th century, ballistic phenomena have also been observed in chemistry and biochemistry. They are unsolved problems and contradict modern thermodynamics. A recent study considers the superfluidity as the result of the isentropic state in dynamics, which has provided a solution for the superfluid and super heat transfer problems. Here, we demonstrated that the solution of the ballistic phenomenon leads to the revisions of the thermodynamic laws that chemistry relies on. We showed the comparison of superfluid experimental data to the theory. From the comparison, the calculations verify the new formulae of thermodynamic laws. The revised thermodynamic laws can be applied to both regular materials and supermaterials. In conclusion, the first law should include both the regular fluid and superfluid for conservation of mass, momentum and energy. In the second law, the entropy can be reduced by a superfluid under certain conditions, and with a superfluid, the efficiency of the thermodynamic cycle can be greater than that of the Carnot cycle. The Maxwell relations remain unchanged with superfluid. These findings should lay out the necessary foundation for solution ballistic chemical reactions, biochemical reactions, phase transitions and transport processes.
Keywords: Fountain effects, Isentropic motion, Super heat transfer, Second sound
Cite this paper: Wei Chen, Thermal Effects of Superfluid on Chemistry, American Journal of Chemistry, Vol. 12 No. 3, 2022, pp. 54-61. doi: 10.5923/j.chemistry.20221203.02.
Article Outline
1. Introduction
- Ballistic chemical reactions, ultra-high-rate biochemical reactions, instant phase transitions and sonic species transport are unsolved problems that are related to superfluidity. They share the same first principle challenges on thermodynamics. Modern thermodynamics is constructed on diffusion processes and does not include ballistic phenomena. In this manuscript, we demonstrate that with the presence of superfluid, the thermodynamic laws must be changed to include both the regular fluid and superfluid. By comparison to the experimental data, the shortcomings of the modern thermodynamic laws are discussed, and revisions are recommended.The discovery of superfluids is probably the most important achievement in the early 20th century [1] [2] [3]. In 1911, it was observed that electricity was conducted at nearly no resistance at low temperature, contradicting the belief that electricity would encounter infinite resistance [1]. Liquid helium II was found to have very high thermal conductivity [4] in 1936, very low molecular viscosity [2] in 1938, and second sound [5] in 1946, which was described by the so-called two-fluid model [6] [7] in 1941. Since superfluid was found at low temperatures, the phenomena were considered to happen with a superfluid with completely different, low-temperature properties. Since they are associated with high speed, these phenomena are often called ballistic transport and have been classified as particle physics or quantum behavior.Ballistic chemical reactions have been observed much later [8] [9] [10]. Since the reactants move ballistically, these kinds of chemical kinetics are named ballistic annihilation [8], particle-anitparticle annihilation [9] and fractal reaction [10]. The experiments on the reaction kinetics of excitations in molecular macro-clusters showed that the reactions are dependent on time by an “excitation-fusion” reaction, where both reactant and product are “radioactive” at a singlet excitation [11] [10]. A fast, biochemical effect has also been observed in the mutation rate of bacteria such as Escherichia coli [12], and they found that high mutation rates are a direct response to resource-replenishment cycles. Another biochemistry example is DNA tunneling [13] [14] [15]. In the DNA double helix, spontaneous mutations of so-called Watson-Crick-like geometry have been observed at an extremely fast rate under excitation [14].Recent developments in nanotechnology provide the means to examine, test and fabricate materials at the size of molecules [16] [17]. In addition to superfluid [18] [19] and super heat transfer [20] [21], super mass transfer [22] and super phase transitions [23] [24] [18] are observed, where ultrafast ice-phase flows across nanotubes at room temperature [18]. Closely related to the development of nanotechnology, nanochemistry has become particularly focused on the properties related to other abnormal observations, which may or may not be related to ballistic phenomena [25] [26].It is clear that the phenomena of superfluid cover almost all disciplines of science and engineering, not just physically at low temperatures. A recent study on superfluids shows that any dissipative motion has a counter nondissipative motion, which is superfluid [27]. In other words, a dissipative chemical reaction has its counter nondissipative reaction; a dissipative phase transition has a nondissipative phase transition, etc. Although this broad hypothesis has to be confirmed by an extraordinary amount of work, it is anticipated that if it is the case, we have to establish our existing thermodynamics with the superfluid in mind; otherwise, both experimental and theoretical work will be hindered by the lack of acknowledgement of the existence of superfluid.Here, we emphasize the importance of the thermal effects of superfluids on chemistry. In addition to the issues above, there are several issues with traditional thermochemistry. First, it has been noticed that the properties of chemical reactions become functions of time and excitation. Since the superfluid depends on the dynamics and when and how a fluid becomes isentropic, the behavior of the regular fluid is also greatly affected by dynamics. If the superfluid has not been properly taken care of, these properties will appear to be “odd” or “anomalous.” Second, the consequences of the anomalous properties will lower the reliability of large industrial equipment such as petroleum refinery plants, power plants [28] and transportation vehicles [29]. Third, without proper consideration of superfluids, the risks of damage and catastrophic events are much higher. For example, if a combustion system is excited and becomes local superfluid or a substantial portion of the combustion chamber becomes superfluid, the combustion will become much more rapid, and local overheating or flame flashback may occur.On the other hand, if we consider the superfluid properly, we not only solve the issues above but also benefit from higher efficiency and controllable chemical reactions. We can design chemical reactions such that they maximize the thermal and chemical performance.We believe that the thermodynamics of superfluids must be established to solve ballistic chemistry and ballistic biochemistry problems. The first law of thermodynamics is about conservation, i.e. mass, momentum and energy conservation. If we do not clarify the role of superfluids on the conservation laws, it is impossible to conclude a reliable experiment or theory. In modern thermodynamics, the second law sets up the limits of dissipative motion. There is already abundant evidence and experimental data that contradict the second law. For example, the thermal efficiency of a heat pipe or a superconducting vortex has already shown that the thermal efficiency is much higher than that of a Carnot cycle. The removal of this limitation from the second law allows practitioners to pursue the highest possible efficiency and quality, which will yield tremendous economic benefits. What we try to say is that the thermodynamics of superfluid is the foundation for all subjects of chemistry and biochemistry, and its solution has to take place to solve other problems associated with ballistic phenomena in chemistry and biochemistry.In this manuscript, we show that the thermal effects of superfluids are evident for the revision of thermodynamic laws through theoretical reasoning and experimental data comparison. We present the thermal effects of superfluids in three parts. First, we establish the mathematical formulae from the excess entropy theory [27] and compare the calculation with the experimental data. From the data comparisons, we develop the thermodynamic cycle with superfluid and calculate the thermal efficiency and entropy. We illustrated and reviewed the results that contradict modern thermodynamics. Second, we generalize the results to thermodynamic laws and propose revisions of those laws. Third, we conclude with the key findings and the revised thermodynamics. For convenience, we appended the derivations of superfluid and the formulae used in the calculation.
2. Motion of Liquid Helium in a Capillary
- In this section, we first develop formulae to calculate the flow and heat transfer of superfluids in a capillary. Then, we compare them with two experiments conducted by Kapitza [3]. After we validated the theory, we highlight the results that help to study thermodynamic laws in the next section.
2.1. Theory
- Liquid Helium II flow in a capillary can be schematically described by Figure 1. In Fig. 1, helium II flows into capillaries at velocity
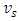 from the cold reservoir, and regular helium discharges at
from the cold reservoir, and regular helium discharges at 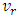 from the hot reservoir through the capillary tube. A thermal load
from the hot reservoir through the capillary tube. A thermal load 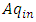 is exerted onto the hot reservoir, and A is the cross section of the capillary. The small oscillatory component drives helium into the superfluid, and when the frequency of load is in the vicinity of the natural frequency, resonance occurs. Usually, resonance is sustained for a short period as a steady state and then breaks down. Here, we are only interested in this steady-state period, where conservation is expressed by [27],
is exerted onto the hot reservoir, and A is the cross section of the capillary. The small oscillatory component drives helium into the superfluid, and when the frequency of load is in the vicinity of the natural frequency, resonance occurs. Usually, resonance is sustained for a short period as a steady state and then breaks down. Here, we are only interested in this steady-state period, where conservation is expressed by [27],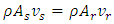 | (1) |
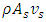 is the mass flow rate of the superfluid into the capillary, and
is the mass flow rate of the superfluid into the capillary, and 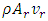 is the mass flow rate of the regular fluid out of the capillary.
is the mass flow rate of the regular fluid out of the capillary.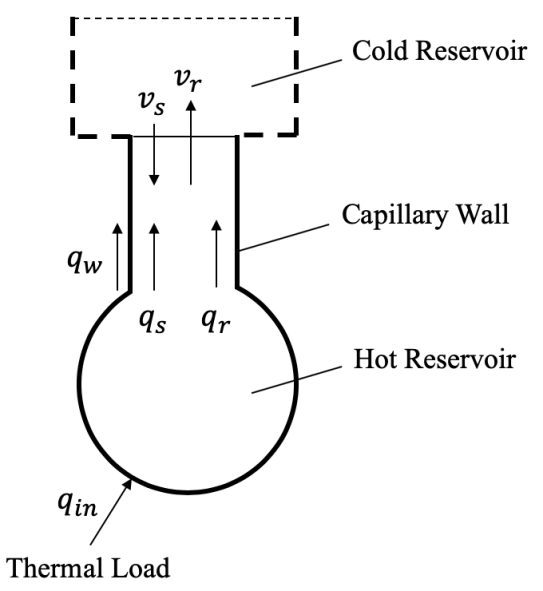 | Figure 1. Liquid Helium II in A Capillary |
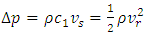 | (2) |
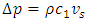 is the momentum of the superfluid at resonance given in Appendix (A.14).
is the momentum of the superfluid at resonance given in Appendix (A.14). 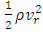 is the momentum of the regular fluid from the Bernoulli equation. At steady state, the energy conservation can be expressed by
is the momentum of the regular fluid from the Bernoulli equation. At steady state, the energy conservation can be expressed by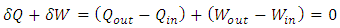 | (3) |
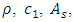 and
and 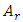 are the density and speed of the first sound of helium and the flow areas of superfluid and regular fluid, respectively.
are the density and speed of the first sound of helium and the flow areas of superfluid and regular fluid, respectively. 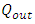 consists of sonic heat transfer through the wall and superfluid [27] and convection by regular fluid,
consists of sonic heat transfer through the wall and superfluid [27] and convection by regular fluid,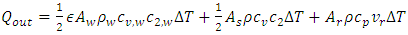 | (4) |
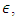 wall factor is a fraction of wall participating super heat transfer and 0.03 used throughout this manuscript.
wall factor is a fraction of wall participating super heat transfer and 0.03 used throughout this manuscript. 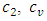 and
and 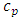 are the speed of the second sound and the isochoric and isobaric specific heat of liquid helium, respectively.
are the speed of the second sound and the isochoric and isobaric specific heat of liquid helium, respectively. 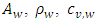 and
and 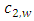 are the cross-sectional area, density, specific heat and speed of the second sound of the wall, respectively.
are the cross-sectional area, density, specific heat and speed of the second sound of the wall, respectively. 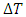 is the temperature difference between the hot and cold reservoirs. Both
is the temperature difference between the hot and cold reservoirs. Both 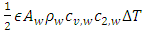 and
and 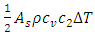 are from Appendix (A.15), and
are from Appendix (A.15), and 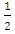 is from the impedances at both ends of the capillary. The kinetic energy
is from the impedances at both ends of the capillary. The kinetic energy  of the regular fluid jet is given
of the regular fluid jet is given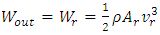 | (5) |
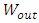 is the total kinetic energy of helium exiting the capillary. Since regular fluid is the reflection of superfluid, we only count one, not both. Before it enters the capillary, the superfluid is not subject to the first sound, and its kinetic energy is trivial. From (1) to (5), we obtain the working equation for the velocity of a regular fluid,
is the total kinetic energy of helium exiting the capillary. Since regular fluid is the reflection of superfluid, we only count one, not both. Before it enters the capillary, the superfluid is not subject to the first sound, and its kinetic energy is trivial. From (1) to (5), we obtain the working equation for the velocity of a regular fluid, 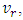
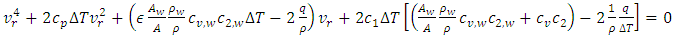 | (6) |
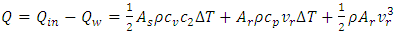 | (7) |
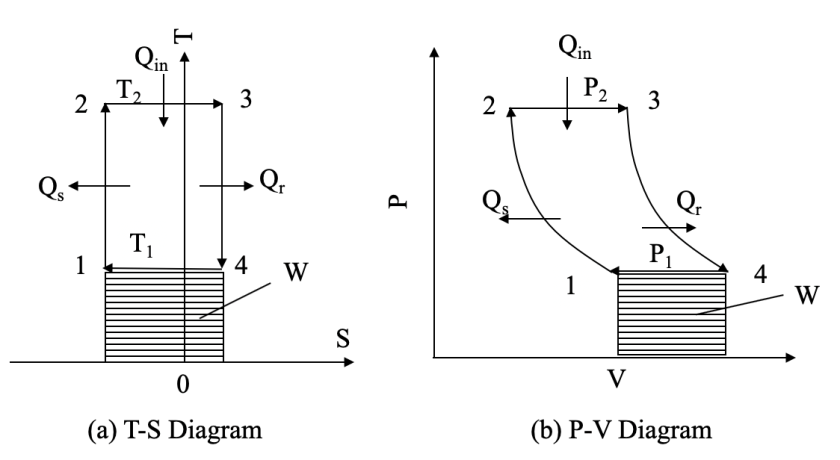 | Figure 2. A Cycle Diagram of Superfluid |
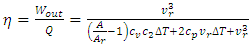 | (8) |
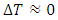 ,
, 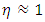 , a supervortex spontaneously forms [30]. The entropy contribution of the cycle can be calculated by
, a supervortex spontaneously forms [30]. The entropy contribution of the cycle can be calculated by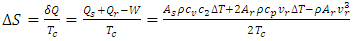 | (9) |
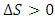 , the spontaneous process increases the entropy of the environment. Otherwise, it reduces entropy.
, the spontaneous process increases the entropy of the environment. Otherwise, it reduces entropy.2.2. Validation
- Now, we present two comparisons of the theory to experiments by Kapitza [3]. Overall, the theory agrees with all data reasonably well and under some conditions very well.The first apparatus had a 4 cm long capillary with a 0.61 mm inside diameter and a 1.21 mm outside diameter [3], as shown in Fig. 1. The cold reservoir was a tubular section on the top, and the hot reservoir had a cavity of 1 to 2 cm3 in volume equipped with Joule heating and a thermometer. We adopt the thermal mechanical properties of glass from [31] [27] to calculate the speed of the second sound and heat flux through the capillary wall. The thermal mechanical properties of regular helium fluid are from [32] except the thermal conductivity from [33].In Fig. 3, the cycle efficiency of the superfluid is above 90%, and the Carnot efficiency is approximately two orders of magnitude lower and undoubtedly small due to trivial temperature differences between hot and cold reservoirs. The Carnot efficiency being regarded as the maximum is due to entropy,
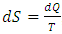 , where
, where 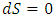 must result in
must result in 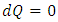 for dissipative fluid. For a superfluid,
for dissipative fluid. For a superfluid, 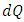 does not have to be zero at
does not have to be zero at 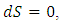 and heat transfer can occur isentropically. Therefore, the maximum from the Carnot cycle no longer holds.
and heat transfer can occur isentropically. Therefore, the maximum from the Carnot cycle no longer holds.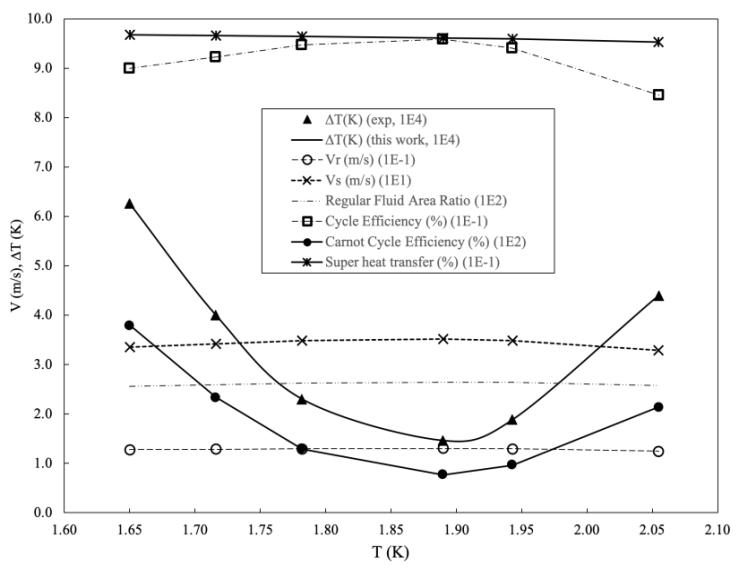 | Figure 3. Heat Transfer and Velocity in Stationary Capillary at load 0.45 W/cm^2 (Data from Fig. 2 in [3]) |
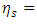
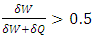 ,
, 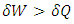 . From the second law, the contribution of entropy to the environment by the system can be calculated by
. From the second law, the contribution of entropy to the environment by the system can be calculated by 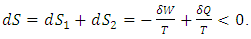 Thus, when superfluid is considered, a spontaneous process can reduce the entropy of the system.The next apparatus consisted of a stationary capillary, a vane, which was hung by a cross-bar on a quartz fiber. The horizontal, stationary capillary was 4 cm long and had an inside diameter of 0.4 mm, and the vane had three disks of 4, 2, and 1 mm diameter. The pressure of impingement by a helium jet is calculated by
Thus, when superfluid is considered, a spontaneous process can reduce the entropy of the system.The next apparatus consisted of a stationary capillary, a vane, which was hung by a cross-bar on a quartz fiber. The horizontal, stationary capillary was 4 cm long and had an inside diameter of 0.4 mm, and the vane had three disks of 4, 2, and 1 mm diameter. The pressure of impingement by a helium jet is calculated by 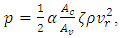 where
where 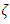 and
and 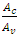 are the area ratios of a jet of regular fluid to capillary and capillary to vane.
are the area ratios of a jet of regular fluid to capillary and capillary to vane. 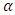 is the degradation factor of a jet. In Fig. 4, the calculated impinging pressures capture the essential trend of the experimental data for all temperatures and at 1.92 K and 2.11 K, the theory matches the measurements very well. Both experimental data and calculations show a peak impingement, although the calculation appears to be more pronounced. The peak is attributed to the competition of thermal load and super heat transfer.
is the degradation factor of a jet. In Fig. 4, the calculated impinging pressures capture the essential trend of the experimental data for all temperatures and at 1.92 K and 2.11 K, the theory matches the measurements very well. Both experimental data and calculations show a peak impingement, although the calculation appears to be more pronounced. The peak is attributed to the competition of thermal load and super heat transfer.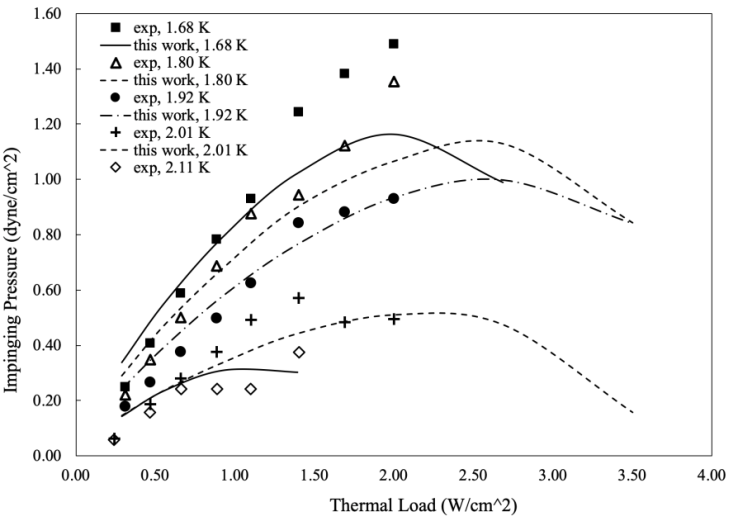 | Figure 4. Impinging Pressure from Jet in Capillary (Data from Fig. 11 in [3]). Degradation factor: 0.0184 at 1.68 K, 0.0158 at 1.80 K, 0.0131 at 1.92 K, 0.0078 at 2.01 K, 0.0078 at 2.11 K |
3. Generalized Thermodynamics
- In this section, we review modern thermodynamics from preceding theory and experiments. In particular, we pay attention to the first and second law and the Maxwell relations of thermodynamics.
3.1. First Law
- From (1), (2) and (3), it becomes clear that the conservation of a system with ballistic phenomena must include the quantities from superfluid. Here, we try to generalize (1), (2) and (3) by assuming energy
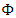 is a continuous and differentiable function, and the first law states
is a continuous and differentiable function, and the first law states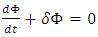 | (10) |
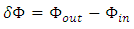 is the difference in cumulative total energy during an infinitesimal time difference
is the difference in cumulative total energy during an infinitesimal time difference 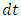 across the boundary and
across the boundary and 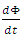 is the change in energy in the domain. The energy is defined by
is the change in energy in the domain. The energy is defined by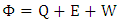 | (11) |
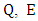 and
and 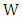 are thermal energy, internal energy and work, respectively, which can be further itemized by a regular fluid and superfluid as
are thermal energy, internal energy and work, respectively, which can be further itemized by a regular fluid and superfluid as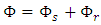 | (12) |
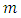 , and specific quantity,
, and specific quantity, 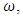 (12) becomes
(12) becomes 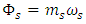 for superfluids and
for superfluids and 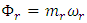 for regular fluids. To maintain (10), the following equivalence is required:
for regular fluids. To maintain (10), the following equivalence is required: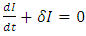 | (13) |
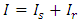 represents all constituents, such as mass, momentum, angular momentum and electrical charge. For example, for a steady superfluid stream, since
represents all constituents, such as mass, momentum, angular momentum and electrical charge. For example, for a steady superfluid stream, since 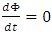 and
and 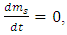 we obtain
we obtain 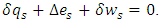 If we prefer the total differentiation, it becomes
If we prefer the total differentiation, it becomes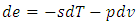 | (14) |
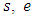 and
and 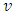 are the specific entropy, internal energy and volume, respectively.
are the specific entropy, internal energy and volume, respectively. 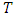 and p are temperature and pressure. Now, we obtain the differential form of internal energy for the superfluid in the first law.
and p are temperature and pressure. Now, we obtain the differential form of internal energy for the superfluid in the first law.3.2. Maxwell Relations
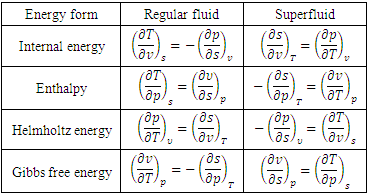
- The internal energy for a regular fluid is obtained from the total derivative by
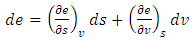 | (15) |
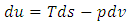 | (16) |
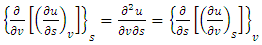 | (17) |
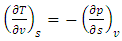 | (18) |
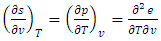 | (19) |
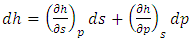 | (20) |
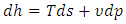 | (21) |
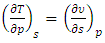 | (22) |
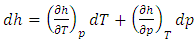 | (23) |
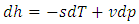 | (24) |
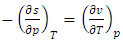 | (25) |
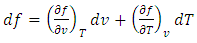 | (26) |
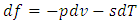 | (27) |
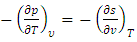 | (28) |
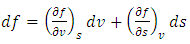 | (29) |
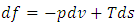 | (30) |
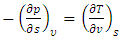 | (31) |
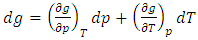 | (32) |
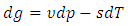 | (33) |
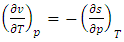 | (34) |
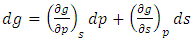 | (35) |
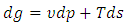 | (36) |
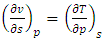 | (37) |
|
3.3. Second Law
- The second law from the Carnot theorem is simply that no engine operating between two given reservoirs can be more efficient than a Carnot engine operating between the same two reservoirs [34] [35]. In a closed system, the efficiency of a Carnot engine is determined by the temperatures of two reservoirs,
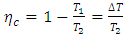 | (38) |
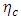 is the efficiency of the Carnot engine and
is the efficiency of the Carnot engine and 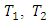 and
and 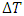 are the temperatures of the cold and hot reservoirs and the temperature difference between the hot and cold reservoirs. The thermodynamic system of the liquid helium flow in Figure 1 is a closed system, and its efficiency is given in (8), and its Carnot cycle efficiency can be calculated from the first validation case in Figure 3,
are the temperatures of the cold and hot reservoirs and the temperature difference between the hot and cold reservoirs. The thermodynamic system of the liquid helium flow in Figure 1 is a closed system, and its efficiency is given in (8), and its Carnot cycle efficiency can be calculated from the first validation case in Figure 3,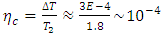 | (39) |
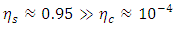 | (40) |
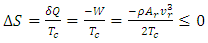 | (41) |
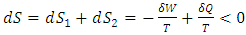 | (42) |
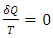 | (43) |
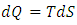 , which is the area covered by the vertical strip. On the other hand, in a superfluid process, heat release is defined by
, which is the area covered by the vertical strip. On the other hand, in a superfluid process, heat release is defined by 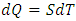 , which is the area covered by the horizontal strip in Fig. 2. Thus, the work done by the cycle is the shaded area in Fig. 2 from (3). From the first law (3) and (10),
, which is the area covered by the horizontal strip in Fig. 2. Thus, the work done by the cycle is the shaded area in Fig. 2 from (3). From the first law (3) and (10),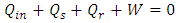 To maintain the sign of
To maintain the sign of 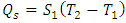 and
and 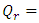
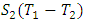 from the direction of processes in Fig. 2, we shall place the origin of the entropy at the middle somewhere to keep
from the direction of processes in Fig. 2, we shall place the origin of the entropy at the middle somewhere to keep 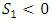 as in Fig. 2. It can be easily visualized that if the surrounding area is smaller than the shaded area, the thermal efficiency of a superfluid cycle is higher than that of the Carnot cycle. Since
as in Fig. 2. It can be easily visualized that if the surrounding area is smaller than the shaded area, the thermal efficiency of a superfluid cycle is higher than that of the Carnot cycle. Since 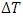 is usually very small in super heat transfer, the cycle efficiency of a superfluid is much higher than that of a Carnot cycle. Consequently, as we discussed with (9), the entropy production of a spontaneous superfluid cycle is negative when its thermal efficiency is greater than 50%, and the amount of contribution is the shaded area minus the area circled by the cycle.Philosophically, the argument has been made that the reliance of the second law on the notion of a heat engine, a thermal cycle and entropy may not be as precise as Caratheodory’s principle [34], which may limit our interpretation of the second law in general. Since the Carnot principle and the entropy interpretation of the second law have directly impact quantitatively on chemistry and biochemistry, we propose to change the modern interpretation and leave Caratheodory’s principle for further discussion.
is usually very small in super heat transfer, the cycle efficiency of a superfluid is much higher than that of a Carnot cycle. Consequently, as we discussed with (9), the entropy production of a spontaneous superfluid cycle is negative when its thermal efficiency is greater than 50%, and the amount of contribution is the shaded area minus the area circled by the cycle.Philosophically, the argument has been made that the reliance of the second law on the notion of a heat engine, a thermal cycle and entropy may not be as precise as Caratheodory’s principle [34], which may limit our interpretation of the second law in general. Since the Carnot principle and the entropy interpretation of the second law have directly impact quantitatively on chemistry and biochemistry, we propose to change the modern interpretation and leave Caratheodory’s principle for further discussion.4. Conclusions
- In this manuscript, we propose the revision of thermodynamic laws to include superfluids. Here, we use superfluids to represent all phenomena of the super state, such as ballistic chemical reactions, ballistic biochemical reactions and ultrafast phase transitions. In our definition, ballistic phenomena or super states occur isentropically under cyclic motions.(1) For the first law, conservation must include both superfluids and regular fluids simultaneously because the superfluids are regular fluids in an isentropic state and are dynamically interconverted. Without superfluid, the calculations of conservation will be erroneous, and the second law will be misrepresented.(2) For the second law, with superfluid, entropy can increase or decrease. Although it always increases for the motions of regular fluid only, the entropy of the system is determined dynamically. Because of the inclusion of superfluid, the Carnot cycle is not the limit of the efficiency of a general thermal cycle.(3) Under certain conditions, superfluids can spontaneously form a thermodynamic cycle with a regular fluid at very high thermal efficiency. A cycle diagram, similar to those for regular fluids, can be constructed for superfluid and regular fluid.(4) Maxwell relations remain unchanged for superfluids, which indicates that Maxwell relations describe only the nondissipative phenomena.Here, in this manuscript, we only focus on the thermal effects of superfluids on chemistry, biochemistry, phase transitions, etc. As a result, the thermodynamic laws have to be revised, which will affect the thermochemistry, the methods of calculations on conservation and the determination of accuracy of an experiment. It must be stressed that each ballistic phenomenon has to establish its own method to discern where and when it is in a regular state or a super state according to its own physics and chemistry, which is not covered in this manuscript.
Appendix
- In this appendix, we briefly present the key derivations and results from [27] for reader convenience.To illustrate how we determine if a motion is in the super state, we adopt the Navier-Stokes equations,
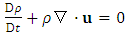 | (A.1) |
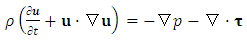 | (A.2) |
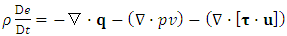 | (A.3) |
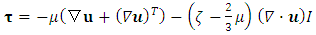 and
and 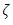 are the bulk viscosity,
are the bulk viscosity, 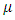 is the molecular viscosity and
is the molecular viscosity and 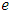 is the density of the internal energy.
is the density of the internal energy. 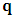 is the heat conduction,
is the heat conduction, 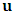 is the velocity,
is the velocity, 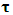 is the stress tensor,
is the stress tensor, 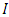 is a unit tensor and
is a unit tensor and 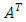 is the transpose of tensor
is the transpose of tensor 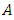 . Sometimes, it is more convenient to write the energy equation in entropy [36] [37] [38] or temperature [36] form as follows:
. Sometimes, it is more convenient to write the energy equation in entropy [36] [37] [38] or temperature [36] form as follows: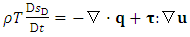 | (A.4) |
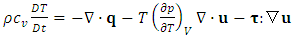 | (A.5) |
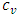 is the isochoric heat capacity. We reiterate that Eqs. (A.3), (A.4), and (A.5) are equal and have different forms simply for convenience.The definition of excess entropy is given by
is the isochoric heat capacity. We reiterate that Eqs. (A.3), (A.4), and (A.5) are equal and have different forms simply for convenience.The definition of excess entropy is given by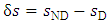 | (A.6) |
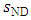 is the entropy mass density of a nondissipative fluid and
is the entropy mass density of a nondissipative fluid and 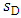 is the entropy mass density of a dissipative fluid. The idea is that when
is the entropy mass density of a dissipative fluid. The idea is that when 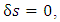 it is an isentropic motion; otherwise, it is dissipative. Introducing (A.6) into (A.4), we obtain
it is an isentropic motion; otherwise, it is dissipative. Introducing (A.6) into (A.4), we obtain 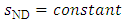
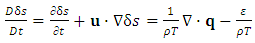 | (A.7) |
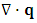 denotes the heat conduction and can be expressed as
denotes the heat conduction and can be expressed as 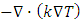 and
and 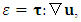 dissipation due to viscosity.From (A.7), if we can find an instant or a location,
dissipation due to viscosity.From (A.7), if we can find an instant or a location,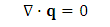 | (A.8) |
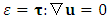 | (A.9) |
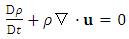 | (A.10) |
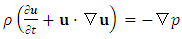 | (A.11) |
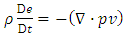 | (A.12) |
 | (A.13) |
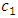 and
and 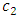 are the first and second sound for the momentum resonance and energy resonance, respectively. The integration of the governing equations of superfluid at resonance produces the following algebraic equations:
are the first and second sound for the momentum resonance and energy resonance, respectively. The integration of the governing equations of superfluid at resonance produces the following algebraic equations: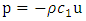 | (A.14) |
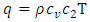 | (A.15) |
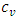 is the isochoric heat capacity and q is the heat flux. (A.14) is the super momentum flux, and (A.15) is the super energy flux.
is the isochoric heat capacity and q is the heat flux. (A.14) is the super momentum flux, and (A.15) is the super energy flux. 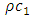 is the characteristic impedance of the first sound, a well-known quantity for acoustics of a given medium, and the negative sign in (A.14) says that pressure is out of phase with velocity.
is the characteristic impedance of the first sound, a well-known quantity for acoustics of a given medium, and the negative sign in (A.14) says that pressure is out of phase with velocity. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML