1. Introduction

Corrosion has been the subject of scientific study for more than 150 years. It is a naturally occurring phenomenon commonly defined as the deterioration of a material (usually a metal) or its properties because of a reaction with its environment. Like other natural hazards such as earthquakes or severe weather disturbances, corrosion can cause dangerous and expensive damage to everything from pipelines, bridges, and wastewater systems, and even home appliances. Unlike weather-related disasters, however, there are time-proven methods to prevent and control corrosion that can reduce or eliminate its impact on public safety, the economy, and the environment. The science of corrosion prevention and control is highly complex, exacerbated by the fact that corrosion takes many different forms and is affected by numerous outside factors. corrosion professionals must understand the effects of environmental conditions such as soil resistivity, humidity, and exposure to salt water on various types of materials; the type of product to be processed, handled, or transported; required lifetime of the structure or component; proximity to corrosion-causing phenomena such as stray current from real systems, appropriate mitigation methods, and other considerations before determining the specific corrosion problem and specifying an effective solution [1].

1.1. PM3 (Parameterized Model Number 3) Method

PM3 is another semi-empirical method based on the neglect of differential diatomic overlap integral approximation. The PM3 method uses the same formalism and equations as the Austin Model 1, AM1 method. The only differences are: (a) PM3 uses two Gaussian functions for the core repulsion function, instead of the variable number used by AM1 (which uses between one and four Gaussians per element); (b) the numerical values of the parameters are different. The other differences lie in the philosophy and the methodology used during the parameterization: whereas AM1 takes some of the parameter values from spectroscopic measurements, PM3 treats them as optimized values. The method was developed by Stewart and first reported in 1989 [2].

1.2. Ab Initio and Density Functional Theory (DFT) Methods

Quantum mechanical methods (ab initio, density functional theory (DFT) and semi empirical PM3) are all based on solving the time independent Schrodinger equation for the electrons of a molecular system as a function of the positions of the nuclei. The term ab initio indicates that the calculation is from first principles and that no empirical data is used.

The simplest type of ab initio electronic structure calculation is the Hartree Fock (HF), in which the instantaneous Columbic electron–electron repulsion is not specifically taken into account and only its average effect is included in the calculation. This is a variational procedure, and therefore, the obtained approximate energies, expressed in terms of the system wave function, are always equal to or greater than the exact energy, and approach a limiting value called the Hartree–Fock limit as the size of the basis is increased [3]. Many types of calculations (Moller-Plesset perturbation theory) begin with a Hartree–Fock calculation and subsequently correct for electron–electron repulsion, referred to also as electronic correlation.

Density functional theory (DFT) is used to investigate the electronic structure, principally the ground state of many-body systems, in particular atoms, molecules and the condensed phases. The main objective of DFT is to replace the many-body electronic wave function with the electronic density as the basic quantity [4]. Any exchange functional can be combined with any correlation functional in DFT calculations. For example, the notation BLYP/ 6-31G* denotes a density functional calculation done with the Becke 1988 exchange functional and the Lee-Yang-Parr correlation functional, with the orbitals expanded in a 6-31G* basis set [5].

Density Functional Theory (DFT) [6,7] which is an economic and efficient quantum chemistry computing method can provide accurate information about geometrical configuration and electron distribution. DFT is widely applied in the analysis of corrosion inhibition performance and the interaction of corrosion inhibitors and interfaces [8-9]. The B3LYP functional was applied within the context of Gaussian 09 [10], using the 6-31+G (d, p) basis set [11,12]. Optimized structures were verified as minima via the presence of all positive harmonic frequencies. In the aqueous phase calculations, the theoretical model was considered via SMD, using a dielectric constant of 78.5 for water [13a,13b]. Frequency analysis showed there was no imaginary frequency, indicating that the calculated geometry represented a stable minimum on the potential energy surface.

The aim of this work is to perform a theoretical calculations on thiophene oligomers (1 to 10) by using DFT and PM3 methods to calculate the quantum chemical parameters such as the chemical hardness (η), the chemical softness (σ), the absolute electronegativity (χ), the electrophilicity index (ω), and the fractions of electrons transferred (ΔN). Also to calculate E_HOMO, E_LUMO, ΔE = (E_LUMO-E_HOMO) to find a correlation between these parameters and the efficiency of thiophene oligomers (1 to 10) as corrosion inhibitors for iron metal.

2. Results and Discussion

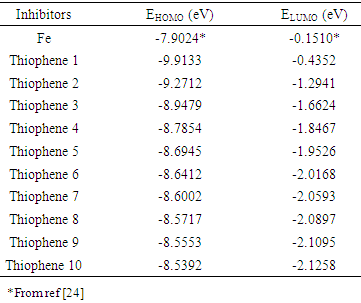
The thiophene Oligomers under investigation and its structures are shown in Scheme. 1, and the energy of the frontier molecular orbitals, (E_HOMO and E_LUMO), the energy gap (ΔE), the chemical softness (σ), the chemical hardness (η), and the fraction of the electron transferred (ΔN), and elecrophilicity index (ω), were calculated according to molecular orbital theory [14]. The E_HOMO and E_LUMO of the inhibitor are related to ionization potential (I) and electron affinity (A) respectively, with reversed sign.

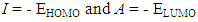
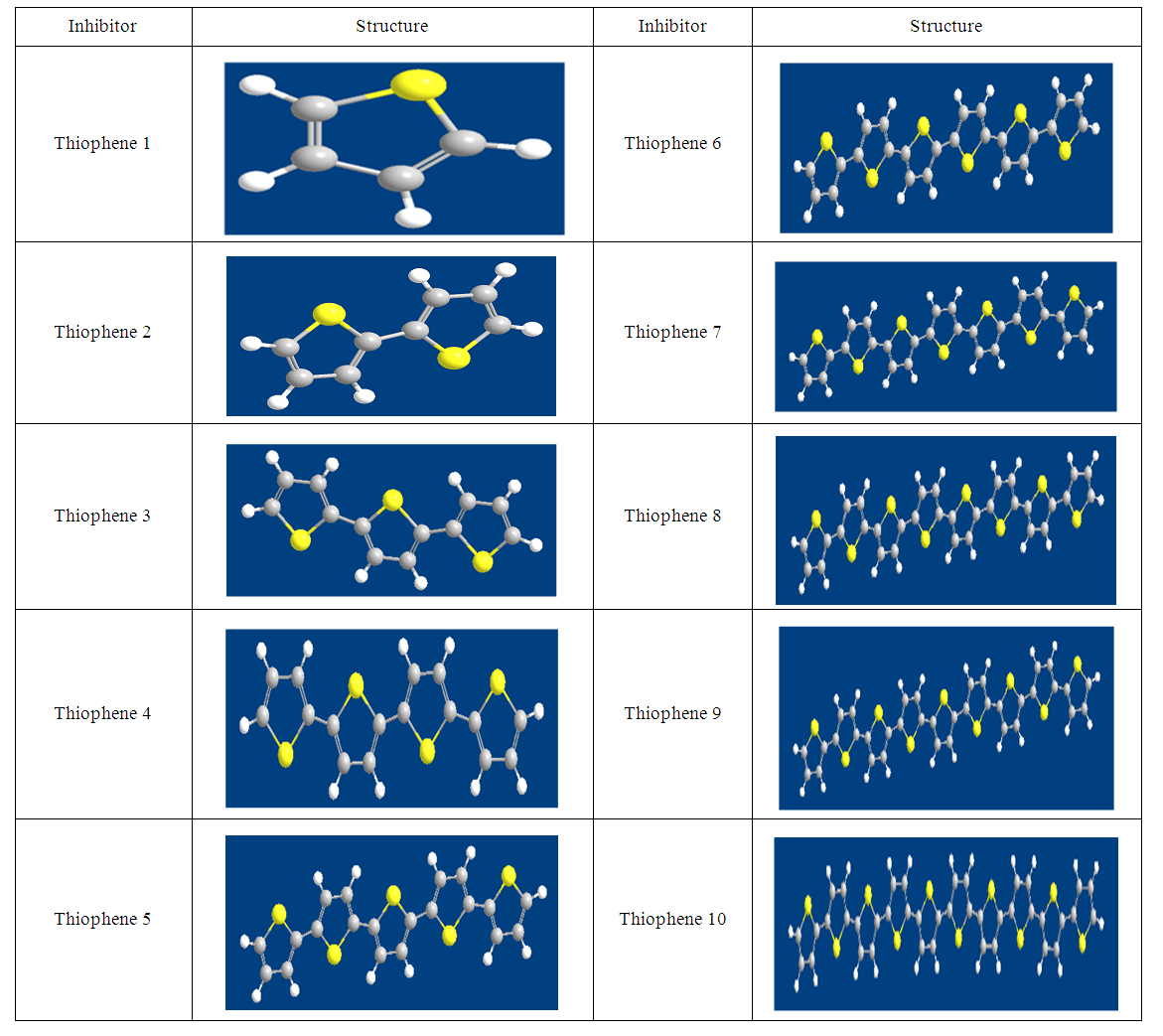Scheme 1. Optimized molecular structures of thiophene oligomers are given in figures (1-10)

The higher the HOMO energy the more reactive molecule in the reactions with electrophiles, whereas lower LUMO energy is essential for molecular reactions with nucleophiles [15]. Electronegativity χ and chemical hardness η of the inhibitor are calculated according to the following formula:

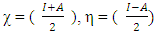The global softness (σ) is the inverse of the chemical hardness [16].

Electronegativity, hardness and softness have been proved to be very useful quantities in the chemical reactivity theory. When two systems, metal and inhibitor, are brought in contact together, electrons will flow from lower (χ) inhibitor to higher (χ) metal, until the chemical potentials become an equal. The fraction of the transferred electronic charge (ΔN) from the inhibitor molecule to the metallic atom was calculated according to Pearson formula [17]. For a reaction of two systems with different electronegativities (as a metallic surface and an inhibitor molecule). The following mechanism will take place: the electrons will flow from the molecule of lower electronegativity value toward that of higher value, until the chemical potentials are the same.

The global electrophilicity index was introduced by Parr et al.: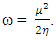

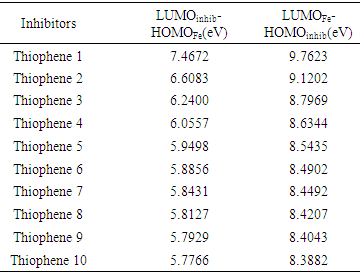
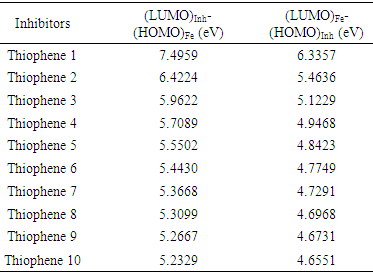
Where μ represent the chemical potential and equal to the negative value of electronegativity χ [20]. According to the definition, this index measures the propensity of chemical species to accept electrons.

The following formula was used to calculate ΔN. [18]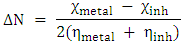

Where χ_metal and χ_inh denote the absolute electronegativity of metal and inhibitor molecule respectively, η_metal and η_inh denote the absolute hardness of metal and the inhibitor molecule respectively. The difference in electronegativity drives the electron transfer, and the sum of the hardness parameters acts as a resistance [1].

2.1. PM3 Calculations

Table 1. Calculated (HOMO – LUMO) energies in eV. of the thiophene oligomers PM3 method

The energy of the highest occupied molecular orbital (E_HOMO) measures the tendency towards the donation of electron by a molecule [21]. High values of E_HOMO have a tendency of the molecule to donate electrons to appropriate acceptor molecules with low energy, empty molecular orbital. Therefore, higher values of E_HOMO indicate better tendency towards the donation of electron. E_LUMO indicates the ability of the molecule to accept electrons. The binding ability of the inhibitor to the metal surface increases with increasing of the HOMO and decreasing of the LUMO energy values. According to the frontier molecular orbital theory (FMO) of chemical reactivity, transition of electron is due to interaction between highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) of reacting species [22]. E_HOMO is a quantum chemical parameter which is often associated with the electron donating ability of the molecule. High value of E_HOMO is likely to a tendency of the molecule to donate electrons to appropriate acceptor molecule of low empty molecular orbital energy [23]. The energies of highest occupied molecular orbitals (HOMO) and lowest unoccupied molecular orbitals (LUMO) values of iron (Fe) were compared to the values calculated for thiophene oligomers to determine the type of the interaction.

Table 2. HOMO-LUMO gap energy interactions of iron with thiophene oligomer

According these calculations iron will act as a Lewis base while the inhibitors thiophene oligomers act as Lewis acids. Thus thiophene oligomers act as cathodic inhibitors. So iron will utilize the HOMO orbital to initiate the reaction with LUMO orbital of the thiophene oligomers. The interaction will have certain amount of ionic character because the values of LUMO_inh- HOMO_Fe gap fall between 5 and 7 eV. Strong covalent bond can be expected only if LUMO_inh- HOMO_Fe gap is approximately zero eV [25]. The separation energy (ΔE), the electronegativity (χ), global chemical hardness (η), global softness (σ), the fraction of electrons transferred (ΔN) and elecrophilicity (ω) are involved in Table 3.

The energy gap (Table 3), (ΔE = E_LUMO – E_HOMO) is an important parameter, as a function of reactivity of the thiophene oligomer molecules towards the adsorption on the iron metallic surface. As ΔE decreases the reactivity of the molecule increases, lower values of the energy difference will render good inhibition efficiency [26]. Ionization energy (I) is a fundamental descriptor of the chemical reactivity of atoms and molecules. High ionization energy indicates high stability and chemical inertness and low ionization energy indicates high reactivity of the atoms and molecules [27]. The low ionization energy indicates the high inhibition efficiency. Absolute hardness and softness are important properties to measure the molecular stability and reactivity. It is apparent that the chemical hardness fundamentally signifies the resistance towards the deformation or polarization of the electron cloud of the atoms, ions or molecules under small perturbation of chemical reaction. A hard molecule has a large energy gap and a soft molecule has a small energy gap [28]. Normally, the inhibitor with the least value of global hardness (hence the highest value of global softness) is expected to have the highest inhibition efficiency [29]. The global electrophilicity index measures the propensity of chemical species to accept electrons. A good, and reactive, nucleophile is characterized by lower value of (ω) and conversely a good electrophile is characterized by a high value of (ω). This new reactivity index measures the stabilization in energy when the system acquires an additional electronic charge ΔN from the environment [30].

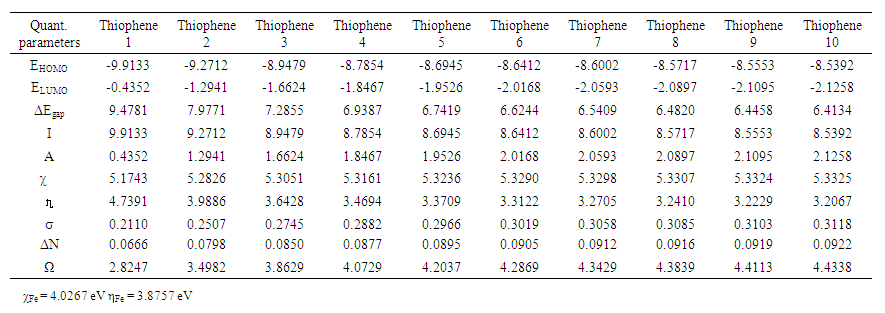Table 3. Calculated quantum chemical parameters for the Thiophene oligomers inhibitors for iron

From Table 3, it can be seen that the energy gap (ΔE), ionization energy (I) and hardness (η) for inhibitors thiophene oligomers decreases with increasing in the number of thiophene molecules while the electron affinity (A), softness (σ), electronegativity (χ), electrophilicity (ω) and (ΔN) increases with increasing in the number of thiophene molecules (cathodic inhibitors). So, the efficiency of thiophene oligomers as inhibitors increases with increasing in the number of thiophene units in thiophene molecules.

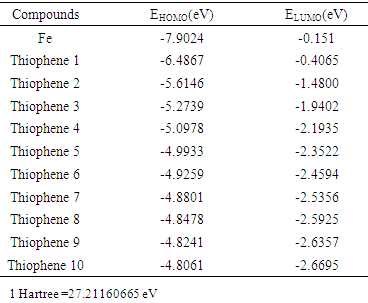
2.2. Density Functional Theory (DFT) Calculations

Calculated (HOMO –LUMO) energies of the thiophene oligomer inhibitors by DFT method shown in. Table 4.

Table 4. Calculated (HOMO –LUMO) energies of the thiophene oligomer by DFT method

From HOMO-LUMO energy gap of iron and thiophene oligomers, Table 5, it can be seen that iron (Fe) will act as a Lewis base while the thiophene oligomer act as a Lewis acids. Thus iron will utilize the HOMO orbital to initiate the interaction with LUMO orbital of the thiophene oligomers. The interaction will have certain amount of ionic character, because the energy difference between highest occupied and lowest occupied orbitals (LUMO_inh - HOMO_Fe (energy gap) falls between 6 and 4 eV. A strong covalent bond can be expected only if LUMO_inh - HOMO_Fe gap is approximately zero eV. [31]. From the calculated (HOMO –LUMO) energies of the thiophene oligomers by DFT method (Table 6) It can be concluded that iron acts as a Lewis acids while thiophene oligomers act as a Lewis base (Table 6). In this case, thiophene oligomers act as anodic inhibitor. The separation between the highest and lowest occupied energies, ∆E_gap = (E_LUMO – E_HOMO), is an important parameter, as shown in Table 6, and it is a function of tendency of inhibitor molecules towards the adsorption on metallic surface (Iron surface). As ∆E_gap decreases, the reactivity of the molecule increases, This leading to an increase in the inhibitors efficiencies [32].

Table 5. HOMO-LUMO gap energy of iron and thiophene oligomers

The effectiveness of thiophene oligomers as inhibitors has been further addressed by evaluating the global reactivity parameters such as electronegativity, χ, global chemical hardness, η, global softness, σ, fraction of transferred electrons, ∆Ν, from the inhibitor to an iron, and the electrophilicity, ω, are tabulated in Table 6. According to these calculations, iron will act as a Lewis acid while the inhibitors thiophene oligomers act as a Lewis base. Thus the thiophene oligomers inhibitors act as anodic inhibitors, these results differs from PM3 calculations where thiophene oligomers inhibitors act as cathodic inhibitor). From calculated quantum chemical parameters for the thiophene oligomers inhibitors (Table 6) it can be seen that the donation of electron (ΔN) by the inhibitors to the iron (anodic inhibitors) decreases with an increasing in the number of thiophene units in the thiophene oligomers.

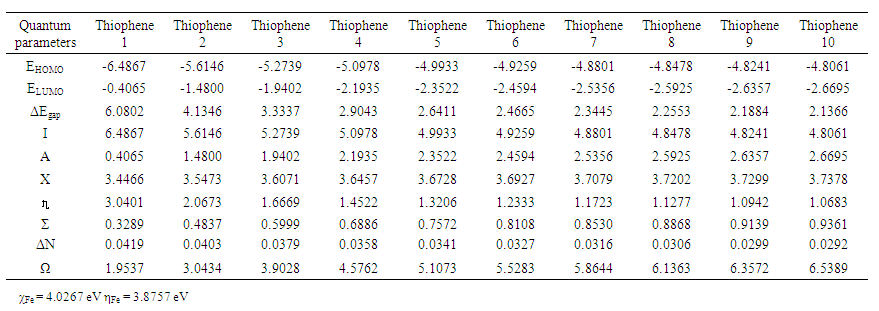Table 6. Calculated quantum chemical parameters for (1- 10) thiophene oligomers

The bonding tendencies of the inhibitors towards the metal atom can be discussed in terms of HSAB (Hard –Soft – Acid – Base ) and the frontier orbitals -controlled interaction concepts [33a,33b,34]. General rule suggested by the principle of HSAB, is that hard acids prefer to co-ordinate to hard bases and soft acids prefer to co-ordinate to soft bases. On the other hand, metal atoms are known as soft acids [35]. Hard molecules have a high HOMO-LUMO gap and soft molecules have a small HOMO-LUMO gap [36]. And thus soft bases inhibitors are the most effective for metals [37]. So thiophene oligomers which have the lowest energy gap and the highest softness have the best efficiency, This could also be confirmed by calculating another quantum chemical softness (σ). This parameter measures softness of the molecules and its reactivity. Table 6, shows the fraction electrons transferred (∆Ν). The values of (∆Ν) show the inhibitor efficiency resulting from an electron donation by the inhibitor to the iron metal [38]. The inhibitor efficiency increases by increasing the ability of the oligomers to donate electrons to the iron metal. The larger fraction of electrons transferred to the iron the better the inhibitor.

The electrophilicity index, (ω), shows the ability of the inhibitor molecules to accept electrons. The values of increases as the number of pyrrole molecules increases, suggesting that an increase in the ability of the thiophene oligomers to accept electrons from iron will be increased [39].

3. Conclusions

The present theoretical study indicates the following facts or observations:

- It was found that the interactions of the thiophene oligomers with iron have certain ionic character by both PM3 and DFT methods, because the values of LUMO_inh- HOMO_Fe gap fall between 5 to7 eV, by PM3 calculations, and between 4 to 6 eV, DFT calculations. Strong covalent bond can be expected only if LUMO_inh- HOMO_Fe gap is approximately zero eV.

- DFT and PM3 calculations have shown a better interaction by increasing the number of the thiophene unit in the oligomers.

- Thiophene Oligomer will therefore be a good and effective inhibitor. This agrees with the recently published experimental results [40].

Also, this study, displays a good correlation between corrosion inhibitor efficiency and number of thiophene unit and confirms the reliability of the theoretical methods to study the corrosion inhibitors for metal surfaces.