1. Introduction

The skeletal shapes of boranes, transition metal carbonyl clusters and their relatives have fascinated many scientists and continue to do so [1-10]. A keen interest to find if there was a simple pattern within metal carbonyl clusters was developed by first analyzing the osmium carbonyl clusters [11-13]. A relationship expressing the valence electron content of a fragment given by V=S= 14n+q (V = number of valence electrons, S = series, n= number of skeletal elements in a fragment, q = is a variable number) was formulated [11-13]. This relationship was found to be applicable to rhodium, rhenium and palladium carbonyl clusters as well as the Zintl and golden clusters [14-16]. A similar parallel relationship S= V = 4n+q for main group cluster elements was also identified [14, 15]. An isolobal relationship between the series formula for transition metal clusters and those of the main group elements was discerned [16, 17]. This is expressed by a simple equation:

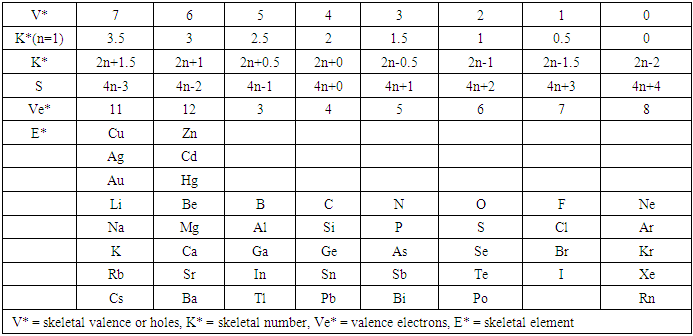
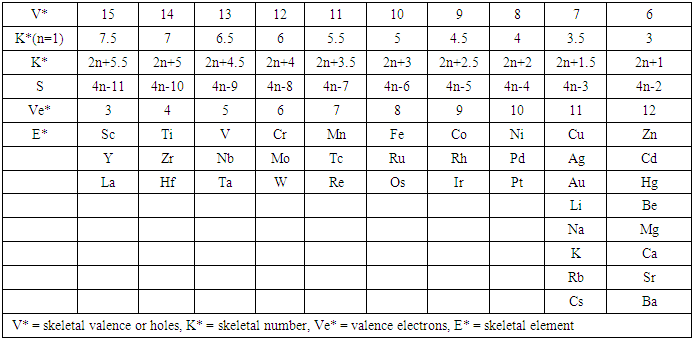
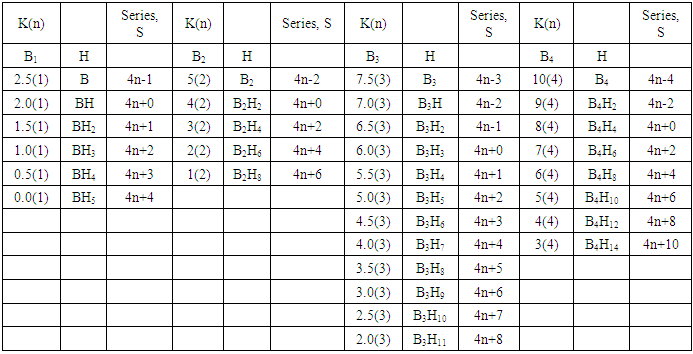
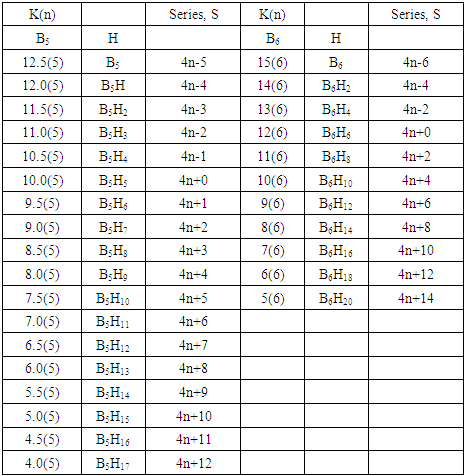
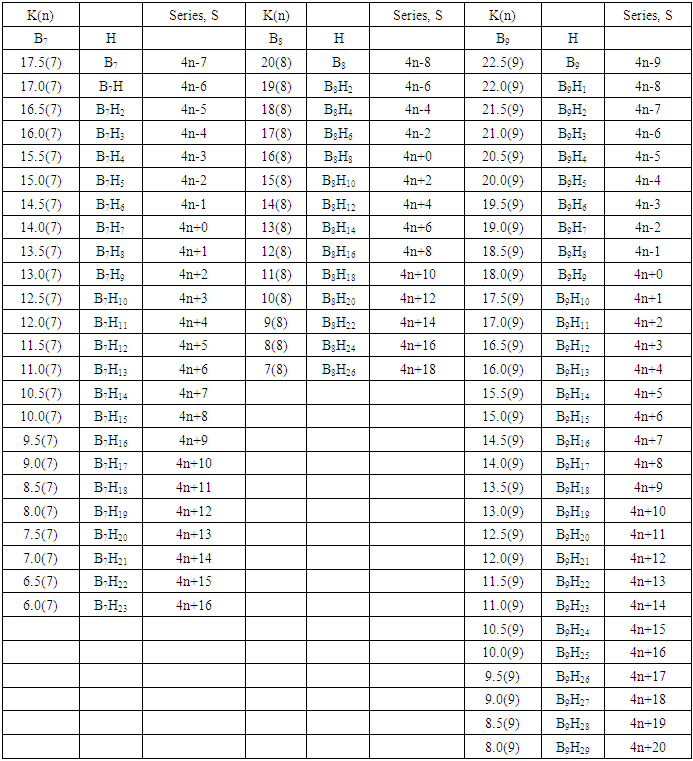
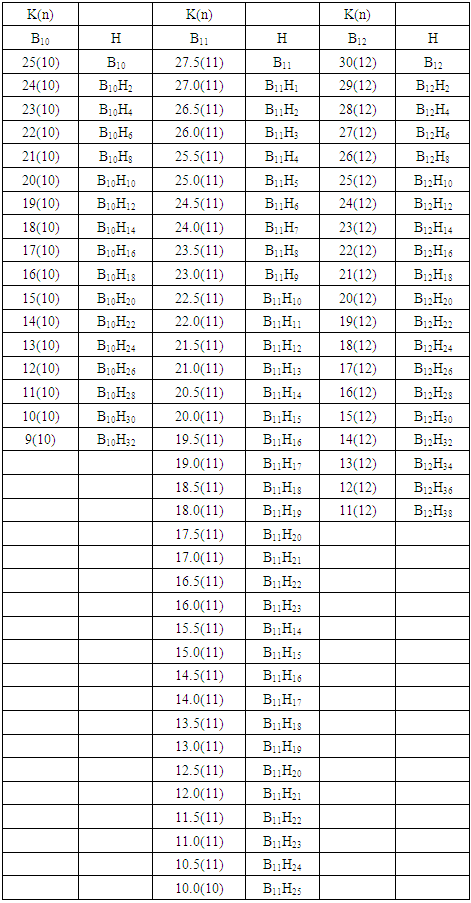
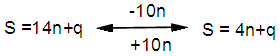q =0,-2,-4,-6,-8, etc for capping clusters, and q = 2,4,6,8, etc for un-capping clusters.

Due to isolobal relationship above, it was proposed to use the series term S =4n+q for all clusters except when determining the number of valence electrons of a fragment or cluster in which case adjustment is done accordingly [18]. Further development took place when the series method was utilized to derive skeletal numbers for elements and ligands [19]. The skeletal numbers have been exceedingly useful tools for categorizing clusters and providing some tentative prediction of the skeletal cluster shapes [15, 16].

The Numerical Power of Skeletal Numbers

The skeletal numbers are extremely useful in electron counting of valence electrons in fragments and clusters. Some of the outstanding applications of skeletal numbers have already been stated [20]. The skeletal numbers can be considered as a simple guide for analyzing clusters and fragments. In the 4n series method (hereafter referred to as the series method), the valence electrons of skeletal elements of the main group and transition metals and ligands are transformed into numbers which are utilized to categorize clusters and even provide, in some cases, tentative structural prediction. In other words, the series method empirically derived by close analysis of cluster sequences can be regarded as a simple ‘telescope’ for examining chemical clusters. The numbers are simple and very precise in their analysis of clusters. For example, clusters with [K (n) = 6(4), meaning 6 linkages to 4 skeletal elements] tend to adopt a tetrahedral shape, whereas K(n) = 9(5) adopt a trigonal bipyramid one and 11(6) an octahedral shape [18]. Therefore, we must add sensible chemical interpretation to what is observed. Recently the meaning of skeletal number was introduced as well as its interpretation [21]. For the purpose of this article, the skeletal number was interpreted as the number of the electron pairs required by an element to attain the 8-electron or 18-electron configuration for main group or transition metal elements respectively [21]. The value of electrons corresponding to the skeletal number of an element can be regarded as a SKELETAL VALENCE of that element. Using the skeletal number and valence elements, the analysis of structures of molecules and clusters and their formulas is greatly simplified. This will be illustrated by numerous examples to be covered in this paper.

GENESIS OF 14n/4n SERIES AND K VALUE

The origin of 14n series for carbonyl clusters was discovered when it was found that a SINGLE FRAGMENT OF OSMIUM, [OS(CO)₃] could be utilized as a fulcrum to generate all the osmium clusters and fragments both known and unknown [12] The fragment [Os(CO)₃] has a valence electron content of 14 (8+3x2). This fragment was assigned the series symbol of S = V = 14n+0 where S = series, V = valence content and when n=1, V= 14(1) +0 = 14. The addition of a CO ligand, 2 electrons are added to [Os(CO)₃], and it becomes [Os(CO)₄], then S = V = 14n+2(where n=1). With further addition of a CO ligand to [Os(CO)₄], we get [Os(CO)₅], S = V = 14n+4(n=1)= 14+4 = 18. Thus Os(CO)₅ fragment obeys the 18 electron rule. However, if we remove a CO ligand from [Os(CO)₃], we get [Os(CO)₂] and the corresponding series formula becomes S= V= 14n-2[n=1, S=V=14(1)-2= 12]. The value of S=V = 12 is the electron valence content of the fragment, [Os(CO)₂]. The removal of CO ligands can continue until all of them have been removed, then we get the ‘naked’ [Os] skeletal element. The corresponding fragments generated with their series are as follows: Os[S= V=14n-6=14-6=8]; Os(CO)[S=V= 14n-4 = 14-4=10], Os(CO)₂[S=V=14n-2=14-2 = 12], Os(CO)₃[S=V=14n+0 = 14],Os(CO)₄[S=V=14n+2 = 14+2 = 16] and Os(CO)₅[S=V=14n+4 = 14+4 = 18]. This list represents all the possible fragments we can generate from nuclearity one {N1) for osmium carbonyl clusters. This process is shown in Scheme S-3. In the same manner, the cluster fragments of Nuclearity two(N-2) from Os₂(CO)₆[S=V=14n+0, n=2], Nuclearity three(N-3) Os₃(CO)₉[S=V=14n+0, n=3], Nuclearity four(N-4) Os₄(CO)₁₂[S=V=14n+0, n=4], and so on may be derived. The details of this work has already been published [12]. It was also found that K is related to the number of skeletal elements in a fragment or cluster(n) by K =2n- ½ q where q is from the series S =14n+q (transition metals) or 4n+q (main group elements) [12]. The possible transition metal fragments that can be utilized to generate hypothetical carbonyl cluster formulas are shown in Tables 2 and 3. The fragments of the 14n+0 series of nuclearity index 2-20 can be regarded as the backbone from which other corresponding fragments can be generated. A selected sample of some of these are included in Tables 2 and 3 for illustration purposes. The formation of 14n+0 of some clusters from just one central fragment are simply illustrated numerically in Scheme 2 and demonstrated by N-1 for osmium. This is shown in scheme 3. The numbers, 1→Os(CO)₃, 2→Os₂(CO)₆, 3→Os₃(CO)₉, and so on. The selected derived skeletal fragments and clusters are given in Tables 2 and 3. Just as the osmium carbonyl formulas can be derived from a single mono-skeletal fragment [Os(CO)₃], S = 14n+0; the borane formulas can readily be derived from the mono-skeletal fragment [BH], S =4n+0. Surprisingly, the results so obtained shown in Table 4 reproduces those obtained in earlier work [23].

The series(14n/4n) method has developed to a level where elements of transition metals and main group elements and the ligands have been assigned skeletal numbers [21]. This implies that we can categorize and analyze cluster formulas numerically in a simpler and faster manner, regardless of the size. This has been demonstrated in previous work [18]*. The formulas of clusters can be generated using the fragments from S = 14n+0 as foundations. For example, the following clusters can easily be derived using the appropriate fragments which are members of S =14n+0 family, F₁= [Os(CO)₃](S =14n+0)+2CO→Os(CO)₅(S=14n+4); F₂ = [Os₂(CO)₆](S=14n+0)+3CO→Os₂(CO)₉(S=14n+6); and F₃ = [Os₃(CO)₉](S =14n+0])+3CO→Os₃(CO)₁₂(S =14n+6);F₄= [Os₄(CO)₁₂](S=14n+0)+2CO→Os₄(CO)₁₄(S=14n+4); F₅ =[Os₅(CO)₁₅](S =14n+0)+1CO→Os₅(CO)₁₆ (S =14n+2) and F₆=[Os₆(CO)₁₈](S=14n+0).

SKELETAL LINKAGES WITHIN A CLUSTER

We know that the simple hydrocarbon molecules G₁= C₂H₂[S=4n+2], G₂= C₂H₄[S=4n+4] and G₃= C₂H₆[S =4n+6] possess triple, double and single bonds respectively. After a very careful analysis of a wide range of clusters from main group and transition metals, it was found that the linkages of skeletal elements are given by K = 2n- ½ q where n is the number of skeletal elements in a cluster and q is a variable from the corresponding cluster series. Thus, for G₁, K₁ = 2n-1 = 2(2)-1 = 3; G₂, K₂ = 2n-2=2(2)-2=2; and G₃, K₃ =2n-3=2(2)-3=1. Similar calculations have been done in previous work [15-20] but it is repeated here for emphasis as the series method approach to cluster categorization is new. The development of the series method from the use of 14n/4n fragments to using skeletal valences is summarized in Scheme S-1. The skeletal number of a cluster, K(n) originates from the parental naked (without ligands) clusters. Since some of these values are going to be utilized in the examples to follow, the skeletal numbers have been reproduced in Tables 5 and 6. These tables also indicate the derivation of the skeletal K values from the respective series as well as the skeletal valences of the elements. Although the cluster fragments and clusters can be generated readily using the 14n/4n fragments, they can similarly be generated using the series (S = 4n+q) as well as skeletal numbers. This procedure is being extended to boranes and examples are shown in Tables 7-10.

S-1 The evolution of skeletal numbers and valences

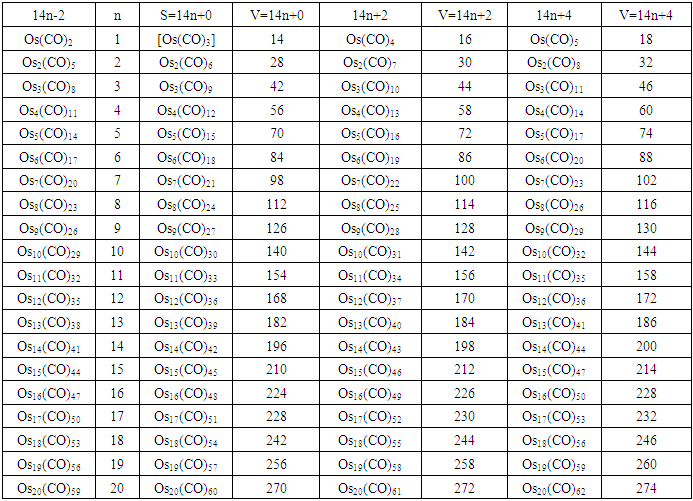
S-2 Multiples of Principal Fragment [Os(CO)3]

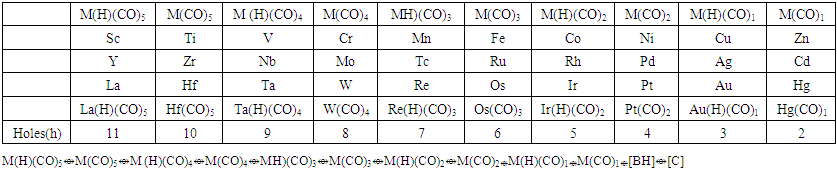Table 1. The 14 electron principal fragments for deriving transition metal carbonyl clusters

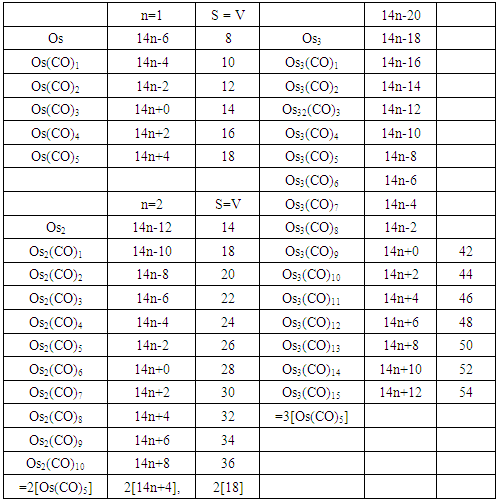
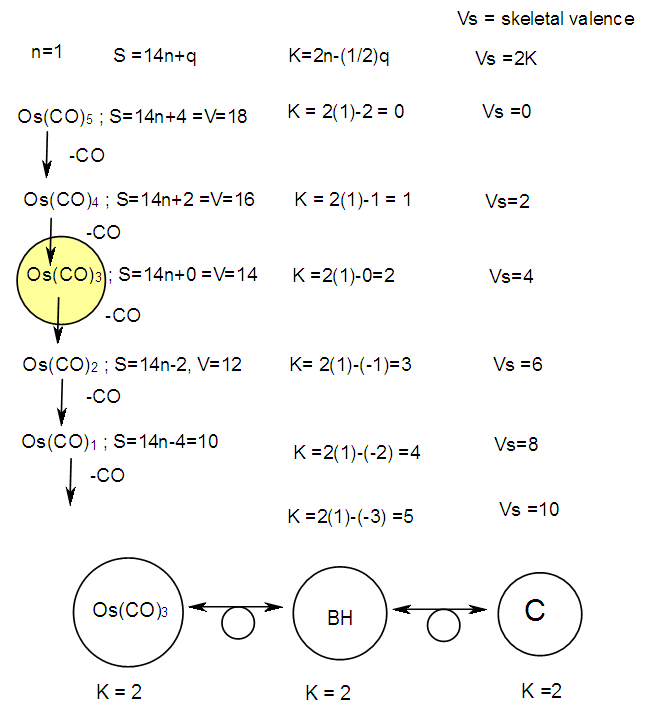S-3 Derived carbonyl fragments of osmium of nuclearity 1

Table 2. Selected derived carbonyl fragments

Table 3. Derivation of carbonyl fragments for osmium of nuclearity 1 and 2

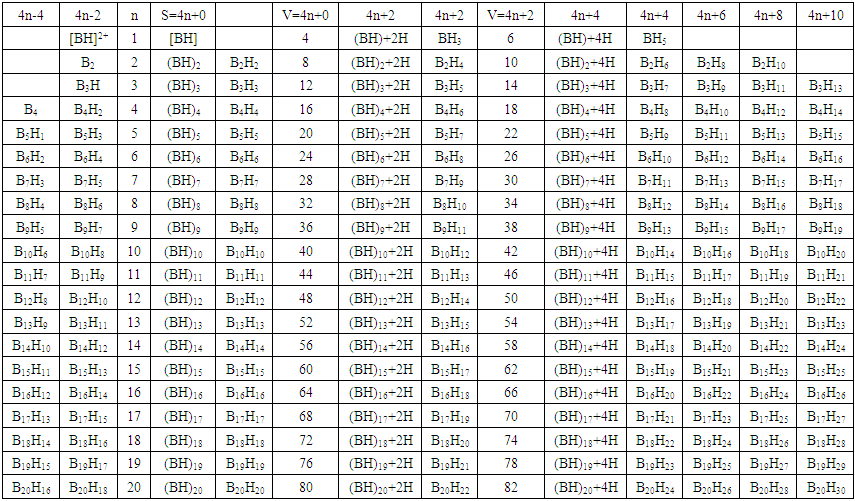Table 4. Borane formulas derived from the principal fragment [BH]

Table 5. The skeletal numbers and valences of main group elements

Table 6. Skeletal numbers and valences of transition metals

2. Results and Discussion

BORANE NUCLEARITY TREES

B₁ NUCLEARITY TREE

As pointed out earlier, nuclearity trees of chemical clusters can be generated in three ways so far. First, they can be derived using a [V=14] electron fragment in case of transition metals or [V=4] electron fragment for main group elements. Secondly, they can be derived using the series formula(S=4n+q), and thirdly they can be obtained using skeletal numbers [K(n), starting with naked clusters. In this paper, the emphasis will be focused on the derivation of cluster formulas of boranes using skeletal numbers. In the case of the boron skeletal element, the K value derived from series method is 2.5 and its corresponding skeletal valence is 5, and may be viewed as HOLES on the skeletal element waiting to be filled by electrons from donors (ligands). The addition of a hydrogen ligand atom [H] to the skeletal boron element [B] results in the decrease of its K value by 0.5 according to the series method [20]. Successive addition of [H] ligands to the boron atom is shown in Scheme 4 and also diagrammatically expressed in Figure 1a for group three elements and Figure 1b for the boron atom. The 5 holes on the boron skeletal atom can be defined as its skeletal valence which it exerts in its quest to attain the 8 electron configuration during the formation of borane clusters. In case of a transition metal such as rhenium with K = 5.5 and V = 11, we can add H ligands stepwise on it until all the 11 holes(h) have been filled so as to produce the hypothetical complex ReH₁₁(K =0) which obeys the 18 electron rule. This is shown in Scheme 5. It is interesting to know that the complex ions such as ReH₆^5―(h = 11), ReH₉^2―(h = 11), FeH₆^4―(h =10), RhH₅^4―(h = 9), PtH₄^4―(h = 8), NiH₄^4―(h = 8), CuH₄^3―(h = 7) and ZnH₄^2―(h = 6) are known[22]. It must be emphasized that according to series approach, both [H] ligand and [―] are regarded as equal ligands.

Scheme 4. Stepwise addition of H ligands on boron skeletal element

This constitutes the borane fragments of boron of nuclearity B₁. The above Scheme 4 demonstrates the derivation of borane fragments of B₁ nuclearity using skeletal numbers. The fragments form series. For instance, [B], K(n) = 2.5(1): S = 4n-1; [BH], K(n) = 2(1), S = 4n+0, [BH₂], K(n) = 1.5(1), S = 4n+1; [BH₃], K(n) = 1(1), S = 4n+2; [BH₄], K(n) = 0.5(1), S = 4n+3; [BH₅], K(n) = 0(1), S = 4n+4. The concept of nuclearity tree in which (∆n = 0) was recently introduced [21].

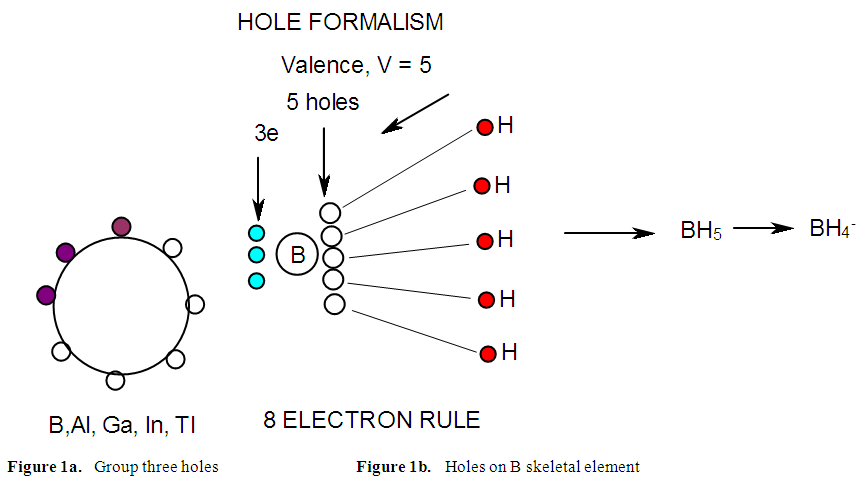Figure 1a and 1b

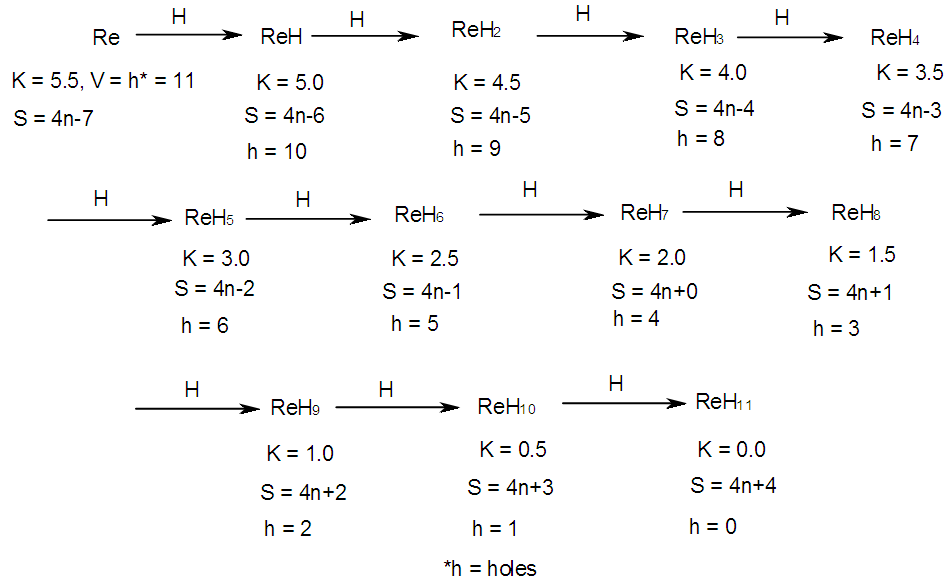Scheme 5. Stepwise addition of H ligands onto rhenium skeletal element

B₂-B₁₂ NUCLEARITY TREES IN TABULAR FORM

In the case of nuclearity two [B₂ series], the initial K = 2x2.5 = 5. This information is expressed as K(n) = 5(2). The addition of 2H ligands to B₂ will generate the fragment [BH₂] and reduce the K value by 1(K = 4). This information is expressed as K(n) = 4(2). The derived formulas of B₂ nuclearity fragments are given in Table 7 while the hypothetical structures of borane fragments associated with B₂ nuclearity are given in Scheme 6. The K values decrease from 5→4→3→2→1.

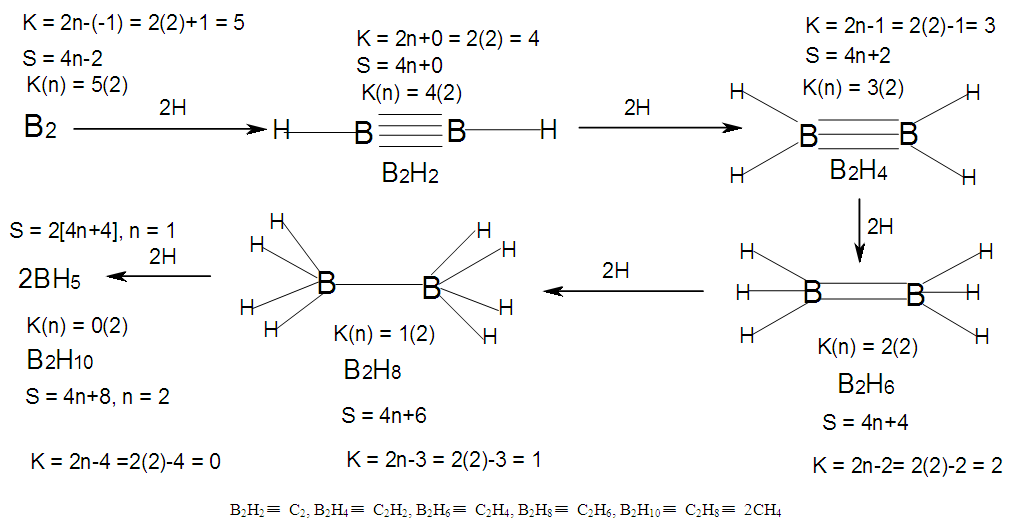Scheme 6. Hypothetical shapes of clusters generated from B2 nuclearity tree

The B₂H₄ borane may be considered to be represented by B₂L₂ cluster [6] shown in Figure 2.

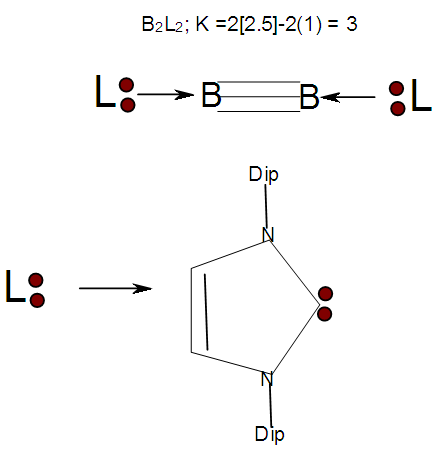Figure 2. Ligand known to stabilize boron-boron triple bond

As can be seen from Scheme 6, at every step, the [B] element maintains a skeletal valence of 5. According to the 4n series method, the reasonable fragments for nuclearity clusters are related by n and K values as follows: n = 1, last K-value is 0; n =2, last K = 1; n=3, last K = 2; n = 4, last K = 3; n = 5, last K =4; n = 6, last K = 5; n = 7, last K = 6, and so on. This means that in case of boranes, the B₁ fragments will start with K = 2.5 and end with K = 0, B₂ fragments will start with K = 2x2.5 = 5 and end with K = 1, B₃ will start at K = 3x2.5 =7.5 and end at K = 2, B₄ will start with K = 4x2.5 = 10 and end at K = 3 and so on. This gives us the fragments generated from nuclearity two to twelve [B₂-B₁₂] of boron elements which are shown in Tables 7-10. The derivation of borane trees without using skeletal numbers was earlier discerned [23]. At that time, also the interpretation of the K value and its proper linkage to different clusters such as carboranes and metalloboranes and fragments had not yet been discovered [23]. Many of the common boranes known for B₂-B₁₂ such as B₂H₆, B₄H₁₀, B₅H₁₁, B₅H₇ (B₅H₅^2―)^, B₈H₁₄, and B₁₂H₁₂^2―(B₁₂H₁₄) can be identified in the Nuclearity Trees represented in Tables 7-10. The K values of the clusters originate from the parental naked skeletal clusters. The K values shown in Tables 7-10 can directly be calculated from the corresponding borane formulas in accordance with the principle that the skeletal elements provide intrinsic skeletal linkages some of which are utilized by ligands and those left over form the BASIS FOR CLUSTER NUMBER LINKAGES, K(n) PARAMETER. The K(n) parameter has a double meaning; it represents the number of skeletal linkages within the cluster as well as the number of electron pairs required by the cluster to enable all the skeletal elements to satisfy the octet (8) for main group or eighteen (18) electron rule for transition metals [20]. For instance, for B1(K = 2.5), this means that 1 boron skeletal element needs 2.5 electron pairs provided by ligands either as H atoms or negative charges or a mixture of the two in order to obey the 8 electron rule. Thus, B + 5e→B^5―; B+ 5H → BH₅; B +4H +e → BH₄^―. In this case, all the species B^5―, BH₅, BH₄^― obey the 8 electron rule. Similarly, rhenium with K = 5.5 has a valence of 11. This means it can attain the 18 electron configuration by receiving 11 electrons from donating ligands.

Table 7. Boranes derived using skeletal numbers

Table 8. Derived boranes for nuclearities B5 and B6

Table 9. Derived boranes of nuclearities B7 to B9

Table 10. Derived boranes of nuclearity B10 to B12

3. The Skeletal Valence of Five in Borane Clusters, Raw Skeletal Structures, and Structural Rearrangements

In the case of the mono-skeletal boron element, the hypothetical fragment BH₅ may be considered to be represented by known complexes such as H₃B(CO), H₃B(NR₃), and H₃B(PR₃). Let us take B₂H₆ as another example to illustrate the concept of skeletal valence 5 for the boron atom. The molecule B₂H₆ has a K value of 2 as can be read from Tables 5 and 6. This value can be derived by a simple calculation K = 2[2.5]-3 = 2. This is based on the concept of skeletal numbers introduced recently [19]. The K value of 2 for B₂H₆ means that the two skeletal boron atoms are linked by 2 skeletal bonds. If we link up the two boron atoms with 2 bonds and add on the 6 hydrogen atom ligands in such a way that the skeletal valence of 5 for [B] skeletal elements is obeyed then the formula of the molecule, in this case B₂H₆ is naturally derived. This is shown in Scheme 6 and F-3 - F-5. It is proposed that the skeletal structures shown in F-3 - F-5 before rearrangement be referred to as RAW SKELETAL STRUCTURES. The ‘raw B₂H₆’ structure assumes that all the 5 linkages have donated electrons to the [B] skeletal atom to enable the [B] skeletal element achieve the 8 electron rule which is not the case if we assume that its electrons are involved in the formation of B-H bonds. The 3H ligands have donated 3 electrons but the 2 bonds from the linked [B] skeletal atom have not. Hence, there is a need for the raw structure to undergo rearrangement in order for it to ‘normalize’ the skeletal bonds by donating two electrons (2e). We can then consider the achievement of this to occur by the transfer of a hydrogen ligand with two electrons (H:) and inserting itself in one of the empty B=B skeletal bonds. If two such coordinated hydrogen ligands (H:) ligands insert themselves in the ‘empty’ B=B bonds, we get what is referred to as the BANANA bonds. Such rearrangement creates bonds of a shape which obeys the 8 electron rule and becomes isoelectronic to C₂H₄(H₂C=CH₂), thus the rearranged structures F-3 to F-5 which obey the octet rule are obtained. The best way to observe the purpose of STRUCTURE REARRANGEMENTS is to compare similar isomeric structures of the corresponding hydrocarbons. Thus a B₂H₆ can be treated as (BH)₂H₄ = C₂H₄, B₄H₁₀= (BH)₄H₆ = C₄H₆, B₅H₉ =(BH)₅H₄ = C₅H₄, B₆H₆^2- = C₆H₂ and so on. In this regard, the observed borane structures may be considered to obey the octet rule or an equivalent noble gas configuration in the case of metalloboranes. Clearly, the fragment [BH] behaves as [C] as expected from their K values, C(K =2) and [BH], K =2.5-0.5 = 2 and in terms of equivalence in valence electron content. The major difference between the RAW SKELETAL STRUCTURE AND THE REARRANGED ONE IS THAT WHEN THE RAW STRUCTURE IS FITTED TO ITS K VALUE THE CLUSTER FORMULA IS READILY DEDUCED. HOWEVER, USUALLY THE RAW STRUCTURES OBEY THE SKELETAL VALENCES BUT DO NOT NECESSARILY OBEY THE NOBLE GAS CONFIGURATIONS. ON THE OTHER HAND, THE REARRANGED STRUCTURES DO TEND TO OBEY THE NOBLE GAS CONFIGURATION AND DEDUCTION OF THE ORIGINAL CLUSTER FORMULA IS NOT AS STRIGHTFORWARD AS IN THE RAW ONE. Another way of explaining it is to regard the [BH] fragment as a [C] skeletal element with 4 valence electrons forming the two skeletal bonds as in C₂H₄. This is indicated in F-3. The formation of 5 skeletal bonds by B₂H₆ producing a RAW SKELETAL STRUCTURE and then rearrangement to form bridged bonds illustrated simply by bonds with bridging H atoms represented as dots is also shown in F-5. The borane B₄H₁₀, can be written as (BH)₄H₆ and this corresponds to C₄H₆[K =4(2)-3=5]. If we assume that one of its isomers has a shape similar to that of B₄H₁₀, then its skeletal shape will appear as simply sketched in F-6. If we also regard the [BH] fragment to behave as [C] skeletal atom, then its structure will be comparable to that of C₄H₆ isomer shown in the same F-4. However, if we follow the skeletal valence concept of the series method, the B₄H₁₀ structure may simply be represented as in F-3 - F-5 in which the boron skeletal element exerts a skeletal valence of 5. The final structures of B₄H₁₀ and C₄H₆ are sketched and shown in F-6 to F-7 for comparison. Another good example that illustrates the concepts of SKELETAL VALENCE which immediately reveals the cluster formula and the REARRANGED ISOMERIC FORM is B₅H₉. The borane can be written as (BH)₅H₄. This corresponds to C₅H₄. Using a similar procedure as was done for B₄H₁₀, the cluster B₅H₉ (=C₅H₄) may be demonstrated in the same manner as indicated in the diagrams F-6 to F-9. Clearly, boranes may be considered to behave as HIGHLY STRAINED hydrocarbons. Hence, it is not a surprise that boranes do not occur naturally / stable in nature (only synthetic materials).

THE GOODNESS OF FIT OF K VALUE AND n SKELETAL ELEMENTS

It is extremely important that the for K(n) parameter, the skeletal linkages (K) of a cluster are drawn to fit the corresponding n skeletal elements of the cluster. Once this is done, then the ligands are added in such a way as not to violate the skeletal valences of the elements. Then the cluster formula emerges directly from the RAW SKELETAL STRUCTURE. A wide range borane-based clusters have been categorized and sketched. There are brief explanations accompanying each structure. These are shown in F-15-17, and F-19-42.

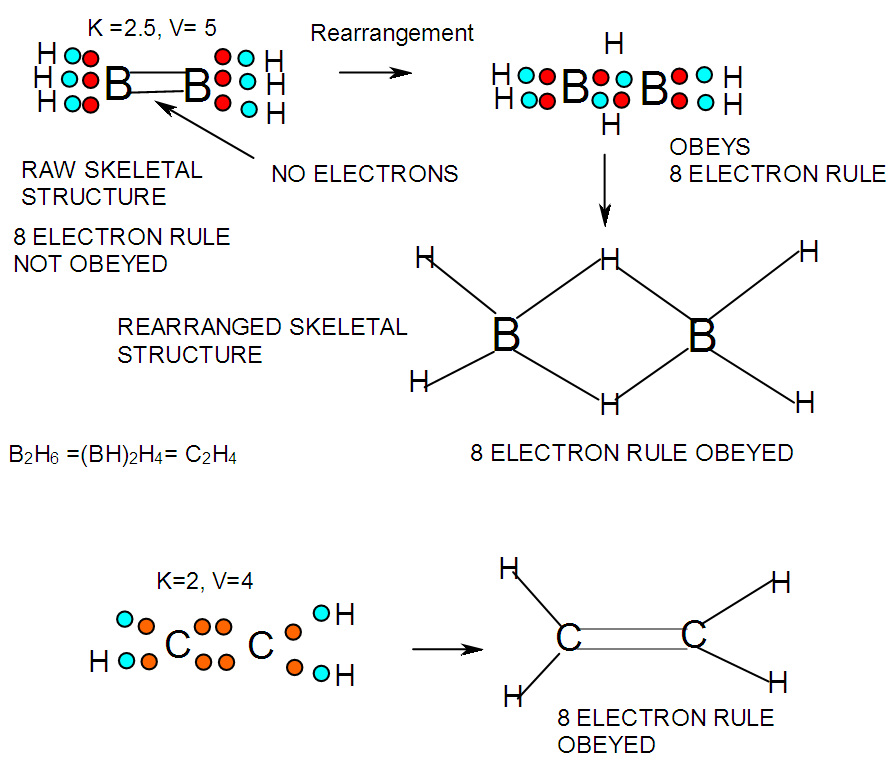F-3. Possible valence electron distribution in B2H6 and its hydrocarbon analogue C2H4

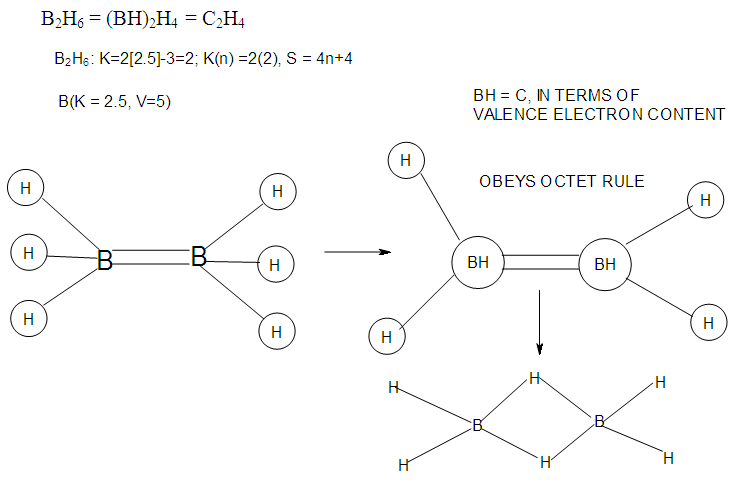F-4. Raw and rearranged structures of B2H6

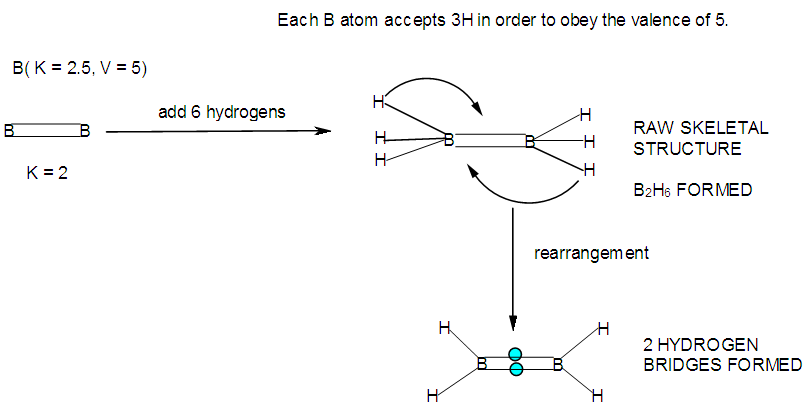F-5. Another way of showing raw and rearranged structures of B2H6

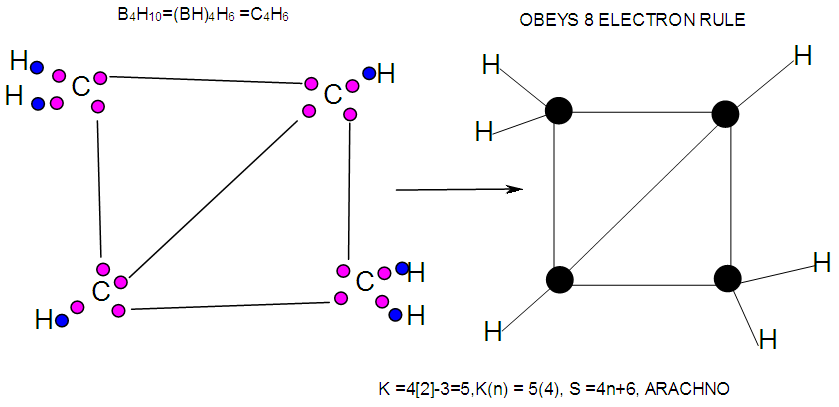F-6. Possible Valence electron distribution in C4H6 a hydrocarbon analogue of B4H10

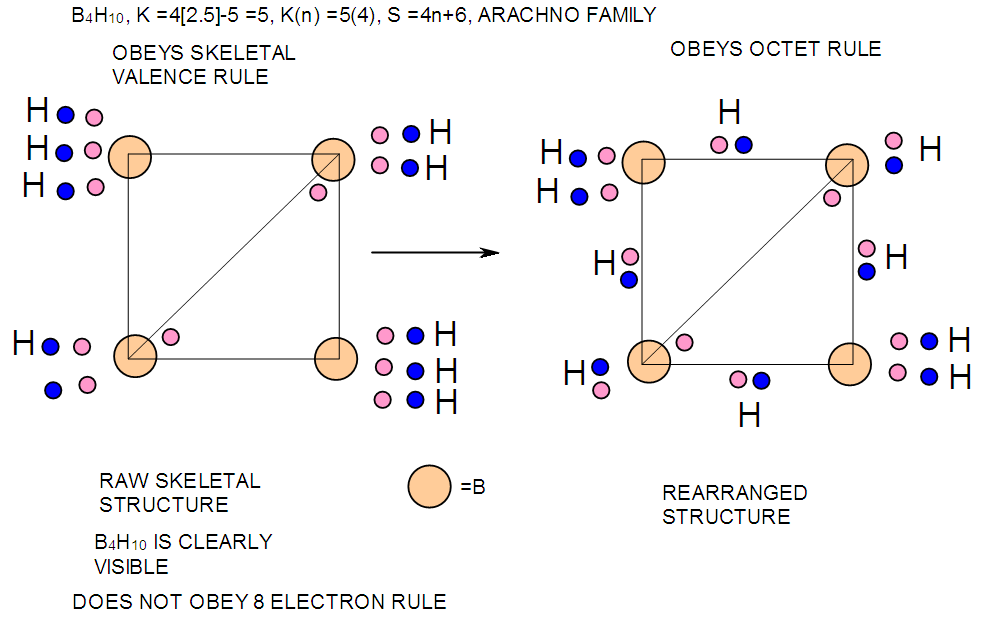F-7. Representing possible valence electron distribution in B4H10 for raw and rearranged structures

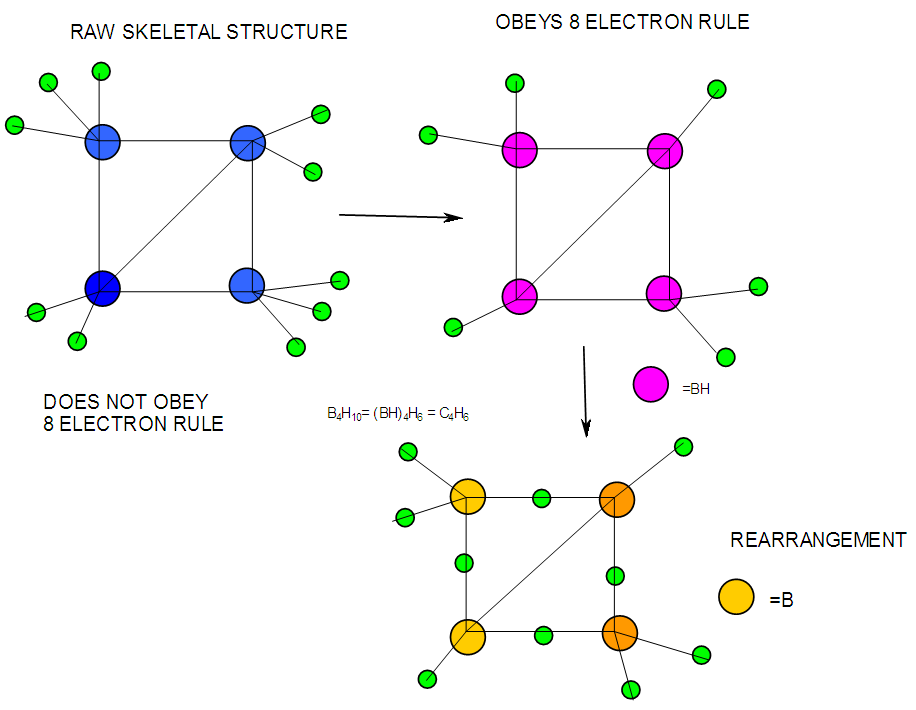F-8. Raw and rearranged structures of B4H10

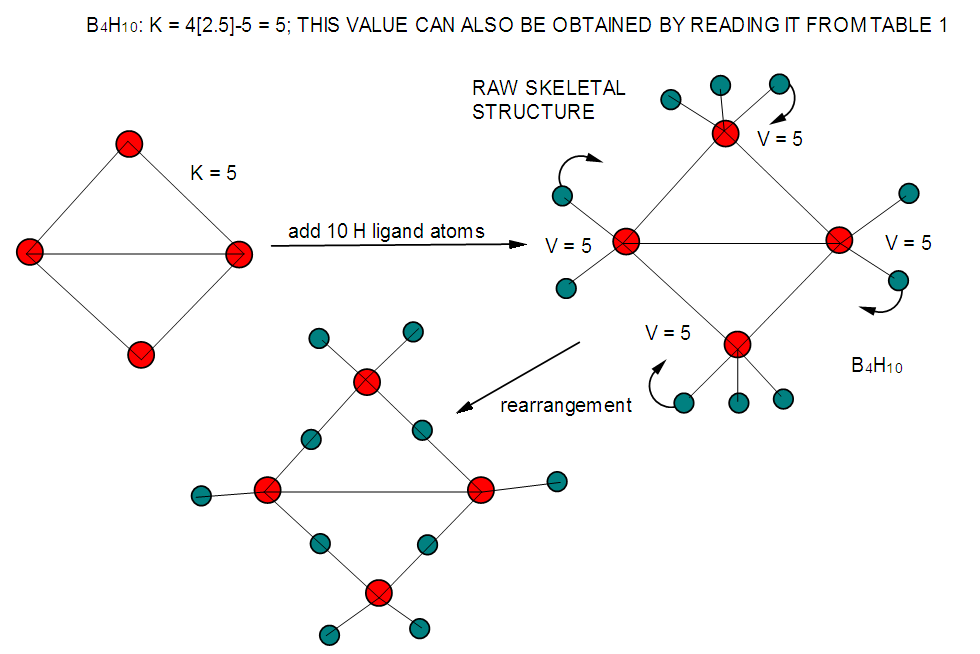F-9. Another way of presenting raw and rearranged structures of B4H10

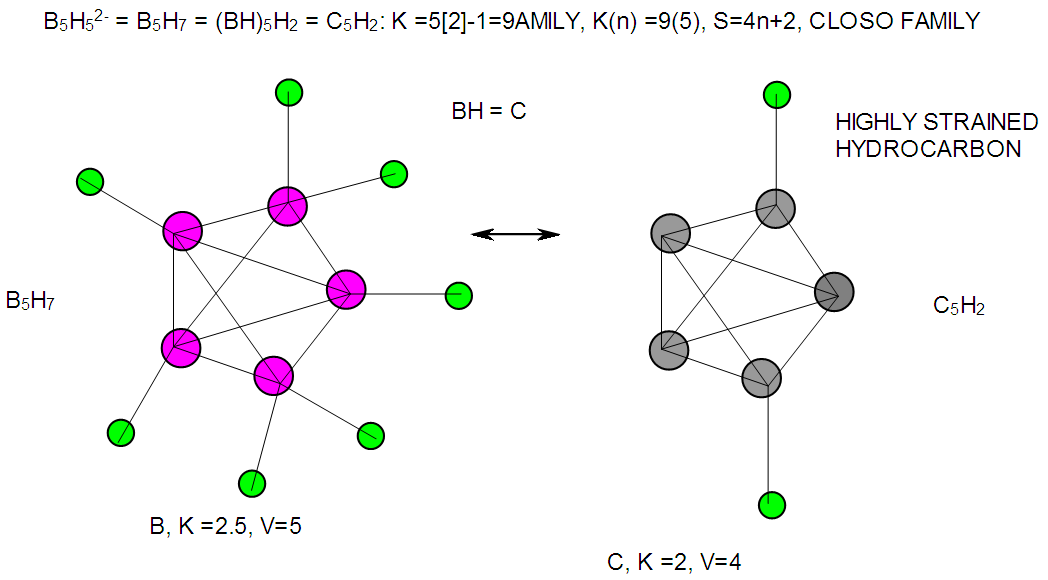F-10. Structure of B5H52- and its hydrocarbon analogue C5H2

F-11. Hydrocarbon analogue of B5H9(C5H4)

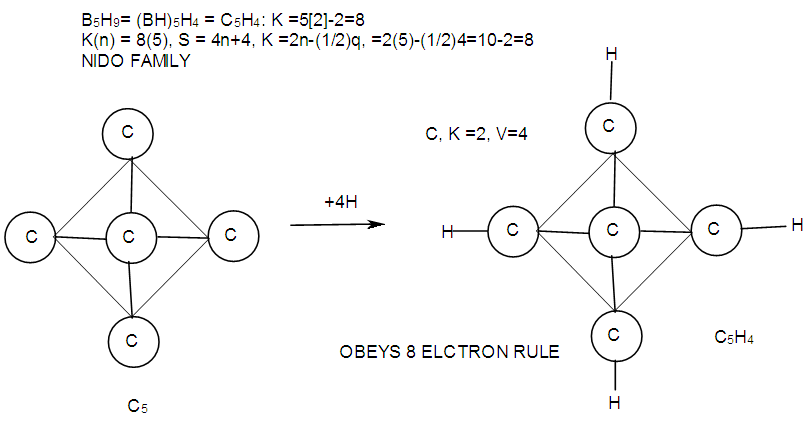
F-12. Another form of viewing the structure of B5H9

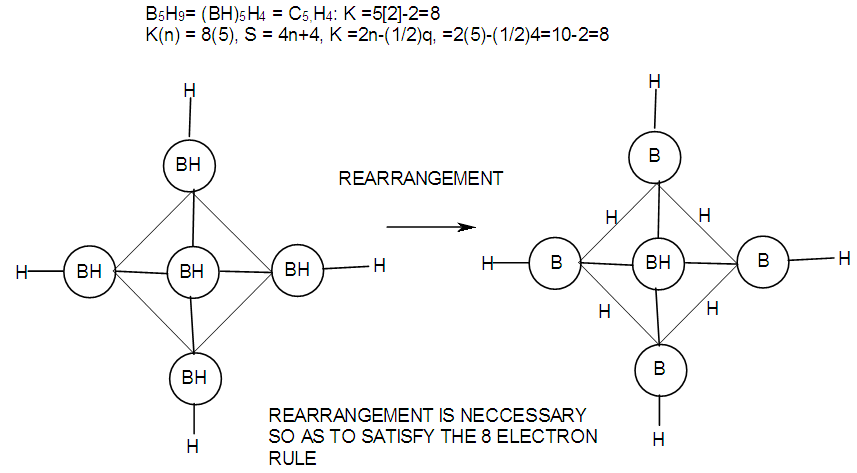
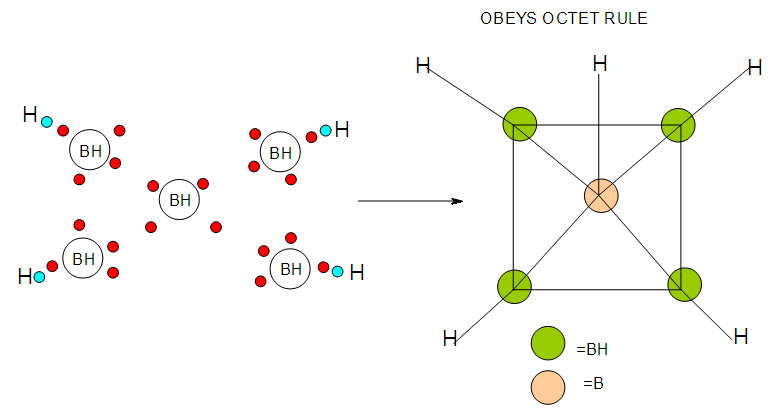F-13. Structures of B5H9 and its attempt to obey octet rule

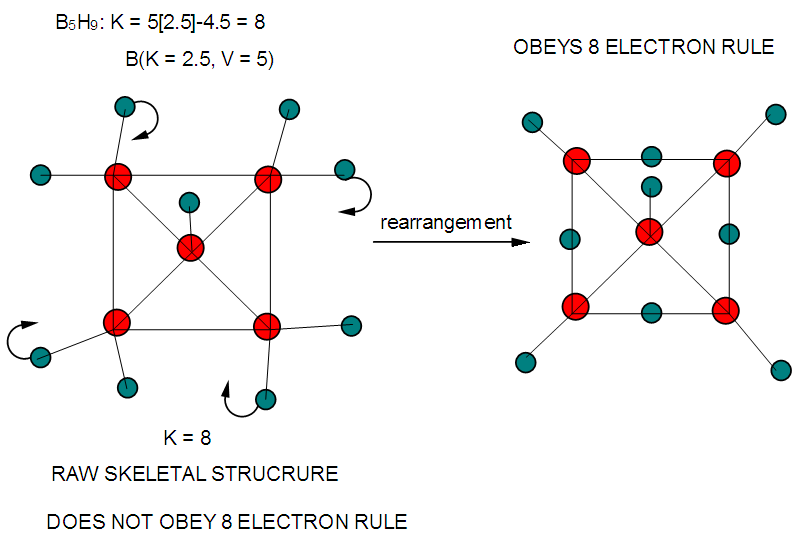F-14. Raw and rearranged structures of B5H9

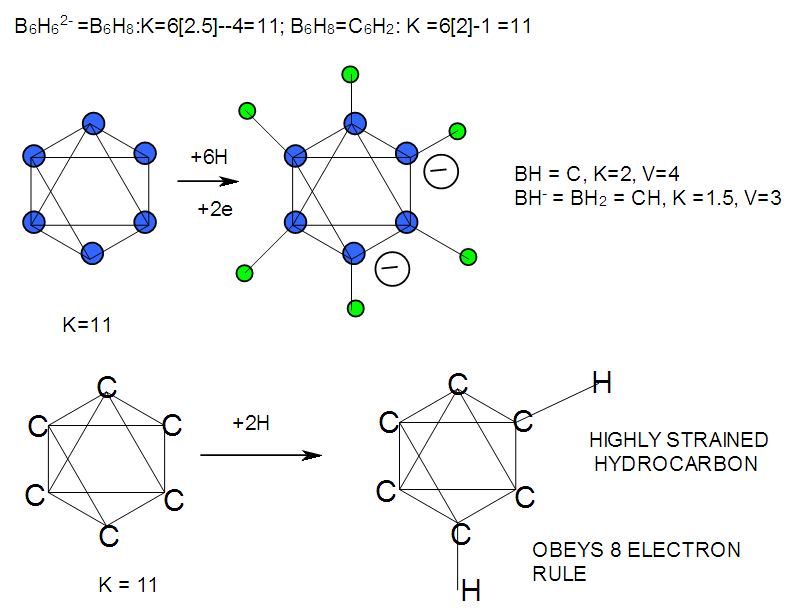F-15. Isomeric Structures of B6H62- and C6H2

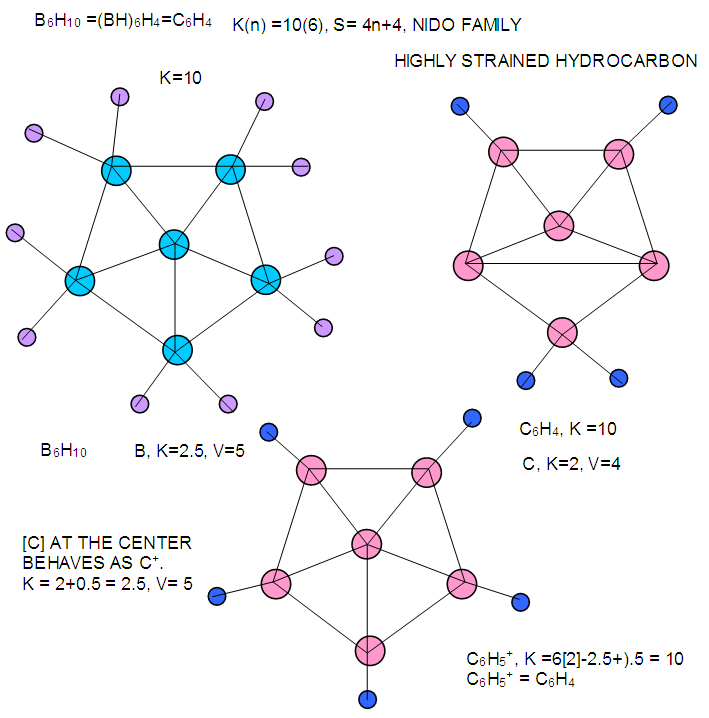F-16. Raw structures of B6H10 and comparison with isomeric structure C6H4

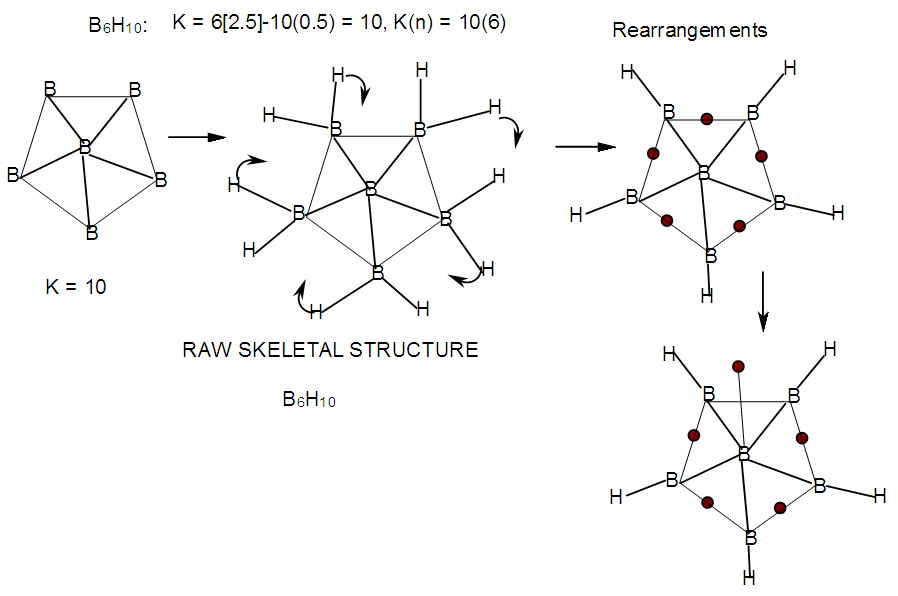F-17. Raw and rearranged structures of B6H10

The valence of 5 exerted by boron is prevalent in many borane clusters. The cluster B₄H₁₀ may also be analyzed in the same way as B₂H₆ discussed above. This is shown in Scheme F-2. As indicated in Schemes 3 - 9, the boron atom exerts a valence of 5 in its quest to obey the 8 electron rule. When the boron skeletal element interacts with another skeletal element, that element also exercises its skeletal valence. WHEN A SKELETAL STRUCTURE OF A CLUSTER IS DRAWN IN SUCH A WAY THAT ITS K VALUE MERGES WITH THE CORRESPONDING NUMBER OF SKELETAL ELEMENTS, THE CLUSTER FORMULA IS AUTOMATICALLY REVEALED.

4. Structural Framework

The building blocks of skeletal structures

As we have already discussed, the B skeletal element exerts a skeletal valence of 5(skeletal linkages) and forms various borane clusters. It has been found helpful to use structural frameworks involving 4B (square), 5B (pentagonal), or 6B (hexagonal) units as shown in Figure 18. Applying such framework structures makes it easier to draw skeletal linkages of boron clusters. The common structural frameworks are 4-1 (4 B atoms on a square with one in the middle), 4-0 (4 B atoms on a square with nothing in the middle, then 5-1, 5-0, 6-1 and 6-0. These possible structures are shown in Figure 18.

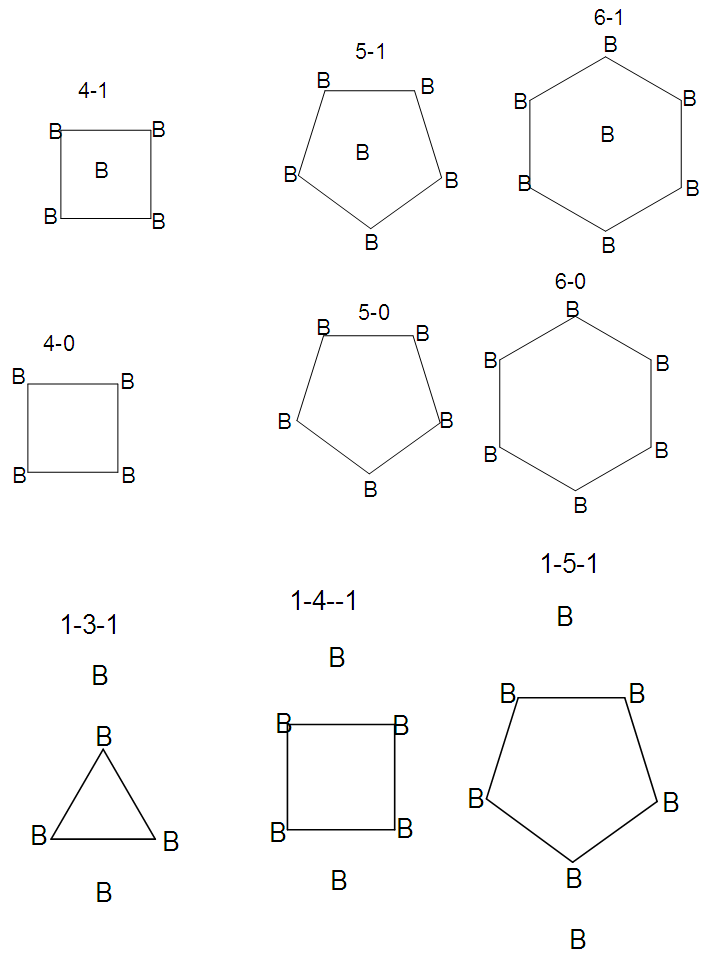Figure 18. Selected Types of Building Blocks for sketching borane structures

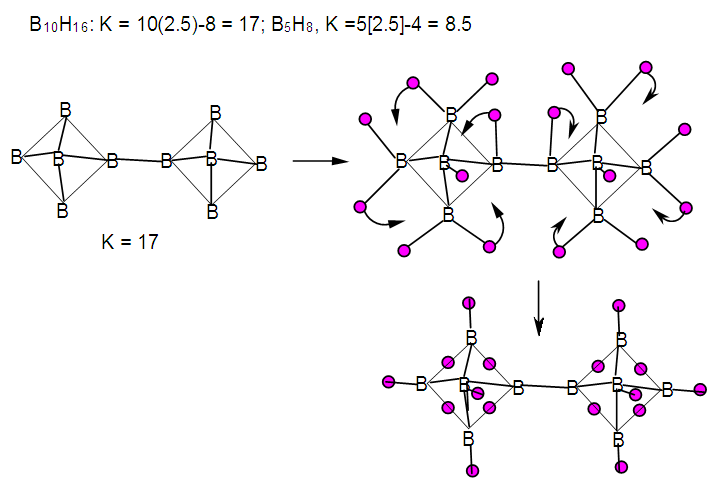F-19. Raw and rearranged skeletal structures of B10H16

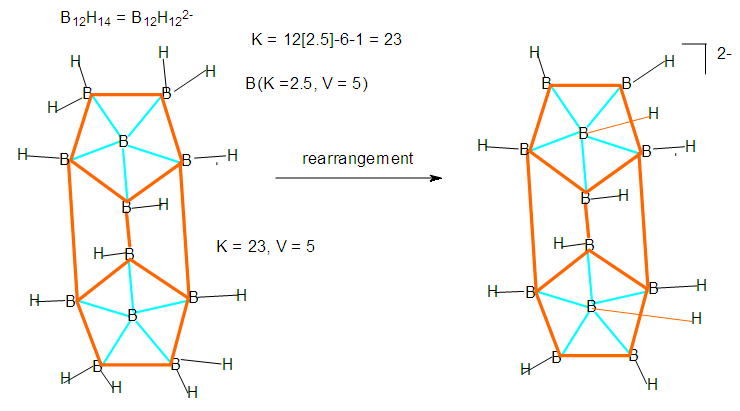F-20. Raw and rearranged structures of B12H122-

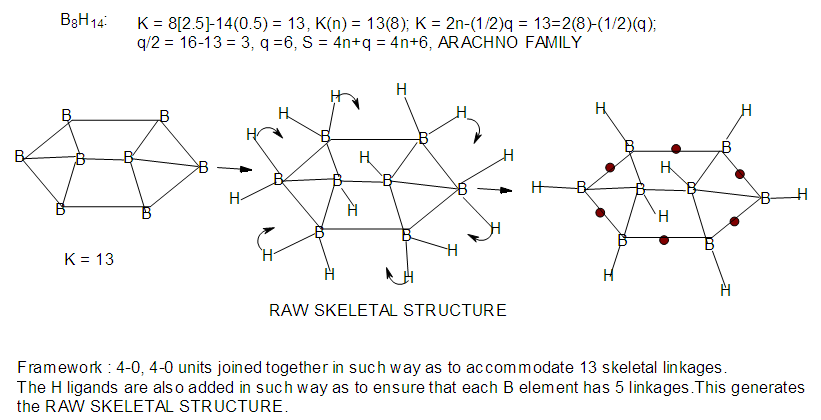F-21. Raw and rearranged structures of B8H14

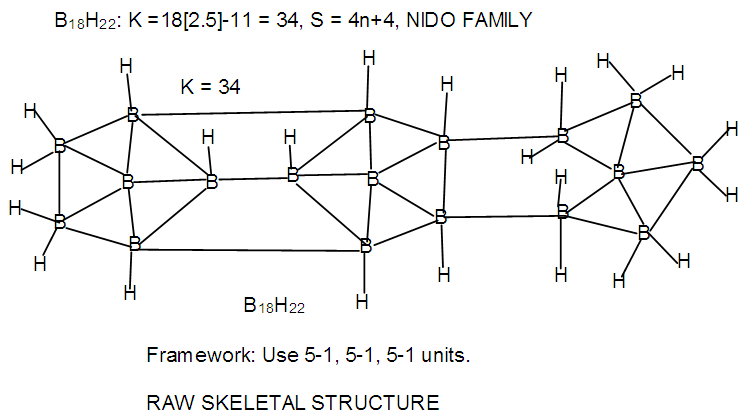F-22. Raw structure of B18H22

5. Boron Skeletal Element Interacting with Other Different Skeletal Elements

BORON WITH CARBON, PHOSPHORUS AND SULPHUR

The carbon skeletal element has a K value of 2 and valence of 4. This means that the carbon atom is allowed to exert a skeletal valence of 4 in order to attain the 8 electron rule. Hence, in constructing the RAW SKELETAL STRUCTURE of a carborane cluster, B skeletal element will still exert its skeletal valence of 5 while the C skeletal element will exert a skeletal valence of 4, phosphorus (K = 1.5) a valence of 3 and sulphur (K = 1) a valence of 2. The skeletal valences of elements from main group and transition metals are given in Tables 1 and 2. The examples:

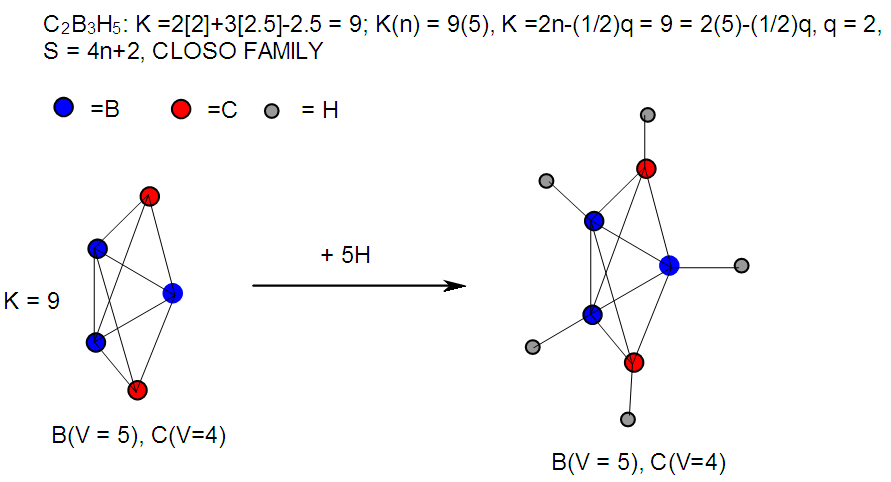F-23. Raw structure of C2B3H5

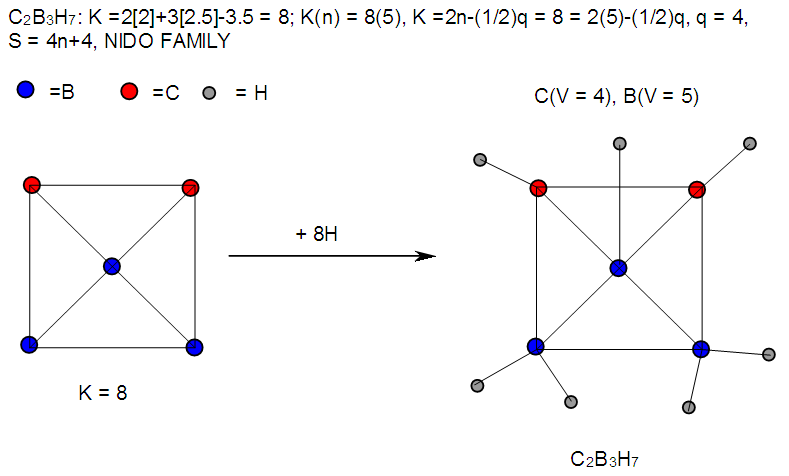F-24. Raw structure of C2B3H7

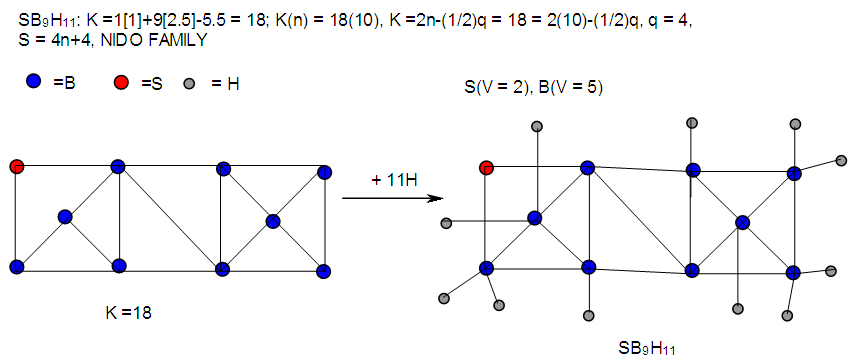F-25. Raw structure of SB9H11

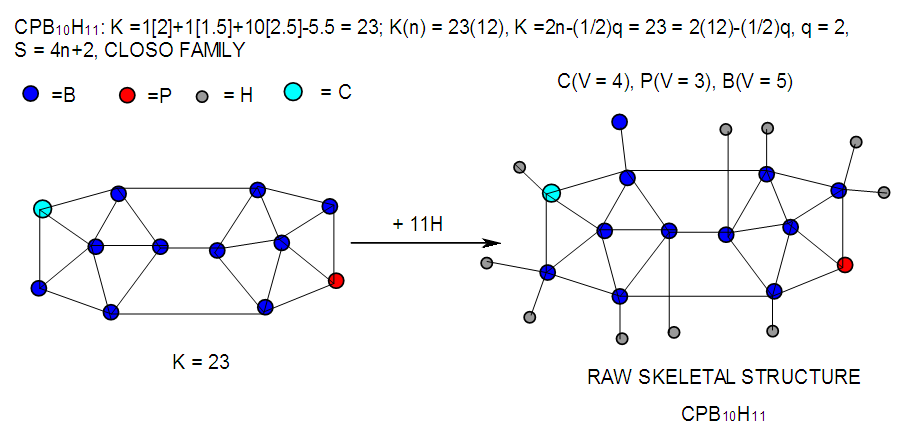F-26. Raw structure of CPB10H11

BORON WITH METALLIC FRAGMENTS

The metallic linkages in the cluster formation are related to the skeletal valences of the metallic elements. These are shown in Tables 5 and 6. In many cases the transition metals are usually associated with ligands such as carbonyls (CO) cylopentadienyl and hydrides. The ‘associate’ ligands consume some of the intrinsic linkages of the cluster elements. The remaining linkages as determined by net K value are utilized for skeletal bonding. Thus, the skeletal linkages of the metallic fragment vary depending upon the associated ligands and the type of metallic element present.

The borane clusters with metallic fragments such as (Cp*Ru)₃B₃H₈(M-1), (CuL₂)B₃H₈(M-2), and [Fe(CO)₃]B₄H₈(M-3) [23-25] assume almost the shape of corresponding boranes or heteroboranes of main group elements. If we analyze the [RuCp*] fragment using skeletal numbers, we see that its K value = 5-2.5 = 2.5. We know that [B] skeletal element has a K value of 2.5. This is the same as that of [RuCp*] fragment. From this information, it is quite clear that [RuCp*]⥈[B]. This makes the cluster (Cp*Ru)₃B₃H₈ behave as if it were (B)₃B₃H₈ = B₆H₈ = B₆H₆^2-. For the copper boron cluster (M-2), [CuL₂](K = 3.5-2 = 1.5). The K value of 1.5, means that the fragment behaves as if it were a member of group 5 elements such N, P, As, Sb or Bi (see Table 2). Thus, the cluster (CuL₂)B₃H₈ can be equated to a similar one such as (N)B₃H₈ or (P)B₃H₈ since [CuL₂] is isolobal with (M = N, P, As, Sb or Bi). Also the Fe(CO)₃ fragment has a K value = 5-3 = 2. Clearly, this is Fe(CO)₃ Hence, [Fe(CO)₃]B₄H₈ cluster can be taken to be similar to (C)B₄H₈. Similarly, for the fragment [RhCp*], K = 4.5-2.5 = 2. Therefore, [Mn(CO)₄]B₃H₈: [Mn(CO)₄, K = 5.5-4 = 1.5]; [Mn(CO)₄]B₃H₈→ (P)B₃H₈→(CH)B₃H₈→(BH₂)B₃H₈→B₄H₁₀. This relationship can also be derived from the K(n) = 5(4), K =2n- ½ q = 5= 2(4) – ½ q, q = 6 and S = 4n+6(n =4). The corresponding borane cluster can be derived from the series as follows: F_B = [BH](4) +6H = B4H₁₀. Thus, the transition metal skeletal element can literally be transformed into elements of lower K values. In a sense, it is like converting them from metallic to non-metallic fragments. Take a hypothetical example Sc(K = 7.5)→[Sc(Cp), K = 7.5-2.5 = 5→Fe]; [Sc(Cp)₂, K = 7.5-5 = 2.5→B]; [Sc(Cp)₂(H), K=7.5-5-0.5 = 2→C]; [Sc(Cp)₂(H)₂, K =7.5-5-1 = 1.5→N]. Accordingly, the skeletal linkages will change from Sc(K = 7.5, V = 15), [Sc(Cp), K = 5, V = 10], [Sc(Cp)₂, K =2.5, V = 5], [Sc(Cp)₂(H)→K = 2, V = 4] and [Sc(Cp)₂(H)₂,K = 1.5, V = 3].

The clusters, B₁₂H₁₂^2―[K = 23, S = 4n+2, K(n) =23(12), M-8] and Rh₁₂(CO)₃₀^2―( K = 23, S = 4n+2,K(n) =23(12), M-9] have been included for comparison purposes. Since the K(n) parameter for both is identical, the skeletal structures are expected to be similar. This has indeed been found to be the case [12]. The magnesium borane cluster, [Mg(B₆H₉)₂, K(n) = 24(13), S =4n+4, M-13] has a magnesium element (K = 3, V = 6), and thus it was tempting to see if the series could detect the cluster linkage of 6 for the magnesium skeletal element. The raw skeletal structure of the cluster shows that Mg exerts a skeletal valence of 6 in order for the cluster formula to be derivable. An equivalent borane cluster can be derived from the series S = 4n+4(n = 13), F_B= [BH](13)+4H = B₁₃H₁₇.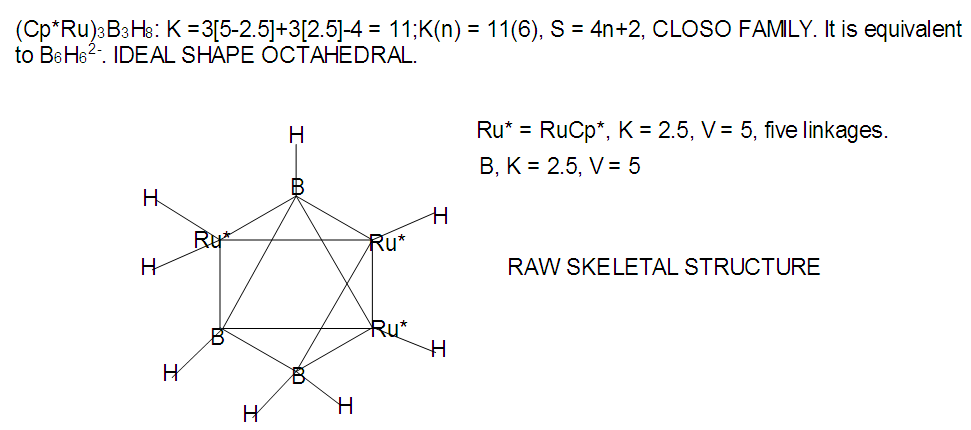

F-27. Raw skeletal structure of (Cp*Ru)3B3H8

In this example, the [RuCp] has a K value given by K = 1[5-2.5] = 2.5. Hence its valence is 5. This means it is allowed to have 5 linkages. In actual fact, [RuCp] ⥈ [B].

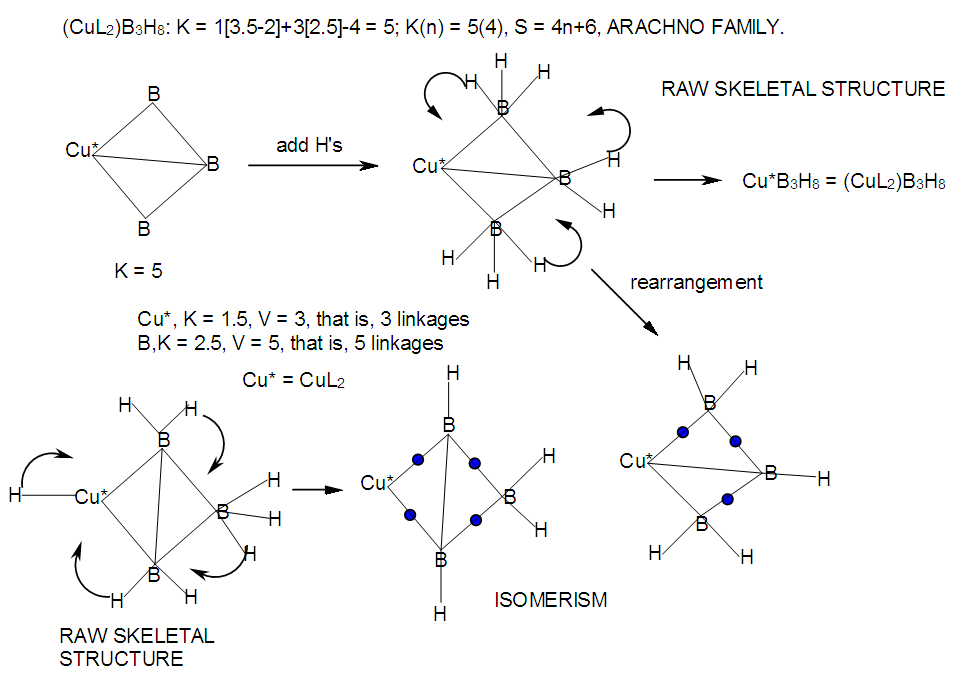M-28. Raw skeletal structure of (CuL2)B3H8

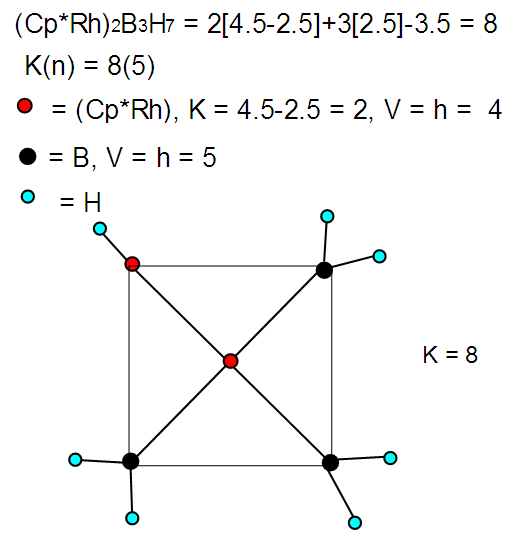M-29. Raw skeletal structure of (Cp*Rh)2B3H7

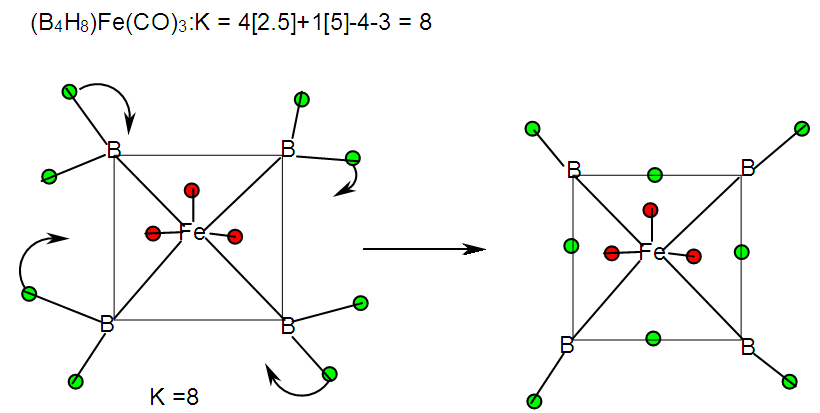F-30. Raw skeletal structure of [Fe(CO)3]B4H8

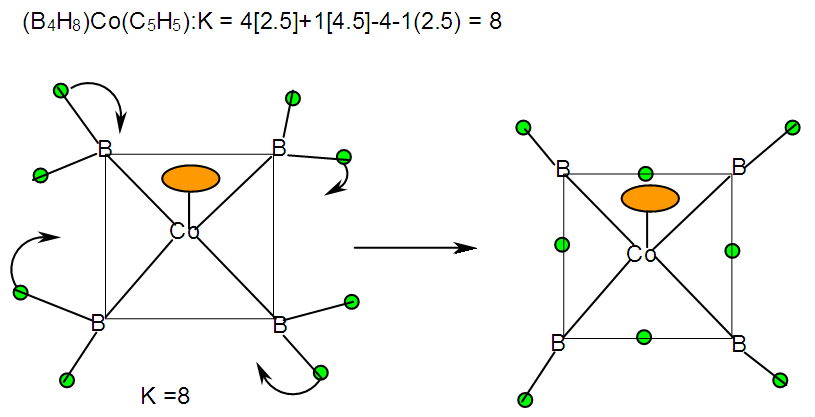F-31. Raw skeletal structure of (CpCo)B4H8

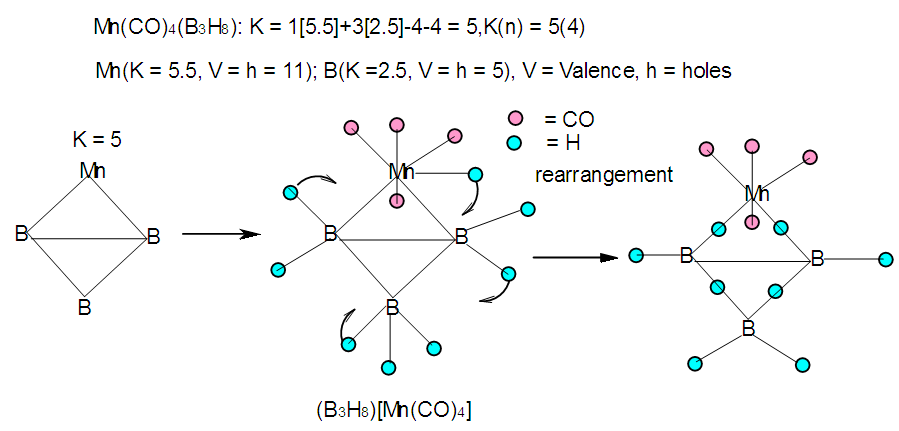F-32. Raw skeletal structure of [Mn(CO)4]B3H8

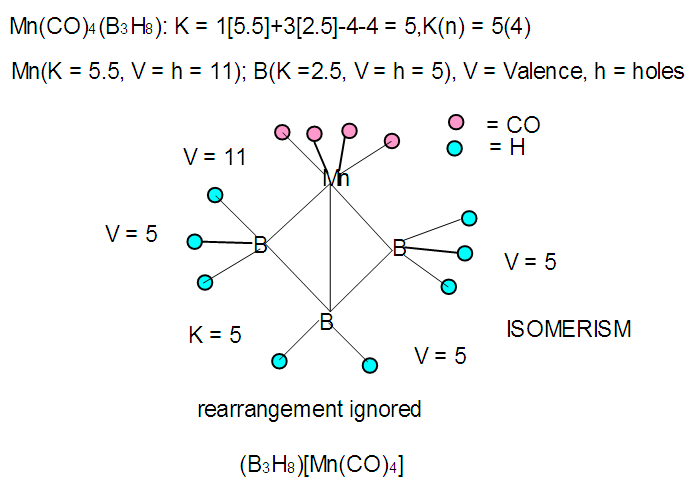F-33. Isomer of [Mn(CO)4]B3H8

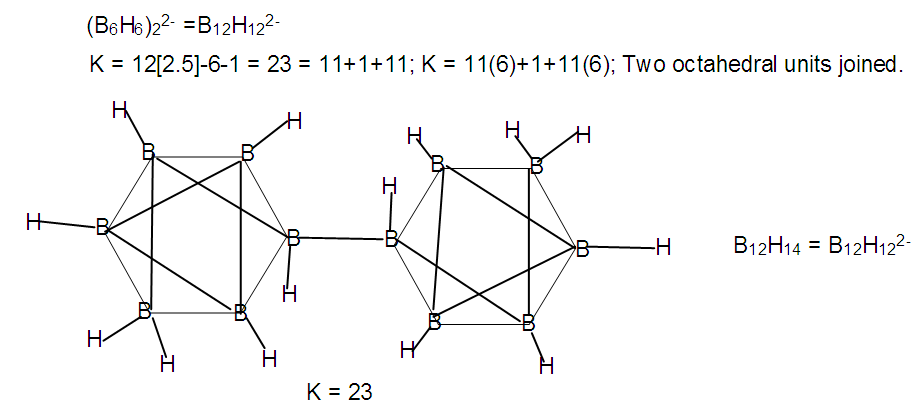F-34. Raw skeletal structure of B12H122-

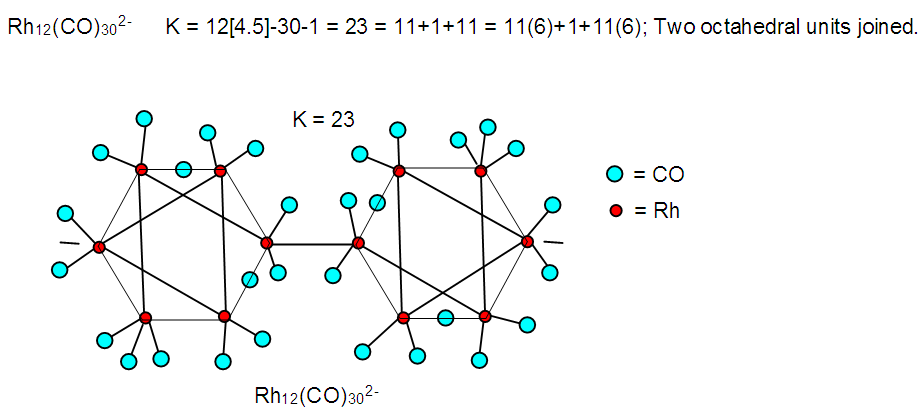F-35. Skeletal structure of Rh12(CO)302―

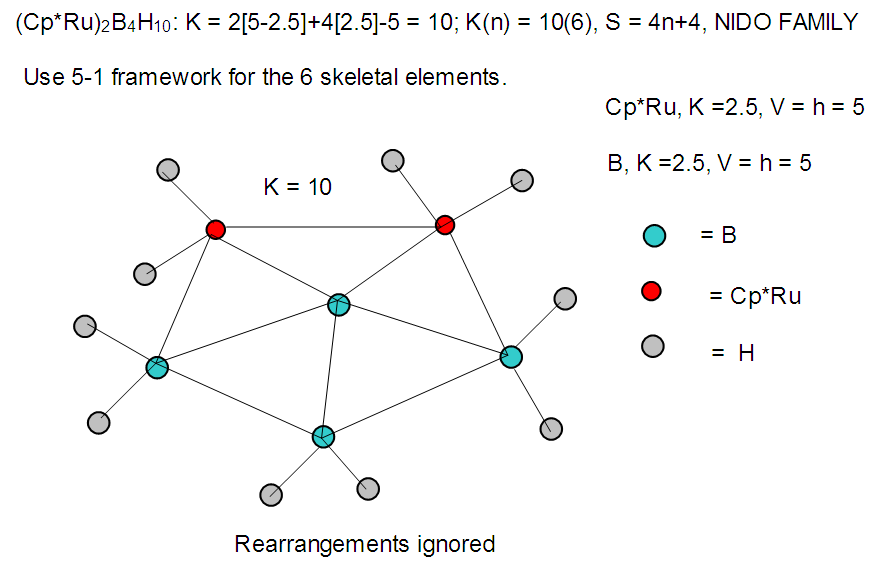F-36. Raw skeletal structure of (Cp*Ru)2B4H10

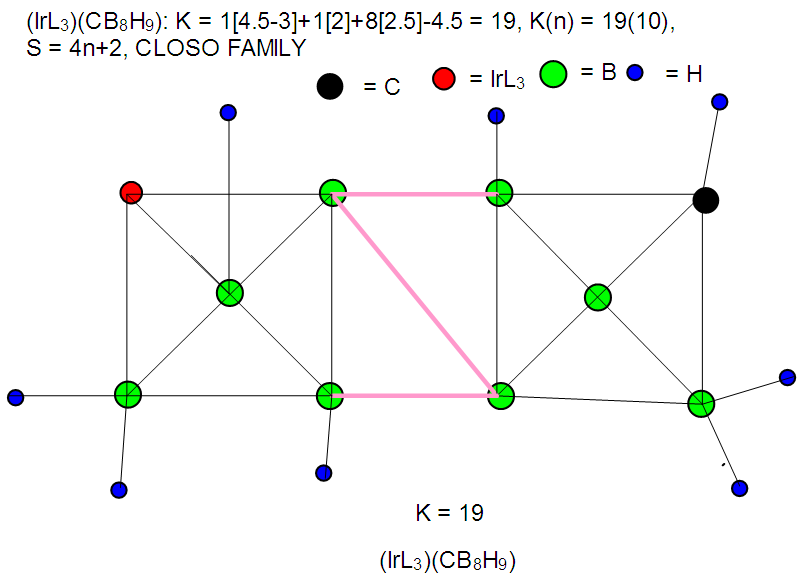F-37. Raw skeletal structure of (IrL3)CB8H9

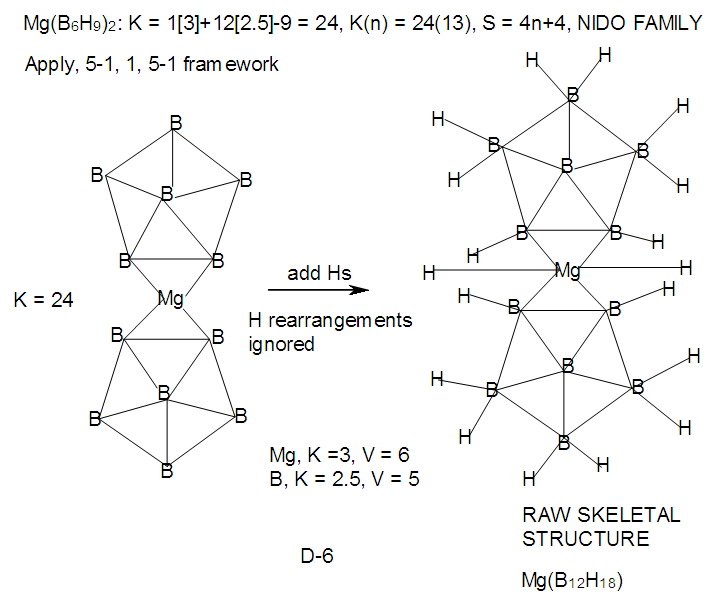F-38. Raw skeletal structure of Mg(B6H9)2

6. The Variation of Linkages with Ligand Electron Density

According to the series method, the clusters form according to the valences or linkages of skeletal atoms and fragments. Thus, in the case of boranes, the boron atom itself has a K value of 2.5 and a valence of 5. This means that a single atom on its own is allowed to have 5 lines connected to it. On the other hand when it is bound to a hydrogen atom to form a [BH] fragment, it is allowed to be linked to 4 lines. This is due to K value of [BH] fragment given by K = 1[2.5-0.5] = 2 and its corresponding valence V = 2x2 = 4. Similarly, a [BH₂] fragment will have K = [2.5-2(0.5)] = 1.5, and V = 3 (three linkages). Accordingly, [BH₃] has 2 linkages, [BH₄^―] one linkage and BH₅ or BH₄^―, zero linkages. This is illustrated in Scheme 1. The shape of the unstable BH₃, the hypothetical BH₅ and the stable and known boron complex BH₄^― are shown in A-1. Selected examples showing the allowed linkages of skeletal elements and fragments are given in Tables 5 and 6.

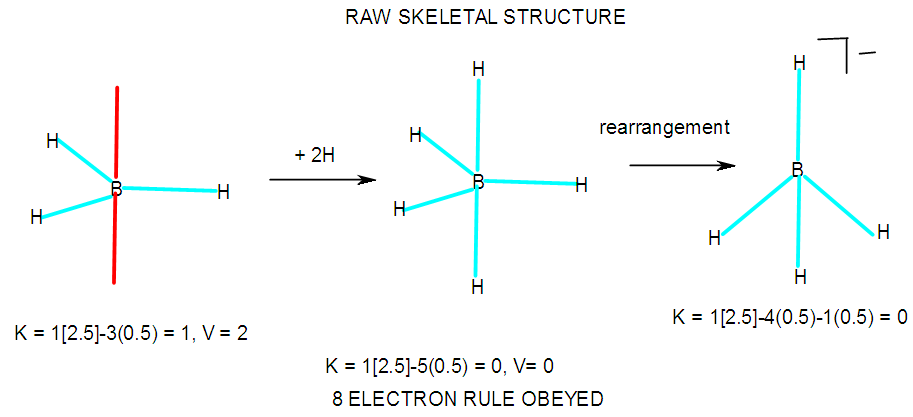F-39. An illustration between skeletal linkages and fragment

Just as the addition of H ligands stepwise to the [B] skeletal element as in Scheme 4 reduces the K value by 0.5 and hence the number of skeletal linkages of the [B] skeletal element by 1, the addition of ligand(s) to metallic skeletal element reduces its linkages according to the number of electrons donated by the ligand(s). Take the case of Re (K = 5.5, V = 11); it has 11 skeletal linkages. When a hydrogen ligand [H] is added to [Re], the fragment [ReH] is formed with K = 5.5-0.5 = 5 and the valence (linkages) become 10. On the other hand when cyclopentadienyl fragment is added to produce [(η⁵-C₅H₅)Re = CpRe] fragment, K = 5.5-2.5 = 3 and hence V = 3x2 = 6. In principle, the products of the following hypothetical reactions CpRe + 6H→ CpReH₆; CpRe +C₆H₆→ [(η⁵-C₅H₅)Re(η⁶-C₆H₆] can be predicted to be formed. If we take the fragment [CpM] keeping the ligand Cp constant and varying M, the skeletal fragment linkages of M will be reduced by K = 2.5 or V = 5. For instance, [CpFe], K = 5-2.5 = 2.5, V = 5; [CpCo], K = 4.5-2.5 = 2 and V = 4 and [CpNi], K = 4-2.5 = 1.5, V = 3.

The chemical species BH₆⁺, BH₇²⁺, BH₈³⁺, CH₅⁺, CH₆²⁺, CH₇²⁺, NH₅²⁺, OH₄²⁺, C(AuL)₆²⁺, N(AuL)²⁺ and O(AuL)₄²⁺ have recently been studied [24]. Also OH₃⁺ is a well-known ion. With the help of series we may be able to explain their possible occurrence as shown in Scheme 7. We can identify the central skeletal element and assign a charge to it. The next step is to assign a K value and skeletal valence to it. The skeletal valence will correspond to the number of fragments it will combine with. For instance, [B] has K = 2.5 and V = 5. This means it will bind 5H ligands while B⁺(K = 3, V = 6) will bind 6H and B²⁺(K = 3.5, V = 7) will combine with 7H ligands. Finally, B³⁺(K = 4, V = 8) will take 8H ligands. Other clusters may similarly be explained as illustrated in Scheme 4. The scheme also demonstrates how the skeletal linkages vary with the change of electron density around the central skeletal element. In the case of the boron fragments (Scheme 4), we have B(K = 2.5, V = 5)→BH(K = 2, V = 4)→BH₂(K = 1.5, V= 3)→BH₃(K = 1, V = 2)→BH₄(K = 0.5, V = 1) and BH₅(K = 0, V = 0).

Scheme 7. An illustration between skeletal linkages and the charge variation on skeletal fragment

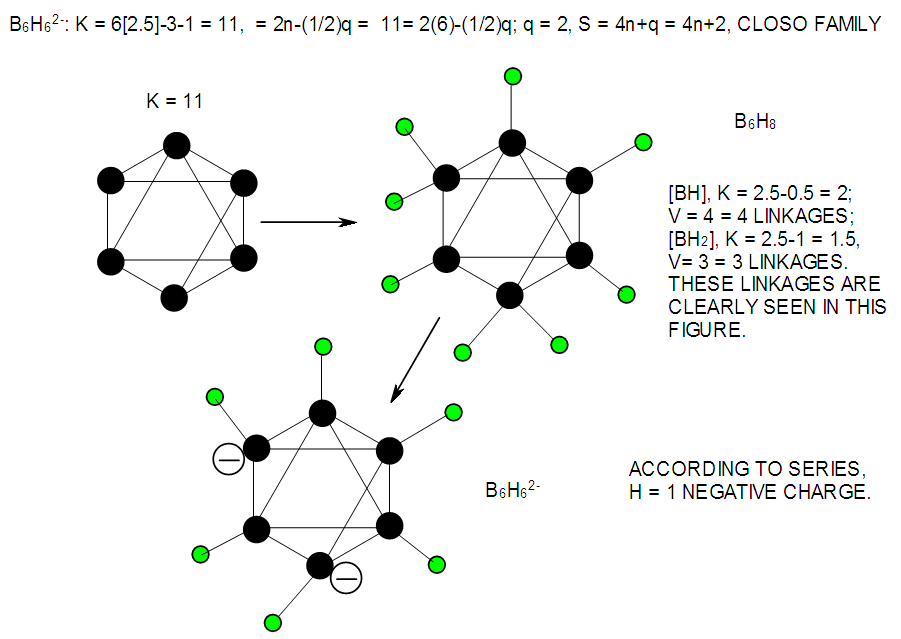F-40. Raw and rearranged skeletal structures of B6H62―

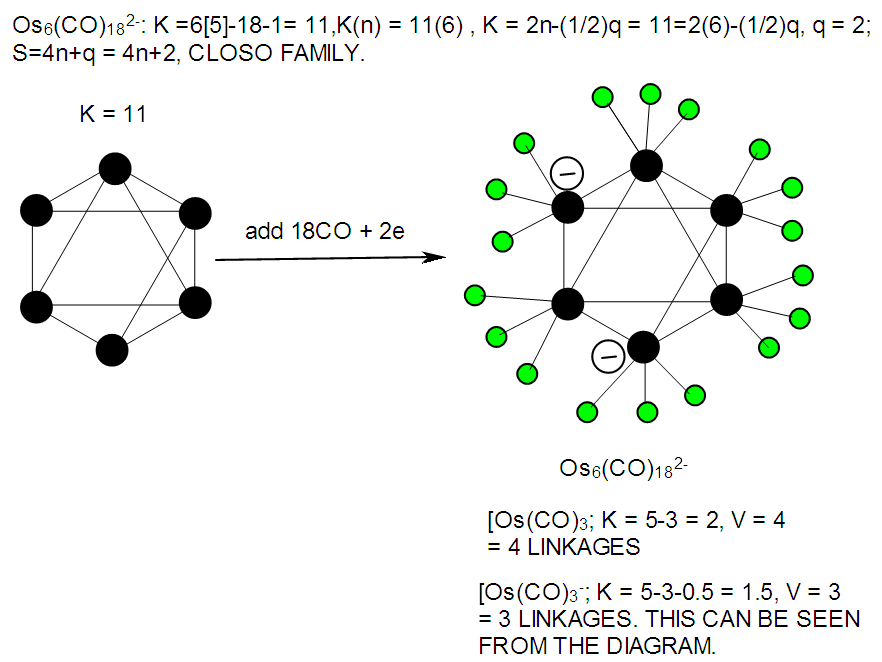F-41. Raw skeletal structure of Os6(CO)182―

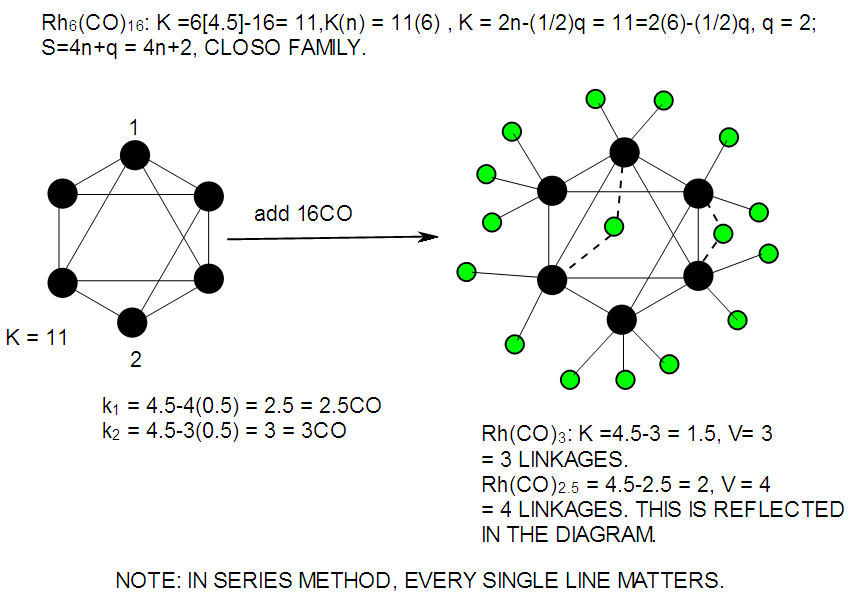F-42. Raw skeletal structure of Rh6(CO)16

It is quite clear from the above diagrams in A-2 to A-4 that the linkages and the corresponding K values of the fragments reflect that there is isolobal relationship among fragments. Thus, [Rh(CO)_2.5]⥈[Os(CO)₃]⥈[BH]; K =2, V = 4 and [Rh(CO)₃]⥈[Os(CO)₃^―]⥈[BH₂]; K = 1.5, V = 3.

7. Conclusions

Skeletal numbers and their valences are extremely useful in the construction of raw skeletal shapes of chemical clusters. Such structures confirm or verify the formulas of respective clusters. The skeletal shapes of clusters with nuclearity N₁ to N₁₂ or moderately higher are easily constructed with the help of skeletal numbers and their respective valences. The skeletal valences are linked to the hole formalism associated with the 8 or 18 electron rule. The unification of cluster linkages and the number of skeletal elements (n) taking into account the type of series makes it easier to assign the number of ligands to a skeletal element. The number of skeletal linkages on skeletal elements varies depending upon the number and type of ligands attached to it. Due to the simplicity of the method, a large number of boranes and related clusters have been analyzed and presented so as to enable the readers to experience the viability and flexibility of the 4n series method. It is also interesting to note that all borane formulas could readily be derived from a PRINCIPAL MONO-SKELETAL FRAGMENT [BH].

ACKNOWLEDGEMENTS

I wish to acknowledge Dr. Penelope Emma Tukasingura Kiremire for editing the draft paper and Mrs Merab Kambamu Kremire for her encouragement to write the paper and founding Yowasi Kiremire Memorial University of Applied Sciences on Shumba Hill in Bwanga, Rukungiri, Western Uganda.