1. Introduction

Numerical characterization of borane clusters with STYX numbers was initiated by Lipscomb in 1976 [1]. Subsequently, Wade-Mingos rules based upon molecular orbital theory were introduced [2-8]. More recently, the 14n series method has been introduced to categorize clusters and fragments of transition metal carbonyl clusters [9]. The 14n method was discovered by simply analyzing the pattern of osmium carbonyl clusters [10]. The series S = 14n+q was derived as an answer to a question as to whether the osmium carbonyl clusters occur in a random or an organized orderly fashion [10]. The revelation occurred when it was found that an osmium carbonyl fragment [Os(CO)₃] could be utilized to generate the formulas of all the osmium carbonyl clusters encountered [10]. More importantly, it was remarkable to discover the term T = 14n(n = 1, 2, 3, ..) could result in the same figure as the valence electrons of the cluster series S = 14n+0. For instance, Os(CO)₃,V = 14, Os₂(CO)₆, V = 28, Os₃(CO)₉, V = 42, Os₄(CO)₁₂, V = 56, Os₅(CO)₁₅, V = 70, Os₆(CO)₁₈, V = 84 , and so on. This type of cluster series was assigned the series formula S = 14n+0. Further reflection revealed that if we add a CO ligand to Os₆(CO)₁₈, we get Os₆(CO)₁₉,V = 84+2 = 86. Thus, Os₆(CO)₁₉ could be assigned the series symbol, S = 14n+2. On the other hand, the cluster, Os₆(CO)₁₈ (S = 14n+0)-CO = Os₆(CO)₁₇ (V = 84-2 = 82) could be assigned the cluster series symbol, S = 14n-2. In other words, the Os₆(CO)₁₈^2― cluster which is isoelectronic with Os₆(CO)₁₉ also belongs to S = 14n+2 series [11]. The detailed process of developing the 14n+q/4n+q series as well as the empirical formula K = 4n- ½ q can be found in previous work [9]. Hence, categorization of clusters was based on utilizing fragments with valence electron content of (14) such as [Os(CO)₃], [RhH(CO)₂], and [ReH(CO)₃], for categorization of transition metal carbonyl clusters and the (4) electron fragments such as [C], and [BH] for hydrocarbons, boranes and carboranes and so on for main group elements. After further discovery of the isolobal relationship, S = 14n+q ⥈ S = 4n+q, it was proposed to use the 4n+q series term to categorize and characterize clusters as it was easier and less cumbersome. However, when calculating the valence electron content of a transition metal fragment or cluster, it is inevitable that we use the 14n+q formula. Arising from the 4n series method, skeletal numbers have been discovered and these have been found to be exceedingly useful as they are more precise in categorizing and analyzing fragments, molecules and clusters [12-14]. The series method can simply be regarded as a ‘deaf and dumb’ guide in the world of clusters. What needs to be done is to put a chemical sense on what the series method tells us. By applying skeletal numbers, we can rapidly analyze, categorize and characterize fragments, molecules, clusters, and ligands numerically. In this paper, the meaning of skeletal numbers will be defined and their application to generate cluster trees and series will be explained.

2. Results and Discussion

2.1. A General Concept of the Skeletal Numbers and Their Interpretation

On a deeper level of analysis of the series method results especially the skeletal numbers, it has been revealed that the skeletal numbers may be regarded as representing the shortage of electron pairs required by the skeletal element(s) in a fragment or cluster for it (them) to obey the 8 or 18 electron rule. The skeletal numbers were derived using the 4n series method* and are provided in Tables 1-3 for ease of reference and interpretation purposes. If we take lithium Li a member of group 1 elements, it has a K value of 3.5. That means it has a deficit of 3.5 electron pairs, that is, 3.5x2 = 7 electrons in order for it to obey the 8 electron rule. This applies to all group 1 elements. Likewise, the carbon atom with a K value of 2 has a shortage of 2 electron pairs (4 electrons) for it to observe the 8 electron rule, which is why it can form molecules such as CH₄, CO₂, and CF₄ in order to satisfy the requirement. On the other hand, N(K = 1.5) will need 3 electrons and that is why it can form a nitride ion, N^3―, and molecules such as NH₃, and HNF₂. C₂ (K = 4) will need 4 electron pairs, thus 8 electrons to form C₂ ^8― [ = 2 C^4―] or 8 hydrogen atoms to form C₂H₈ [ = 2CH₄]. If we assume that the process occurs stepwise by receiving one electron pair in the form of hydrogen atoms at a time, then C₂+2H →C₂H₂(K = 3). This means that the C₂H₂ (K = 3) molecule requires 3 electron pairs in order for the carbon skeletal elements to achieve the 8 electron rule. If the C₂H₂ molecule gets another 2 electrons from two more hydrogen atom carriers, then we get C₂H₂+2H → C₂H₄ (K = 2). The molecule C₂H₄ (K = 2) has a deficit of 2 electron pairs for the 2 skeletal elements to achieve the octet rule. If it receives 2 more hydrogen atoms, we will get C₂H₆(K = 1). This tells us that the C₂H₆ molecule still has a deficit of 1 electron pair for the two carbon atoms to attain the 8 electron rule. This implies that if we add two more hydrogen atoms as electron carriers or even 2 electrons to C₂H₆, then the 2 carbon atoms will meet the 8 electron rule requirements. We can represent the transformation by a simple equation, C₂H₆ +2H →C₂H₈ → 2CH₄ or C₂H₆ +2e →C₂H₆^2― → 2CH₃^―. The transformation of C₂ to CH₄ or CH₃^― or C^4― is a simple hypothetical illustration of the interpretation concept that could be assigned to the K parameter. The K values in Tables 1 and 2 or wherever they are found, may be interpreted in the same way. This concept also applies to transition metal complexes. For instance, (C₂H₄)(CO)PdCl₂ complex has a K value given by K = 1[4]-1-1-1 = 1. This means the complex is lacking one electron pair to achieve 18 electron configuration. So we expect it to try to attempt adding 2 electrons in one form or another especially adding on another ligand such as CO to form (C₂H₄)(CO)₂PdCl₂ complex. Similarly, Fe₂(CO)₉ complex which also has a K value of 1 given by K = 2[5]-9 = 1 will try to do the same; that is, Fe₂(CO)₉ + CO→Fe₂(CO)₁₀ which decomposes into 2 [Fe(CO)₅] mono-skeletal units. Take the case of Rh₂(Cp)₂(CO)₂, with K =2[4.5]-2(2.5)-2(1) = 2, implying it has a shortage of 2 electron pairs in order for its skeletal atoms to achieve the 18 electron rule. Hence, if we donate 2CO ligands to it, it will decompose into 2 complexes each of which will obey the 18 electron rule. Thus, Rh₂(Cp)₂(CO)₂ + 2CO→2[Rh(Cp)(CO)₂]. Take the example of Mo₂(Cp)₂(CO)₄,K =2[6]-2(2.5)-4 = 3: this complex has a shortage of 3 electron pairs. Assuming that these will be contributed by 6H atoms, then we can express this as Mo₂(Cp)₂(CO)₄+6H→ Mo₂(Cp)₂(CO)₄(H)₆→2[Mo(Cp)(CO)₂(H)₃]. Alternatively, we could have Mo₂(Cp)₂(CO)₄ + 2CO+2H→ Mo₂(Cp)₂(CO)₆(H)₂→2[Mo₂(Cp) (CO)₃(H)]. Take the example of P₄ (K = 4x1.5 = 6]. This cluster has a shortage of 6 electron pairs. Let us assume these are donated by H atoms, then P₄ + 6x2H→ P₄H₁₂→4[PH₃]. The same applies to Ir₄(CO)₁₂,K = 4[4.5]-12= 6. We can set up a simple hypothetical equation as follows: Ir₄(CO)₁₂+4CO+4H→ Ir₄(CO)₁₆(H)₄→4[Ir(CO)₄(H)]. Let us consider two more examples in this section as more examples are provided in the rest of the paper. Os₅(CO)₁₆, K = 5[5]-16 = 9. This means, if we could for example add more 9CO ligands to the cluster, the entire cluster will obey the 18 electron rule and will then decompose into mono-skeletal fragments. Thus, Os₅(CO)₁₆ + 9CO→ Os₅(CO)₂₅→5[Os(CO)₅]. As we know well, Os(CO)₅ complex obeys the 18 electron rule. The last one is Sn₅^2―, K = 5[2]-1 = 9. So we also need 9 pairs of electrons. Hence, we can do this by adding 9 electron pairs in the form of H atoms. Thus, Sn₅^2― + 9x2H→Sn₅H₁₈^2―→ Sn₅H₂₀→5[SnH₄].

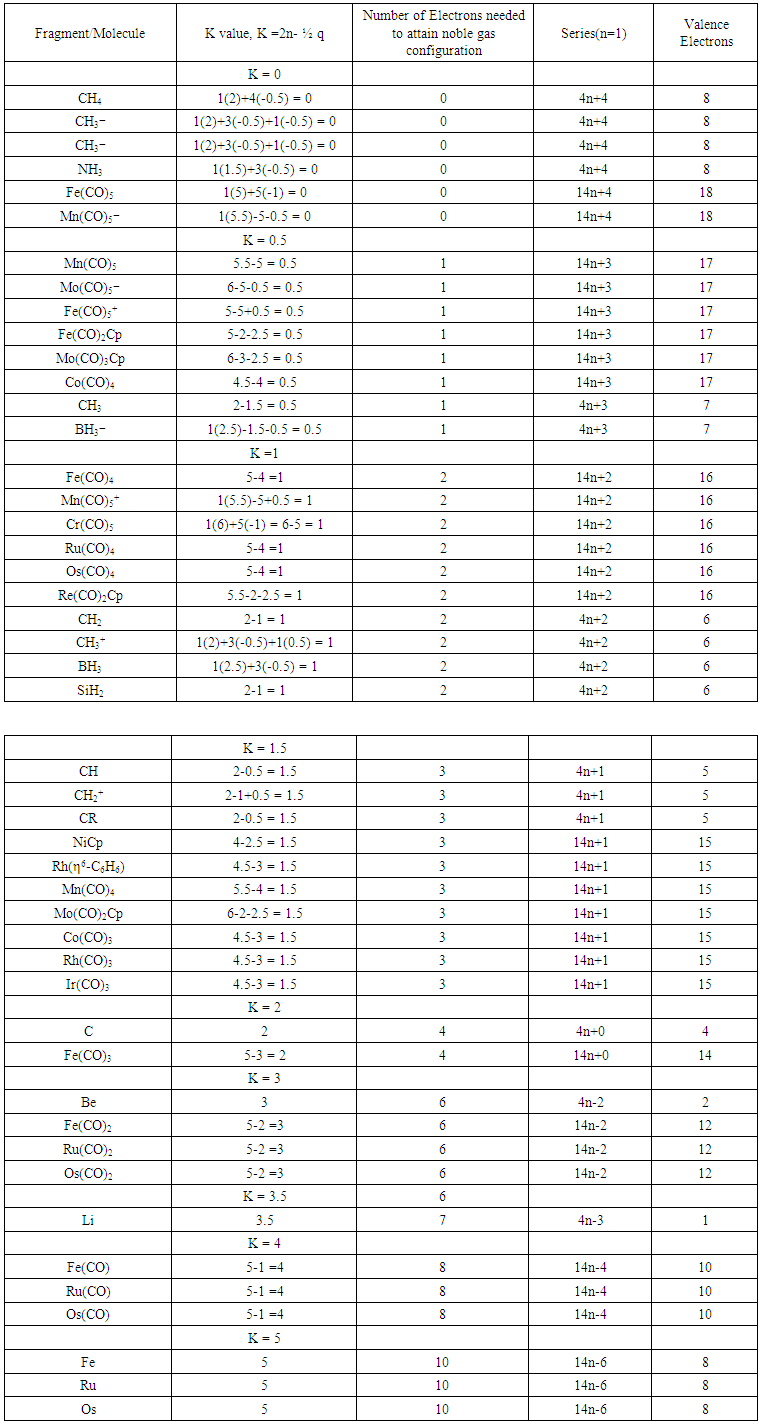
2.1.1. The 8 Electron Rule (see Table 1)

The skeletal number K for the boron atom is 2.5 (Table 1). This means that it requires 2.5 electron pairs, that is, 2.5x2 = 5 extra to satisfy the eight (3+5 = 8) electron rule. This applies to all the remaining elements of group 3 (or 13). Likewise, the lithium element Li, has a K value of 3.5. According to the series approach, this means it requires 3.5 electron pairs or simply 7 electrons so as to obey the octet (1+7 = 8) rule. This also applies for all members of group 1 elements. For group 7 members K = 0.5. These just need only one electron so as to obey the octet rule. It is obvious that group 8 elements will need nothing and hence, K = 0. Thus, the skeletal numbers of skeletal elements from groups 1 to 8 can be translated in the same way.

The calculation of the cluster number K value was explained in earlier work [12-14]. The aim of this paper is to re-emphasize the meaning that could vividly be attached to the K values, that is, ‘ELECTRON PAIR(s) DEFICIT’ towards attainment of noble gas configuration. Clearly, the skeletal numbers were being used just as numbers to explain something. But once more reflection is done and the numbers are understood better, it is discovered that these numbers are filled with deeper significance. They mean a lot. They enable us to immensely appreciate the tremendous insights of great scientists [15-16], namely Langmuir and Lewis, who had the visions of the concepts of 8 and 18 electron rules more than 90 years ago. Let us give a few examples (Ex-) as illustrations.

Ex-1a Wilkinson’s catalyst: RhCl(PPh₃)₃; K = 1[4.5]-0.5-3 = 1. The K value of 1 means that the complex has a shortage of 1 electron pair to achieve the 18 electron rule. Let us assign a 2-electron donor ligand the symbol L and a 1-electron donor ligand X and the central metal atom or skeletal element by M. In this way, we can represent the Wilkinson catalyst as MXL₃. If we donate one 2 electron donor ligand to the complex, it will achieve the required 18 electron rule. Thus, MXL₃ +L →MXL₄. The K value of MXL₄ is given by K = 1[4.5]-0.5-4 =0. This tells us that the complex is now saturated and has no electron pair deficit.

Ex-1b Vaska’s complex, IrCl(CO)L₂, L = PPh₃: K =1[4.5]-0.5-1-2 = 1. The cluster has a shortage of 1 pair of electrons. Hence, IrCl(CO)L2+ HCl→HIrCl₂(CO)L₂.

Ex-1c. BH₃; K = 1[2.5]-1.5 = 1. The borane has a shortage of 1 electron pair so as to attain the 8 electron rule. Hence, MX₃ + L →MX₃L. Therefore reactions such as BH₃ + CO→H₃B(CO) and BH₃ + NMe₃→H₃B(NMe₃) and BH₃ + H^― → BH₄^― are expected.

Ex-2a Mn₂(CO)₁₀; K = 2[5.5]-10 = 1. This complex also has a shortage of one electron pair in order to enable its skeletal elements to obey the 18-electron rule. Hence, M₂L₁₀ + 2H →2[MHL₅]. Alternatively, we could set a simple equation such as M₂L₁₀ + 2e^― →2[ML₅^―]

Ex-2b B₂H₆; K = 2[2.5]-3 = 2. This means the diborane needs 2 electron pairs for its skeletal atoms to obey the octet rule. For instance, B₂H₆ + 4H→ B₂H₁₀ →2[BH₅] = 2[BH₄^―].

Ex-3a Pd₃(CO)₃L₄ (L = 2 electron donor): Since the CO ligand is also a 2-electron donor, the complex can be written as M₃L₇ (M = Pd). Using the skeletal numbers, its K value is given by K = 3[4]-7 = 5. This complex needs 5 electron pairs; M₃L₇ + 5L → M₃L₁₂. This ‘heavy’ cluster decomposes into complexes expressed as, M₃L₁₂→3[ML₄] and each one of them obeys the 18 electron rule.

Ex-3b C₃H₆; K = 3[2]-3 = 3. Hence, C₃H₆+ 6H → C₃H₁₂→ 3[CH₄].

We can apply the concept of electron pair deficit to large clusters.

Ex-4a B₅H₉: K = 5[2.5]-4.5 = 8; B₅H₉+8x2H→ B₅H₂₅→5[BH₅] = 5[BH₄^―].

Ex-4b Os₅(CO)₁₅ (C): K = 5[5]-15-2 = 8; Os₅(CO)₁₅ (C)+ 8CO→ Os₅(CO)₂₃ (C)→ Os₅(CO)₂₅ →5[Os(CO)₅]

Ex-5a Rh₆(CO)₁₆: K = 6[4.5]-16 = 11; M₆L₁₆+11L→M₆L₂₇→6[ML_4.5] ≡ 6[ML₄X], ML₄X obeys the 18 electron rule.

Ex-5b B₆H₆^2―: K = 6[2.5]-3-1 = 11; B₆H₆^2―+ 11x2H ≡ B₆H₃₀→6[BH₅] ≡ 6[BH₄^―].

Ex-6a B₁₂H₁₂^2―: K = 12[2.5]-6-1 = 23; B₁₂H₁₂^2―+ 23x2H ≡ B₁₂H₆₀→12[BH₅] ≡ 12[BH₄^―].

Ex-6b Pd₁₃Ni₁₃(CO)₃₄^4―≡ M₂₆L₃₆: K = 26[4]-36 = 68. This is a deficit of 68 electron pairs. Hence, M₂₆L₃₆+ 68L →M₂₆L₁₀₄ ≡ 26[ML₄].

Ex-7 Pd₁₄₅L₉₀: K = 145[4]-90 = 490; Pd₁₄₅L₉₀+ 490L→Pd₁₄₅L₅₈₀ ≡ 145[PdL₄]

Due to the fact that the K values have a very important meaning, the skeletal elements K value Tables 1, 2 and 3 published earlier [12-14] have been reproduced to re-emphasize their new found meaning.

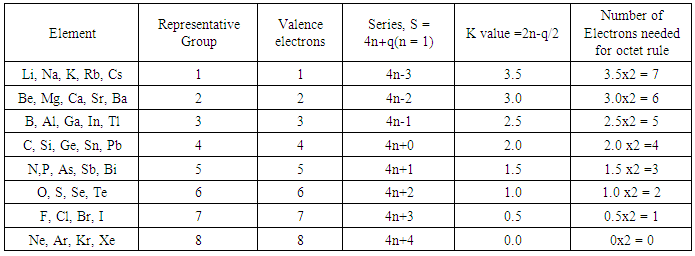Table 1. Skeletal Numbers of Main Group Elements and their Interpretation

2.1.2. The 18 Electron Rule (Table 2)

Just as the K value of the main group element has been interpreted as an indication of the deficit or shortage of the number of electron pairs needed to complete the 8-electron rule, the K value of a transition metal can be regarded as a deficit of the number of electrons pairs required by the element to complete the 18 electron rule. Starting with members of group 3, represented by Scandium, Sc, K = 7.5. This means that the scandium element or any one of its congeners (members of its family) requires 7.5x2 = 15 electrons for it to obey the 18 (3+15) electron rule. Titanium, Ti has a K value of 7.0. Therefore it requires 7x2 = 14 electrons in order for it to obey the 18 (14+4) electron rule. The same explanation applies to other transition metals of different groups as shown in Table 2.

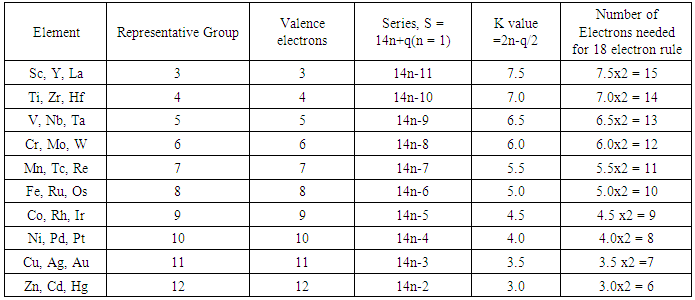Table 2. Skeletal Numbers of Transition Metals and their Interpretation

2.1.3. The Ligands

Whereas the skeletal elements in Tables 1 and 2 require electron pairs so as to obey the 8 or 18 electron rules, the ligands only act as suppliers of the needed electrons to enable the respective skeletal elements obey either 8 (main group element) or 18(transition element) electron rule. They are regarded as the electron donors. Hence their K values are rightly assigned the negative values. By the addition of a ligand to a skeletal element or cluster, the number of skeletal linkages are reduced. IN THIS WAY, THE LIGANDS CAN BE REGARDED AS REDUCING AGENTS OF SKELETAL LINKAGES (OR NUMBERS). Hence, the K values of ligands reflect the number of electron pairs they contribute towards reducing the number of skeletal linkages of a fragment or cluster being considered. The skeletal numbers of a few selected ligands are shown in Table 3.

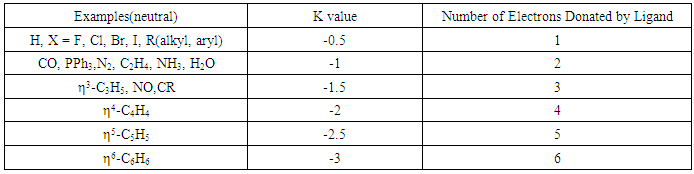Table 3. The Skeletal Numbers of Ligands and their Interpretation

2.2. Nuclearity Index and Cluster Trees and Branches (Series)

The term ‘Nuclearity’ is widely used in cluster chemistry [17]. Some clusters are referred to as being of low or high nuclearity. It has been found that in the application of the series method, it will be better to specify the number of skeletal elements being considered in a given cluster. In this regard, if a cluster has got one skeletal element being considered, it is proposed we give it a symbol N-1 and for the two skeletal elements N-2 and three N-3 and so on. We could as well add on the word ‘index’, for example, N-5 will refer to a cluster of nuclearity index 5 meaning that the cluster has 5 defined skeletal elements. In this regard, CH₄, C₂H₄, C₃H₄, can be considered as having nuclearity indices N-1, N-2, and N-3 respectively in the same way as Fe(CO)₅, Fe₂(CO)₉ and Fe₃(CO)₁₂. Applying the isolobal relationship of series, 4n+q⥈14n+q, the isolobal equivalent species for the main group elements and transition metals have been grouped together (Table 4). Each set of isolobal elements of the same K(n) value for selected fragments have been grouped together. They can be considered as members of the same family (isolobal family analogues). This method is based on the categorizing together of groups of fragments, molecules and clusters with the same nuclearity index and the same electron pair deficit.

Looking at Table 2, group 3 transition metals have the highest K value of 7.5. If we take M⁺ (K= 8) ion for group 3 transition elements, for one skeletal element or a cluster of nuclearity index N-1, then its K value is 8. This means the ion has a shortage of 8 electron pairs to so as to attain the 18 electron rule, that is, the M⁺ ion has 2 valence electrons. We can regard this as being the highest K value for one skeletal element cluster element N-1 can have. This is because the K values of neutral elements range from K = 7.5 to K =0 for transition and main group elements as can be seen in Tables 1 and 2. Hence, the K(n) values will then range from K(n) = 8(1) to K(n) = 0(1). These values are shown in Table 4. The K values of clusters and fragments are easily calculated using the skeletal numbers given in Tables 1 and 2. For instance, CH₄, K = 1[2]-4(0.5) = 0,K(n) = 0(1), Fe(CO)₅, K = 1[5]-5(1) = 0, K(n) = 0(1), RhCl(PPh₃)₃, K =1[4.5]-0.5-3(1) = 1, K(n) = 1(1), NbF₇^2―; 1[6.5]-7(0.5)-1 = 6.5-3.5-1 = 2; K(n) = 2(1). The fragments with K =0 values have zero electron pair deficit and obey the 8 or 18 electron rule, while those with K= 1 or 2 have one or two electron pair shortfalls. Since these fragments are grouped under different K(n) values, these may be considered to form branches of the N-1 tree. It is quite clear from Table 4 that the chemical species that obey the octet(8) rule or the 18 electron rule are just members of the series S = 4n+4 and a branch of N-1 tree(shown below) with K(n) value of 0(1). Since these species are linked to the noble gas configurations, they are generally very stable. The complexes with K(n) = 1(1), have a shortage of 1 electron pair and belong to series branch S = 4n+2. In this paper the cluster trees N-1, N-3 and N-6 will be used as illustrations of one of the ways of categorizing clusters. The advantage of using these types of trees is that ∆K = ±1 and ∆n = 0. It is much easier to monitor the movement of changes on K value of one unit when the number of skeletal elements remains constant. The changes on K value just depend upon the ELECTRON DENSITY. When the electron density decreases by removing ligands the value of K increases and when the number of ligands increases K decreases.

2.2.1. The N-1 Series and Tree

As explained earlier, the K values can be regarded as an indication of electron pair deficit in order for the fragment in question to attain either 8 or 18 electron rule. A complex such as Fe(CO)₅ with K(n) = 0(1), means that it has a ZERO electron pair deficit. That is, it obeys the 18 electron rule. On the other hand, the fragment, Fe(CO)₄, K(n) = 1(1) has a K value of 1. This means that it has a deficit of one electron pair of electrons to reach 18 electrons and hence the fragment has a valence electron content of 16. Also the 14n/4n series developed can be utilized to generate the valence electrons of the fragments or clusters. We can regard the K(n) parameter as a measure of the number of electron pair deficits for the corresponding number of skeletal elements. Let us take simple examples for illustrations. The S = 4n+4 series becomes V = 14n+4 for the purpose of calculating valence electrons (meaning those of the central metal atom plus the electrons donated by the ligands). In case of N-1, n = 1, the valence electrons, V = 14n+4 = 14(1)+4 = 18 and K = 2n-2 = 2(1)-2 = 0 and hence K(n) = 0(1). Thus, the N-1 transition metal clusters which belong to S = 14n+4 series or shortened to 4n+4 do obey the 18 electron rule. These include, among others, the iron-based complexes such as Fe(CO)₅, Fe(CO)₄^2―, Fe(CO)₃L₂, HFe(CO)₄^―, H₂Fe(CO)₄, (Cp)Fe(CO)₂^―, Fe(CO)₆²⁺, (Cp)Fe(CO)₂Cl, Fe(CO)₃(η⁴-C₄H₆) and ( η⁵-C₅H₅)₂Fe. Each of these complexes has a content of 18 electrons as in the case of Fe(CO)₅, V = 1[8]+5x2 = 18. As we are aware, the 18 electron rule members are comparatively more stable. Let us consider the series S = 4n+2. The valence electrons for the clusters with a transition metal skeletal element, V= 14n+2 = 14(1)+2 = 16. The valence electrons for the complex PtCl₄^2―, V = 1[10]+4+2 = 16; RhCl(PPh₃)₃, V = 1[9]+1+3x2 = 16. Other members of S = 4n+2 include HIr(CO)(PPh₃)₂, HPtCl(PPh₃)₂, (C₂H₄)PdCl₂, Fe(CN)₆^2― and (Cp)₂TiCl₂. We can also derive the series of other N-1 complexes which do not obey the 18 electron rule. For instance, Fe(CN)₆^3―; K = 1[5]-6(0.5)-3(0.5) = 5-3-1.5 = 0.5, K(n) = 0.5(1), S = 4n+3, V = 14n+3 = 14(1)+3 = 17. This agrees with 1[8]+6+3 = 17 value obtained directly from the cluster formula. Since a positive K value is an indication of electron pair deficit, a K value of 0.5 implies a deficit of 1 electron which agrees with the valence electron figure of 17. Take the complex, Cu(NH₃)₆²⁺; K = 1[3.5]+6(-1)+1=-1.5. The cluster has e negative K value of -1.5, it implies that it has an excess of one and half electron pairs beyond the 18 or 8 electron rule. In this case of the copper complex, K(n) = -1.5(1), S = 4n+7, and V = 14n+7 = 14(1)+7 = 21. This also agrees with the calculation from the formula of the copper complex, V = 1[11]+6(2)-2 = 11+10 = 21. Clearly, the complex exceeds the 18 electron rule by 3 electrons. The above examples do illustrate that all N-1 complexes can be categorized into series. It is proposed that we regard the series, S = 4n+7, 4n+6, 4n+5, 4n+4, 4n+3, 4n+2,4n+1, 4n+0, 4n-1, 4n-2, 4n-3, 4n-4 and so on as BRANCHES OF N-1 CLUSTER TREE. In most cases of the series we encounter S = 4n+q where q has values comprising of even numbers. It must be recognized that in some cases q takes on odd numbers. Although the transition metal fragments and clusters of N-1 have been discussed, the same approach can be applied to the main group elements. The categorization puts together fragments and clusters which are isolobal and hence belong to the same series with the same K values. It is important to emphasize the important isolobal series relationship S = 14n+q⥈S = 4n+q which relates the transition metals clusters and fragments with main group clusters and fragments. This relationship was encountered in earlier work [18]. Selected complexes, fragments and series of N-1 tree are shown Table 4 and the corresponding tree is shown in N-1.

2.2.2. Application of K Parameter to Interpret a Catalytic Cycle

Mono-skeletal clusters (N-1) are widely utilized in catalysis [19-20]. The most common catalysts utilized have the K value switching from 1 to 0 or vice-versa. A good example is hydroformylation [19]. The simplified steps of the catalysis are shown in the Figure 1. In the first step (S-1) the cobalt complex HCo(CO)₄ has K =0(saturated). It loses a CO ligand to increase the K value to 1(S-2) creating a deficit of 1 electron pair. A ligand in the form of C₂H₄ comes in and donates one electron pair to erase the deficit and the new complex at S-3 becomes saturated, K = 0. The reaction of coordinated H and C₂H₄ ligands generates an alkyl ligand, -CH₂CH₃(Et) at S-4. Due to that ligand rearrangement, the K value increases back to 1. The creation of a shortage of one electron pair at S-4 allows the entrance of a CO ligand. The process goes on until the product RCHO (R = Et) is produced at S-7 and the active fragment HCo(CO)₃ is regenerated. The use of K value in the interpretation of the catalytic cycle eases the capturing of the electron counting process and the mechanistic steps. It is important to note that in calculating the K value, the skeletal elements and the ligands are taken as neutral species. In this regard, H•, R•, X•. R-C(O)• are formally considered to be single electron donors with a K value = -0.5.

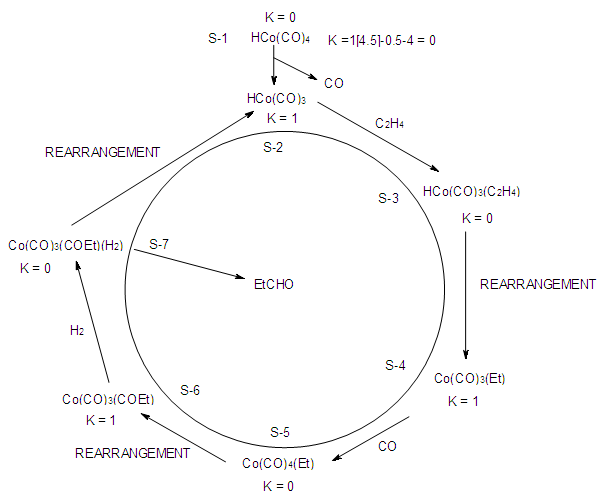Figure 1. An Illustration of Application of K parameter in the Interpretation of a Catalytic Cycle

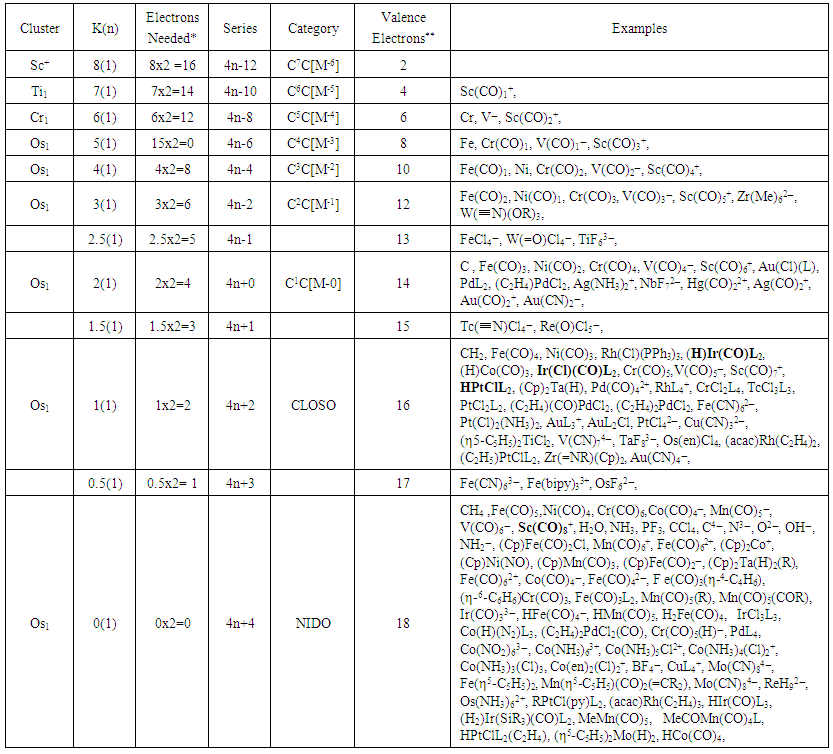Table 4. The Skeletal Numbers of N-1 Tree and their Interpretation

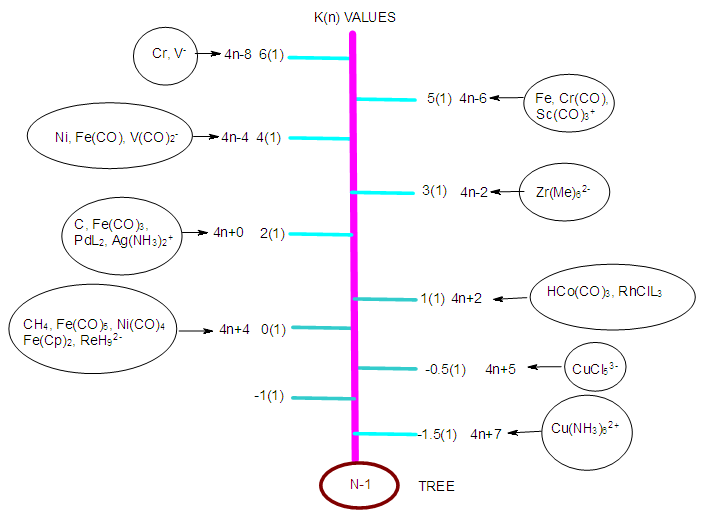N-1 Tree

2.2.3. N-3 Tree

The N-3 tree refers to clusters with 3 defined skeletal elements either from the main group elements or transition metals or both. The K values of N-3 skeletal elements represent the deficit number of electron pairs required to enable the respective elements achieve the noble gas configuration either 8 or 18 electron rule. If we take osmium, Os (K =5) as a reference element, then Os₃ (K = 3x5 =15). This means that the three skeletal atoms require 15 pairs of electrons in total for each of them to attain an 18 electron configuration. Thus, the starting K (n) value will be symbolized as 15(3). As we have learnt from previous work [21], addition of a two (2) electron donor ligand such as CO or PPh₃ to the naked skeletal cluster Os₃ will decrease (REDUCE) the original K value of 15 by 1. Successive addition of the ligand stepwise will decrease the K value by one until K = 2 for an N-3 skeletal cluster. In previous work [21], it was found that a meaningful K value for a cluster of nuclearity index n, is k =n-1. This means for a cluster of n =1, the last meaningful K value will be K = n-1 = 1-1 = 0. Thus, the range of K(n) values for Os(1), will be [5(1), 4(1), 3(1), 2(1) and 0(1)]. For n = 2, taking Os₂ as a reference, the last K value will be K = n-1 = 2-1 =1, with corresponding K(n) range of [10(2), 9(2), 8(2), 7(2), 6(2), 5(2), 4(2), 3(2), 2(2) and 1(2)]. Also for n =3, the last K value will be K = 2, n = 4, K = 3, n = 5, K= 4 and so on. The carbon-based clusters such as C₂H₆, C₂H₄, C₂H₂, and C₂ with respective K values of 1, 2, 3 and 4 can be symbolized as 1(2), 2(2), 3(2) and 4(2) respectively. In the case of N-3, again taking Os₃ as a reference, the range of K(n) values will be [15(3), 14(3), 13(3), 12(3), 11(3), 10(3), 9(3), 8(3), 7(3), 6(3), 5(3), 4(3), 3(3) and 2(3). This range gives us the last K value for n = 3 as K = 2. The hypothetical scheme for skeletal clusters of nuclearity index 3 is given in Table 5 and N-3 tree. There are good examples of clusters that belong to N-3 tree. These include, K(n) = 2(3); S = 4n+8, Re₃H₂(CO)₁₃^―, TeCr₂(CO)₁₀^2―, C₃H₈; K(n) = 3(3), S = 4n+6, Os₃(CO)₁₂, Re₃H₂(CO)₁₂^―, C₃H₆; K(n) = 4(3), S = 4n+4, Os₃H₂(CO)₁₀, Mo₂(Cp)₂(CO)₄Fe(CO)₄; K(n) = 5(3), S = 4n+2, C₃H₂, Mo₂(Cp)₂(CO)₄PtL₂.

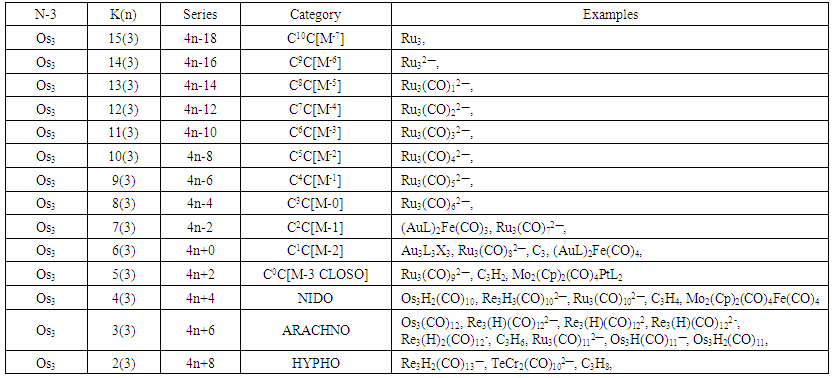Table 5. The Skeletal Numbers of N-3 Tree and their Interpretation

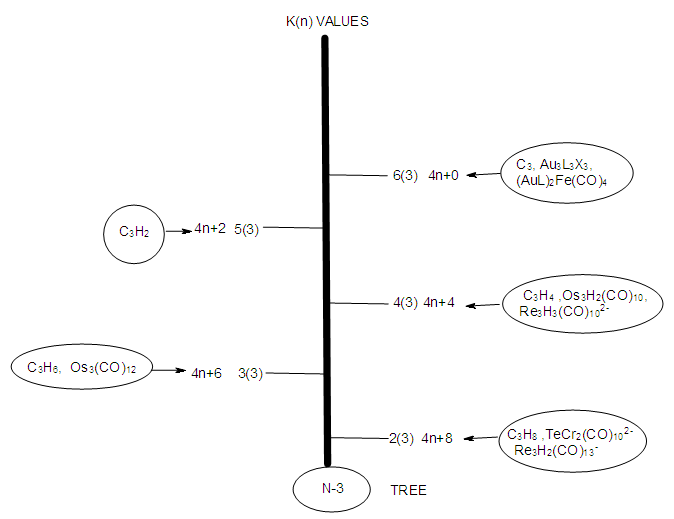N-3 Tree

2.2.4. N-6 Tree

The N-6 cluster tree comprises of clusters with 6 skeletal elements. Again, it is important to emphasize the fact that the K(n) parameter represents the number of electron pair deficit (K) required by the skeletal atoms(n) in order to meet the requirements for attaining the noble gas configuration. The list of N-6 clusters is huge. A few examples will be listed here. These include, K(n) = 5(6), S = 4n+14, C₆H₁₄, K(n) = 6(6), S = 4n+12, C₆H₁₂,Re₆H₅(CO)₂₄^―, K(n) = 7(6) = 4n+10, C₆H₁₀, K(n) =4n+8, C₆H₈, K(n) = 9(6) = C₆H₆, Os₆L₄(CO)₁₇,K(n) = 10(6), S = 4n+4, B₆H₁₀, (Cp*Ru)₂B₄H₁₀, K(n) = 11(6), S = 4n+2, Os₆(CO)₁₈^2―, Rh₆(CO)₁₆, B₆H₆^2―, K(n) = 12(6), S = 4n+0, Os₆(CO)₁₈, Os₄H₂(CO)₁₂(AuL)₂, K(n) = 4n-4, Au₆L₈²⁺, and K(n) = 15(6), S = 4n-6, (AuL)₅Mo(CO)₄⁺. A collection of K(n) cluster series associated with N-6 cluster tree are given in Table 6 and the N-6 tree. Just to emphasize the concept of an electron pair deficit, let us consider a benzene cluster, C₆H₆(K =9). Its K(n) symbol is 9(6). The K(n) symbol informs us that the 6 benzene skeletal atoms require 9 electron pairs to enable each one of them to obey the octet rule. If we assume that those 9 electron pairs needed are all H atoms, then if we add them to the benzene cluster, it will decompose into 6 molecules each of which will obey the 8 electron rule. That is, C₆H₆ +18H→ C₆H₂₄ = 6[CH₄] and we know that CH₄ obeys the 8 electron rule. The fragments and clusters are arranged according to their K(n) values.

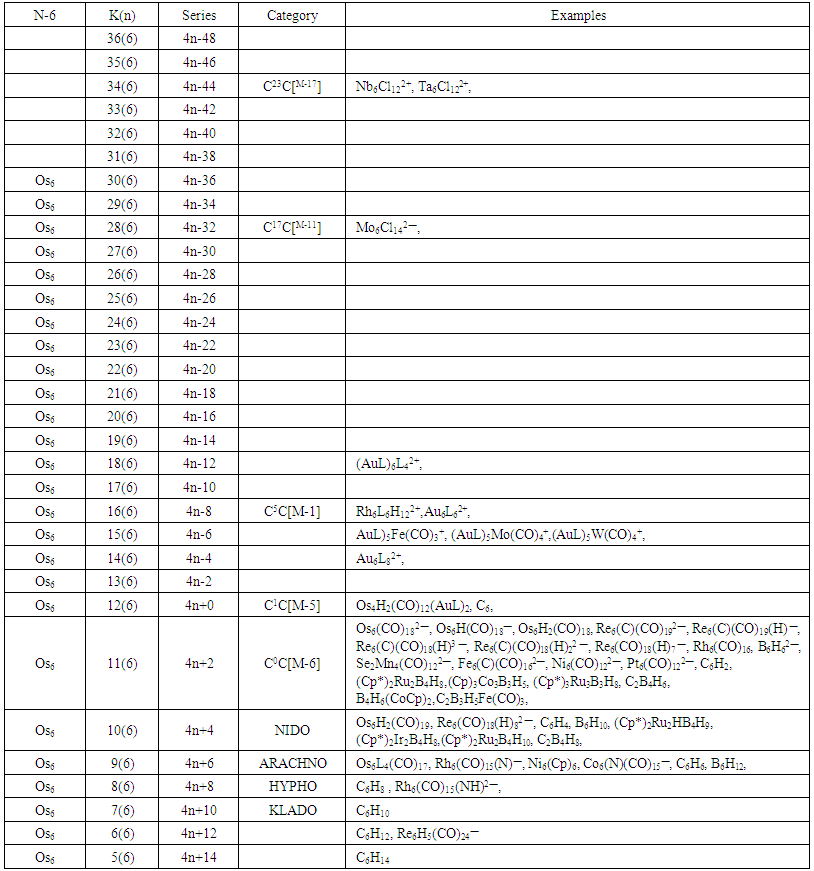Table 6. Skeletal Numbers of N-6 Tree and their Interpretation

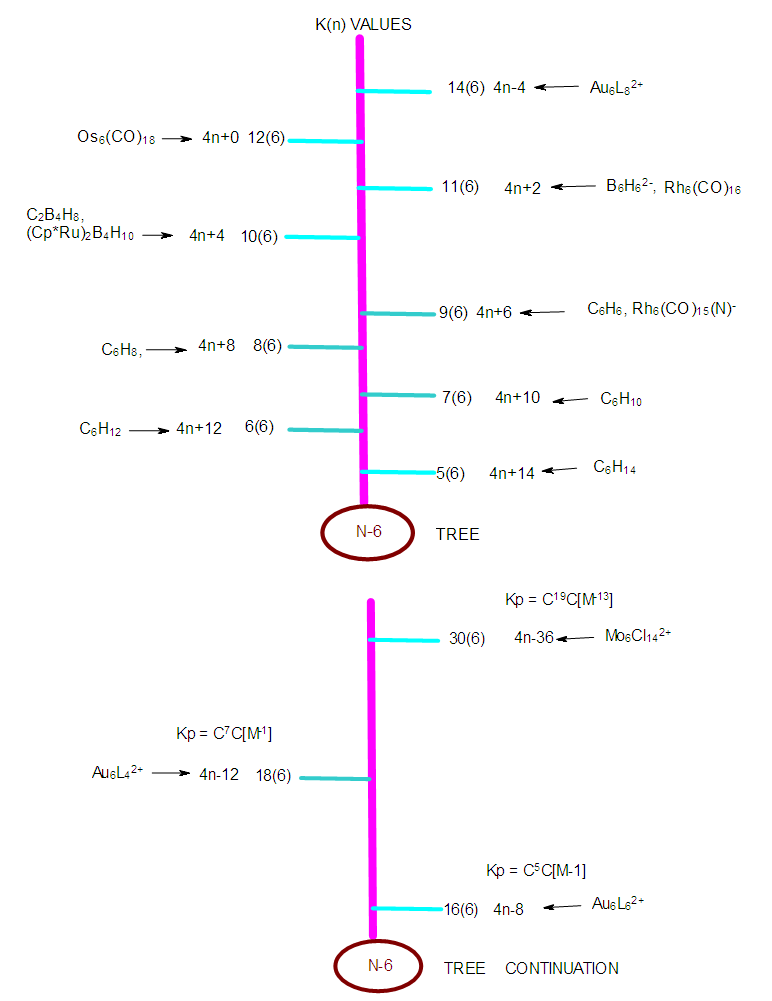N-6 Tree

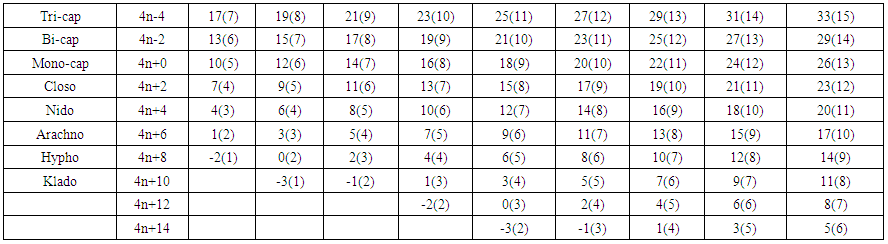
2.2.5. The Cluster Tree Map

The K(n) values can be portrayed in tabular form. A selected portion of the K(n) Table is given in Table 7. The table can be extended as required. The cluster trees N-1, N-3 and N-6 are indicated as shaded diagonals from left to right. The table can readily be constructed by using rows (ORDINARY SERIES, ∆K = ±2, ∆n = ±1) starting from a preferred K(n) point or using the columns (SPECIAL SERIES, ∆K = ±3, ∆n = ±1). The table can be extended as desired. Clearly, this table is of tremendous importance as it gives the mapped K(n) values of thousands of clusters. More than that it gives the sets of skeletal numbers with their corresponding shortage of electron pairs needed for the skeletal elements to obey the 8 or 18 electron rules. Consider the following clusters: Ru₅(CO)₁₆, K(n) = 9(5); Ru₆(CO)₁₈, K(n) = 12(6); Ru₇(CO)₂₀, K(n) = 15(7); Ru₈(CO)₂₂, K(n) = 18(8); Ru₉(CO)₂₄, K(n) = 21(9); Ru₁₀(CO)₂₆, K(n) = 24(10); Ru₁₁(CO)₂₈, K(n) = 27(11) and Ru₁₂(CO)₃₀, K(n) = 30(12). All these clusters form a vertical (column) in which 9(5), trigonal bipyramid cluster is the nucleus and the rest are capping series. The series of K(n) to observe are 9(5)→12(6)→15(7)→18(8)→21(9) →24(10)→27(11)→30(12). They are all capping series: Kp = C⁰C[M-5]→ C¹C[M-5] C²C[M-5] → C³C[M-5] → C⁴C[M-5] → C⁵C[M-5] → C⁶C[M-5] → C⁷C[M-5]. This is the trigonal bipyramid capping family. These capping clusters are indicated in blue along [M-5] column. Table 7 is so important that if we reflect more, it is discovered that hidden in the numbers in the table are the 18 and 8 electron rules. Take the example of B₆H₆^2― [K =6(2.5]-3-1 = 11] cluster. Its K(n) symbol is 11(6). This value can be located in Table 7 and has been highlighted. This symbol means that B₆H₆^2― cluster needs 11 electron pairs in order for each of all the 6 boron skeletal elements to fulfill the 8 electron rule. Hence, B₆H₆^2― + 11x2 H →B₆H₂₈^2― = B₆H₃₀. The B₆H₃₀ cluster decomposes into 6[BH₅]. The BH₅ fragment can be regarded as equivalent to the well-known ion complex BH₄^― which obeys the octet rule. If we take a transition metal cluster such as Os₆(CO)₁₈^2―, its K value can be calculated as 6[5] -18-1 = 11. The K(n) parameter associated with it is also 11(6) as in the case of the borane cluster B₆H₆^2―. Therefore according to the series method and Table 7, it requires 11 electron pairs in order for all its skeletal elements to attain the 18 electron rule. That is, Os₆(CO)₁₈^2―+ 11CO →Os₆(CO)₂₉^2― = Os₆(CO)₃₀. This heavy complex is equivalent to 6[Os(CO)₅]. The Os(CO)₅ complex obeys the 18 electron rule. The cluster [22] Pd₂₃(CO)₂₀L₁₀(L = PEt₃) has a K value given by K =23[4]-20-10 = 62, K(n) = 62(23). This informs us that the cluster has a deficit of 62 electron pairs in order for all its skeletal elements (23 palladium atoms) to obey the 18 electron rule. Therefore, if we give the cluster 62 electron pairs for instance in terms of CO ligands, the entire cluster will obey the 18 electron rule. Hence, Pd₂₃L₃₀+62L→Pd₂₃L₉₂ (L = CO or PEt₃ or any 2 electron donor ligand). The heavy cluster Pd₂₃L₉₂ is equivalent to 23[PdL₄]. The complex PdL₄ obeys the 18 electron rule. Also from Table 7, we can read off the series of the cluster Pd₂₃(CO)₂₀L₁₀, S = 4n-32, Kp = C¹⁷C[M-6]. This means the cluster has 6 skeletal elements which adopted an octahedral geometry in the nucleus which is surrounded by 17 remaining skeletal palladium atoms. Another cluster, Pd₂₃(CO)₂₀L₈(L = PEt₃): K =23[4]-20-8 = 64, K(n) = 64(23). It has been stated that ligands can be considered as reducing agents of skeletal linkages. Since Pd₂₃(CO)₂₀L₁₀ has two more two electron donor ligands than Pd₂₃(CO)₂₀L₈, the former will have 2 skeletal linkages less than the latter. This is what is obtained from the simple calculation of the K values. The K value of 64 means the cluster Pd₂₃(CO)₂₀L₈, will need 64 electron pairs so as to achieve the 18 electron rule. Furthermore, from Table 7, the cluster belongs to S = 4n-36, Kp = C¹⁹C[M-4]. This capping symbol implies that by having 2 ligands less, the 23 skeletal elements arrange themselves in such way that the cluster adopts a tetrahedral nucleus, [M-4] which is surrounded by capping 19 remaining skeletal palladium atoms. The capping concept has been discussed in earlier work except that the capping symbol Kp has now been used instead of Cp so as to distinguish it from that used for the cyclopentadienyl fragment in previous work [23]. The cluster map concept was recently introduced and skeletal numbers tabulated [14]. However, those skeletal numbers derived from the series method were being utilized to categorize and predict the geometrical shapes of clusters without deep comprehension of what they really meant until relatively more recently. It is being reproduced so as to re-emphasize THE VITAL INFORMATION IT IS LOADED WITH. That is, hidden under those K(n) numbers are the two HISTORICAL IMPORTANT RULES, THE 18 AND 8 ELECTRON RULES. Let me clarify this point further by a few illustrative examples. Let us consider two clusters of the N-13 tree. These are Au₁₃L₁₀Cl₂³⁺ (L = PPh₃) [24]: K =13[3.5]-10-1+1.5 = 36, K(n) =36(13), S = 4n-20(see Table 7), Kp = C¹¹C[M-2], Rh₁₃(CO)₂₄(H)^4―: [25] K = 13[4.5]-24-0.5-2 = 32, K(n) = 32(13), S = 4n-12, Kp = C⁷C[M-6] and C₁₃H₂₈: K = 13(2)-14 = 12(13), S =4n+28. The K(n) changes involved are 36(13)→32(13)→12(13). In 36(13) case, there are two skeletal elements in the nucleus surrounded by 11 capping skeletal elements. The skeletal elements of the cluster adopt more or less an icosahedral symmetry. According to the series, the [M-2] symbol means there are two skeletal elements which obey the closo series S = 4n+2 and K = 2n-1 = 2(2)-1 = 3. This means the two elements in the nucleus are linked by a triple bond Au≡Au(K = 3) and each of the 11 capping skeletal atoms is associated with 3 linkages giving a net of 11x3 = 33 linkages. However, the overall cluster belongs to the series S = 4n-20 and the grand total of the linkages is 3+33 = 36. These 36 linkages we now know represent the number of electron pairs needed to dismantle the entire cluster into 13 mono-skeletal complexes which individually obey the 18 electron rule. We can set up a simple equation for this process: Au₁₃L₁₀Cl₂³⁺≡ Au₁₃L₁₁³⁺→Au₁₃L₁₁³⁺ + 36L ≡ Au₁₃L₄₇³⁺ ≡ Au₁₃L_45.5 ≡ 13[AuL_3.5]. As can clearly be seen the complex AuL_3.5 obeys the 18 electron rule, that is, 11+3.5x2 = 18. What happens then when the cluster reaches K(n) = 32(13)? From 36(13) to 32(13), there is a decrease of 4 skeletal linkages. For each decrease by K = 1, the capping elements also decrease by 1 which goes to create an increase in the number of skeletal elements in the nucleus. This means from 36(13) to 32(13), the number of skeletal atoms in the nucleus increases from 2 to 6.

The result is the creation of an octahedral nuclear cluster surrounded by 7 capping skeletal elements. The octahedral nucleus also obeys the closo series S = 4n+2 and K = 2n-1 = 2(6)-1 = 11. Since there are 7 capping elements, then the capping linkages will be 7x3 = 21. However the overall total linkages will be 11+21 = 32. When the cluster reaches 12(13) from 36(13), a total 36-12 = 24 linkages have been removed. The K(n) = 12(13) gives the saturated hydrocarbon chain before. With further decrease in K value below K ≤12, the cluster begins to fragment [26].

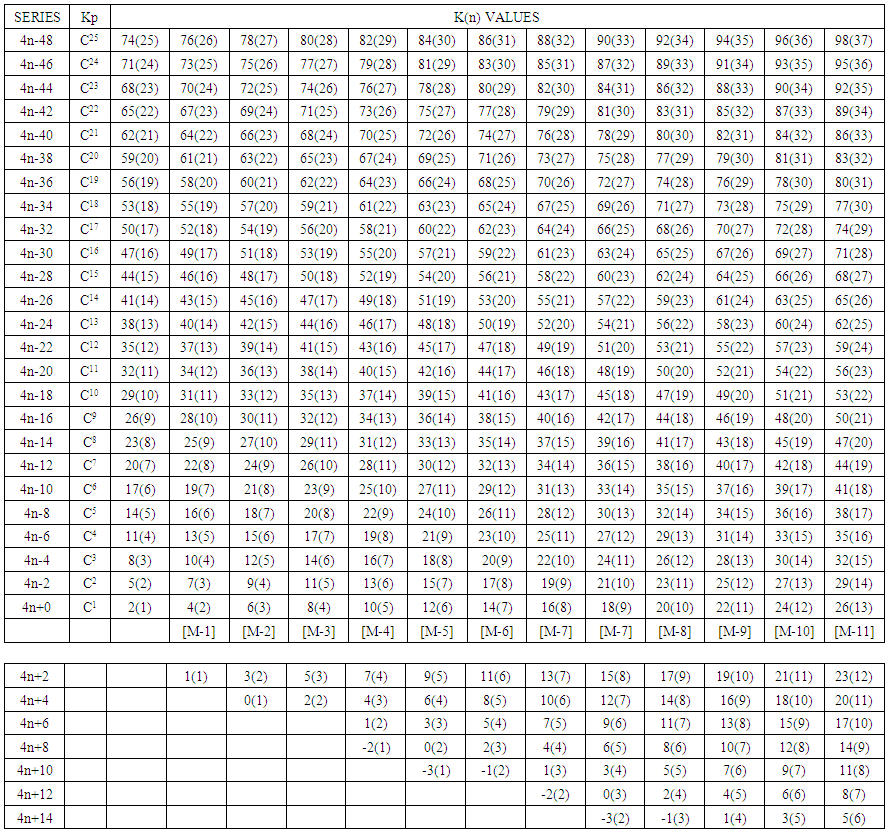Table 7. A Map of Selected Nuclear Trees Showing the K(n) Values

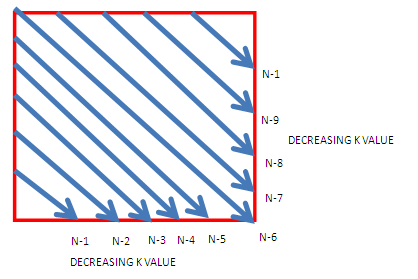Figure 2. Sketch Indicating the Direction of Nuclearity Trees

2.2.6. Special Types of Cluster Series

There are three types of cluster series, normally encountered. These will be illustrated by a few examples. Let us take the clusters, Os₂(CO)₈^2―, K =2[5]-8-1 = 1; K(n) = 1(2). We know that K = 2n-q/2 = 1 = 2(2)-q/2. Hence, q/2 =4-1 = 3 and q = 6. Therefore S = 4n+q = 4n+6. This corresponds to ARACHNO series. Similarly, the cluster, Os₃(CO)₁₂, K = 3[5]-12 =3; S = 4n+6, also Os₄(CO)₁₅, K = 4[5]-15 =5; S = 4n+6, and Os₅(CO)₁₈, K =5[5]-18= 7, S =4n+6. These clusters form series with ∆K = 2(∆n = 1). From one cluster to the next, there is a difference of Os(CO)₃ fragment. The fragment belongs to S = 4n+0 series and since q = 0, there is no change in the type of series when the fragment is added successively. Let us look at another type of cluster series, Os₃(CO)₁₂, K = 3; K(n) = 3(3), S = 4n+6( ARACHNO), Os₄(CO)₁₄, K = 4[5]-14 = 6;K(n) = 6(4), S = S = 4n+4(NIDO), Os₅(CO)₁₆, K = 9,K(n) = 9(5), S = 4n+2(CLOSO), and Os₆(CO)₁₈, K = 12, K(n) = 12(6), S = 4n+0(mono-capped). This type of series are characterized by ∆K =3(∆n = 1). This is RUDOLPH type of series [27] used to categorize clusters such as boranes, carboranes and carbonyls and are also consistent with Wade-Mingos rules that have widely been used [2-3]. Let us look at another third special type of cluster series, Os₅(CO)₁₉, K = 5[5]-19 = 6; K(n) = 6(5), S = 4n+8; Os₅(CO)₁₈, K = 7, K(n) = 7(5); Os₅(CO)₁₆(H)₂, K = 8; and Os₅(CO)₁₆, K = 9, K(n) = 9(5), S = 4n+2(CLOSO). The characteristic of this type of series, is ∆K = 1(∆n = 0). THIS SPECIAL TYPE OF SERIES IS THE BASIS OF THE NUCLEARITY CLUSTER TREES.

2.2.7. Ordinary Series, S = 4n+q

In previous work the q variable of the series 4n+q was regarded as a DETERMINANT of the type of series. For instance, if q = 2, the series are CLOSO type, q = 4, NIDO, and q = 8, HYPHO, and finally, q = 10, KLADO. When q = 0, the series are MONO-CAPPED, q = -2, BICAPPED, q = -4, TRICAPPED, q = -6, TETRACAPPED, and so on.

2.2.8. The Nuclearity Trees and Series

As can be discerned from Table 8, the nuclearity trees correspond to the special series (∆K = ±1, ∆n = 0). With this type of series, there is only one variable, that is, ∆k = +1 when the ELECTRON DENSITY on the skeletal elements is decreasing by stripping off ligands, or ∆K = -1 when the electron density of the fixed number of skeletal elements is kept constant. With the other two special series both K and n do change as we move from one K(n) value to the next. The types of series are illustrated in Figure 3. The K(n) values of clusters can readily be calculated. The categorization of a cluster can be derived from the K(n) or obtained directly from the Nulearity Map in Table 7. However, some huge clusters may be outside the nuclearity map in which case the categorization may be done from the K(n) parameter itself. Let us consider this huge cluster with nuclearity index N-44, Ni₃₈Pt₆(CO)₄₈^6―, K(n) = 83(30), S = 4n-74, Kp = C³⁸C[M-6]. The series indicate that it has an octahedral nucleus surrounded by 38 capping atoms. Amazingly, this was found to be the case with the 6 platinum skeletal atoms residing in the nucleus [28].

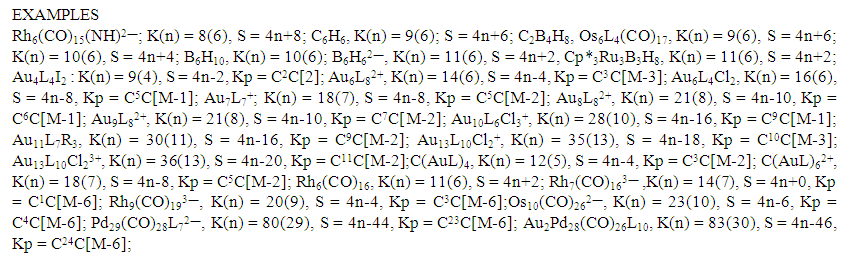Scheme 1. Selected examples of clusters categorized Using the Cluster Nuclearity Map

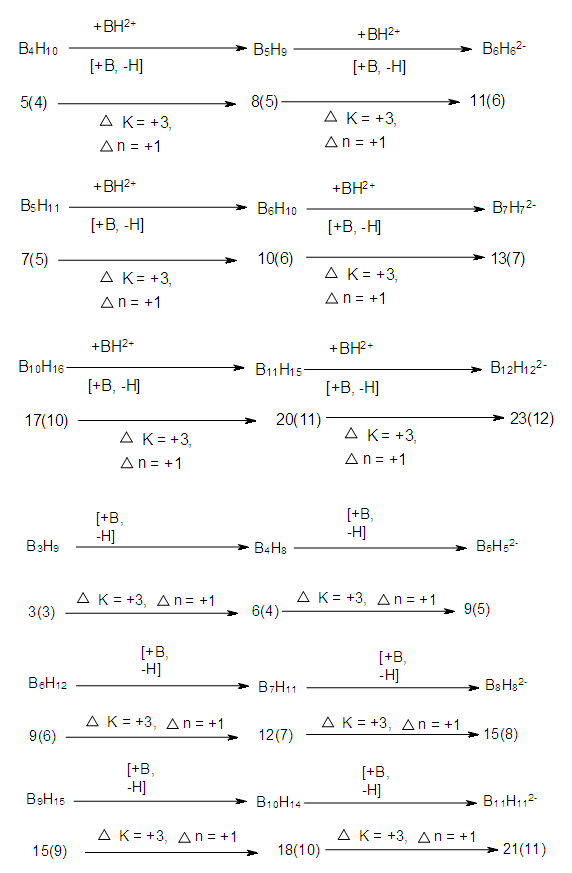
2.2.9. Wade Mingos Rudolph System

[BH]²⁺, K = 1[2.5]-0.5+1 = 3, K(n) = 3(1), K = 2n-q/2 = 3= 2(1)-q/2, q/2 = 2-3 = -1. Hence, q = -2 and S = 4n+q = 4n-2. This means the fragment belongs to the capping series S = 4n-2. Its valence electron content can also be obtained by using the same formula V = 4n-2 = 4(1)-2 = 2 in agreement with the valence electron content obtained from the fragment directly, V = [3+1]-2 = 2. If we examine carefully the set of numbers, 5(4)→8(5)→11(6); 7(5)→10(6)→13(7) and 17(10)→20(11)→23(12), they are all found in the WADE-MINGOS-RUDOLPH numerical vertical system above. Let us look at other sets of numbers. These are 3(3)→6(4)→9(5); 9(6)→12(7)→15(8) and 15(9)→18(10)→21(11). Also these sets of numbers can clearly be seen in the Wade-Mingos-Rudolph numerical system in Table 8.

Table 8. Section of the Nuclear Tree Map where mostly Main Group Elements are Found

Scheme 2. Selected Wade Mingos Rudolph Correlation Clusters

Isolobal fragments:

K = 0; CH₄(S = 4n+4)⥈ Fe(CO)₅(S =14n+4)⥈ CH₃^―(4n+4)⥈ NH₃(4n+4)⥈ Mn(CO)₅^―(14n+4). Analogues can be added, e.g. CH₄, there are SiH₄, GeH₄, SnH₄.

K = 0.5; CH₃(S = 4n+3)⥈ BH₃^―(4n+3) ⥈Mn(CO)₅(14n+3)⥈ Fe(CO)₅⁺(14n+3)⥈ Mo(CO)₅^―(14n+3)⥈ Fe(CO)₂Cp(14n+3)⥈ Mo(CO)₃Cp(14n+3)⥈ Co(CO)₄(14n+3).

K = 1; CH₂(S =4n+2)⥈ CH₃⁺(4n+2)⥈ Fe(CO)₄ (14n+2)⥈ ⥈ CH₃⁺(4n+2)⥈ Mn(CO)₅⁺(14n+2)⥈ BH₃(4n+2)⥈ Cr(CO)₅(14n+2)⥈ SiH(4n+2)₂⥈ Ru(CO)₄(14n+2)⥈ Os(CO)₄(14n+2)⥈ Re(CO)₂Cp(14n+2)⥈ TaMe(Cp)₂(14n+2)

K = 1.5; CH(4n+1) ⥈ Co(CO)₃(14n+1)⥈ NiCp(14n+1)⥈ Rh(η⁶-C₆H₆) (14n+1)⥈ Mn(CO)₄(14n+1)⥈ Mo(CO)₂Cp(14n+1)⥈ CH₂⁺(4n+1).

Table 9. Skeletal Numbers of Isolobal Fragments and their Interpretation

2.2.10. Isolobal Chemical Fragments and the Meaning of Their K Values

The concept of isolobal fragments may be analyzed in terms of electron pair deficit. For instance, for [Mn(CO)₅], K = 1[5.5]-5 = 0.5. This means the fragment of a mono-skeletal element, [Mn] has a deficit of 0.5 electron pairs(1e) so as to obey the 18 electron rule. It also implies that the complex ion, [Mn(CO)₅^―] or [Mn(CO)₅X], complexes where X is a single electron donor can be produced. This also applies to the [CH₃] fragment. Hence, Mn(CO)₅⥈CH₃. The fragment [NiCp] has a K value of 1.5. This means it has a deficit of 1.5 electron pairs to achieve the 18 electron rule requirement. Therefore, it has 15 electrons and requires only 3. This can be fulfilled by adding a H atom and a CO ligand to form the complex Ni(Cp)(H)(CO). Also the [CH] fragment has a K value of 1.5. One of the ways it can do this is by receiving 3H atoms, that is, CH +3H →CH₄. It can also combine with another CH fragment to form C₂H₂ molecule. It requires 3 electrons so as to achieve the 8 electron configuration. It can do this by accepting 3 more electrons. Since [CH] fragment has the same K value as [NiCp], the two are isolobal, [NiCp]⥈[CH]. The K value of an isolobal fragment can readily be calculated using the skeletal numbers. The K values of selected fragments and their derivation are shown in Table 4. The meaning of the K value can be interpreted in the same way as the in the case of the main group elements (Table 1) or transition metal elements (Table 2). The K value simply means the number of electron pairs needed for a fragment to obey the 8 electron rule (main group element) or the 18 (transition metal element) electron rule. For instance, the K value of [CH] fragment = 1.5 which means this fragment requires only 3 (3+5 =8)electrons so as to obey the octet rule while for the fragment Ir(CO)₃ with the same K value of 1.5, it requires 3 electrons (3+15=18)so as to obey the 18 electron rule. Since the CH fragment and the Ir(CO)₃,have the same K value they are described as being isoloblal, that is, CH⥈Ir(CO)₃. This very important concept was introduced by Hoffmann based on molecular orbital theory [[29]. Selected isolobal chemical species are given in Table 4 and Scheme 1.

The isolobal lists can be expanded by adding analogous fragments or elements.

On the basis of the isolobal relationship, it is quite clear that the series of the main group elements or fragments are interrelated with those of the transition metal fragments. This may be expressed as

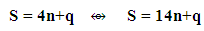where q is a variable or as indicated in Scheme 1.

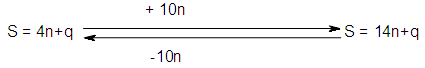This relationship was deduced in earlier work through the study of carbonyl clusters [18].

2.2.11. Derivation of Cluster Series from N-3 Tree

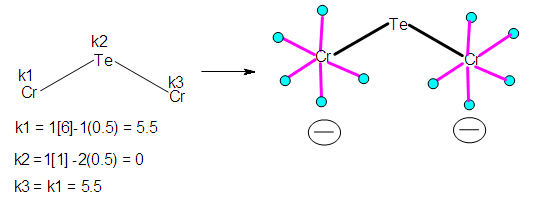
K(n) = 2(3) PARAMETER

Assigning ligands to skeletal atoms to produce a possible isomeric shape is one aspect, and the skeletal numbers can assist us. Let us consider two members of the branch, K (n) = 2(3), S = 4n+8 of the nuclearity N-3 tree below.

Ex-1 TeCr₂(CO)₁₀^2―, K = 1[1]+2[6]-10-1 = 13-11 = 2. Hence, K(n) = 2(3). With the K(n) parameter, we can derive the series and even derive the corresponding hydrocarbon and borane clusters although this approach has been discussed previously [13]. This is summarized and illustrated in Scheme 4.

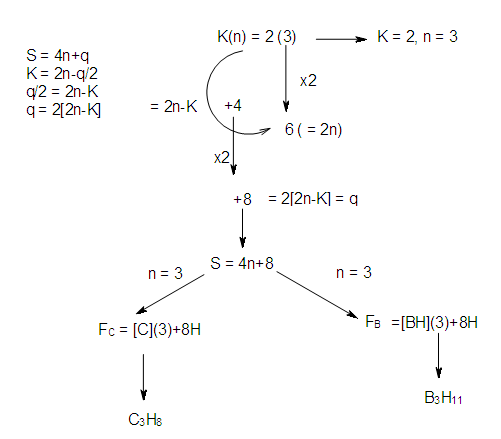Scheme 4. Short cut for Derivation of Series from K(n) Parameter

2.2.12. Geometrical Derivation from K(n) =2(3) Parameter

The distribution of ligands can also be accomplished using the skeletal numbers. This is also illustrated in Figures 4 and 5.

Figure 4. Using K value of a Skeletal Element to Distribute the Ligands

Figure 5. Using K value of a Skeletal Element to Distribute the Ligands

The calculation shows that for the chromium skeletal element to obey the 18 electron rule, it needs 5.5 electron pairs donated to it. This can be accomplished by receiving 5 CO ligands and one negative charge. Let us consider the distribution of the ligands in the cluster Re₃H₂(CO)₁₃^―, also with K(n) = 2(3).

2.2.13. Geometrical Derivation from N-6 Tree

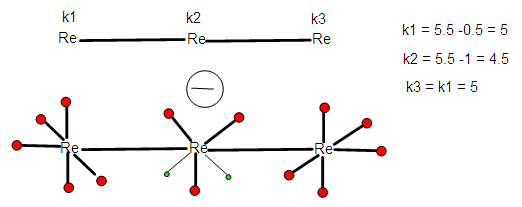
K(n) = 6(6)

Let us compare and contrast the skeletal structures of C₆H₁₂ and Re₆H₅(CO)₂₄^―, K(n) = 6(6), S = 4n+12. The hydrocarbon C₆H₁₂, and the rhenium cluster complex Re₆H₅(CO)₂₄^―, each possesses a cluster number of K = 6. This means that the six rhenium atoms will have 6 linkages. This is similar to the hydrocarbon C₆H₁₂. In principle, they are expected to portray similar geometrical shapes or isomers. It is not a surprise that it portrays the boat-shape form isomer of the C₆H₁₂ hydrocarbon as indicated in Figure 6.

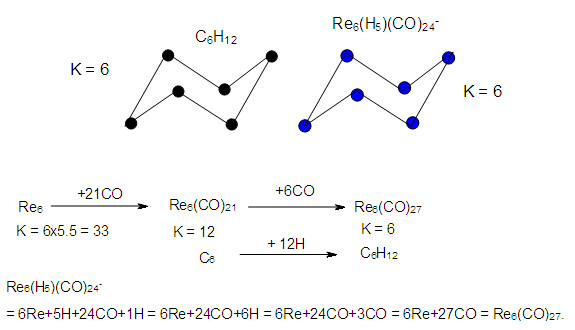Figure 6. Comparison of two Skeletal Shapes of Isomers for two clusters of the same K(n) Value

As can be seen from the Figure 6, and its associated scheme Re₆ +21CO →Re₆(CO)₂₁→C₆. Further addition of 6CO ligands to Re₆(CO)₂₁ produces Re₆(CO)₂₇. The cluster Re₆(CO)₂₇ corresponds to Re₆H₅(CO)₂₄^― complex which has the same K value as C₆H₁₂. In general, clusters with the same K(n) parameter tend to adopt an identical skeletal shape. This is illustrated by a few selected examples of clusters which have an ideal octahedral geometry. These are shown in Schemes 5 and 6.

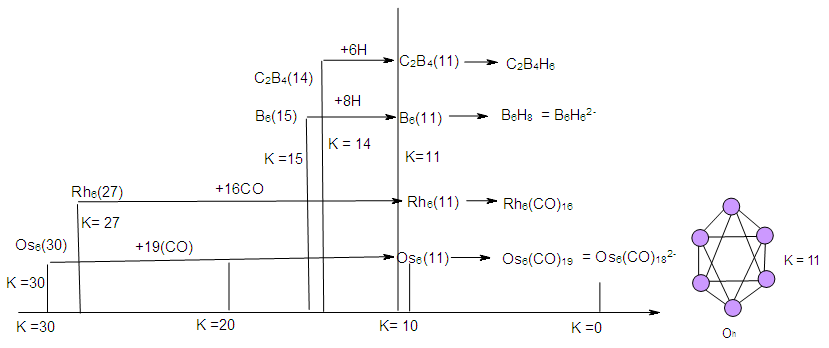Scheme 5. Selected Clusters with K(n) equal to 11(6)

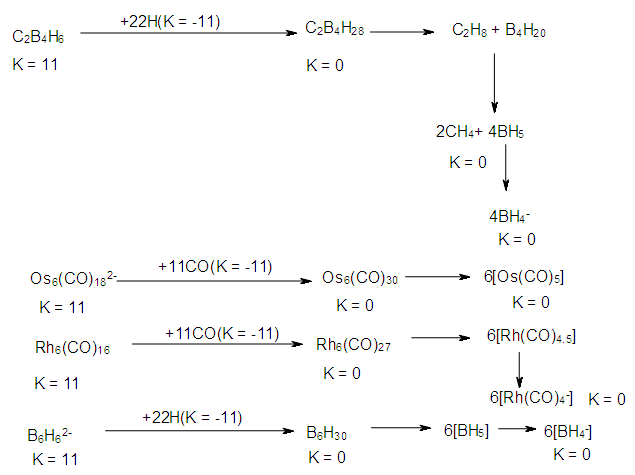Scheme 6. Conversion of K(n) of 11(6) to K(n) of 0(6)

Let us look at some more examples of N-6.

Ex-1

Ru₅(B)(CO)₁₅(AuL), L = PPh₃: K = 5[5]-1.5-15+1[3.5-1]= 11, K(n) = 11(6), q = 2{[2(6)-11}=2. Hence S = 4n+2, CLOSO series. The ideal shape is expected to be octahedral. What is observed [26] is sketched in Figure 7.

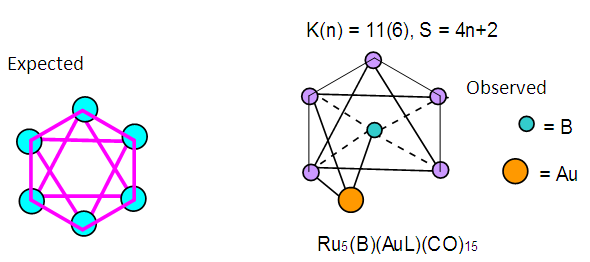Figure 7. Sketch of the ideal Octahedral Shape and the observed one

Since the cluster Ru₅₍B)(AuL)(CO)₁₅ has a K value of 11, it also needs 11 valence electron pairs in order to obey the 8 electron rule. In this cluster the B atom has been classified as a ligand. Let us make CO = L and B = L+H since it carries 3 valence electrons. We can set up a simple equation as follows: Ru₅₍B)(AuL)(CO)₁₅ + 11L →Ru₅(L+H)(AuL)(L)₁₅ +11L → 5Ru + 1Au+28L+H →5[RuL₅]+1[AuL₃H]. The complex RuL₅: K = 1[5]-5 = 0. Hence, it obeys the 18 electron rule. Also the complex, AuL₃H: K = 1[3.5]-3-0.5 = 0. This means the gold cluster also obeys the 18 electron rule. It should be pointed out that when an element such as boron is defined as a ligand, it donates 3 electrons to a cluster and its K = -1.5, whereas if it is taken as a skeletal element its K = 2.5.

Ex-2

Au₆L₆²⁺, L = PPh₃, K =6[3.5]-6+1 = 16, K(n) = 16(6); S = 4n-8, Kp = C⁵C[M-1], V = 14n-8, n = 6, V = 14(6)-8 = 76, From formula, V = 6[11]+6x2-2 = 76. This means one skeletal element at the nucleus surrounded by 5 capping elements. This is diagrammatically represented by Figure 8. An alternative shape is usually sketched as in Figure 9.

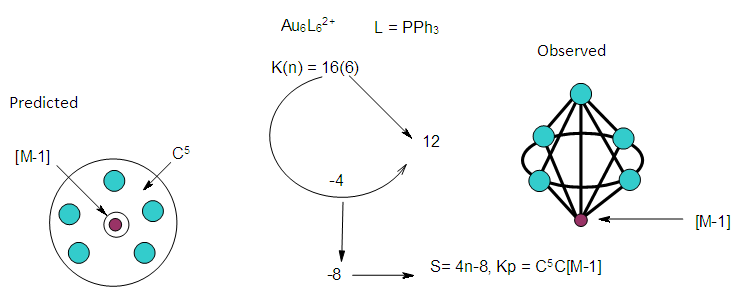Figure 8. The predicted shape and the observed shape of Au6L62+ cluster

Attempts are being made to emphasize the significance and meaning of the K value. In this light, the golden cluster Au₆L₆²⁺ has a K value of 16. That means if we donate 16 electron pairs to the cluster, all the 6 Au skeletal elements will obey the 18 electron rule. That is, Au₆L₆²⁺+ 16L→ Au₆L₂₂²⁺→ Au₆L₂₁→ Au₆L₁₈(H)₆ →6[AuL₃H]. The complex AuL₃H obeys the 18 electron rule.

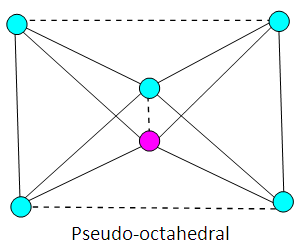Figure 9. An alternative sketch of Au6L62+ cluster

The skeletal shape is sometimes referred to as bi-tetrahedral.

Ex-3

(AuL)₅W(CO)₄⁺, L = PPh₃: K = 5[3.5-1]+1[6]-4+0.5 = 15, K(n) = 15(6), q = 2{[2(6)-15} = -6, S= 4n+q = 4n-6, Kp = C⁴C[M-2].

Assuming we started with Au₅W⁺ fragment, its K value will be given by K = 5[3.5]+1[6]+0.5 = 24. In order for this fragment to attain a K value of 15 we need to add on 9CO or 9L ligands. As can be seen from the formula (AuL)₅W(CO)₄⁺, there are 9 ligands involved, 5L+ 4CO. According to the series, this means that the two nuclear elements are connected by a triple bond. The expected skeletal shape is sketched in Figure 10. We can also test the concept of cluster K value = 15. Let us call two electron donor ligands which are in the cluster and to be added to the cluster as L and single electron donors as H = 0.5L. We can set up a simple equation as follows: (AuL)₅W(CO)₄⁺ + 15L→(AuL)₅W(L)₄⁺+15L →5Au+1W+24L-H= 5Au+1W+ 23.5L = 1[WL₆]+5Au+17.5L = WL₆+ 5[AuL_3.5] = WL₆+5[AuL₃H]. Each of the complexes WL₆ and AuL₃H obeys the 18 electron rule.

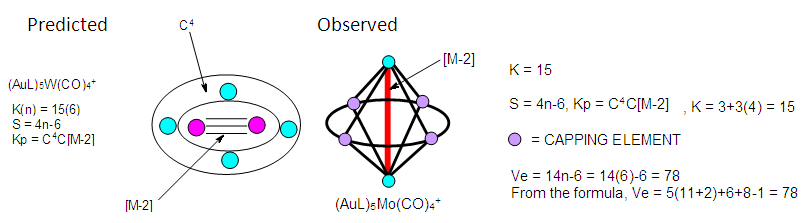Figure 10. Sketch of (AuL)5W(CO)4+ Cluster

2.2.14. The Meaning of the Cluster Number K Value As an Indicator of Electron Pair(s) Deficit

Let consider a few examples to illustrate this concept. Consider the cluster Rh₆(CO)₁₆, K =6[4.5]-16(1) = 11. Similarly, B₆H₆^2―, K = 6[2.5]-6(0.5)-1 = 11. In the above discussion, we regarded the K values as the electron pairs needed by the skeletal elements (except ligand donors) so as to obey the 8 or 18 electron rules. If we refer to the complex, Rh₆(CO)₁₆, it could be interpreted as the cluster requiring 11 electron pairs so as to fulfill the 18 electron rule. This means that if we could provide 11 CO ligands to the complex, all the skeletal elements will obey the 18 electron rule. Thus, Rh₆(CO)₁₆ + 11CO →Rh₆(CO)₂₇ cluster elements will obey the 18 electron rule. What does this mean? The complex, Rh₆(CO)₂₇ can be split into 6[Rh(CO)_4.5] ≡ 6[Rh(H)(CO)₄] or 6[Rh(CO)₄^―]. Amazingly, each of the above fragments obeys the 18 electron rule. It has also been shown above that B₆H₆^2― cluster obeys the 8 electron rule when 11x2H atoms are added. It is not a surprise that the skeletal shapes of both Rh₆(CO)₁₆ and B₆H₆^2― have an octahedral shape(O_h). Let us consider one more example, that is the octahedral complex, Os₆(CO)₁₈^2―, with a K value of 11. The complex also requires 11 electron pairs in order for all the 6 osmium skeletal elements to obey the 18 electron rule. Let us then add on the 11 CO ligands to the cluster as follows: Os₆(CO)₁₈^2―+11CO→Os₆(CO)₃₀. We can regard the two negative charges as equivalent to 1 CO ligand according to the 4n series approach. Clearly, Os₆(CO)₃₀ cluster system is equivalent to 6[Os(CO)₅]. As we know each of the Os(CO)₅ fragments obeys the 18 electron rule. Thus, Os₆(CO)₁₈^2―⥈ Rh₆(CO)₁₆⥈ B₆H₆^2― each with a K = 11. The K values of other molecules and clusters can be regarded in the same manner. For instance, C₂H₂, K = 3, means that the addition of 3 pairs of electrons or 6 hydrogen atoms to the two carbon skeletal elements will obey the octet rule. This is indeed the case, C₂H₂ + 6H →C₂H₈→2CH₄ and CH₄ obeys the octet rule. The complex Mo₂(Cp)₂(CO)₄, K = 2[6]-2(2.5)-4(1) = 3. This means the complex requires 3 pairs of electrons or their equivalents. This may be accomplished in a number of ways: Mo₂(Cp)₂(CO)₄+2CO+2e →2[Mo(Cp)(CO)₃^―] or Mo₂(Cp)₂(CO)₄ +η⁶-C₆H₆→ [η⁶-C₆H₆)Mo(CO)₃ + Mo(Cp)₂(CO)]. Each of the fragments, Mo(Cp)(CO)₃^―, η⁶-C₆H₆)Mo(CO)₃ and Mo(Cp)₂(CO) obeys the 18 electron rule. Table 8 shows a collection of clusters with their calculated K values. Each K value indicates the number of electron pairs needed to decompose the cluster into the mono-fragment clusters (N-1) which obey the 18 electron rule for transition metal elements. In the case of the main group clusters the derived N-1 clusters are expected to obey the 8 electron rule.

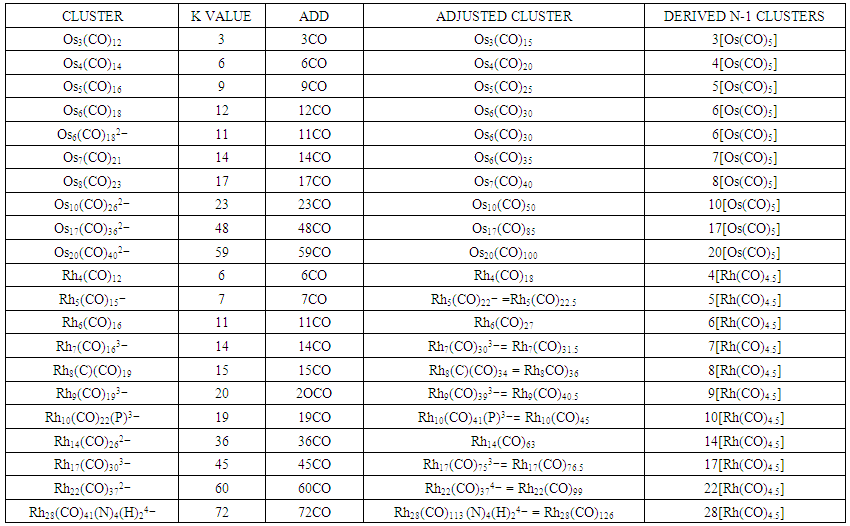Table 10. Demonstration of the Meaning of the Cluster Number for Selected Clusters

2.2.15. Ligands As Cluster Linkage Reducing Agents

From the analysis of cluster series, it is quite clear that in the addition of a ligand of any kind depending on the number of electrons it is donating, the original number of linkages are reduced accordingly. For every pair (2e) of electrons donated by a ligand, ONE skeletal linkage (∆K = -1) is removed from the skeletal cluster. Similarly, for every pair of electrons removed from the cluster, a skeletal linkage unit (∆K = +1) is added. Example, Os₆(CO)₁₈^2―(K =11)→Os₆(CO)₁₈(K = 12). For a capping cluster, as K increases, by one unit, the number of capping elements increases by one. The reverse is also true. As ligands are added successively to a cluster, the K value decreases more and more. The K value reaches a limit when K = n-1. Thus, for a cluster with two skeletal elements (N-2), the lowest K value = 1. For instance for C₂(K =4, n = 2) if H atoms are added, the lowest K value = 1 when C₂H₆ is attained. That is, C₂H₆ is expected to have a single bond which is the case. In the case of C₃ (K = 6, n = 3), is expected to have the lowest K = 2 when C₃H₈ is attained, that is, 2 linkages. For C₄(K = 8, n = 4), the lowest K value will be 3. This limit appears to apply regardless as to the nature of the skeletal element whether boron, carbon, osmium, chromium or gold. The initial K value of the cluster depends upon the skeletal number of the element. We have seen that C₂(K = 2x2 = 4), for Au₂(K = 3.5x2 = 5), and for Cr₂(K = 6x2 = 12). We have also seen that when the K value and the number of skeletal elements are the same, the geometry tends to be similar for all the clusters regardless of the nature of the skeletal element.

Examples; Fe₅(C)(CO)₁₄^2―, Fe₅(N)(CO)₁₄^―, Fe₅(C)(CO)₁₂L₃, Ru₅(C)(CO)₁₅, Os₅(C)(CO)₁₅, Re₅(C)(CO)₁₆(H)^2―, B₅H₉, Te₂Fe₃(CO)₉, Se₂Fe₂Mn(CO)₉^―, all belong to K(n) = 8(5), S = 4n+4 and the skeletal elements portray a square pyramidal shape.

2.2.16. Electron Counting: Effective Atomic Number (EAN)

A numerical number of valence electrons have been associated with a particular skeletal geometry. For instance, V = 48 for an N-3 cluster and 60, 72, 86 for tetrahedral, regular trigonal bipyramid and octahedral respectively [32]. An equation relating the effective atomic number electron count, the number of skeletal elements and the number of assumed skeletal linkages was developed. The equation is given by EAN = Valence electron content of the cluster = 18x-2y, x = number of skeletal elements, y = number of assumed skeletal linkages. The equation relates three variables. If two of them are known, then the third one can be calculated. A good example is Os₃(CO)₃, x =3, and y = 3. Hence, V = 18(3)-2(3) = 48. The formula also works well for Os₆(CO)₁₈, V = 18(6)-2(12) = 84. However, the equation does not work for clusters such as Os₃H₂(CO)₁₀, V = 46, Os₆(CO)₁₈^2―, V = 86. The good news is that by using K of the cluster from the series formula, the above formula works well for many types of clusters.

From the series method we know that S = 14n+q and K = 2n- ½ q. The valence electron content of a cluster is also calculated using the series formula if the value of the cluster is known. These two equations can be arranged in such way that we only have S in terms of n and K variables. Thus, q/2 = 2n-K, or q = 2[2n-K]. If this value is substituted into S = 14n+q, we get S = 14n+2[2n-K] = 18n-2K. This equation, S = V = 18n-2K is similar to EAN = V = 18x-2y given above except that the series formula uses n instead of x and K instead of y. Also S = 4n+q for main group clusters. If we substitute for q in this simple equation we get S = 4n+2[2n-K] = 8n-2K. Thus, V = 8n-2K for the main group elements. If we make K the subject of the simple equation, then K = ½ [8n-V] = ½ [E-V], where E = 8n for main group elements or K = ½ [E-V], where E = 18n for transition metal clusters. This relationship was empirically derived in earlier work [31] but is certainly linked to the series which were also empirically derived later [10]. A few examples are given in Scheme 7 below for the illustration purposes.

Scheme 7. Selected examples illustrating the calculation of Valence Electrons Using the Cluster Number Method

3. Conclusions

The skeletal numbers which were recently discovered have been extremely helpful in categorizing and predicting shapes of clusters. Further analysis has indicated that the skeletal numbers convey very important information. They actually indicate the deficit number of electron pairs a fragment, molecule or cluster requires for it to fulfill 8 or 18 electron rule requirement. The K(n) parameter lies at the intersection of lines of the series (∆K= ±2, ∆n = ±1), (∆K = ±3, ∆n = ±1) and (∆K = ±1, ∆n = 0). It has been found useful to categorize the clusters according to the series (∆K = ±1, ∆n = 0). This produces Nuclearity Cluster Trees. A movement along the nuclearity series gives us branches of trees which are themselves isolobal analogous series. The movement along the nuclearity tree provides important information regarding the changes in the geometrical configurations of the skeletal elements. The effective atomic number or simply cluster valence electrons can be calculated using the formula V=18n-2K for transition metal clusters or V = 8n-2K for main group elements, where n = number of skeletal elements, K = is the cluster number. The three important equations that were empirically derived during this work on clusters for some time, namely, S =14n+q/4n+q, K =2n- ½ q, and K= ½ [E-V] have now been interlinked in this paper. The calculation works perfectly well for the clusters encountered. The important K(n) Table was created and its meaning was explained and illustrated. It is quite clear that many clusters are formed according to the law of series (14n+q/4n+q).

As the skeletal elements and ligands can be assigned numerical values, fragments, molecules and clusters can easily and rapidly be categorized numerically.

ACKNOWLEDGEMENTS

The University of Namibia, and NAMSOV, Namibia are immensely acknowledged for the financial and material support rendered. Finally, my daughter, Dr. P. E. T. Kiremire for proof-reading the paper and my wife Merab Kambamu Kiremire for her continued encouragement to write up this work.

Dedication

This paper is dedicated to two among the great scientists of all time, namely, I. Langmuir and G. N. Lewis.