1. Introduction

Chemical clusters have fascinated scientists for a number of decades and they continue to do so [1-37]. During the study of chemical clusters, it was observed that the clusters follow consistent natural patterns (laws). The patterns have briefly been touched in previous work [30, 33]. After a careful scrutiny of the work on clusters, it has been found appropriate to clearly spell out these silent and important cluster patterns so that they can freely be utilized by scholars. These findings are summarized in this paper. It is proposed that we refer to them as rules or chemical cluster laws. The purpose of this paper is to briefly explain and highlight these laws.

1.1. Background

1.1.1. Origin of the 14n /4n Rule

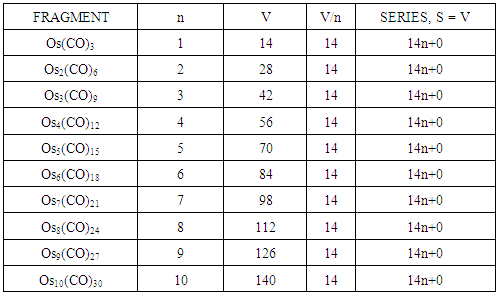
In an attempt to understand PSEPT concept [1, 2, 8, 10] and to find out if there is some order or disorder among clusters, a systematic study on osmium carbonyl clusters was carried out [32]. What was found interesting was that an osmium fragment, Os(CO)₃, with a content of 14 valence electrons [8+3x2] could be utilized as a starting point to generate as many hypothetical osmium clusters of different series as possible [33]. Multiples of the fragment, produced the same series S = V = 14n+0 (S = series, V = valence electrons). This is shown below.

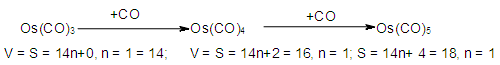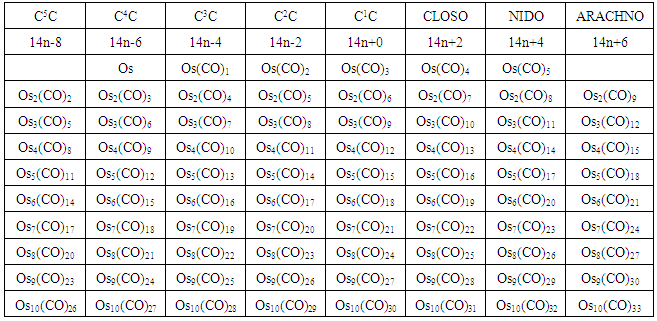
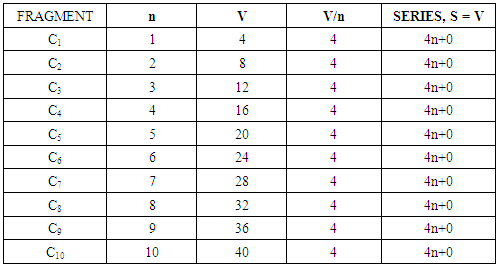
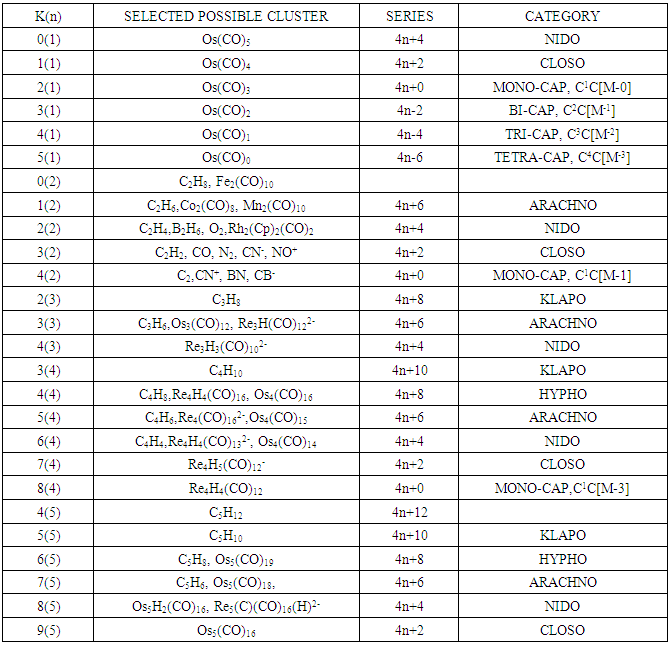
n = the number of skeletal atoms in a cluster.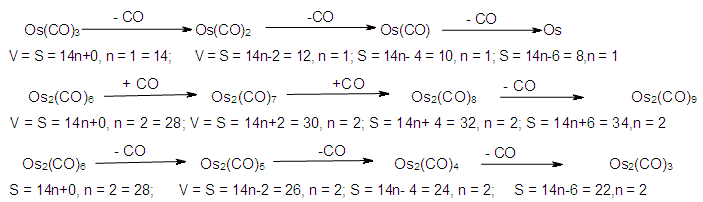

The derivation of selected the hypothetical carbonyl clusters of osmium of CLAN S = 14n+0 series are shown in Table-A and the capping and decapping series also generated using fragment F = Os(CO)₃ as a starting point are shown in Table-B. Under the column headed by C¹C are the same carbonyl clusters shown in Table-A. Also in Table-B shows a very important diagonal of cluster members Os₁₀(CO)₂₇, Os₉(CO)₂₃, Os₈(CO)₂₃, Os₇(CO)₂₁, Os₆(CO)₁₉[Os₆(CO)₁₈^2-, an octahedral complex]. The clusters before the octahedral complex are all capping series of the cluster geometry. The other two clusters in the diagonal namely, Os₅(CO)₁₇ and Os₄(CO)₁₅, correspond to the NIDO and ARACHNO members of the series. The hypothetical carbonyl clusters of rhenium, rhodium and palladium were similarly generated using the 14-electron fragments, Re(H)(CO)₃, Rh(H)(CO)₂, and Pd(CO)₂ respectively [32-33]. A search for a corresponding fragment of the MAIN GROUP ELEMENTS that could give the series S = 4n+0 was found to be [C] and the corresponding selected series are given in Table-C. These fragments are clearly isolobal, Os(CO)₃⥈ Re(H)(CO)₃⥈ Rh(H)(CO)₂⥈ Pd(CO)₂⥈C.

Table A. Derivation of S = 14n+0 Series

Table B. Generating the 14n Series

Table C. Derivation of S = 4n+0 Series of the Main Group Elements

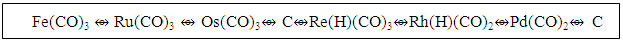Some of the carbon fragment series are shown below.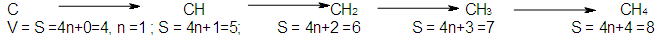

1.1.2. The Origin of the K- Value

Consider the following operations of fragments and series.

CH + CH → C₂H₂ → H―C≡C―H

4n+1(n =1) + 4n+1(n +1) → 4n+2(n + 2); K = 2n-1 = 2(2)-1 = 3

CH₂ + CH₂ → C₂H₄ → H₂C=CH₂

S = 4n+2(n =1) + 4n+2(n +1) → 4n+4(n + 2); K = 2n-2 = 2(2)-2 = 2

For C₂H₆, S = 4n+6, K = 2n-3 = 2(2)-3 = 1.

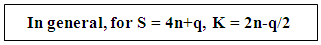
1.1.3. Isolobal Relationship

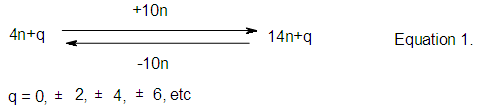
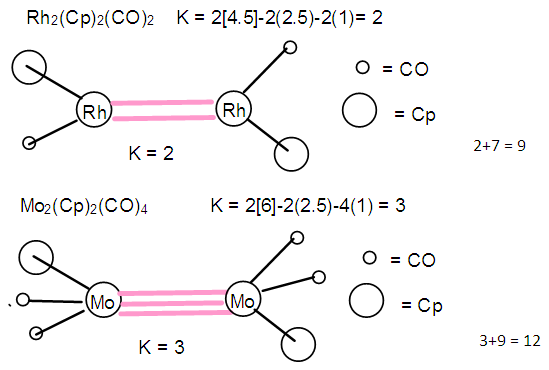
It was also found from the isolobal relationship [27] that 14n+q series behave in the same way as 4n+q. Furthermore, we could also apply the K = 2n-q/2 relationship to calculate cluster linkages in transition metal clusters. Let us consider Fe₂(CO)₉, S →2[Fe(CO)₃]+3CO→S = 14n+6(n= 2). This series also corresponds to S = 4n+6, hence K = 2n-3 = 2(2)-3 = 1. This means that the complex has one Fe―Fe bond. This cluster behaves in a similar was as C₂H₆ whose K= 1. Thus, Fe₂(CO)₉ ⥈ C₂H₆. If we consider another complex, Rh₂(Cp)₂(CO)₂. This can be fragmented into 2[Rh(Cp)]+ 2CO→S = 14n+4→S =4n+4 and K = 2n-2 = 2(2)-2 = 2. This implies the existence of a double bond, [Rh=Rh] in the cluster [24]. Lastly, the complex, Mo₂(Cp)₂(CO)₄→2[Mo(Cp)(CO)₂]→S =14n+2→S = 4n+2 and K = 2n-1 = 2(2)-1 = 3. This predicts the presence of [Rh≡Rh] triple bond in the cluster and this is indeed the case [24]. Furthermore, it was proposed instead of using 14n+q for transition metal clusters for analysis, we could as well, use 4n+q which is simpler except in cases where the value of valence electrons are required. More close studies of the series has recently led to the discovery of the SKELETAL NUMBERS. These have made the analysis and categorization clusters far much faster and easier. A good collection of background references of the origin of the laws is included under the author’s name. With this concise background on cluster series, it is hoped that the sifted cluster laws will be appreciated by our readers.

2. Results and Discussion

2.1. The First law: The 4n/14n law

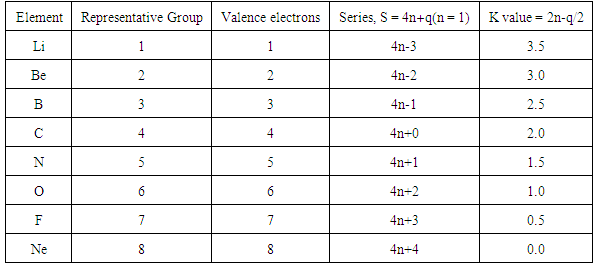
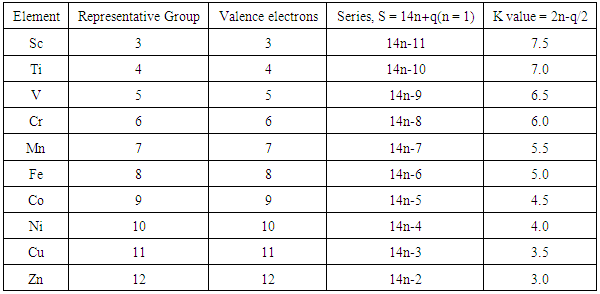
It has been found that the main group elements follow the 4n law (rule) while the transition metal elements follow the 14n law (rule) of clusters series. The 14n and 4n rules (series) were also used to categorize clusters [27-30]. As a consequence of this, the skeletal numbers which constitute the second law were derived [27-30]. Sample of selected elements are given in Tables 1 and 2 and their origin was discussed in previous work [27-30].

2.2. The Second Law: Skeletal Linkage Numbers and Their Periodicity

Table 1. Skeletal Numbers of the Main Group Elements (K values)

The skeletal numbers of the representative main group elements have been derived based upon the 4n series rule. Similarly, the skeletal numbers of transition elements were derived based upon the 14n rule [27-30].

2.2.1. Skeletal Numbers of Transition Elements (K values)

Table 2. Skeletal Linkage Numbers of Transition Metals

PERIODICITY is reflected in the skeletal numbers derived. For example in the case of main group elements (Table-1), starting with Li(K = 3.5), the K values decrease by K = 0.5 until Ne(K=0.0). The K = 0 for Ne is not a surprise as it is a member of inert gases of group 8. On the other hand, the transition metal elements start with Sc(K = 7.5) and decrease by K = 0.5 corresponding to an increase of one valence electron until Zn(K=3.0). Although the skeletal number has been derived for a representative element of a group, the other remaining elements (CONGENERS) have identical values. For instance as with Li (K = 3.5), the other elements Na, K, Rb, Cs have the same value. The same applies to group 2 to 8 as well as the transition elements. The skeletal number of one element differs from that of the next one by a value of 0.5. This pattern is periodic in nature. The series S = 4n+q (for main group elements) is related [25-26] to S = 14n+q (for transition metals) by the simple equation 1.

2.3. The Third Law: Conservation of Skeletal Numbers

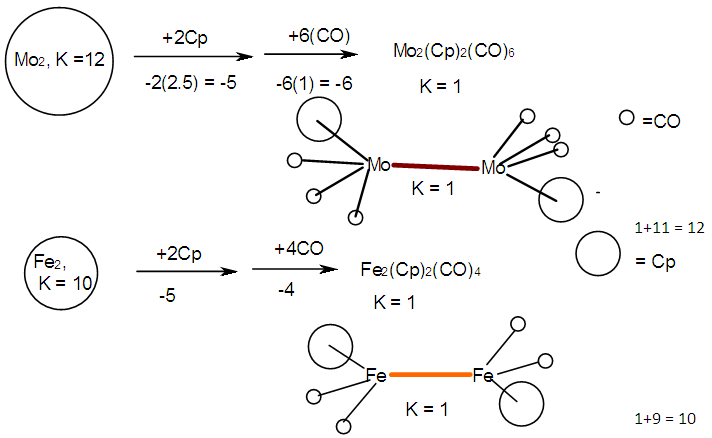
The conservation of skeletal numbers has already been discussed in previous work [30, 33-34]. In order to re-emphasize the concept, a few examples are given as illustrations in pictorial forms in Schemes 1 to 4.

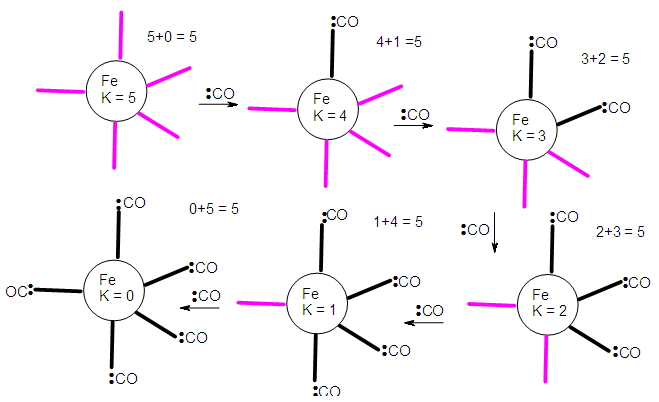Scheme 1. Demonstration of the law of conservation of skeletal linkage numbers by Fe fragments

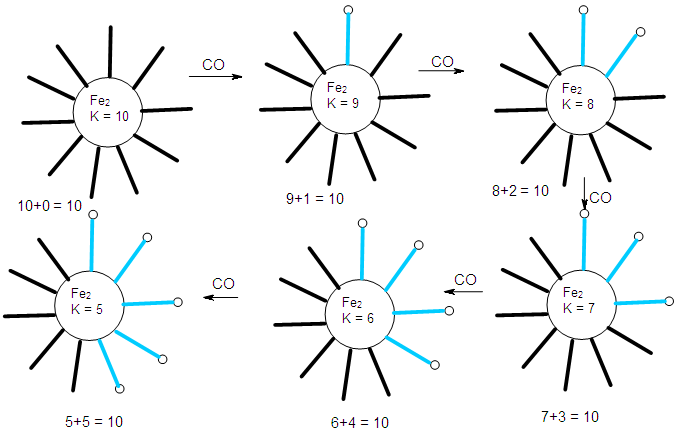Scheme 2. Conservation of skeletal linkage numbers of Fe2 cluster and its fragments

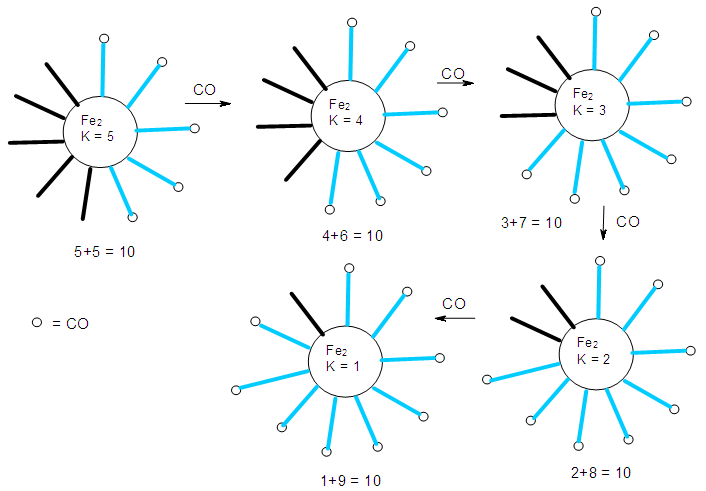Scheme 2. Continued

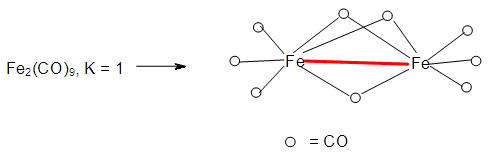Figure 1. Possible isomer of Fe2(CO)9 cluster

Scheme 3. More examples to demonstrate the Law of Conservation of Cluster linkages

Scheme 4. More examples on Conservation Law of Skeletal linkage Numbers

In the Schemes given above, in the case of one skeletal element Fe, the sum of skeletal linkages are always K = 5(see Table 2), while in the case of Fe₂, the sum K= 2x5 =10, Rh₂, sum K = 2x4.5=9 and Mo₂, sum is K =2x6=12.

IN SUMMARY, THE SUM OF SKELETAL LINKAGES DONATED TO THE LIGANDS BOUND TO THE CLUSTER AND THOSE RETAINED BY THE SKELETAL CLUSTER ARE EQUAL TO THE NUMBER OF SKELETAL LINKAGES ORIGINALLY PROVIDED BY THE INITIAL NAKED PARENT CLUSTER. If K₀ is the number of intrinsic linkages a naked parent cluster possesses, K_L the number of linkages donated to the ligands bound to the cluster, and K the number of linkages left after the donation to the ligands, then the LAW OF CONSERVATION OF SKELETAL LINKAGES CAN BE EXPRESSED BY THE SIMPLE EQUATION: K₀ = K_L+K.

2.4. The Fourth Law: The K(n)-Symmetry Linkage Law

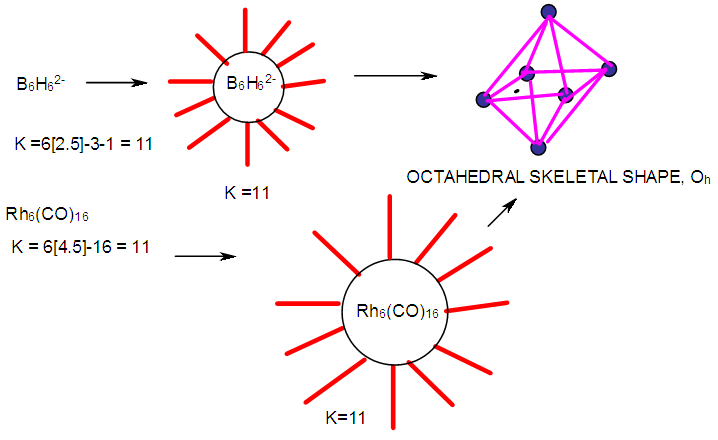
2.4.1 This simply means that a given K(n) parameter of a cluster can be associated with a certain skeletal cluster symmetry. The n stands for the number of skeletal elements and K represents the number of skeletal linkages corresponding to the cluster under consideration. For instance K(n) = 1(2), means that there are 2 skeletal elements linked by one bond. Such clusters belong to the series S = 4n+6(ARACHNO) (see Table 4). Examples include [6, 21] Mn₂(CO)₁₀, Fe₂(CO)₉, and C₂H₆. More examples can be found in Table 3. The K(n) = 2(2), means that 2 skeletal elements are linked by a double bond. It belongs to the series S = 4n+4(NIDO). Examples include, Rh₂(Cp)₂(CO)₂, C₂H₄, and O₂. On the other hand K(n) =3(2) means that 2 skeletal atoms are linked by a triple bond. The clusters belong to the series S = 4n+2(CLOSO). The examples include, C₂H₂, and Mo₂(Cp)₂(CO)₄. The K(n) = 6(4)→ represents an ideal tetrahedral symmetry. In this case, the cluster has 4 skeletal atoms and 6 linkages. It belongs to the series S = 4n+4(NIDO). Examples [6] include P₄, Ir₄(CO)₁₂ and InBi₃^2― (for more examples see Table 3). The ideal skeletal tetrahedral geometry for P₄ and Ir₄(CO)₁₂ is sketched in Figure 5. The parameter K(n) = 8(5) represents 5 skeletal elements and 8 linkages. It is the ideal geometry of a Square pyramid. It belongs to the series S = 4n+4(NIDO). Examples include [5, 6, 14] B₅H₉, C₂B₃H₇, C₅H₅⁺, B₃H₇(CoCp*)₂, Fe₅(C)(CO)₁₅, and Ru₅(C)(CO)₁₅ (for more examples see Table 3). The trigonal bipyramid geometry is represented by K(n) = 9(5) parameter. That is 5 skeletal elements with 9 linkages. Checking on Table 4 they are found to belong to series S = 4n+2(CLOSO). Examples include [5, 6, 31-32] B₅H₅^2―, Sn₅^2―, Bi₅³⁺, Te₂CrMo₂(CO)₁₀^2― and Os₅(CO)₁₅^2― (for more examples, see Table 3). Figures 2, 3 and 4 show linkage between K(n) and ideal symmetries of selected samples of clusters are given below. Figure 2[(iv)] focuses mainly on an ideal trigonal bipyramid symmetry. The octahedral geometry has code K(n) = 11(6) and is shown in Figure 4. The complexes with the ideal octahedral shape (see Figure 6), among others, include [34-37] Ru₆(C)(CO)₁₄(C₆H₆), Rh₆(CO)₁₆, Os₆(CO)₁₈^2-, Re₆(C)(CO)₁₉^2-, Co₄Ni₂(CO)₁₄^2-, Ru₆(H)(CO)₁₈^-, Ru₆(C)(CO)₁₈^-, TeRu₅(CO)₁₄^2-, HTeRu₅(CO)₁₄^-, Te₂Ru₄(CO)₁₁, Se₂Mn₄(CO)₁₂^2-, SFe₂Ru₃(CO)₁₄^2-, B₆H₆^2-, Os₆(H)(CO)₁₈^-, Re₆(C)(CO)₁₉(H)^-, Re₆(C)(CO)₁₉(H)^-, Re₆(C)(CO)₁₈(H)^3-, Re₆(C)(CO)₁₈(H)₂^2- and Re₆(H)₇(CO)₁₈^-.

We can regard every K(n) code to represent a particular structural geometrical shape or its corresponding isomer.

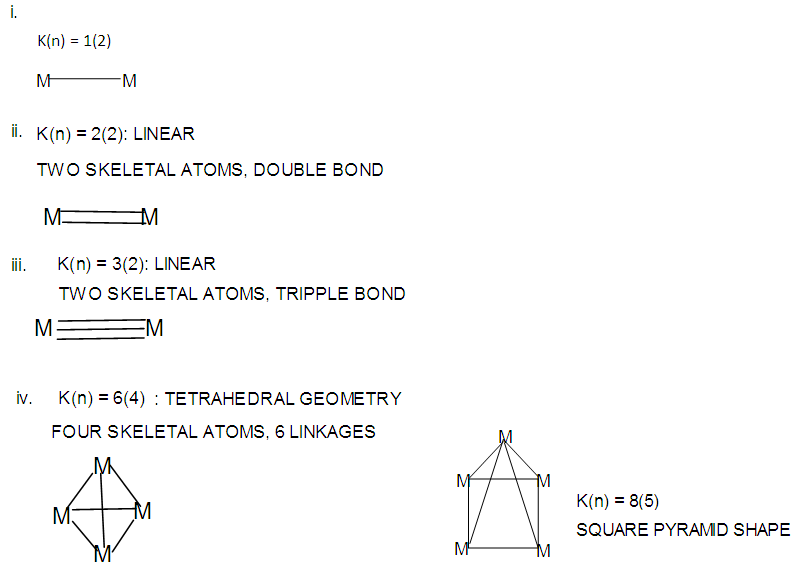Figure 2. Various geometries of selected skeletal clusters

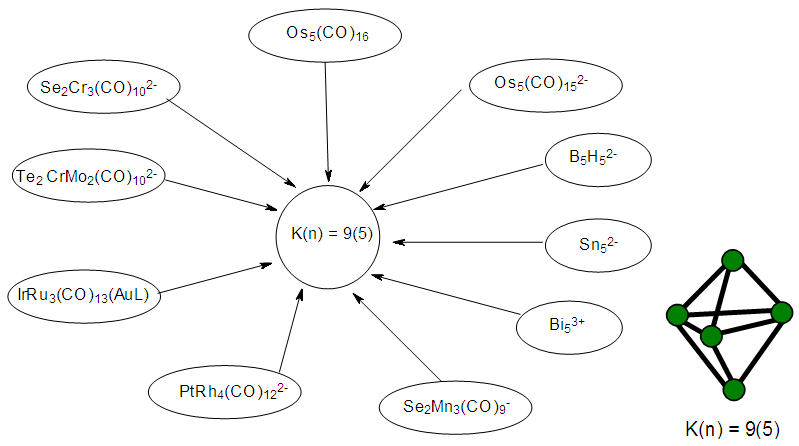Figure 3. Selected Clusters with Trigonal Bipyramid Shape

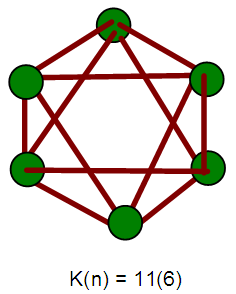Figure 4. An ideal skeletal octahedral Shape

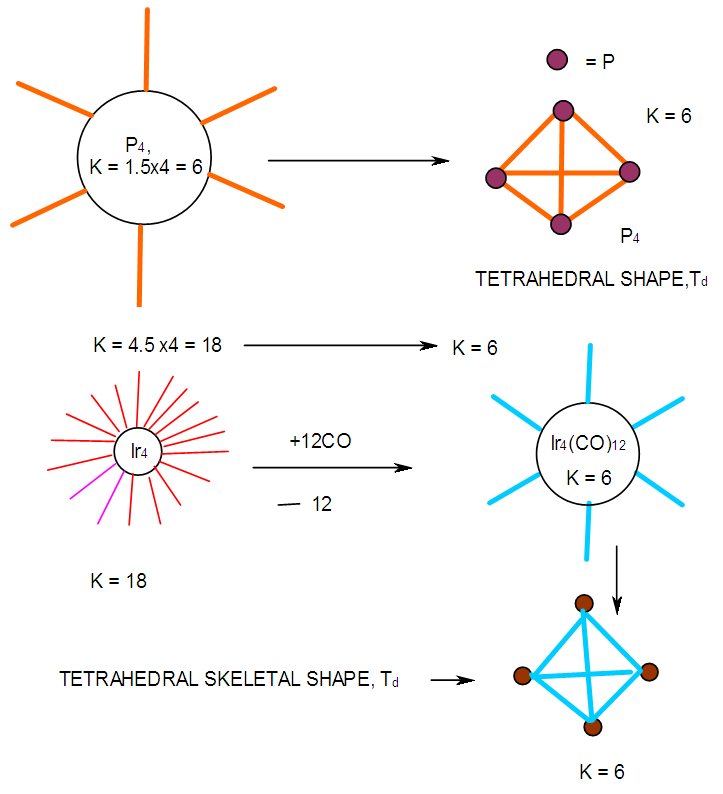Figure 5. Selected clusters with similar skeletal shape

Figure 6. Selected Clusters with similar skeletal shape

2.4.2. Compilation of K(n) Values

The K(n) values of a large number of clusters both small and huge have been compiled using skeletal numbers from Tables 1 and 2. These K(n) values are given in Table 3. After close scrutiny, it has been discovered that these K(n) values form a component of another Table 4 which was derived earlier [34]. Furthermore, the Table 4 can be utilized to greatly simplify the categorization of clusters. This will be illustrated in the last section of this paper.

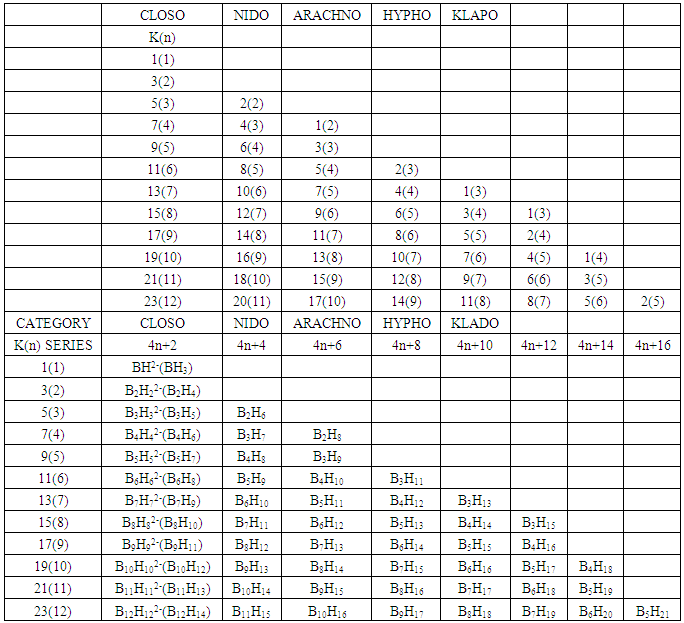
Table 3. Categorization of Clusters using K(n) parameter

Table 4. The K(n) Series for Cluster Categorization

2.4.3. Converting the K(n) Values into Clusters

Table 4 is extremely important as it unifies different types of chemical clusters. On the surface, it looks just like a set of numbers. Let us take an illustration by deriving a selected set of borane cluster series. In order for us to do this, we must derive some K(n) values that numerically depicts Rudolph’s system [3, 6]. This gives us Table 5. The K(n) values have been arranged in such a way that ∆K =3 for ∆n = 1 decrease occurs horizontally. The first column represents CLOSO family members of clusters from n =1 to n =12. The second column gives us the NIDO family, the third, ARACHNO, the fourth, HYPHO and the fifth, KLAPO and so on. We know that the S = 4n+2 series represents CLOSO family members. The closo members of borane series can be represented by a general formula F = [B_nH_n]^2-. The horizontal rows in Table 5 represent the cluster members of the Rudolph system which we now know from knowledge of series to be simply a portion of a wider universe of capping clusters. We can now proceed to translate the K(n) values in Table 5 into corresponding boranes. The K(n) = 1(1) means K = 1 and n =1. This simply means, the closo borane cluster has only 1 boron skeletal element and hence its formula corresponds to F = [B_nH_n]^2-= BH^2- =BH₃. Since the skeletal cluster value of boron is 2.5 (Table 1), the K value can be verified as K = 1[2.5]-1.5 = 1. As we have revealed from the Third Law above, a ligand ACTS AS A RECIPIENT OF CLUSTER LINKAGE VALUES FROM A SKELETAL CLUSTER DONOR ELEMENT. Thus for a one electron ligand donor like a hydrogen atom, [H•], the K value received = 0.5 resulting in a decrease of skeletal linkage content value of the skeletal cluster by K = 0.5. This concept is illustrated in Figure 7.

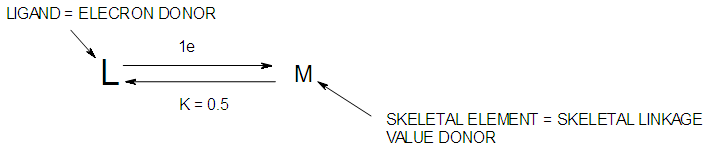Figure 7. Symbiotic relationship between a ligand and a skeletal element

Table 5. Converting selected K(n) Parameters into Borane Clusters

According to the series, there is no distinction between [H•] and [-1] charge, or [2H•] and [-2] charge, [:CO] or any other type of a 2-electron-donor ligand [: L]. Thus, the number of skeletal linkage values donated to the ligand(s) are directly proportional to the number of electrons donated by the ligand(s). THIS IS A TYPE OF ‘CHEMICAL SYMBIOTIC RELATIONSHIP’.

Hence, beyond BH₃ cluster, moving horizontally in Table 5 there is no meaningful cluster since the next K value will be 1-3 = -2 for n = -1. Moving to the left from 1(1), we get K(n) = 3(2), which represents F = B₂H₂^2- = B₂H₄. We can also verify its K value as K = 2[2.5]-1-1 = 3. The next K value horizontally in Table 5 will K = 3-3 =0. Again, this will give us a meaningless result. For K(n) = 5(3)→B₃H₃^2- = B₃H₅. Moving horizontally in Table 5, we get 5(3)→2(2), which generates B₂H₆ (diborane). In the next line in Table 5, we get K(n)→7(4)→4(3)→3(2). These K(n) values correspond to F = B₄H₄^2- = B₄H₆→B₃H₇→B₂H₈. This is followed by another row of clusters F = B₅H₅^2- = B₅H₇→B₄H₈→B₃H₉. The final example is F = B₆H₆^2- =B₆H₈→B₅H₉→B₄H₁₀→B₃H₁₁. The borane row of clusters according to Table 5 are produced simply by decreasing step-wise the number of boron atoms by one while increasing the hydrogen number of atoms by one on moving to the left. Other borane clusters can be generated in the same way. This means Table 5 has hypothetically generated Rudolph clusters, some of which are known and others not, using the K(n) values. Similar results were obtained earlier [26] using a different approach.

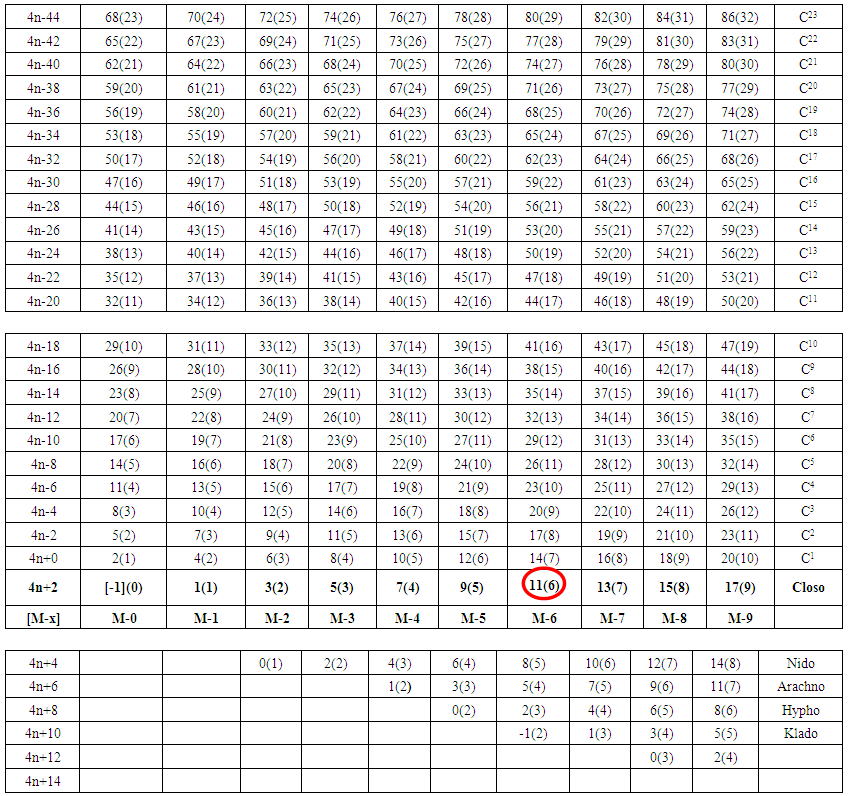
2.5. The Fifth Law. The Law of K(n) Correlation Series (Table 4)

2.5.1. The Fifth Law is the Basis of Table 4

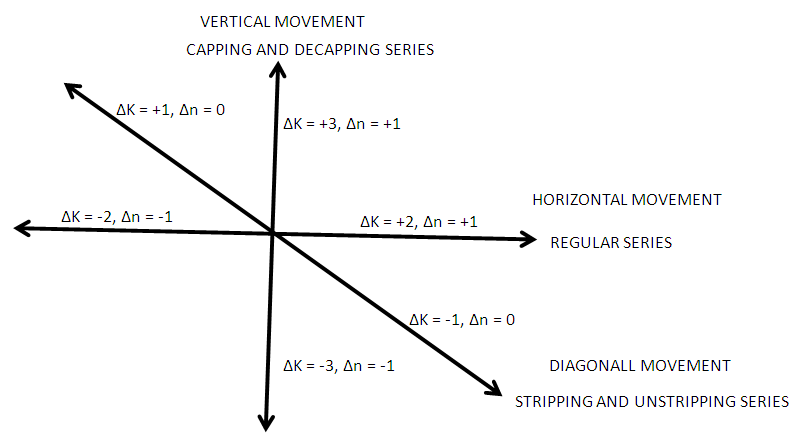
Taking K(n) = 11(6) as a starting point for illustration, the point 11(6) represents octahedral cluster symmetries. Moving upwards (VERTICAL MOVEMENT) from 11(6) we reach 14(7). That is, 11(6)→14(7). The point 14(7) represents a mono-capped octahedral shape, C¹C[M-6]. Examples include [35], Os₇(CO)₂₁ and Re₇(C)(CO)₂₁H₂^-. Further movement upwards gives the next point 17(8). That is, 14(7)→17(8). This gives us a bi-capped octahedral cluster, C²C[M-6]. Examples include [35] and Re₈(C)(CO)₂₄^2-, and Os₈(CO)₂₂^2-. Let us consider HORIZONTAL MOVEMENT TO THE RIGHT from 11(6). This will give the point 13(7) and the next point will be 15(8). On the other hand moving to the LEFT we get 9(5). That is, 9(5)←11(6). The point 9(5) represents the ideal geometry of trigonal bipyramid clusters. Both 9(5) and 11(6) belong to 4n+2 series (CLOSO). Let us consider the DIAGONAL MOVEMENT going to the left. From 11(6) we reach 12(6). That is, 11(6)→12(6). The next point is 13(6). The process gives rise to continuous capping series of a cluster without varying the number of cluster elements. Moving from 11(6) DIAGONALLY to the right gives the point 10(6) and the next point is 9(6). Whereas 11(6) code normally represents an OCTAHEDRAL GEOMETRY, the point 9(6) normally represents the ideal skeletal shape of TRIGONAL PRISM CLUSTERS (see Figure 7). Benzene, C₆H₆[K(n) =9(6) and prismanes C₆R₆[(R = H, alkyls or aryls, K(n) = 9(6)] also portray trigonal bipyramid prism geometry [37]. Other examples include [37], Rh₆(C)(CO)₁₅^2- and Rh₆(N)(CO)₁₅^-. The three important types of correlations are sketched in Figure 8. These three types of cluster series are discussed in more details below.

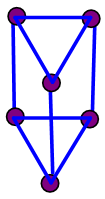Figure 7. Ideal skeletal shape of a trigonal bipyramid prism geometry

Figure 8a. Three Major Types of K(n) series

Figure 8b. Continuation

2.5.2. The Vertical Movement in Figure8, Table 4, ∆K = 3, and ∆n = 1, Capping Series (Rudolph Series)

Let us use the code K(n) = 11(6) as a reference point in Figure 8. The code sequence as we move upwards from the center will be as follows, 11(6)→14(7)→17(8)→20(9)→23(10)→26(11)→ 29(12)→ 32(13) and so on. These represent the capping series for an octahedral geometry. From 14(7), that is a code for a mono-capped octahedral cluster with a symbol, C¹C[M-6]. Examples include [38] Os₇(CO)₂₁ and Re₇(C)(CO)₂₁^3-. The next, 17(8) represent a bi-capped octahedral cluster, C²C[M-6]and examples include [35] Re₈(C)(CO)₂₄^2- and Os₈(CO)₂₂^2-. With the third one, C³C[M-6], a tri-capped octahedral cluster, examples are [35] Os₉(CO)₂₄^2- and Rh₉(CO)₁₉^3-, and the code C⁴C[M-6] represents a tetra-capped octahedral cluster. The examples include [38] Os₁₀(CO)₂₆^2- and Rh₁₀(CO)₂₁^2-, and so on. If we go vertically down below K(n) = 11(6), we get K(n) = 8(5). Examples were given under the Fourth Law above. We can regard this code to represent a square pyramid geometry. If we carefully examine the vertical movements along the code numbers, we see clearly that we are actually reproducing and extending the vital concept observed by Rudolph [3] in his scheme widely utilized to categorize mostly borane clusters and their relatives.

2.5.3. The Horizontal Movement in Figure 8, ∆K = 2 and ∆n = 1, Ordinary Series

Let us use the same code K(n) = 11(6) as our reference point for the illustration of horizontal movement according to Figure 8 and Table 4. Moving to the right from 11(6), we get the following sequences: 11(6)→13(7)→15(8)→17(9)→19(10), etc as mentioned above. On moving to the left we get: 11(6)→9(5)→7(4)→5(3)→3(3)→1(2). All these K(n) values belong to the same series S = 4n+2(CLOSO family). The code K(n) = 9(5) represents an ideal skeletal shape of a trigonal bipyramid as indicated in Figure 3. Examples were also mentioned under the Fourth Law. The code 3(3) usually represents an ideal triangular shape (∆) and 1(2) represents the ideal shape of two skeletal elements linked by one bond is shown in Figure 2[(i)].

2.5.4. The Diagonal Movement in Figure 8, ∆K = 1 and ∆n = 0, Stripping Series

Let us consider a series of K(n) values where n is kept constant. Moving along the diagonal from the right beginning with 0(1), the next is 1(1) followed by 2(1), 3(1), 4(1) and 5(1); this could represent the stripping series of Fe(CO)₅ (Scheme 1). The K(n) variations with n constant can be presented as a diagonal movement in Table 4. The constant n values may be regarded as ‘HIGHWAYS’. Thus, we have tabulated the selected highway values, n = 1, 2, 3, 4, 5, up to 32 shown in Table 4, which can be extended as desired. Selected examples of clusters lying on highways from n= 1 to n= 5 are given in Table 6. Let us use the code 11(6) as a reference point once more. A lot of good work on stripping series has been done by several research groups [16-19]. Some of the complex systems studied include: H₃Ru₄(CO)₁₂^―, K(n) = 6(4)→HRu₄^―, K(n)=19(4); PtRu₅(C)(CO)₁₅^2―, K(n) =11(6) →PtRu₅(C)(CO)₈^2―, K(n) = 18(6); Os₁₀(C)(CO)₂₄^2―, K(n) = 23(10)→Os₁₀(C)^2―, K(n) = 47(10); Pd₆Ru₆(CO)₂₄^2―, K(n) =29(12)→Pd₆Ru₆^2―, K(n)=53(12) and Os₂₀(CO)₄₀^2―, K(n)=59(20)→Os₂₀^2―, K(n) =99(20). Taking the stripping series of K(n) = 6(4)→19(4){H₃Ru₄(CO)₁₂^―, K(n) = 6(4)→HRu₄^―, K(n)=19(4)} as an example, we get 6(4)[S=4n+4]→7(4) [S=4n+2] →8(4) [S=4n+0] →9(4) [S=4n-2] →10(4) [S=4n-4] →11(4) [S=4n-6] →12(4) [S=4n-8] →13(4) [S=4n-10] →14(4) [S=4n-12] →15(4) [S=4n-14] →16(4) [S=4n-16] →17(4) [S=4n-18] →18(4) [S=4n-20] →19(4) [S=4n-22. Of great importance is that, when the diagonal relationship is analyzed carefully, all the K values of clusters with the same skeletal number of elements (n) lie along the same diagonal. For example, Ni₆(Cp)₆, K(n) = 9(6), Rh₆(CO)₁₅(C)^2-, K(n) = 9(6), Re₆H₈(CO)₁₈^2-, K(n) = 10(6), Rh₆(CO)₁₆, 11(6), and Os₆(CO)₁₈, K(n) = 12(6). The order is 9(6)→10(6)→11(6) →12(6). That is, the diagonal ‘Highway’ is along n = 6. Take another example, K(n) = 4(5)[C₅H₁₂]→5(5)[C₅H₁₀] →6(5)[C₅H₈] →7(5)[Rh₅(CO)₁₅^―]→8(5)[B₂H₆Ru₃(CO)₉, C₂B₃H₇,B₅H₉] →9(5)[B₅H₅^2-, Sn₅^2-,Os₅(CO)₁₆, Se₂Cr₃(CO)₁₀^2-]→10(5) →11(5) →12(5)[(AuL)₄Re(CO)₄⁺]. All these clusters are found lying along a diagonal highway n = 5 in Table 4. More examples of clusters that lie along the same diagonal are given in Table 6.

2.6. Cluster Hole Formalism

The stripping of CO ligands from the cluster Os₁₀(C)(CO)₂₄^2―, K(n) = 23(10){4n-6→C⁴C[M-6]} to Os₁₀(C)^2―, K(n) = 47(10){4n-54→C²⁸C[M-¹⁸]} cluster involves the loss of 24 CO ligands. According to series, this means an increase of K values by 24 units. As expected, the new K value will be 23+27 = 47. Hence, the K(n) values will follow the increasing trend as follows: 23(10)→24(10)→25(10)→26(10)→27(10)→28(10)→ 29(10)→30(10)→31(10)→32(10)→ 33(10)→34(10)→ 35(10)→36(10)→ 37(10)→38(10)→39(10)→40(10)→ 41(10)→42(10)→43(10)→44(10)→45(10)→46(10) →47(10) Øcorresponds to S = 4n-54→Cp = C²⁸C[M^-18]. Since we know that the cluster has 10 skeletal elements, and the capping symbol states there are 28 capping elements, this could possibly be translated as 10 skeletal elements co-existing with ‘18 holes’. It is likely that the presence of such holes in a cluster promotes the flow of electrons and hence electrical conductivity.

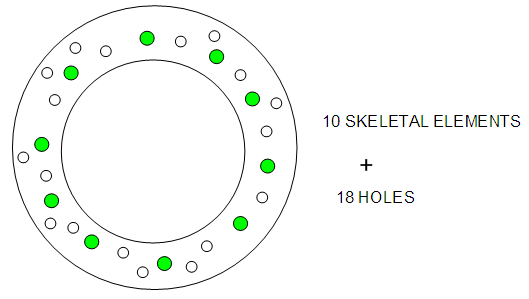Figure 9. Shows the possible presence of capping holes in the clusters

The process of stripping of CO ligands from Os₁₀(C)(CO)₂₄^2― cluster to generate holes may be represented by the diagram shown in Scheme 5.

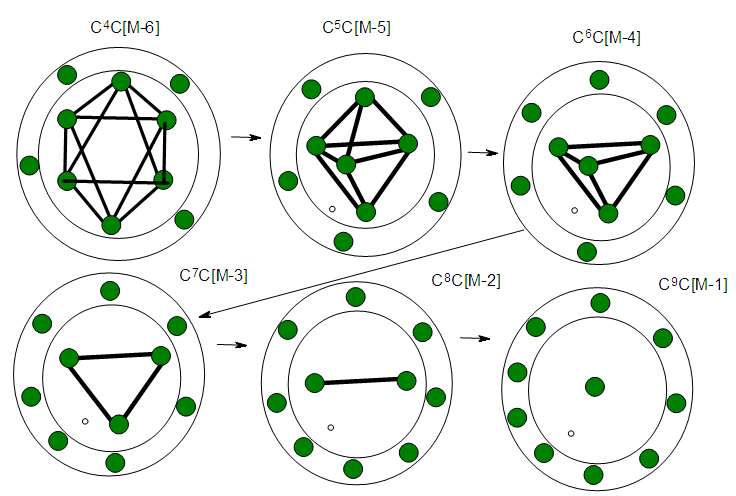Scheme 5. Shows increase in Capping with increased stripping of CO ligands

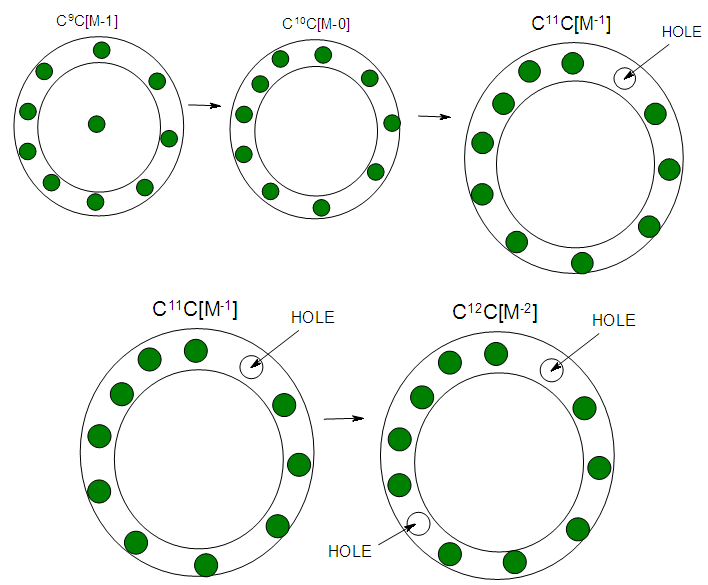Scheme 5. Continued

Table 6. Selected clusters which are located on the same n highway

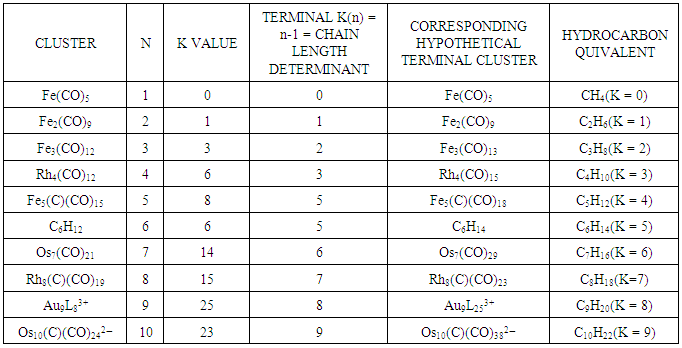
2.7. The Sixth Law: The Cluster Chain Length

The chain length of a cluster M_n (n = number of skeletal elements) terminates when K = n-1. Scheme 6 gives a few examples to demonstrate the concept of cluster termination (saturation) point.

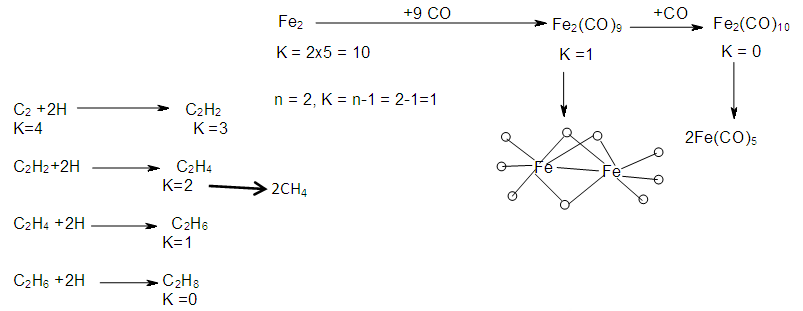Scheme 6. Creation of Cluster Chain Length

Let us consider the above examples in more detail, starting with C₂ cluster. If we add ‘2H ligands’ step-wise, the K value will be reduced by 1 step-wise.

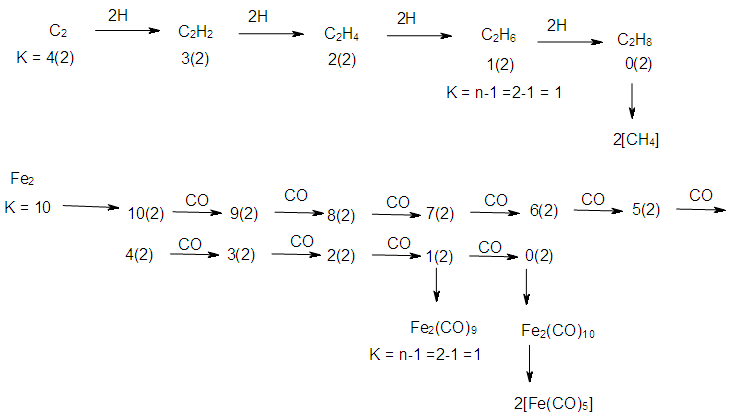Scheme 7. Stepwise decrease of K values with addition of ligands for a hydrocarbon and metal carbonyl cluster

Let us represent a skeletal element by (E). A single skeletal element E₁ will attain saturation point at K = n-1 = 1-1 = 0, when a cluster obeys 18-electron rule. If the naked cluster comprises of two skeletal elements E₂, the chain length reaches a saturation point at K = n-1 = 2-1 = 1. However, when the cluster of two skeletal elements goes beyond K = 1, decomposition takes place as in case of C₂H₆ or Fe₂(CO)₉. This is shown in Scheme 7. The development of chain length of Fe₃ which terminates at K = n-1 = 3-1 =2 is shown in Scheme 8. The K values of the termination of the chain lengths of selected clusters is given in Table 7.

The addition of a ligand to a skeletal cluster leads to a decrease of skeletal number (K) value. The removal of a ligand from a skeletal cluster leads to an increase in K value. This also applies to charges. The addition of a negative charge (-1) leads to a decrease of K value by 0.5. This is similar to the addition of an H atom. The removal of a charge from a cluster leads to an increase of K value by 0.5. This is similar to oxidizing a cluster by (+1). By studying series it was found that the more ligands are added to the naked cluster, the further the K value decreases. This goes on until a saturation point is attained. In principle, it has been observed that a naked cluster [X_n] with n = the number skeletal atoms of element X, will have TERMINAL SKELETAL LINKAGES SIMILAR to that of corresponding SATURATED HYDROCARBON [C_nH_2n]. This phenomenon has been observed in previous work [42]. A sample of selected clusters is given in Table 7.

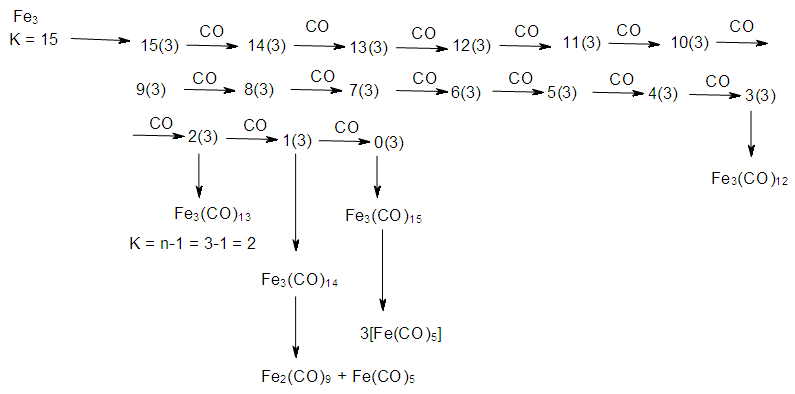Scheme 8. Possible Mechanism for cluster formation of Fe3 cluster chain length

Table 7. Selected clusters showing their corresponding chain lengths

2.8. Categorization of Clusters Using Table 4

Categorization of clusters using skeletal numbers and series has been discussed before [28-31]. However, in this paper categorization using cluster number (K value) and Table 4 will be applied. In the examples given below, the Law of conservation of cluster linkages is applied. They show the ease and quick approach to the derivation of cluster K values and their application with Table 4 to categorize clusters.

1. Co₆(C)(CO)₁₂(AuL)₄

K =6[4.5] +4[2.5]-2-12 = 23→23 (10)→ S =4n-6 (from Table 2), Cp = C⁴C[M-6]. This means the cluster belongs to the tetra-capped series [36]. It has an octahedral nucleus as sketched in Figure 10.

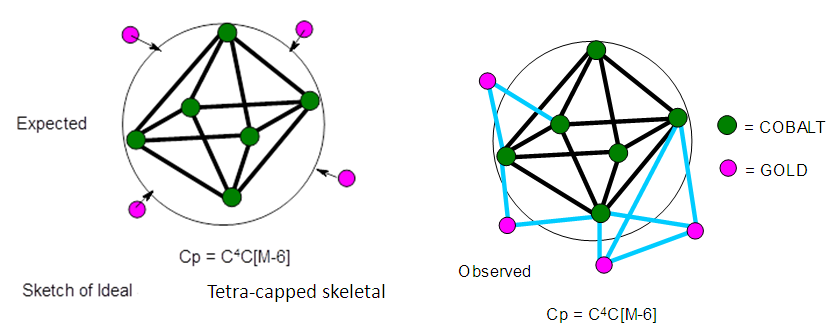Figure 10. Possible shape of a tetra-capped skeletal octahedron

2. Pt₅(CO)₆(PR₃)₄

K =5[4]-6-4 =10→10(5)→S = 4n+0, Cp = C¹C[M-4]. This means that the skeletal shape will have 4 skeletal atoms as a nucleus and one of the atoms will be capping [36]. This is shown in Figure 11.

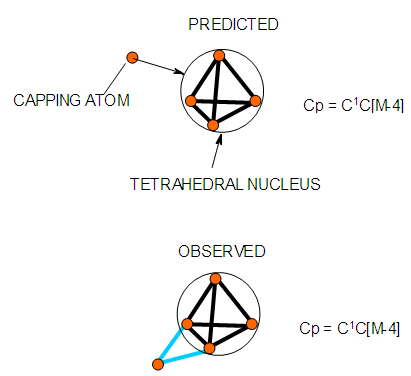Figure 11. Possible shape of a mono-capped tetrahedron

3. Co₅(C)(CO)₁₁(AuL)₃

K =5[4.5] +3[2.5]-2-11 = 17→17(8)→S =4n-2, Cp = C²C[M-6]. This means the ideal skeletal shape will be a bi-capped octahedral [36]. This is shown in Figure 12.

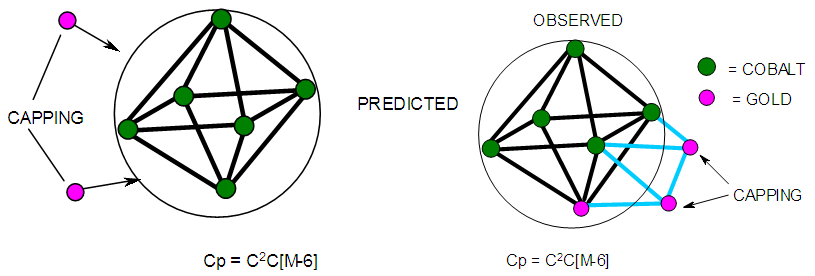Figure 12. Possible shape of a bi-capped octahedral shape

4. Fe₅(C)(CO)₁₄(AuL)₂

K= 5[5] +2[2.5]-2-14 = 14(7)→S = 4n+0, Cp = C¹C[M-6]. This means that the cluster is a mono-capped octahedral [36] as shown in Figure 13.

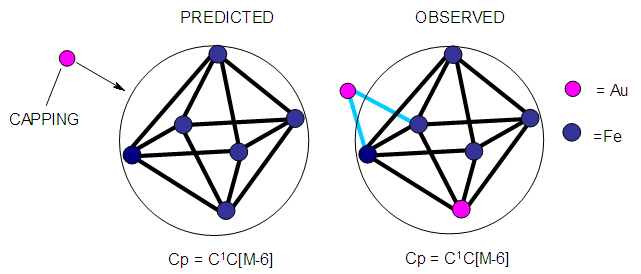Figure 13. Possible shape of a mono-capped octahedral shape

5. Pt₁₃(CO)₁₂^8-

K = 13[4]-12-4 = 36→S = 4n-20 (see Table 7), Cp = C¹¹C[M-2]. This is a cluster with a nucleus of 2 elements and capped 11 times [36]. This is sketched in Figure 14.

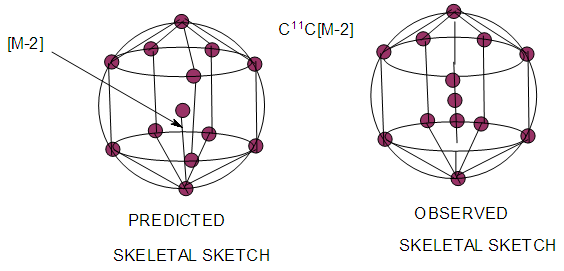Figure 14. A cluster with a nucleus containing two skeletal atoms

6. Pt₁₉(CO)₂₂^4-

K = 19[4]-22-2 = 52→52(19)→S =4n-28(from Table 4). Cp = C¹⁵C[M-4]. This means there 15 skeletal elements capping around 4 other skeletal elements acting as a nucleus [36]. This is sketched in Figure 15.

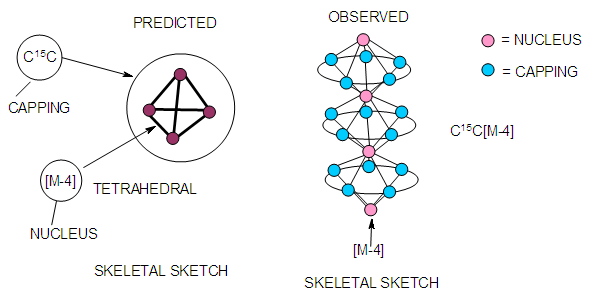Figure 15. A cluster with an ideal centered tetrahedral skeletal nucleus

7. IrRu₃(CO)₁₃(AuL)

K = 1[4.5] +3[5] +1[2.5] -13 = 9→K(n) = 9(5). Ideal shape is TRIGONAL BIPYRAMID, S = 4n+2(see Table 7, CLOSO). The predicted ideal shape [39] is shown in Figure 16.

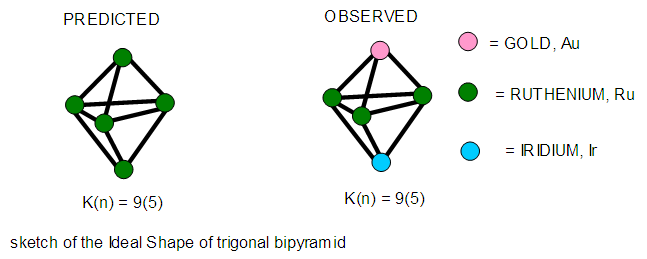Figure 16. Sketch of an ideal trigonal bipyramid shape

8. HIrRu₃(CO)₁₂(AuL)₂

K = 1[4.5] +3[5] +2[2.5]-12-0.5 = 12→12(6), S = 4n+0, Cp = C¹C[M-5]. The cluster is a mono-capped trigonal bipyramid [39]. This is sketched in Figure 17.

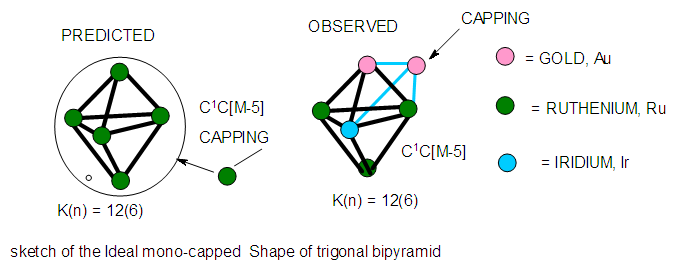Figure 17. Sketch of an ideal mono-capped trigonal bipyramid cluster

9. IrRu₃(CO)₁₂(AuL)₃

K = 1[4.5] +3[5] +3[2.5]-12 = 15(7)→S =4n-2,Cp = C²C[M-5]. The cluster has a trigonal bipyramid nucleus which is bi-capped [39]. This is shown in Figure 18.

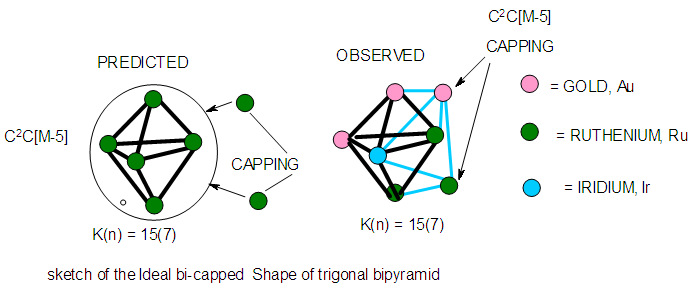Figure 18. Sketch of Ideal bi-capped trigonal bipyramid cluster

10. Co₁₁(N₂)(CO)₂₁^3-

K =11[4.5]-5-21-1.5 = 22→22(11), S =4n+0, Cp = C¹C[M-10]. The cluster comprises of a nucleus of 10 skeletal elements and these are capped with one skeletal element according to the series. The [M-10] nucleus is a member of CLOSO series. Hence, [M-10] corresponds to B₁₀H₁₀^2-. The predicted and observed skeletal structures [40] are shown in Figure 19.

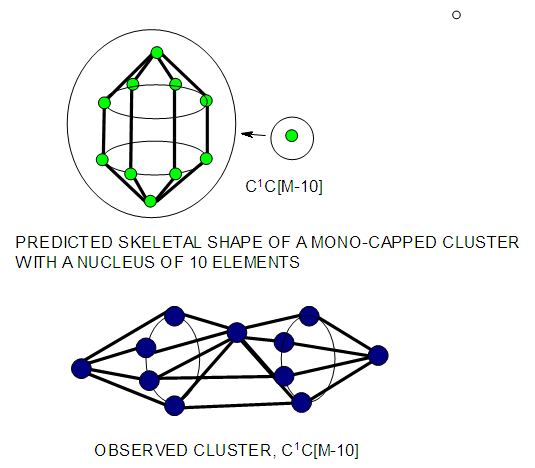Figure 19. Ideal mono-capped cluster with a 10 skeletal atom nucleus

11. N_i38Pt₆(CO)₄₈(H)^5-

K = 38[4] +6[4]-48-0.5-2.5 = 125→ K(n) = 125(44), S = 4n-74, Cp = C³⁸C[M-6]. This symbol predicts a giant cluster with 6 skeletal atoms at the nucleus arranged to form an octahedral and surrounded by 38 capping elements [40]. This is what is observed and is sketched in Figure 20.

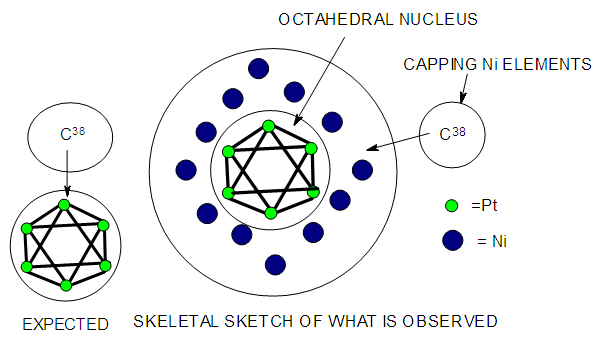Figure 20. Sketch showing a giant cluster with an octahedral nucleus

3. Conclusions

The six simple rules or laws of chemical clusters will make it much easier to analyze and categorize a wide range of clusters using skeletal linkage values and the K(n) parameter. Furthermore, the geometries of some clusters could readily be predicted. The skeletal cluster hole formalism concept has been introduced. The categorization of clusters using the K(n) parameter and the cluster mapping format in Table 4 has been demonstrated. The clear identification of the six rules or laws underpins the great importance of the use of the Series method, which could be applied to explain more complex clusters. These six chemical cluster laws are being unambiguously pronounced for the first time in the history of clusters.

ACKNOWLEDGEMENTS

I wish to acknowledge the University of Namibia for providing the facilities and enabling environment to do this work and NAMSOV, NAMIBIA for financial support. Further, I wish to thank Dr. P.E. T. Kiremire and Mrs M.K. Kiremire for proof-reading the draft.