-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Chemistry
p-ISSN: 2165-8749 e-ISSN: 2165-8781
2015; 5(2): 55-59
doi:10.5923/j.chemistry.20150502.02
Prediction of Reaction Mechanism of Displacement Reactions at Thiocarbonyl Substrates
Shuchismita Dey
Department of Textile Engineering, Southeast University, Tejgaon, Dhaka, Bangladesh
Correspondence to: Shuchismita Dey, Department of Textile Engineering, Southeast University, Tejgaon, Dhaka, Bangladesh.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
The nucleophilic displacement reactions at thiocarbonyl center have been considered in wide variety in organic Chemistry. The reactions proceed through stepwise process with tetrahedral intermediate in rate limiting step. This mechanism has been interpreted in various reaction systems such as the reactions of secondary alicyclic amines with the Phenyl and Methyl 4-Nitrophenyl Thionocarbonates, Aminolyses of O-4-Nitrophenyl Thionobenzoate with Primary and Secondary Amines etc. More examples are Kinetics and Mechanism of the Pyridinolysis of Alkyl Aryl Thionocarbonates, Kinetics of the Aminolysis of Thionocarbonates etc. In the course of reaction of aminolysis of thionocarbonates Castro et al. proposed that the general base catalysis by amine found in the aminolysis of NPTOC, in contrast with the lack of such catalysis in the aminolysis of 4-nitrophenyl methyl carbonate, was explained by a smaller rate coefficient for expulsion of 4-nitrophenoxide (k2) which competes with amine deprotonation.
Keywords: Nucleophilic substitution, Thiocarbonyl center, Stepwise mechanism
Cite this paper: Shuchismita Dey, Prediction of Reaction Mechanism of Displacement Reactions at Thiocarbonyl Substrates, American Journal of Chemistry, Vol. 5 No. 2, 2015, pp. 55-59. doi: 10.5923/j.chemistry.20150502.02.
Article Outline
1. Introduction
- The nucleophilic displacement reactions at thiocarbonyl center have been considered in wide variety in organic Chemistry. Most of the reactions of this type proceed through stepwise mechanism. Stepwise mechanism includes formation of tetrahedral intermediate in the course of the reactions. The reaction mechanism explained based on, Brönsted constants in many cases. Other major tools such as Hammett Constants, Cross-interaction Constants have been used to clarify mechanism. This article includes an exclusive review on the mechanism of the nucleophilic reactions at thiocarbonyl centers considering research papers published by pioneering research groups of the World. Such as Castro et al. [5] reported that Kinetics and Mechanism of the Aminolysis of Phenyl and 4-Nitrophenyl Ethyl Thionocarbonates procceda reaction scheme with two hypothetical tetrahedral intermediates. Um et al. [11] reported, Effect of Amine Nature on Reaction Mechanism: Aminolyses of O-4-Nitrophenyl Thionobenzoate with Primary and Secondary Amines. Authors interpreted that, Pseudo-first-order rate constants (kobs) have been measured spectrophotometrically for reactions of O-4-nitrophenyl thionobenzoate with a series of primary and acyclic secondary amines. Most modern tools which have been used for mechanism studies have been explained initially in this review article so that readers can understand the content of the article very easily.
2. Tools for Mechanism Study
2.1. Free Energy Relationship [1]
- The mechanism of a chemical reaction can be interpreted using many techniques, among which the simplest, easiest, readily applicable, and the trickiest tool is the Free Energy Relationship. 8a Linear free energy relationships (LFER) are empirical observations which can be derived when the shapes of the potential energy surfaces (PES) of a reaction are not substantially altered by varying the substituent. 8a This type of correlation shows that the changes in structure produces proportional changes in the activation energy (∆G≠) and therefore known as linear free energy relationship. 8b In the early part of twentieth century the quantitative study of free energy relationship was introduced by the Danish scientist Johannes Nicolaus Brönsted (1923) and Swedish Scientist Louis Plack Hammett (1937). LFER can be classified into two categories. (i) Class I LFER: Compares a rate constant with the equilibrium of the same process. Brönsted equation is the example of this class of free energy correlation. (ii) Class II LFER: Compares a rate constant with the rate or equilibrium of an unconnected but similar process. The Hammett equation is the best known class II free energy relationship. Class II LFERs are in general more common than those of Class I, because equilibrium constants are more difficult to measure than rate measurement. LFER have been very useful in delineating the degree of nucleopilic participation, and the extent of leaving group bond fission, in the transition states of the reaction.
2.2. Hammett Equation [2]
- The Hammett equation (and its extended forms) has been one of the most widely used means for the study and interpretation of the organic reactions and mechanism. Hammett’s success is in treating the electronic effect of substituents on the rate of equilibria of organic reactions. The electronic effects of the substituents are composed of two main parts (i) a field/inductive component (ii) a resonance component. This electronic effect is governed by the substituent groups, which do not take part in there action but which are located near the reaction centers can perturb these strength. Two types of substituents are known (i) Electron donating group; enhance nucleophilic strength (basicity) and diminish electrophilic strength (acidity), (EDS; -CH, -NH, -OCH3etc.), (ii) Electron withdrawing group; enhance electrophilic strength (acidity) and diminish nucleophilic strength (basicity), (EWS; -NO2, -Cl, -Br, etc). The measured effects on rates are used to infer the electron-perturbing capabilities of the substituents. But for a certain period of time this contribution of substituents on reaction rates or equilibrium constants, in terms of the electronic effect, effectively consistent qualitatively. Hammett in 1937, quantified the effect of substituents on any reaction by defining an empirical electronic substituent, σ, derived from the acidity constants of meta (m) and para (p) substituted benzoic acids.Hammett equation can be expressed as follows.
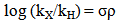 | (1) |
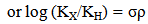 | (2) |
2.3. Brönsted Equation [3]
- Factors that govern the rates of chemical reactions have always been more difficult to understand and predict than those that govern their equilibria. Thus there has been a long standing interest in the empirical relationship between reaction rates and equilibria. The earliest example of a rate-equililibrium relationship is Brönsted catalysis law (1920 A.D.). Brönsted discovered that the rate constants of certain reactions that are catalyzed by acid/base are also dependent on the acid/base strength. For general acid or base catalysed reactions it is of importance to compare the activity of individual catalysts. Comparing a number of acids and bases it was found that the stronger the acid or the base, the greater the value of the specific catalytic constant. Since the acid acts as proton donor in aqueous medium, according to Arrhenius concept, when it catalyzes a reaction rate and when it reacts in an equilibrium reaction with the solvent, it seems logical to assume a parallel between the catalytic efficiency and the values of dissociation constants of the catalysts. Such deductions led Brönsted to derive a relationship between the values of specific rate constant and pKa values. A decade later it was shown that for a group of structurally related compounds a linear correlation between logarithms of rate and equilibrium constants can exists. This type of relationship is rather general and has been found for widely varying type of compounds in numerous types of reactions. Such relationship bears the general description of linear free energy relationship or extra thermodynamic relationships. A plot of the common logarithm of the reaction rate constant versus the logarithm of the ionization constant Ka for a series of acids (for example a group of substituted phenols or carboxylic acids) gives a straight line with slope α and intercept C. Brönsted equation is a free-energy relationship. The relationship implies that the Gibbs free energy for proton dissociation is proportional to the activation energy for the catalytic step. When the relationship is not linear, the chosen group of catalysts do not operate through the same reaction mechanism. Specific and general catalysis is also found in base catalysed reactions and base Brönsted equation also exists with constant β.
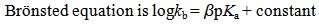 | (3) |
2.4. Cross-Interaction Constant Theory [4]
- Definition: Hammett and Brönsted equations establish LFER for one substituent have provided considerable insights into reactivity theory. The multiple substituents effect can also be analyzed quantitatively by extending these classical equations to include second derivative parameter, termed as Cross-interaction constants (CICs), shown in equations. The CICs, ρij (Hammett type constant) and βij (Brönsted type constant), represent the intensity of interaction between the two interacting molecules i (e.g., a nucleophile) and j (an electrophile) in the adduct which may be a TS, an intermediate or a product. It has become a very useful concept in the study of reaction mechanism by allowing more detailed prediction for the TS.
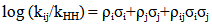 | (4) |
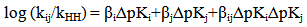 | (5) |
3. Reported Mechanism
- Castro et al. [5] reported that Kinetics and Mechanism of the Aminolysis of Phenyl and4-Nitrophenyl Ethyl Thionocarbonates procceda reaction scheme with two hypothetical tetrahedral intermediates: a zwitterionic (T±) and an anionic (T-) one, whereby amine catalysis (deprotonation intermediate kinetically important. Both the pKa of intermediates (and the rate coefficient for proton transfer (k3 ca. 1010 s-1 M-1) are estimated. The values of the other rate microcoefficients of the scheme are found by a nonlinear least-squares fitting, and these values are compared with those exhibited in the aminolysis of phenyl thionoacetate (PTOA), and S-phenyl and S-(4-nitrophenyl) O-ethyl dithiocarbonates (PDTC and NPDTC, respectively). The Brönsted type plots for amine basicity have slopes βN ca. 0.2 for rate-determining amine attack (k1) and βN ca. 0.8 for amine expulsion from T(k-1), in accord with the βN values found in similar aminolyses. The general base catalysis by amine found in the aminolysis of NPTOC, in contrast with the lack of such catalysis in the aminolysis of 4-nitrophenyl methyl carbonate, is explained by a smaller rate coefficient for expulsion of 4-nitrophenoxide (k2) from T(±) which competes with amine deprotonation of T(±) relative to the same expulsion from the analogous oxy intermediate.In a report, pioneer researchers of this field Castro et. al. [6] reported first time the kinetics of the aminolysis of thionocarbonates. In that work they carried out a kinetic and mechanisticstudy of the reactions of thionocarbonates with a series of secondary alicyclic amines in water. The aim was to compare these reactions with those of the same amines with phenyl thionoacetate and S-phenyl and S-(4-nitrophenyl) O-ethyl dithiocarbonates in water, in order to assess the influence of the nonleaving and leaving groups of the substrate on the kinetics and mechanism of these reactions. It was also of interest to examine the influence of the thiocarbonyl group by comparing the present reactions with those of similar oxycarbonates. The reactions of the substrates with secondary alicyclic amines were subjected to a kinetic study in aqueous solution at 25.0°C, ionic strength 0.2 M (KCl). Under amine excess, pseudo-first-order rate coefficients (kobsd) were found throughout. The order in amine was one for the reactions of piperidine but was of intermediate order between two compounds for the reactions of the other amines. The kinetic results can be accommodated by a reaction scheme with two hypothetical tetrahedral intermediates. The values of the other rate microcoefficients of the reactions were found by a nonlinear least-squares fitting, and these values were compared with those exhibited in the aminolysis of phenyl thionoacetate (PTOA), and S-phenyl and S-(4-nitrophenyl)O-ethyl dithiocarbonates (PDTC and NPDTC, respectively). The Brönsted type plots for amine basicity were rate-determining amine attack and for amine expulsion. The general base catalysis by amine found in the aminolysis of NPTOC, in contrast with the lack of such catalysis in the aminolysis of 4-nitrophenyl methyl carbonate, was explained by a smaller rate coefficient for expulsion of 4-nitrophenoxide (k2) which competes with amine deprotonation. These results were supported by other papers published in literature [7-10].In another report Um et al. [11] reported, Effect of Amine Nature on Reaction Mechanism: Aminolyses of O-4-Nitrophenyl Thionobenzoate with Primary and Secondary Amines. Authors interpreted that, Pseudo-first-order rate constants (kobs) have been measured spectrophotometrically for reactions of O-4-nitrophenyl thionobenzoate with a series of primary and acyclic secondary amines. The plots of kobs vs amine concentration are linear for the reaction of substrate with primary amines. The slope of the Brønsted-type plot for the reaction of substrate with primary amines decreases from 0.77 to 0.17 as the amine basicity increases, indicating that the reaction proceeds through a zwitterionic addition intermediate in which the rate-determining step changes from the breakdown of the intermediate to the reaction products to the formation of the intermediate as the amine basicity increases. On the other hand, for reactions with all the acyclic secondary amines studied, the plot of kobsvs amine concentration exhibits an upward curvature, suggesting that the reaction proceeds through two intermediates, e.g., a zwitterionic addition intermediate and an anionic intermediate. The microscopic rate constants (k1, k-1, k2, and k3 where available) have been determined for the reactions of substrate with all the primary and secondary amines studied. The k1 value is larger for the reaction with the primary amine than for the reaction with the isobasic acyclic secondary amines, while the k-1 value is much larger for the latter reaction than for the former reaction. The k3 value for the reaction with secondary amine is independent of the amine basicity. The small k2/k-1 ratio is proposed to be responsible for the deprotonation process observed in aminolyses of carbonyl or thiocarbonyl derivatives. To support these mechanism Um et. al. carried out more researches and published valuable articles from their research group. [12-15].To get further information from the research group of Castro et al. [16] reported that, The reactions of secondary alicyclic amines with the Phenyl and Methyl 4-Nitrophenyl Thionocarbonates are subjected to a kinetic study in aqueous solution, 25.0°C, ionic strength 0.2 (KCl), by following spectrophotometrically the release of 4-nitrophenoxide ion. Under amine excess, pseudo-first-order rate coefficients (kobsd) are found. For the reactions of phenyl 4-nitrophenyl thionocarbonate, linear plots of kobsdvs [NH] (NH is the free amine) are obtained, except for the reaction with piperazinium ion, which shows nonlinear upward plots. The aminolysis of methyl 4-nitrophenyl thionocarbonate exhibits nonlinear plots of kobsd vs [NH], except that with piperidine, which is linear. The Brönsted-type plot for reactant is linear with slope 0.25, indicating that the formation (k1 step) of a tetrahedral addition intermediate (T) is rate determining. For the aminolysis of 2 (except piperidine), k-1 _ k3 [NH] >k2, where k-1, k3, and k2 are the rate coefficients for amine expulsion, amine deprotonation, and leaving group expulsion from the intermediate, respectively. For the reaction of substrate with piperidine, k-1 <k3 [NH]; therefore, the k1 step is rate limiting. By comparison of the reactions under investigation among them and with similar aminolyses, the following conclusions can be drawn: (i) The change of MeO by EtO in 2 does not affect the k1, k-1, or k2 values. (ii) Substitution of MeO by PhO in results in lower k1 values due to steric hindrance. (iii) The change of 4-nitrophenoxy (NPO) by PhO in lowers the k1 values and enlarges those of k-1. (iv) Secondary alicyclic amines are less reactive toward than isobasic pyridines when the breakdown of T (is rate determining; this is mainly due to larger k-1 values for the former amines. (v) The change of PhO by NPO in one substrate changes the mechanism from stepwise to concerted. (vi) Substitution of NPO by PhO in one substrate does not alter the k1 values significantly. (vii) The change of NPO by Cl increases the k1 values. (viii) Substitution of CdS by CdO shifts the rate-limiting step from k1 to k2 due to a larger k-1/k2 ratio by this change.Lee et al. [17] reported that, Kinetic studies on the pyridinolysis of aryl furan-2-carbodithioates are carried out at 60.0°C in acetonitrile. The biphasic rate dependence on the pyridine basicity with a breakpoint at pKa° 5.2 is interpreted to indicate a change of the rate-limiting step from breakdown with slopes 0.7-0.8) to formation with slope 0.2 of the tetrahedral intermediate, at the breakpoint as the basicity of the pyridine nucleophile is increased. Observation of the breakpoint is possible with pyridines since the expulsion rate of the pyridine (k-a) from the intermediate is sufficiently low, with the low k-a/kb ratio leading to a low breakpoint, pKa°. The clear-cut change in the cross-interaction constants, ρXZ, from a positive +0.86) to a small negative -0.11 value at the breakpoint supports the mechanistic change proposed. The magnitudes of ρZ and activation parameters are also consistent with the proposed mechanism. Lee et al. supported these results by another published papers [18-20]. The most valuable parameters of their research group is Cross-interaction constant theory has applied to interpret the reaction mechanism [4, 21].Castro et al. [22] reported that The reactions of methyl 4-nitrophenyl, ethyl 4-nitrophenyl, and ethyl 2,4-dinitrophenyl thionocarbonates (MNPTOC, ENPTOC, and EDNPTOC, respectively) with a series of 3- and 4-substitutedpyridines are subjected to a kinetic investigation in water, 25.0°C, ionic strength 0.2 M (maintained with KCl). Under amine excess, pseudo-first-order rate coefficients (kobsd) are obtained, which are linearly proportional to the free-pyridine concentration. The second-order rate coefficients (kN) are obtained as the slopes of these plots. The Brönsted-type plots found for the two mono nitro derivatives coincide in one straight line (same slope and intercept) of slope 1.0. The EDNPTOC pyridinolysis shows a curved Brönsted-type plot with slopes 0.1 (high pKa), 1.0 (low pKa), and pKao) 6.8 (pKa value at the center of curvature). These plots are consistent with the existence of a zwitterionic tetrahedral intermediate on the reaction pathway whereby expulsion of aryloxide anion from T(is rate determining (k2 step) at low pKa for EDNPTOC (and in the whole pKa range for MNPTOC and ENPTOC), and there is a change to rate-limiting formation of T((k1step) at high pKa for EDNPTOC. Comparison of these Bronsted plots among them and with similarones permits the following conclusions: (i) There is no variation of kN by substitution of methoxy by ethoxy as the nonleaving group of the substrate. (ii) The pKao value is smaller for the less basic aryloxide nucleofuge due to a larger k2 value. (iii) The change of CdS by CdO as the electrophilic center of the substrate results in larger values for both k-1 (amine expulsion rate) and k2, and alsoa larger k-1/k2 ratio for the carbonyl derivative. There is also an increase of k1 by the same change. The K1k2 andk1k2/k-1 values are larger for the pyridinolysis of methyl 2,4-dinitrophenyl and methyl4-nitrophenyl carbonates compared to the corresponding thionocarbonates (EDNPTOC and MNPTOC, respectively). (iv) Pyridines are more reactive than isobasic secondary alicyclic amines toward ENPTOC when either the k1 step or the k2 step is rate limiting. This is explained by the softer nature of pyridines than alicyclic amines (k1 step) and the greater nucleofugality (k-1) of the latter amines than isobasic pyridines, leading to a larger k2/k-1 ratio for pyridines (k2 is little affected by the amine nature), and therefore a larger K1k2 value when the k2 step is rate determining). These results have been supported by other published articles from the same and other groups [23-30].
4. Conclusions
- The reaction between different amines and thiocarbonyl substrates in solution proceed through stepwise mechanism with tetrahedral intermediate in the course of the reactions. These are nucleophilic displacement type. Most common nucleophiles are different amines those have been used in different reactions. This conclusion was drawn in this review article based on important articles published by reputed and pioneering groups. The results have been considered are most recent and published in prestigious Journals with high impact factor.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML