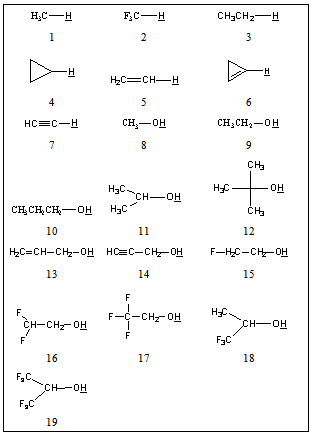
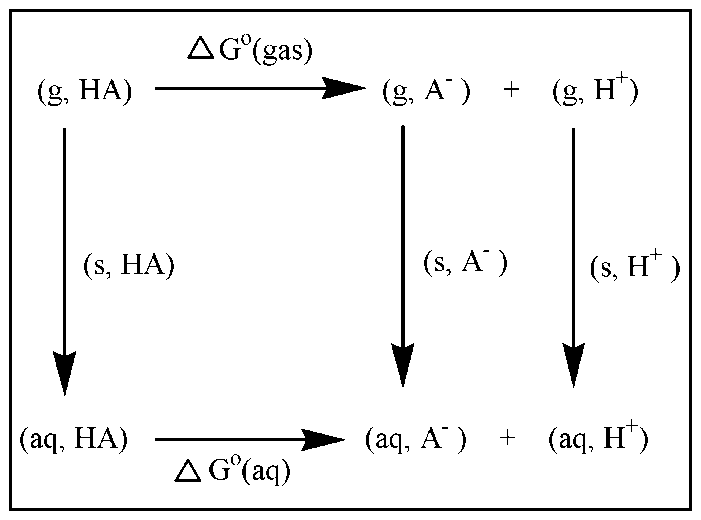
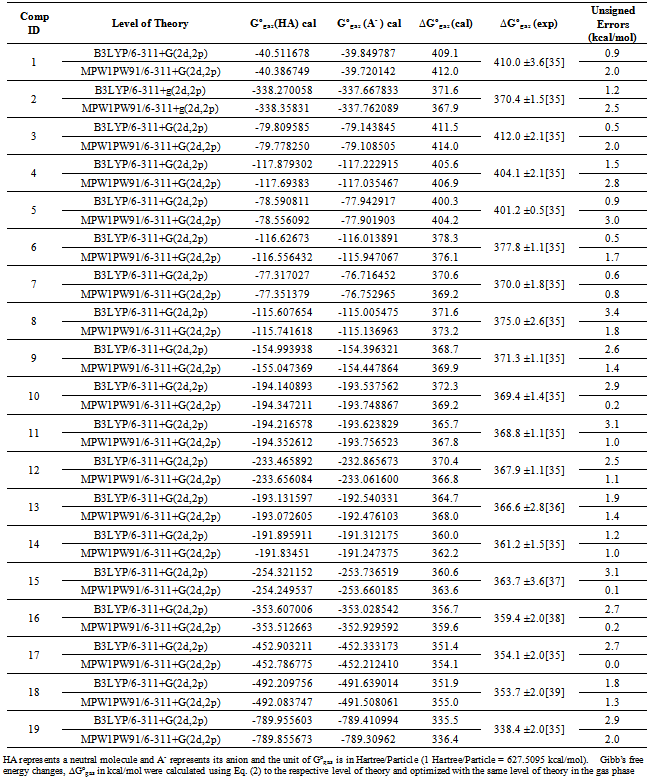
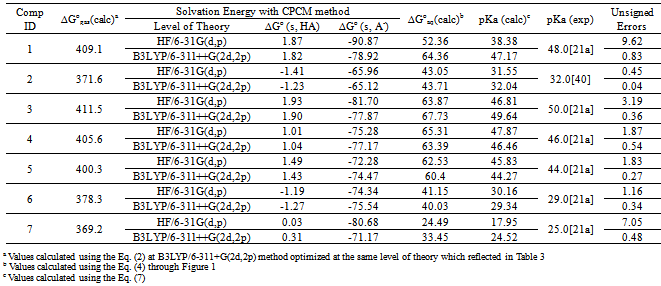
| [1] | Hansch, C., Sammes, P.G., Taylor, J.B., 1990, Comprehensive Medicinal Chemistry. Quantitative Drug Design, vol. 4, Pergamon Press, Oxford, UK. |
| [2] | Shuurmann, G., Markert, B., 1998, Ecotoxicology, Wiley, New York, p 665. |
| [3] | Smith, M.B. and March, J., 2007, March’s Advanced Organic Chemistry. 6th. edn., John Wiley, New York, pp 359–364. |
| [4] | Dewar, M.J.S. and Dieter, K.M., 1986, Evaluation of AM1 calculated proton affinities and deprotonation enthalpies., J. Am. Chem. Soc., 108, 8075-8086. |
| [5] | Siggel M.R., Thomas T.D., Saethre L.J., 1988, Ab initio calculation of Broensted acidities., J. Am. Chem. Soc., 110, 91-96. |
| [6] | Kass, S.R., 1990, Hydrocarbon acidities calculated with MINDO/3, MNDO, and AM., J. Comp. Chem., 11, 94-104. |
| [7] | Burk, P. and Koppel, I.A., 1993, Critical test of PM3 calculated gas-phase acidities., Theor. Chim. Acta., 86, 417-427. |
| [8] | Burk, P., Herodes, K., Koppel I., Koppel, I.A., 1993, Critical test of pm3-calculated proton affinities., Int. J. Quantum Chem., 27, 633-641. |
| [9] | Koppel, I.A., Taft, R.W., Anvia, F., Zhu, S.Z., Hu, L.Q., Sun, K.S., DesMarteau, D.D., Yagupolskii, L.M., Yagupolskii, Yu.L, Ignat’ev, N.V., Kondratenko, N.V., Volkonskii, A.Yu., Vlassov, V.M., Notario, R., Maria, P.C., 1994, The Gas-Phase Acidities of Very Strong Neutral Bronsted Acids., J. Am. Chem. Soc., 116, 3047-3057. |
| [10] | Burk, P., Koppel, I.A., Koppel, I., Yagupolskii, L.M., Taft, R.W., 1996, Super acidity of neutral Brönsted acids in gas phase., J. Comp. Chem., 17, 30-41. |
| [11] | Smith, B.J. and Radom, L., 1995, Calculation of Proton Affinities Using the G2(MP2,SVP) Procedure., J. Phys. Chem., 99, 6468-6471. |
| [12] | Smith, B.J. and Radom, L., 1995, Gas-phase acidities: a comparison of density functional, MP2, MP4, F4, G2(MP2, SVP), G2(MP2) and G2 procedures., J. Chem. Phys. Lett., 245, 123-128. |
| [13] | Liton, M.A.K., Ali, M.I., Hossain, M.T., 2012, Accurate pKa Calculations for Trimethylaminium ion with a variety of basis Sets and Methods Combined with CPCM Continuum Solvation Methods., Comp. Theor. Chem. (THEOCHEM), 999, 1-6 |
| [14] | Catalan, J. and Palomar, J., 1998, Gas-phase protolysis between a neutral Brønsted acid and a neutral Brønsted base., Chem. Phys. Lett., 293, 511-514. |
| [15] | Choho, K., Van Lier, G., Van de Woude, G., Geerlings, P., 1996, Acidity of hydrofullerenes: a quantum chemical study., J. Chem. Soc. Perkin. Trans., 2, 1723-1732. |
| [16] | Yang, W. and Mortier, W.J., 1986, The use of global and local molecular parameters for the analysis of the gas-phase basicity of amines., J. Am. Chem. Soc., 108, 5708-5711. |
| [17] | Contreras, R., Fuentealba, P., Galvan, M., Perez, P., 1999, A direct evaluation of regional Fukui functions in molecules., Chem. Phys. Lett., 304, 405-4011. |
| [18] | Perez, P., Simon-Manso, Y., Aizman, A., Fuentealba, P., Contreras, R., 2000, Empirical Energy−Density Relationships for the Analysis of Substituent Effects in Chemical Reactivity., J. Am. Chem. Soc., 122, 4756-4762. |
| [19] | Souza, F.D., Zandler, M.E., Deviprasad, G.R., Kutner, W., 2000, Acid−Base Properties of Fulleropyrrolidines: Experimental and Theoretical Investigations., J. Phys. Chem. A., 104, 6887-6893. |
| [20] | Rezende, M.C., 2001, A theoretical HSAB study of the acidity of carbon acids CH3Z. J. Braz., Chem. Soc., 12, 73-80. |
| [21] | (a) Alkorta, I. and Elguero, J., 1997, Carbon acidity and ring strain: A hybrid HF-DFT approach (Becke3LYP /6–311++G**)., Tetrahedron, 53, 9741-9744. (b) Rezende M.C., 2001, The acidity of carbon acids in aqueous solutions: correlations with theoretical descriptors., Tetrahedron, 57, 5923-5930. |
| [22] | Liptak, M.D., Gross, K.C., Seybold, P.G., Feldgus, S., Shields, G.C., 2002, Absolute pKa Determinations for Substituted Phenols., J. Am. Chem. Soc., 124, 6421-6427. |
| [23] | Charif, I.E., Mekelleche, S.M., Villemin, Mora-Diez, N., 2007, Correlation of aqueous pKa values of carbon acids with theoretical descriptors: A DFT study., THEOCHEM, 818, 1–6. |
| [24] | Lim, C., Bashford, D., Karplus, M., 1991, Absolute pKa calculations with continuum dielectric methods., J. Phys. Chem., 95, 5610-5620. |
| [25] | Liptak, M.D. and Shields, G.C., 2001, Accurate pKa Calculations for Carboxylic Acids Using Complete Basis Set and Gaussian-n Models Combined with CPCM Continuum Solvation Methods., J. Am. Chem. Soc., 123, 7314-7319. |
| [26] | Frisch, M.J. et al, 2003, GAUSSIAN 03, Revision B.05, Gaussian Inc., Pittsburgh, PA. |
| [27] | Cossi, M., Rega N., Scalmani, G., Barone, V.J., 2003, Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model., Comput. Chem., 24, 669-681. |
| [28] | Curtiss, L.A., Raghavachari, K., Redfern, P.C., Rassolov, V., Pople, J.A., 1998, Gaussian-3 (G3) theory for molecules containing first and second-row atoms., J. Chem. Phys., 109, 7764-7776. |
| [29] | Montgomery, J.A., Frisch, M.J., Ochterski, J.W., Petersson, G.A., 1999, A Complete Basis Set Model Chemistry. VI. Use of Density Functional Geometries and Frequencies., J. Chem. Phys., 110, 2822-2827. |
| [30] | Palascak, M.W. and Shields, G.C., 2004, Accurate experimental values for the free energies of hydration of H+, OH-, and H3O+., J. Phys. Chem. A, 108, 3692-3694. |
| [31] | Liptak, M.D. and Shields, G.C., 2001, Accurate pKa calculations for carboxylic acids using complete basis set and Gaussian-n models combined with CPCM continuum solvation methods., J. Am. Chem. Soc., 123, 7314–7319. |
| [32] | Kelly, C.P., Cramer, C.J., Truhlar, D.G., 2007, Single-ion solvation free energies and the normal hydrogen electrode potential in methanol, acetonitrile, and dimethyl sulfoxide., J. Phys. Chem. B, 111, 408-422. |
| [33] | Kelly, C.P., Cramer, C.J., Truhlar, D.G., 2006, Aqueous solvation free energies of ions and ion–water clusters based on an accurate value for the absolute aqueous solvation free energy of the proton., J. Phys. Chem. B, 110, 16066-16081. |
| [34] | Tissandier, M.D., Cowen, K.A., Feng, W.Y., Gundlach, E., Cohen, M.J., Earhart, A.D., Coe, J.V., 1998, The proton’s absolute aqueous enthalpy and Gibb’s free energy of solvation from cluster-ion solvation data., J. Phys. Chem. A, 102, 7787-7794 |
| [35] | Lias, S.G., Bartmess, J.E., Liebman, J.F., Holmes, J.L., Levin, RD, Mallard, W.G., 2010, Ion energetics data. In: NIST Chemistry WebBook, NIST Standard Reference Database Number 69, Eds. P.J. Linstrom and W.G. Mallard, National Institute of Standards and Technology, Gaithersburg MD, 20899, http://webbook.nist.gov. |
| [36] | Graul, S.T., Schnute ME, Squires, R.R., 1990, Gas-Phase Acidities of Carboxylic Acids and Alcohols from Collision-Induced Dissociation of Dimer Cluster Ions., Int. J. Mass. Spectrom. Ion. Proc., 96, 181-198. |
| [37] | Clair, R.L. and McMahon, T.B., 1980, An ion cyclotron resonance study of base-induced elimination reactions of fluorinated alcohols and unimolecular loss of HF from chemically activated fluoroalkoxide ions., Int. J. Mass. Spectrom. Ion. Phys., 33, 21-36. |
| [38] | Bartmess, J.E., Scott, J.A., McIver, R.T., Jr., 1979, Scale of acidities in the gas phase from methanol to phenol., J. Am. Chem. Soc., 10, 6046-6056. |
| [39] | Caldwell, G., McMahon, T.B., Kebarle, P., Bartmess, J.E., Kiplinger, J.P., 1985, Methyl substituent effects in the gas phase acidities of halosubstituted oxygen acids. A realignment with substituent effects in solution., J. Am. Chem. Soc., 107, 80-82. |
| [40] | Bordwell, F.G., 1988, Equilibrium acidities in dimethyl sulfoxide solution., Acc. Chem. Res., 21, 456–463. |
| [41] | Stewart, R., 1985, The Proton: Applications to Organic Chemistry Academic: New York. |
| [42] | Ballinger, P. and Long F.A., 1960, Acid Ionization Constants of Alcohols. II. Acidities of Some Substituted Methanols and Related Compounds., J. Am. Chem. Soc., 82, 795-798. |
| [43] | KIRK-OTHMER, 1994, Encyclopedia of Chemical Technology, 4th ed., 11, 521 |
| [44] | Ballinger, P. and Long, F.A., 1959, Acid Ionization Constants of Alcohols. I. Trifluoroethanol in the Solvents H2O and D2O1., J. Am. Chem. Soc., 81, 1050-1053. |


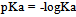
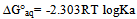
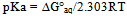
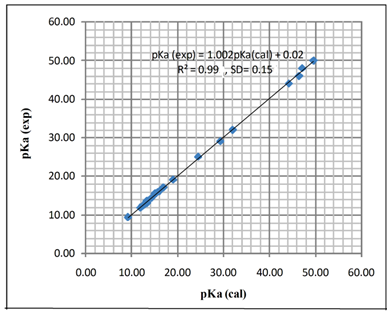
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML