Amina S. Al-Jaber1, Mohamed A-Z. Eltayeb2, Yousif Sulfab2, 3
1Department of Chemistry and Earth Sciences, College of Arts and Science, Qatar University, P. O. Box 2713, Doha, Qatar
2Chemistry Department, College of Science Technology, Alneelain University, Khartoum, Sudan
3Chemistry department, College of Science, University of Khartoum, Khartoum, Sudan
Correspondence to: Yousif Sulfab, Chemistry Department, College of Science Technology, Alneelain University, Khartoum, Sudan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The oxidation of [Fe(CN)6]4- by IO3- in the pH 1.62 -2.70 range is autocatalytic whether the reductant or oxidant is in excess. Typical first order plots of -ln(A∞ -At) versus time are curved showing an increase in rate with the progress of the reaction. It was possible, however, to obtain the pseudo first order rate constants (ku) for the uncatalyzed [Fe(CN)6]4--IO3- reaction from the linear parts of these plots. The linearity of the plots decreases with increasing concentrations of [Fe(CN)6]4-, IO3- and H+. The pseudo first order rate constant (kobs) for the whole reaction was obtained using ln[(At/A∞)/(1 - At/A∞)] versus time and/or a nonlinear curve fitting for sigmoidal reactions. The rate constant, kobs obtained by both methods varies with the initial concentration of [Fe(CN)6]4- according to Eqn. (i), where ku is the rate constant of the direct reaction between [Fe(CN)6]4- and IO3- and ka is the rate constant of the autocatalytic reaction. The values of ku, at different reactions conditions, obtained from plots of kobs vs [Fe(CN)64-]i are in fairly good agreement with values obtained from linear sections of first order plots.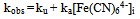 (i)Both ku and ka showed a first order dependence on [IO3-]. The dependence of ku on [H+] is complex as shown in Eqn. (ii). A polynomial fit of k2(1 + K1[H+]) vs [H+] has a zero intercept in agreement with Eqn. (iii)The catalytic rate constant varies with [H+] according to Eqn. (iii)
(i)Both ku and ka showed a first order dependence on [IO3-]. The dependence of ku on [H+] is complex as shown in Eqn. (ii). A polynomial fit of k2(1 + K1[H+]) vs [H+] has a zero intercept in agreement with Eqn. (iii)The catalytic rate constant varies with [H+] according to Eqn. (iii)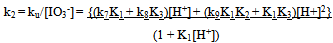 (ii)
(ii)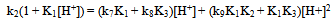 (iii)
(iii)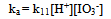 (iv)The overall dependence of kobs on [Fe(CN)64−], [IO3−] and [H+] is given by Eqn. (v).
(iv)The overall dependence of kobs on [Fe(CN)64−], [IO3−] and [H+] is given by Eqn. (v).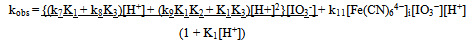 (v)At pH 4.33 no reaction between [Fe(CN)6]4− and IO3−was observed. When iodide is added to the reaction mixture at this pH, the reaction proceeded at measureable rate.
(v)At pH 4.33 no reaction between [Fe(CN)6]4− and IO3−was observed. When iodide is added to the reaction mixture at this pH, the reaction proceeded at measureable rate.
Keywords:
Hexacyanoferrate(II) , Iodate, Iodide, Kinetics, Autocatalytic Oxidation
1. Introduction
The kinetics of oxidation of [Fe(CN)6]4− by IO3− in the pH 1.77 – 2.65 range, under conditions where [Fe(CN)6]4− is in vast excess has been reported previously[1]. It was observed that the reaction is autocatalytic whether IO3- or [Fe(CN)6]4− is in vast excess. This is in agreement with an earlier report[2]. Nonetheless, rate constants were measured from the linear parts of pseudo first order plots with the reductant in vast excess over that of the oxidant. The closely related reaction between BrO3- and [Fe(CN)6]4− has also been reported and has shown a similar complexity[3,4]. The kinetics of this reaction in the relatively high [H+] (0.05 – 0.5 M) was found to be partially autocatalytic. Autocatalysis is believed to be caused by Br2 formed from the relatively fast reaction between Br− and BrO3− in the employed [H+] range[3]. The Br2 − [Fe(CN)6]4− reaction is shown to be very fast[3]. The kinetics of the BrO3− − [Fe(CN)6]4− reaction in the pH 3.6 – 5.8 range is also complex. The complexity of this reaction in this [H+] range, is claimed not to arise from the involvement of Br2, which is not formed in the BrO3- - Br- system at this pH range[4,5], but rather from the involvement of aquahexacaynoferrate(II) ([Fe(CN)5(H2O)]3−). Aquahexacaynoferrate(II) is formed very slowly in acidic solutions by replacing a CN- by an H2O and can be induced by light[6]. Deliberate addition of [Fe(CN)5(H2O)]3− has shown a remarkable effect on the BrO3- − [Fe(CN)6]4− reaction[4].Autocatalysis in IO3--[Fe (CN)6]4− reaction most likely arises from reaction between the product iodide and iodate in acidic solutions. The lower redox potential of I- facilitates its oxidation to I2 and/or I3− by IO3−[7,8] at the pH values employed. The effect of deliberately added I- on the IO3− -[Fe(CN)6]4− reaction has been reported[9]. It was found that added I− accelerates this reaction considerably and the rate of reaction increases with increasing [I−] even at pH values where the reaction does not take place in absence of iodide. It has known that I2 reacts very rapidly with [Fe(CN)6]4−[10]. In recent years there has been a lot of interest and research activity in oscillating reactions. The system IO3− − SO32− − [Fe(CN)6]4− is oscillatory. In these types of reactions it is important to know the rate constant of the likely processes. These are used to build models for oscillating reactions[11]. In this study we report the kinetics of both the uncatalized and the autocatalytic processes in the IO3− − [Fe(CN)6]4− reaction with iodate in large excess.
2. Experimental
All the chemicals were reagent grade and were used as received. Stock solutions, buffer (HSO4−/SO42−) and solutions of K4Fe(CN)6.3H2O were freshly prepared and used immediately as described earlier[1]. The absorption of the product [Fe(CN)6]3− was monitored at λmax 420 nm using a Perkin Elmer Model Lambda 25 or a Shimadzu 1800 UV/VIS absorption spectrophotometer both equipped with a thermostatted cell-holder. The absorbance-time traces were recorded on XY recorder. The pH of the reaction solutions was measured using an ELICO LI 120 pH meter. The kinetics of the reaction was investigated under constant reaction conditions with [IO3-] in vast excess over that of [(Fe(CN)6)4-]. Both reactants concentrations as well as the pH were varied.
3. Results and Discussions
The stoichiometry of the IO3--[Fe(CN)6]4− is well established and is given by Eqn.(1).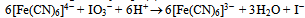 | (1) |
It was previously reported that the IO3−− [Fe(CN)6]4− reaction is autocatalytic[1,2]. The absorbance- time trace for the IO3− − [Fe(CN)6]4− reaction does not display the exponential growth of [Fe(CN)6]3− expected for a first order reaction. A similar behavior was observed in the [Fe(CN)6]4− − BrO3− reaction at relatively high [H+][3]. Plots of ln(A∞ -At) versus time, where A∞ and At are absorbance values at infinity and time t respectively, show marked deviation from linearity as shown in Fig. 1. The deviation from linearity of the plots depends on the initial concentrations of IO3−, [Fe(CN)6]4− and [H+]. The higher the concentration of the reactants, the shorter is the linearity of the plots. The first order rate constants for the uncatalyzed path, ku, were obtained from the linear parts of these plots. It was found that ku is fairly constant and does not depend on the initial concentration of [Fe(CN)6]]4− at fixed reaction conditions as shown in Table 1. The data of Fig. 1 is analyzed using a treatment for an autocatalytic reaction[12-14]. Plots of ln[(At/A∞)/(1 - At/A∞)] versus time are linear as shown in Fig. 2. This treatment was applied only in the range where autocatalysis becomes dominant. In the low pH range autocatalysis starts early and a nearly S-shaped form of absorbance-time curve is observed. The values of the slopes (kobs, s-1) obtained from Fig. 2 and similar plots are dependent on the initial concentration of [Fe(CN)6)4−]i. The absorbance-time data were also treated using a nonlinear curve fitting using an Origin 7.0 sigmoidal growth curve fitting program. A typical nonlinear fit for the data in Fig. 1 is shown in Figure 3. Values of kobs obtained using both methods are within 0- 8% variation. Most of kobs values were obtained using the non-linear curve fitting program.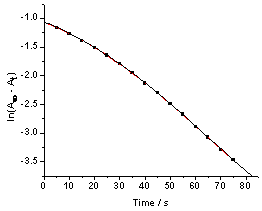 | Figure 1. First order plot of the IO3-- [Fe(CN)6]4- reaction, [IO3-] = 5.0 X 10-3 M, [Fe(CN)64-] = 5.4 x 10-4 M, pH = 1.53, I = 1.0 M and T = 25.0 ℃ |
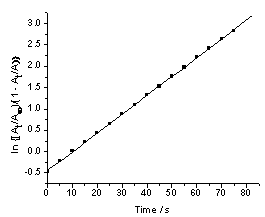 | Figure 2. Data in Fig. 1 plotted using ln[At/A∞)/(1 - At/A∞)] versus time |
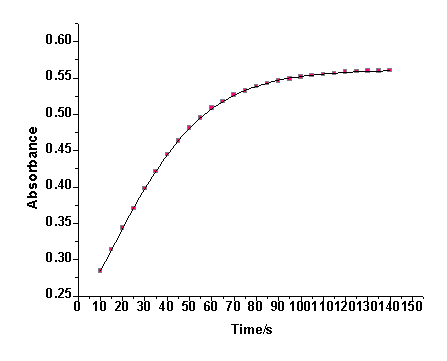 | Figure 3. Data in Fig. 1 plotted using Boltzmann sigmoidal growth for a non-linear curve fitting program |
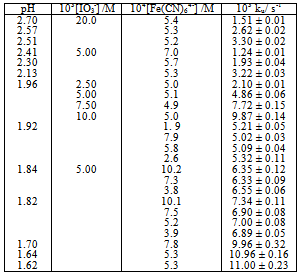
Table 1. Kinetic data for the for the uncatalyzed [Fe(CN)6 ]4- - IO3- reaction at 25.0 ℃, I = 1.0 M
 |
| |
|
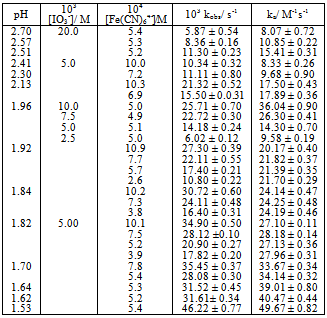
Table 2. Kinetic data for the catalyzed [Fe(CN)5]4- − IO3- reaction at 25.0 ℃, I = 1.0 M
 |
| |
|
The value of kobs varies with the [Fe(CN)6)4−]i, at fixed reaction conditions, according to Eqn. (2). The values of ku obtained from plots o Eq. (2) are in fairly good agreement with values obtained directly from linear portions of the first order plots. The rate constants ku and ka are rate constants for the uncatalyzed and the autocatalytic reactions pathways respectively. Values of ka were also calculated from Eqn. (2) using known values of kobs, ku and [Fe(CN)64−]i. 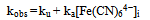 | (2) |
Table 1 shows that ku varies linearly with [IO3-] at fixed reaction conditions. The results in Table 1 also show that ku is pH-dependent. The dependence of kuc on [H+] seems to be complex as a plot of log ku versus log [H+] has a slope ≈1.3. The rate law for the uncatalyzed oxidation of [Fe(CN)6]4− by IO3− is given by Eqn. (3) at fixed pH, ionic strength and temperature. The form of this rate law is the same as that reported before[1].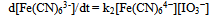 | (3) |
Hexacyanoferrate(II) is known to be extensively protonated in aqueous acidic solutions[15].The thermodynamic dissociation constants for the mono- and diprotonated species ([HFe(CN)6]3− and [H2Fe(CN)6]2− respectively) have been determined as 5.25 x 10-5 and 4.3 x 10-3 at 25 ℃ respectively. At 1.0 M ionic strength and 25 ℃ the values of the dissociation constants are 4.68 x 10-3 and 0.32 for the mono and diprotonated species respectively[16]. The iodate ion is appreciably protonated in aqueous acidic solutions and has a thermodynamic dissociation constant of 0.16 at 25 ℃[17]. The value of the dissociation constant at I = 1.0 M, and T = 25 ℃ is reported as 0.514 M[18].The major reaction steps for the uncatalyzed path are given by Eqns. 4 - 11. | (4) |
 | (5) |
 | (6) |
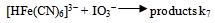 | (7) |
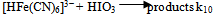 | (10) |
From the above equilibria and reactions the rate law in Eq. (10) is derived.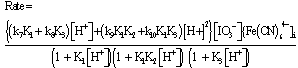 | (11) |
Since the reaction is first order in both [Fe(CN)64−]i and [IO3−] , the second order rate constant k2 (k2 = ku/[IO3−] varies with [H+] according to Eqn. (11).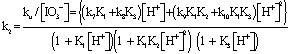 | (12) |
Under conditions where (1 + K1[H+]) >> (1 + K1K2[H+]2) (1 + K3[H+]), Eqn. (12) takes the form of Eqn. (13).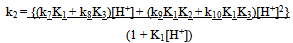 | (13) |
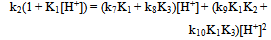 | (14) |
Eqn. (13) may be rearranged to the form of Eqn. (14). A polynomial of the second degree fit of a plot of k2(1 + K1[H+]) vs [H+] is shown in Fig. 4. From the polynomial fit (Fig.4) the value (k7K1 + k8K3) = (81.4 ± 17.2) and (k9K1K2 + k10K1K3) = (2.01 ± 0.07) x 104. These values are approximately twice as much as the previously determined values[1]. It was previously reported that the rate constant, contrary to expectation, decreases with increasing ionic strength. This may be rationalized by recalling that the protonation constants K1 and of [Fe(CN)6]4- (for the formation of [HFe(CN)6]3-, [H2Fe(CN)6]2- respectively) are lower at higher ionic strength values. Thus values of 1.49 x 104 M-1and 2.14 x 102 M-1 are reported for K1at infinite dilution and I = 1.0 M respectively[15,16]. | Figure 4. A second degree polynomial plot of k2(1 + K1[H+]) vs [H+], [IO3-] = 5.0 x10-3, I = 1.0 M, T = 25.0 ℃ |
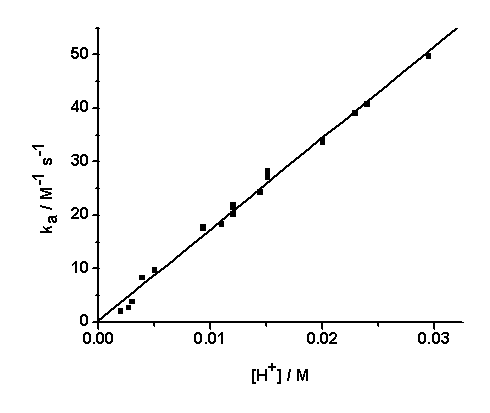 | Figure 5. Dependence of ka on [H+], [IO3-] = 5.0 x10-3/ M, I = 1.0/ M, T = 25.0 ℃ |
The dependence of kobs on [(Fe(CN)6)4−]i is indicative of the relationship between the concentration of the iodide product and the [(Fe(CN)6)4−]I; the higher the concentration of the latter, the higher would be the rate of formation of iodide. The iodide produced would react with IO3− according to Eqn.4 to generate iodine that would react rapidly with [(Fe(CN)6)]4- (Eqn. 5). Values of ka at several pH values are shown in Table 2 at constant [IO3−], ionic strength and temperature. The dependence of ka on [H+] (Fig. 5) shows a linear plot of ka versus [H+] with an almost zero intercept.The autocatalytic pathway is caused by a product generated by the uncatalyzed reaction. The I- produced in the direct reaction between [Fe(CN)6]4− and IO3− in acidic solutions (Eqn.1) reacts with IO3- to produce a more reactive species with [(Fe(CN)6)]4- than IO3- such as those in Eqn. (15).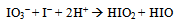 | (15) |
The reaction may also proceed to produce I2 which also reacts very rapidly with [Fe(CN)6]4− and this may cause autocatalysis in the [Fe(CN)6]4−− IO3− reaction[10]. The IO3−- I− reaction is thus the rate determining step and the catalyzed reaction is simply an indirect method for the measurement of the kinetics of this reaction under condition of low [I−]. The kinetics of the IO3−− I− reaction has been studied extensively and different forms of the rate law has been reported[19]. The most accepted rate law is the one showing first order dependence on [IO3−] and second order in both [I−] and [H+]. Results in Table 2 and Fig.5 show that ka varies linearly with [H+] and is described by Eqn. (16).In conclusion the iodate – hexacyanoferrate(II) reaction is partially autocatalytic whether the reductant or the oxidant is in excess. Autocatalysis becomes important at high reactant concentrations and low pH. Autocatalysis may be caused by I(III), I(I) and/or I2 that are produced during IO3− - I− reaction. At low reactants concentration and high pH autocatalysis only appears at late stages of the reaction. Qualitative experiments showed that the deliberate addition of I− speeds up the reaction and it proceeds at a measureable at pH values it would not usually take place.
Acknowledgements
Y. S would like to thank Professor Ahmed A. Abdel-Khalek of the Department of Chemistry, Cairo University, Beni-Suef Branch, Egypt, for his help with some kinetic runs and Professor J. F. Perez-Benito of the Department of Chemistry, University of Barcelona, Portugal for useful information.
References
| [1] | Sulfab, Y.; Elfaki, H. Can. J. Chem. 52, 2001 (1974) |
| [2] | Eggert, J.; Scharnow, B. Z. Elektrochem. 27, 455 (1921) |
| [3] | J. Birk, J; Kozub, S. G. Inorg. Chem. 12 (1973) 2460 |
| [4] | Rabai, Gy.; Epstein, I. R. Inorg. Chem. 28, 732 (1989) |
| [5] | Rabai, Gy.; Bazsa, Gy.; Beck, M. T. Int. J. Chem. Kinet. 13, 1277 (1981) |
| [6] | Gaspar, V.; Beck, M. T. Polyhedron 2, 38 (1983) |
| [7] | Dushman, S. J. Phys. Chem. 8, 453 (1904). |
| [8] | Schildcrout S. M.; Fortunato, F. A. J. Phys. Chem. 79, 31 (1975) |
| [9] | Rabai, G.; Kaminaga, A.; Hanazaki, I. J. Phys. Chem. 99, 9795 (1995) |
| [10] | Reynolds, W. L. J. Am. Chem. Soc., 80, 1830 (1958) |
| [11] | Gaspar, V.; Showalter, K. J. Phys. Chem. 94, 4973 (1990) |
| [12] | Angus-Dunne, S. J.; Irwin, J. A.; Burns, R. C.; Lawrance, G. A; Craig, D. C. J. Chem. Soc. Dalton Trans. 2717 (1993) |
| [13] | Nolan, A. L.; Burns, R. C.; Lawrance, G. A. J. Chem. Soc. Dalton Trans. 3065 (2002) |
| [14] | Dahal, M.; Lawrance, G. A. Inorganic Reaction Mechanism 5, 117 (2004) |
| [15] | Jordan, J.; Ewing, G. J. Inorg. Chem. 1, 587 (1962) |
| [16] | Lavison, S. A.; Marcus, R. A. J. Phys. Chem. 72, 358 (1968) |
| [17] | Pethybridge, A. D.; Prue, J. E. Trans. Faraday Soc. 63, 2019 (1967) |
| [18] | Ramette, R. W. J. Chem. Educ, 36, 191(1959) |
| [19] | Wilson, I. R. in “Comprehensive Chemical Kinetics”, C. H. Bamford and C. F. H.Tipper, Ed. Amsterdam, Vol. 6. (1972) |

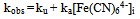 (i)Both ku and ka showed a first order dependence on [IO3-]. The dependence of ku on [H+] is complex as shown in Eqn. (ii). A polynomial fit of k2(1 + K1[H+]) vs [H+] has a zero intercept in agreement with Eqn. (iii)The catalytic rate constant varies with [H+] according to Eqn. (iii)
(i)Both ku and ka showed a first order dependence on [IO3-]. The dependence of ku on [H+] is complex as shown in Eqn. (ii). A polynomial fit of k2(1 + K1[H+]) vs [H+] has a zero intercept in agreement with Eqn. (iii)The catalytic rate constant varies with [H+] according to Eqn. (iii)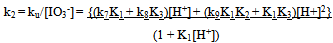 (ii)
(ii)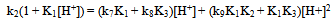 (iii)
(iii)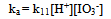 (iv)The overall dependence of kobs on [Fe(CN)64−], [IO3−] and [H+] is given by Eqn. (v).
(iv)The overall dependence of kobs on [Fe(CN)64−], [IO3−] and [H+] is given by Eqn. (v).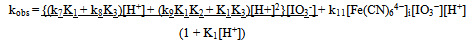 (v)At pH 4.33 no reaction between [Fe(CN)6]4− and IO3−was observed. When iodide is added to the reaction mixture at this pH, the reaction proceeded at measureable rate.
(v)At pH 4.33 no reaction between [Fe(CN)6]4− and IO3−was observed. When iodide is added to the reaction mixture at this pH, the reaction proceeded at measureable rate.
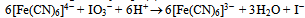



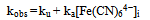
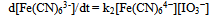



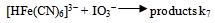
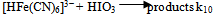
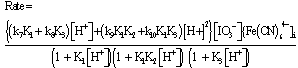
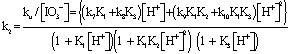
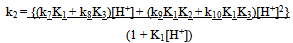
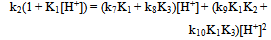


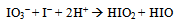
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML
