G. А. Pitsevich, А. E. Malevich
Belarusian State University, Independent Ave. 4, 220030 Minsk
Correspondence to: G. А. Pitsevich, Belarusian State University, Independent Ave. 4, 220030 Minsk.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The force field of a benzene molecule computed using the quantum-chemical GAMESS package with a set of independent vibrational coordinates in the approximation B3LYP/cc-pVTZ has been transformed to the set of redundant vibrational coordinates including all groups of the equivalent natural coordinates. It has been demonstrated that by the use of the transformed field all the initial frequencies of normal molecular vibrations may be found and the field symmetry may be recovered, with more adequate and clear forms of normal vibrations.
Keywords:
Force Fields, Vibrational Spectra, Sets of Redundant and Independent Vibrational Coordinates
Cite this paper: G. А. Pitsevich, А. E. Malevich, Recovery of Symmetry of Non-Empiric Force Fields of Cyclic Molecules in Going to Complete Sets of Equivalent Natural Coordinates, American Journal of Chemistry, Vol. 2 No. 1, 2012, pp. 24-27. doi: 10.5923/j.chemistry.20120201.06.
1. Introduction
Comparison between empiric and non-empiric molecular force fields, using of the latter in computations of normal molecular vibrations is of great interest in studies of various molecular properties. However, the empiric force fields have been derived, as a rule, for a redundant set of vibrational coordinates, whereas the non-empiric force fields are mostly computed with a set of independent vibrational coordinates. As in this case the researchers have to use incomplete sets of equivalent coordinates for the molecules of a particular symmetry, the computed values of the physically equivalent force constants are differing. It has been shown[1] that on definition of the rectangular matrix 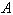 to express a set of the redundant natural coordinates
to express a set of the redundant natural coordinates 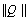 in terms of the independent set
in terms of the independent set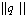 :
: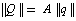 | (1) |
if we know the matrix of force constants K for a redundant set of vibrational coordinates, the matrix of force constants for a set of independent coordinates k may be found unambiguously as follows: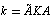 | (2) |
This has formed the basis for comparison between the empiric and non-empiric force fields. As shown by recent studies [2], if the pseudoinverse matrix 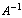 is found and for this matrix the following relations are true:
is found and for this matrix the following relations are true: 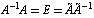 | (3) |
then in the case of a planar molecular fragment including three valence angles with a common vertex and one redundant coordinate the inverse transformation of a force field may be performed: 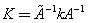 | (4) |
In this way a symmetry of the force field has been recovered for a molecule of ethylene.In[3] similar transformations were carried out for the molecules of methane and methanol including the regular and deformed tetrahedral fragments of six valence angles with a common vertex. It is well known that each of these fragments has a single redundant coordinate. As relation (3) is not true for all the rectangular matrices, the applicability of this approach to the molecules including other fragments with redundant coordinates should be checked directly in the process of computations. Apart from the molecular fragments considered in[2,3], redundant coordinates appear in cyclic molecules or in the molecules including the cyclic structures. Benzene is a typical representative of the first ones. Note that for molecules of methane and methanol a redundant set exceeds an independent set by a single coordinate, whereas for a molecule of benzene a redundant set of the vibrational coordinates exceeds an independent set by 24 coordinates. Because of this, it is rather difficult to find the matrix A. Moreover, a molecule of benzene includes the above-mentioned fragments of the first type involving the redundant coordinates.Computational method. Optimization of the geometry and computations of a force field for a benzene molecule have been performed using the quantum-chemical package GAMESS (VERSION = 1 OCT 2010 (R3))[4] in the approximation B3LYP/cc-pVTZ based on D6H symmetry. A set of independent coordinates included all valence coordinates, with the addition of deformation and torsional coordinates up to 3N–6. To find the matrix A, it is necessary to define a system of linear equations relating the redundant coordinates. As known[5], an addition of redundant coordinates leads to the appearance in the matrix of the kinematic coefficients G for new rows and columns forming linear combinations of the earlier ones. In the process the eigenvectors associated with zero eigenvalues of the matrix G constructed for the redundant coordinate set involve the same coefficients for the coordinates as should be in their linear combinations which are equal to zero. The matrix G for a molecule of С6Н6 has been computed using the geometry in Cartesian coordinates optimized with the help of[4] and the redundant set of 54 vibrational coordinates. Values for the elements of G matrix have been found with the use of the computational package for normal molecular vibrations[6]. Further automatization of the computations was realized using special software with Mathematica package[7]. The initial data are represented by the elements of G matrix computed for a redundant set of the coordinates, by the matrix elements of the force constants k computed with the help of[4] for the independent coordinates and converted to cm–2, and by lists of the coordinates in two sets. In this way the matrix G was diagonalized and the eigenvectors associated with its zero eigenvalues were found. Then a system of linear equations was derived to relate the redundant coordinates. As a result of solving this system, a redundant set of coordinates was expressed in terms of independent coordinates. On this basis the matrix A was generated and a form of the pseudoinverse matrix 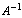 was found. Finally, with the use of relation (4), the matrix of force constants K was generated, whose elements were averaged in subsets of the equivalent sets. Keeping the geometry invariable, this force field was used as initial data in the package[6], and its adequacy was tested by comparison of the computed frequencies[6] for normal vibrations with the data given in[4].Force field of С6Н6 molecule. Fig.1 shows a molecule of benzene.
was found. Finally, with the use of relation (4), the matrix of force constants K was generated, whose elements were averaged in subsets of the equivalent sets. Keeping the geometry invariable, this force field was used as initial data in the package[6], and its adequacy was tested by comparison of the computed frequencies[6] for normal vibrations with the data given in[4].Force field of С6Н6 molecule. Fig.1 shows a molecule of benzene.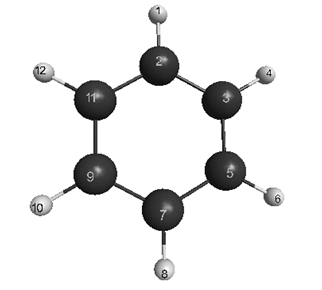 | Figure 1. Benzene molecule with numbering of atoms |
Let us consider the proposed approach in a greater detail taking plane coordinates of a benzene molecule as an example. 21 independent (qi) and 30 redundant (Qi) coordinates are introduced as follows: 
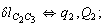
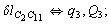

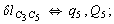
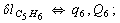
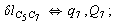
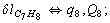

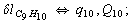
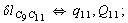
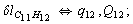
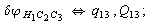
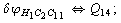
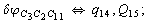

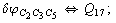
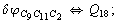
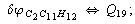
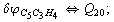
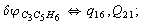
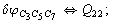
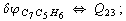

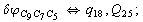
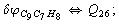
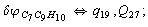
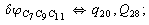
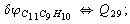
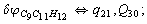 After diagonalization of the matrix for kinematic coefficients and after solving a system of linear equations, the redundant coordinate set is expressed in terms of independent coordinates and then the elements of the required matrix A are found. Some of the redundant coordinates may be expressed in terms of the independent ones in a fairly simple way, e.g., as:
After diagonalization of the matrix for kinematic coefficients and after solving a system of linear equations, the redundant coordinate set is expressed in terms of independent coordinates and then the elements of the required matrix A are found. Some of the redundant coordinates may be expressed in terms of the independent ones in a fairly simple way, e.g., as: 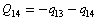 | (5) |
But involvement of the cycle results in a more complex system of linear equations. Because of this, the part of A matrix associated with the cycle formation takes the form: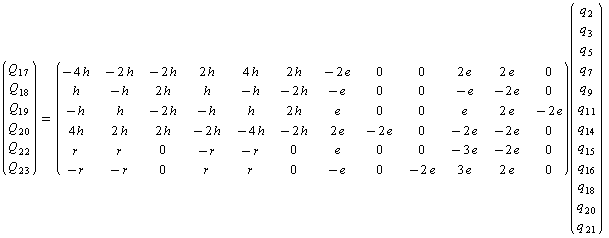 | (6) |
where h = 0.2267; r = 0.6802; e = 0.5. By relations of (6) the functions of some redundant coordinates are collectively performed by independent coordinates (up to nine). After finding of the pseudoinverse matrix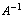 , the computations of the matrix K are performed and its elements are averaged within sets of the equivalent force constants. According to molecular symmetry for plane coordinates, 50 different sets of the equivalent force constants are formed, which include three, six or twelve elements. It is known[8] that with the use of 21 independent plane coordinates only 33 differing sets of the equivalent force constants are formed. Because of this, 50 force constants computed are not linearly independent. At the same time, they may be different by pairs. A force field for sets of independent and redundant non-plane coordinates, sets of the equivalent force constants for plane coordinates, the frequencies and normal modes of vibrations obtained using the fields for independent and redundant coordinates one can get from authors. Values of the force constants generating the equivalent sets for plane coordinates are listed in Table 1.
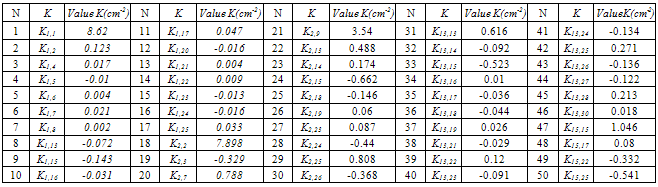
, the computations of the matrix K are performed and its elements are averaged within sets of the equivalent force constants. According to molecular symmetry for plane coordinates, 50 different sets of the equivalent force constants are formed, which include three, six or twelve elements. It is known[8] that with the use of 21 independent plane coordinates only 33 differing sets of the equivalent force constants are formed. Because of this, 50 force constants computed are not linearly independent. At the same time, they may be different by pairs. A force field for sets of independent and redundant non-plane coordinates, sets of the equivalent force constants for plane coordinates, the frequencies and normal modes of vibrations obtained using the fields for independent and redundant coordinates one can get from authors. Values of the force constants generating the equivalent sets for plane coordinates are listed in Table 1.Table 1. Values of the force constants generating the equivalent sets for plane coordinates
 |
| |
|
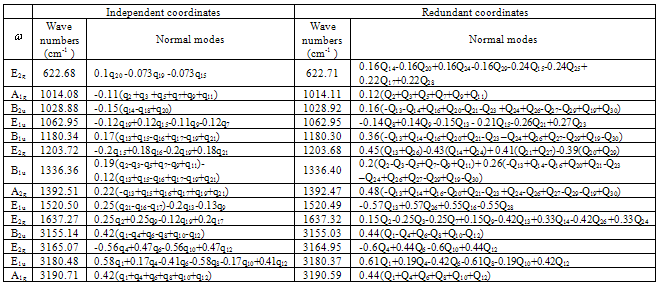
Table 2. Frequencies and normal modes of benzene plane vibrations
 |
| |
|
Despite the fact that a set of independent coordinates involves all valence С–С coordinates, the corresponding diagonal force constants are differing in their values. A minimal value of 11.146 cm–2 is obtained for 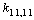 , and a maximal value of 13.860 cm–2 is associated with
, and a maximal value of 13.860 cm–2 is associated with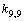 . The diagonal constant of the valence angle С–С–Н that is equal to 1.416 cm–2 is found to be the same for all the coordinates of this type. The corresponding constants for the three valence angles С–С–С involved in a set of the independent coordinates are different:
. The diagonal constant of the valence angle С–С–Н that is equal to 1.416 cm–2 is found to be the same for all the coordinates of this type. The corresponding constants for the three valence angles С–С–С involved in a set of the independent coordinates are different: 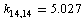 ;
; 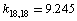 , and
, and 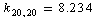 cm–2. After a change-over to a set of redundant coordinates, the field symmetry is recovered. Now the diagonal force constants for plane coordinates are as follows:
cm–2. After a change-over to a set of redundant coordinates, the field symmetry is recovered. Now the diagonal force constants for plane coordinates are as follows: 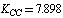 ;
; 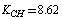 ;
; 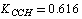 ;
; 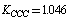 cm–2. Let us compare the values obtained with the empiric force constants. Several works are devoted to the derivation of a force field for a molecule of benzene[9-17]. The fundamental work by Wilson[9] presents the statement of the main principles for the construction of the generalized valence force field and the approach to apply the classical mechanics laws and group theory to molecular vibrations. The empiric force fields for a molecule of benzene are given in[10-17] with the use of symmetry coordinates and redundant natural coordinates. According to the results of[17],
cm–2. Let us compare the values obtained with the empiric force constants. Several works are devoted to the derivation of a force field for a molecule of benzene[9-17]. The fundamental work by Wilson[9] presents the statement of the main principles for the construction of the generalized valence force field and the approach to apply the classical mechanics laws and group theory to molecular vibrations. The empiric force fields for a molecule of benzene are given in[10-17] with the use of symmetry coordinates and redundant natural coordinates. According to the results of[17], 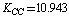 ;
; 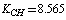 ;
; 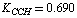 ;
; 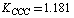 cm–2. As a whole, an agreement between the empiric and non-empiric diagonal force constants is fairly good. But the interaction force constants computed in the approximation B3LYP/cc-pVTZ in absolute value are, as a rule, higher than the corresponding empiric ones. As noted in[15,17], force interactions in a benzene ring are non-local in character. Indeed, rather high interaction force constants of the spatially-distant С–С bonds are selected in these works (e.g. 0.807 cm–2 for the opposite С–С bonds). According to our computational results, these interactions are considerably stronger than it has been presumed earlier; for the above-mentioned interaction, in particular,
cm–2. As a whole, an agreement between the empiric and non-empiric diagonal force constants is fairly good. But the interaction force constants computed in the approximation B3LYP/cc-pVTZ in absolute value are, as a rule, higher than the corresponding empiric ones. As noted in[15,17], force interactions in a benzene ring are non-local in character. Indeed, rather high interaction force constants of the spatially-distant С–С bonds are selected in these works (e.g. 0.807 cm–2 for the opposite С–С bonds). According to our computational results, these interactions are considerably stronger than it has been presumed earlier; for the above-mentioned interaction, in particular, 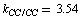 cm–2. It should be noted, however, that the force fields derived for a redundant set of coordinates are not unambiguously defined[5]. To illustrate, in[3] it has been stated that in the case of the regular tetrahedral fragment a simultaneous substitution of
cm–2. It should be noted, however, that the force fields derived for a redundant set of coordinates are not unambiguously defined[5]. To illustrate, in[3] it has been stated that in the case of the regular tetrahedral fragment a simultaneous substitution of 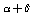 ,
, 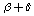 ,
, 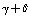 for the elements
for the elements 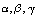 of the matrix K leaves the form of k matrix unaltered. Because of this, one should not expect that the empiric and non-empiric force fields transformed to a set of the redundant coordinates must be coincident. Next we consider a correlation between the frequencies and forms of normal plane vibrations in a benzene molecule for the force field given in Tab. 1 and the results of the initial non-empiric computation, see Tabl. 2.As seen, using the force field computed for a set of redundant coordinates one is enabled to reproduce in full the frequencies obtained in the initial quantum-chemical calculation.
of the matrix K leaves the form of k matrix unaltered. Because of this, one should not expect that the empiric and non-empiric force fields transformed to a set of the redundant coordinates must be coincident. Next we consider a correlation between the frequencies and forms of normal plane vibrations in a benzene molecule for the force field given in Tab. 1 and the results of the initial non-empiric computation, see Tabl. 2.As seen, using the force field computed for a set of redundant coordinates one is enabled to reproduce in full the frequencies obtained in the initial quantum-chemical calculation.
2. Conclusions
Thus, the force field of a benzene molecule computed by the non-empiric quantum-mechanical methods using a set of independent vibrational coordinates has been transformed to a set of redundant coordinates offering the possibility to recover a symmetry of the force field up to D6H. Invariability of the frequencies for normal molecular vibrations when using the transformed force fields provides support for the approach, especially because the forms of normal vibrations become more adequate and clear. Based on the previously noted[2,3] and observed in this work agreement between the non-empiric force constants for sets of redundant coordinates and the corresponding empiric force constants computed using the frequencies of the molecules under study and of their isotopic substituted derivatives, r.m.s. vibrational amplitudes, Coriolis constants, both approaches are adequate enough and efficient in computations of molecular force fields. The force constants, both scaled and non-scaled, transformed to a set of redundant coordinates may be easily extended to the related molecular fragments in large molecules with the help of the well-developed techniques for automated separation of force constants in standard program facilities used to compute normal vibrations[6].
References
| [1] | G.A. Pitsevich, I.P. Zyat’kov. J. Appl. Spectrosс., 58, Is. 1–2, (1993), 70. |
| [2] | G.A. Pitsevich, A.V. Kostopravova, D.S. Umreiko, M. A. Ksenofontov. J. Appl. Spectrosc. 78, Is. 5 (2011), 617. |
| [3] | G.A. Pitsevich. J. Spectrosc. Dyn. (2012), 2: 13 |
| [4] | http://www.msg.ameslab.gov/GAMESS/GAMESS.html |
| [5] | M.V. Vol’kenshtein, L.A.Gribov, M.A. El’yashevich, and B.I. Stepanov. Molecular Vibrations [in Russian], Nauka, Moscow (1972), p. 291. |
| [6] | V.V. Sivchik and K.M.Grushetskii. J. Appl. Spectrosс. 19, Is. 2, (1973), 317. |
| [7] | http://www.wolfram.com/mathematica/ |
| [8] | G.Varsanyi. Vibrational Spectra of Benzene Derivatives Akademiai Kiado, Budapest (1969), p.92. |
| [9] | E.B.Wilson. Phys. Rev. 45, (1934), 706. |
| [10] | B.C.Crawford, F.A. Mills. J.Chem.Phys., 17,(1949), 249. |
| [11] | M.A.Kovner. Dokl. Akad. Nauk SSSR, 91, (1953), 499. |
| [12] | D.H.Whiffen. Phil.Trans. Roy. Soc., A248, (1955), 131. |
| [13] | J.R.Scherer. Spectr. Acta, 21, (1965), 321. |
| [14] | N.Neto, M. Serocco, S. Califano. Spectr. Acta, 22, (1966), 1981. |
| [15] | J.C.Duinker, J.M. Mills. Spectr. Acta, 24A, (1968), 417. |
| [16] | E.C.O’Reilly. J.Chem.Phys., 51, (1969), 2207. |
| [17] | A.A.Ivlev, V.A. Dement’ev. J. Appl. Spectrosс., 20, Is. 2, (1974), 282. |

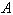 to express a set of the redundant natural coordinates
to express a set of the redundant natural coordinates 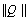 in terms of the independent set
in terms of the independent set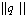 :
: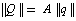
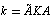
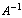 is found and for this matrix the following relations are true:
is found and for this matrix the following relations are true: 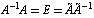
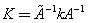
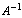 was found. Finally, with the use of relation (4), the matrix of force constants K was generated, whose elements were averaged in subsets of the equivalent sets. Keeping the geometry invariable, this force field was used as initial data in the package[6], and its adequacy was tested by comparison of the computed frequencies[6] for normal vibrations with the data given in[4].Force field of С6Н6 molecule. Fig.1 shows a molecule of benzene.
was found. Finally, with the use of relation (4), the matrix of force constants K was generated, whose elements were averaged in subsets of the equivalent sets. Keeping the geometry invariable, this force field was used as initial data in the package[6], and its adequacy was tested by comparison of the computed frequencies[6] for normal vibrations with the data given in[4].Force field of С6Н6 molecule. Fig.1 shows a molecule of benzene.

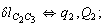
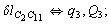

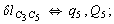
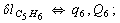
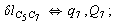
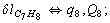

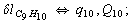
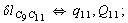
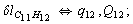
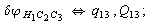
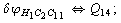
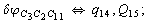

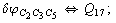
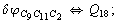
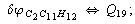
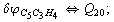
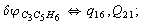
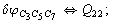
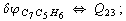

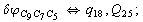
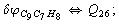
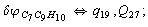
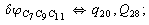
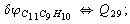
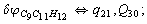 After diagonalization of the matrix for kinematic coefficients and after solving a system of linear equations, the redundant coordinate set is expressed in terms of independent coordinates and then the elements of the required matrix A are found. Some of the redundant coordinates may be expressed in terms of the independent ones in a fairly simple way, e.g., as:
After diagonalization of the matrix for kinematic coefficients and after solving a system of linear equations, the redundant coordinate set is expressed in terms of independent coordinates and then the elements of the required matrix A are found. Some of the redundant coordinates may be expressed in terms of the independent ones in a fairly simple way, e.g., as: 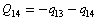
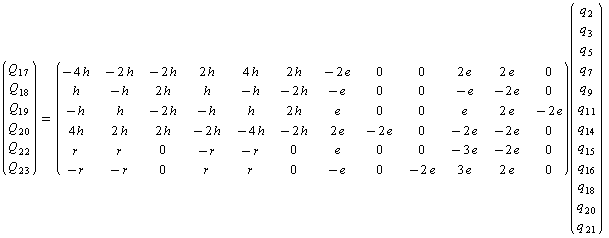
 , the computations of the matrix K are performed and its elements are averaged within sets of the equivalent force constants. According to molecular symmetry for plane coordinates, 50 different sets of the equivalent force constants are formed, which include three, six or twelve elements. It is known[8] that with the use of 21 independent plane coordinates only 33 differing sets of the equivalent force constants are formed. Because of this, 50 force constants computed are not linearly independent. At the same time, they may be different by pairs. A force field for sets of independent and redundant non-plane coordinates, sets of the equivalent force constants for plane coordinates, the frequencies and normal modes of vibrations obtained using the fields for independent and redundant coordinates one can get from authors. Values of the force constants generating the equivalent sets for plane coordinates are listed in Table 1.
, the computations of the matrix K are performed and its elements are averaged within sets of the equivalent force constants. According to molecular symmetry for plane coordinates, 50 different sets of the equivalent force constants are formed, which include three, six or twelve elements. It is known[8] that with the use of 21 independent plane coordinates only 33 differing sets of the equivalent force constants are formed. Because of this, 50 force constants computed are not linearly independent. At the same time, they may be different by pairs. A force field for sets of independent and redundant non-plane coordinates, sets of the equivalent force constants for plane coordinates, the frequencies and normal modes of vibrations obtained using the fields for independent and redundant coordinates one can get from authors. Values of the force constants generating the equivalent sets for plane coordinates are listed in Table 1. , and a maximal value of 13.860 cm–2 is associated with
, and a maximal value of 13.860 cm–2 is associated with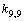 . The diagonal constant of the valence angle С–С–Н that is equal to 1.416 cm–2 is found to be the same for all the coordinates of this type. The corresponding constants for the three valence angles С–С–С involved in a set of the independent coordinates are different:
. The diagonal constant of the valence angle С–С–Н that is equal to 1.416 cm–2 is found to be the same for all the coordinates of this type. The corresponding constants for the three valence angles С–С–С involved in a set of the independent coordinates are different: 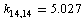 ;
; 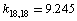 , and
, and 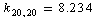 cm–2. After a change-over to a set of redundant coordinates, the field symmetry is recovered. Now the diagonal force constants for plane coordinates are as follows:
cm–2. After a change-over to a set of redundant coordinates, the field symmetry is recovered. Now the diagonal force constants for plane coordinates are as follows: 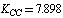 ;
; 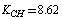 ;
; 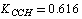 ;
; 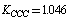 cm–2. Let us compare the values obtained with the empiric force constants. Several works are devoted to the derivation of a force field for a molecule of benzene[9-17]. The fundamental work by Wilson[9] presents the statement of the main principles for the construction of the generalized valence force field and the approach to apply the classical mechanics laws and group theory to molecular vibrations. The empiric force fields for a molecule of benzene are given in[10-17] with the use of symmetry coordinates and redundant natural coordinates. According to the results of[17],
cm–2. Let us compare the values obtained with the empiric force constants. Several works are devoted to the derivation of a force field for a molecule of benzene[9-17]. The fundamental work by Wilson[9] presents the statement of the main principles for the construction of the generalized valence force field and the approach to apply the classical mechanics laws and group theory to molecular vibrations. The empiric force fields for a molecule of benzene are given in[10-17] with the use of symmetry coordinates and redundant natural coordinates. According to the results of[17], 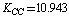 ;
; 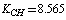 ;
; 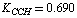 ;
; 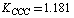 cm–2. As a whole, an agreement between the empiric and non-empiric diagonal force constants is fairly good. But the interaction force constants computed in the approximation B3LYP/cc-pVTZ in absolute value are, as a rule, higher than the corresponding empiric ones. As noted in[15,17], force interactions in a benzene ring are non-local in character. Indeed, rather high interaction force constants of the spatially-distant С–С bonds are selected in these works (e.g. 0.807 cm–2 for the opposite С–С bonds). According to our computational results, these interactions are considerably stronger than it has been presumed earlier; for the above-mentioned interaction, in particular,
cm–2. As a whole, an agreement between the empiric and non-empiric diagonal force constants is fairly good. But the interaction force constants computed in the approximation B3LYP/cc-pVTZ in absolute value are, as a rule, higher than the corresponding empiric ones. As noted in[15,17], force interactions in a benzene ring are non-local in character. Indeed, rather high interaction force constants of the spatially-distant С–С bonds are selected in these works (e.g. 0.807 cm–2 for the opposite С–С bonds). According to our computational results, these interactions are considerably stronger than it has been presumed earlier; for the above-mentioned interaction, in particular, 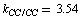 cm–2. It should be noted, however, that the force fields derived for a redundant set of coordinates are not unambiguously defined[5]. To illustrate, in[3] it has been stated that in the case of the regular tetrahedral fragment a simultaneous substitution of
cm–2. It should be noted, however, that the force fields derived for a redundant set of coordinates are not unambiguously defined[5]. To illustrate, in[3] it has been stated that in the case of the regular tetrahedral fragment a simultaneous substitution of 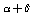 ,
, 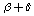 ,
, 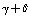 for the elements
for the elements 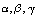 of the matrix K leaves the form of k matrix unaltered. Because of this, one should not expect that the empiric and non-empiric force fields transformed to a set of the redundant coordinates must be coincident. Next we consider a correlation between the frequencies and forms of normal plane vibrations in a benzene molecule for the force field given in Tab. 1 and the results of the initial non-empiric computation, see Tabl. 2.As seen, using the force field computed for a set of redundant coordinates one is enabled to reproduce in full the frequencies obtained in the initial quantum-chemical calculation.
of the matrix K leaves the form of k matrix unaltered. Because of this, one should not expect that the empiric and non-empiric force fields transformed to a set of the redundant coordinates must be coincident. Next we consider a correlation between the frequencies and forms of normal plane vibrations in a benzene molecule for the force field given in Tab. 1 and the results of the initial non-empiric computation, see Tabl. 2.As seen, using the force field computed for a set of redundant coordinates one is enabled to reproduce in full the frequencies obtained in the initial quantum-chemical calculation. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
