V. Jagannadham 1, R. Sanjeev 2
1Department of Chemistry, Osmania University, Hyderabad, 500007, India
2Department of Chemistry, Mizan-Tepi University, Tepi Campus, Tepi, Ethiopia
Correspondence to: V. Jagannadham , Department of Chemistry, Osmania University, Hyderabad, 500007, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Among the three states of matter the liquid state is tricky to be understood. The gas in an ideal approximation obeys the Maxwell-Boltzmann distribution. The solid if it is an ideal crystal follows the model of Einstein’s theory of heat capacity of solids. The properties of liquid lie in between those of gases and solids. The present article which is useful to senior under-graduate and graduate level students is focused to explain the properties of liquids by statistical thermodynamic approach. Using partition function approach from statistical thermodynamics and cell theory the physical meaning of liquid is well described in this article in terms of the communal entropy.
Keywords:
Liquid State, Partition Function, Entropy of Liquid, Communal Entropy, Cohesive Forces
Cite this paper:
V. Jagannadham , R. Sanjeev , "Is the Liquid a Condensed Gas or Collapsed Solid? A Statistical Thermodynamic and Cell Theory Approach: A Simple Introductory and Lucid One-Hour Class-Room Lecture for Physical Chemistry Senior Under-Graduate and Graduate Level Students", American Journal of Chemistry, Vol. 1 No. 2, 2011, pp. 26-28. doi: 10.5923/j.chemistry.20110102.05.
1. Introduction
In a dilute system of gaseous substance, the molecules are widely separated and move several angstroms before they "collide" with each other. In a solid, the molecules or atoms are fixed and the structure of solids and the distance between the molecules or atoms can be determined by x-ray diffraction. But the situation in liquids is quite different. The state in which a substance exhibits a characteristic ease to flow without dispersion and relatively high incompressibility is a liquid state. In a liquid, the packing is very similar to that of a solid except that the molecules are moving all the time in all directions with all velocities. In a liquid, there is also a definite structural arrangement in the vicinity of every particle and when we take an average over the structural arrangement of all the molecules, what we obtain is the structure of a liquid. The structure of liquids from X-diffraction in a lucid way at graduate students’ level is well documented[1]. The properties like (i) nature of cohesive forces, (ii) viscosity, (iii) surface tension, (iv) vapor pressure, (v) boiling point, (vi) freezing point, (vii) refractive index and (viii) optical rotation of some organic liquids with asymmetric centers aretaught at undergraduate level physical chemistry classroom, hence not discussed here.
2. Discussion
Liquids contain close packed aggregates of large number of molecules. This leads to liquids being much denser than their corresponding vapors and hence possesses definite volume. The inter-molecular forces are much stronger in liquids than the gases and yet they are not quite as strong as in solids. The molecules in liquids have kinetic energies similar to those in gases.Based on the cohesive forces, the structural units of liquid could be atoms as in Hg(l), could be molecules as in Br2(l) or H2O(l) and could be even ions as in molten NaCl, which exists as a liquid above 1100 K. As the temperature falls, the thermal motion of molecules in the gas phase decreases. If the temperature falls low enough, the thermal motion of the molecules is not great enough to overcome the attractive force between molecules, and the gas condenses to a liquid. However, the thermal motion in liquid still is great enough to prevent the molecules from assuming the ordered state characteristic of a crystalline solid. There is good deal of disorder in the liquid.As described by Henchman[2], figure 1 shows that a small group of molecules in one part of the liquid (Fig 1B) may have regular arrangement. But this regularity is not repeated throughout the liquid because the attractions between the molecules of the liquid are not great enough to create a completely ordered arrangement. The molecules in the gas (Fig. 1A) are in completely random motion. Where as the molecules in the solid (Fig. 1C) are highly ordered.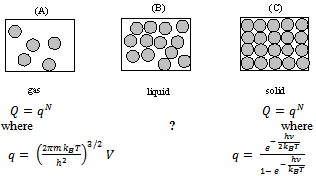 | Figure 1. Three main different states of matter: Fig. 1A is for a gas, 1B for a liquid and 1C is for solid |
It is important to note that one fundamental difference between molecules in the gas phase and the molecules in the liquid phase is the question of energy which is known as cohesive force (see later). Thermal energy is liberated when molecules in the gas phase form a liquid through their mutual attraction. Thermal energy must be added to overcome the attractions between molecules in the liquid phase to form the gaseous state. Similarly thermal energy is liberated when molecules in the liquid phase form a solid through their mutual attraction. Thermal energy must be added to overcome the attractions between molecules in the solid phase to form the liquid state.Real gases in an ideal approximation, at high temperature and low pressures are characterized by complete randomness. In an ideal gas, molecules move independently. The forces of attraction and repulsion are supposed to be absent. The total energy of an ideal gas is the simply the sum of the energies of the individual particles i.e. molecules. That is their internal energies plus the translational kinetic energy. And an ideal gas doesn’t have any intermolecular potential energy. Therefore one can write the translational partition function (assuming the absence of energies due to rotational and vibrational contributions, see the figure 1).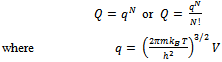 | (1) |
On the other hand the ideal crystal is Nature’s most orderly arrangement. And in an ideal crystal there are no translational and rotational kinetic energy contributions. In the ideal crystal the atoms or molecules or ions vibrate about their equilibrium positions. Therefore the kinetic energy contribution in an ideal crystal comes from its vibrational component. Therefore the partition function for vibrational contribution can be: see figure 1 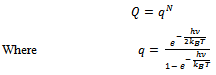 | (2) |
Because the two states of matter i.e. perfect chaos (gas) and perfect order (solid) are relatively simple to treat mathematically and it is possible to evaluate partition functions and hence several thermodynamic properties in both the cases. As pointed out above in the second paragraph in this section, the cohesive forces are strong enough to lead to a condensed state from gaseous state, but not strong enough to prevent a considerable translational energy of the individual molecules in liquid to become an ordered solid. Thermal motions introduce a disorder in to the liquid without completely destroying the regularity of its structure, it is therefore to evaluate a partition function for a liquid and hence the thermodynamic properties.Therefore the aim of the theory of liquids is to understand the transition between gas ⇌ liquid and liquid ⇌ solid and relate the thermodynamic properties, stability and structure of liquids to the size and shape of molecules and forces between them. Now at this juncture it is necessary to introduce the concept of entropy. Although somewhat abstruse, it is one of the fundamental concepts of physics and cryogenics. In studying the liquids it is better to recall the relation between entropy and degree of disorder. Crystal is always more favorable thermodynamically (or energetically) than liquid. When energy (Hf) is added to solid it melts. The equilibrium solid ⇌ liquid is governed by change in free energy at equilibrium (∆G = ∆H - T∆S). Randomness in liquid > solid hence liquid has greater entropy. Finally T∆S term is large enough to overcome the term ∆H. Therefore the condition for solid to melt is T(Sliq – Scry) = (Hliq – Hcry). Therefore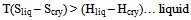 | (3) |
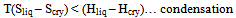 | (4) |
3. Cohesion of Liquids
3.1. Internal Pressure and its Significance
For a liquid state model the cohesive forces are also important. Ignoring the origin of these forces one can obtain an estimate of the magnitude from thermodynamic considerations in terms of internal pressure. It is known from thermodynamics that 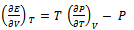 | (5) |
This is the thermodynamic equation of state since it contains P, V, T and E. The quantity 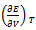 is internal pressure. And the quantity
is internal pressure. And the quantity 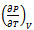 is thermal pressure. In the case of an ideal gas the internal pressure term
is thermal pressure. In the case of an ideal gas the internal pressure term 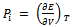 is zero since intermolecular forces are absent. But for non-ideal gas (or real gas) it becomes appreciable and in the case of a liquid it may even become much greater than Pext. Here Pi is the resultant of forces of attraction and forces of repulsion between the molecules in a liquid. Therefore it depends on the volume and thus on the external pressure.
is zero since intermolecular forces are absent. But for non-ideal gas (or real gas) it becomes appreciable and in the case of a liquid it may even become much greater than Pext. Here Pi is the resultant of forces of attraction and forces of repulsion between the molecules in a liquid. Therefore it depends on the volume and thus on the external pressure.
4. Partition Function Method Approach and the Cell Theory
For non-interacting particles the partition function is: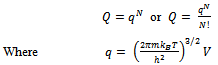 | (6) |
Here q is partition function of a single molecule in a volume of V which is potential free. In the cell theory one can imagine the volume V is divided up in to a lattice of N cells and one molecule in each cell. The molecule in the cell is independent of the other is similar to the situation to the treatment of Einstein equation of heat capacities of solids for mono atomic crystals. But in gases the molecules are free to wander in the volume of V due to which molecules possess additional entropy known as “Communal Entropy” not possessed by the molecules in a crystal. But the situation in liquids is in between and therefore the liquid contains some communal entropy to some extent if not as in the case of an ideal gas but certainly more than that in the perfect crystal. Now one can suppose N mono atomic molecules with no intermolecular forces in a volume of V, one can evaluate partition function (Q), Helmoltz free energy (A) and entropy (S).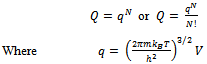 | (7) |
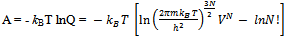 | (8) |
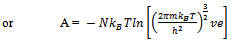 | (9) |
Where 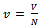 , volume of each cell in which a molecule moves inside and
, volume of each cell in which a molecule moves inside and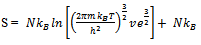 | (10) |
If the molecules resemble like particles in an Einstein crystal, they are supposed to be distinguishable then 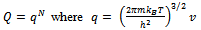 | (11) |
Therefore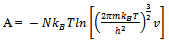 | (12) |
and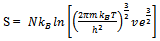 | (13) |
From equations 10 and 13 it is clear that if we start with system of particles and remove the partition the difference in entropy is “NkB” is due to wandering of molecules in V is called “Communal Entropy”.
5. Conclusions
For any phase diagram there will be a coexistence curve above that one can not distinguish a fluid is a gas or a liquid. The difference in liquid and gas is essentially a difference in the density. Therefore a liquid could be regarded as a dense gas. And similarly the difference in liquid and solid is essentially a difference again in the density. Therefore a liquid could be regarded as a collapsed solid. The theory of dense gas or collapsed solid is only exact away from the critical point and it breaks down when the liquid is present in the system.
References
| [1] | K. R. Rao, The Liquid State in: Resonance, Journal of Science Education, Published by Indian Academy of Sciences, Bangalore, India, vol. 2, number 6, page 54-59, 1997 |
| [2] | (a) Richard H. Henchman, The liquid state partition function in: New Directions in Liquid State Theory, July 2, 2007 to July 4, 2007, Location: CECAM 46 allée d’Italie 69007 Lyon France, (b) Richard H. Henchman, Partition function for a simple liquid using cell theory parameterized by computer simulation in: Journal of Chemical Physics, Vol. 119, page 400-406, 2003 (c) Richard H. Henchman, Free energy of liquid water from a computer simulation via cell theory in: Journal of Chemical Physics, 126, 64504, 2007 |
| [3] | Walter J. Moore, The liquid state in: Physical Chemistry, Orient Longmans Limited, Indian 4th Edition, New Delhi, page 703-723, 1969 |
| [4] | M. C. Gupta, The liquid state in: Statistical Thermodynamics, New Age International, New Delhi, page 338-356, 2007 |
| [5] | Peter Atkins and Julio de Pauelo, Elements of Physical Chemistry; page: 571; Fourth Indian Edition; Oxford Univ. Press; ISBN-13: 978-0-19-567252-7 |
| [6] | Thomas Engel and Philip Reid, Physical Chemistry, Low Priced Pearson Education Edition Licensed from Dorling Kindersely (India) Pvt., Ltd., 2006 |


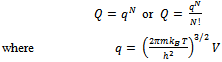
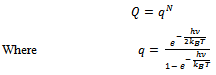
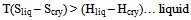
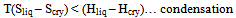
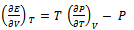
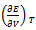 is internal pressure. And the quantity
is internal pressure. And the quantity 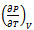 is thermal pressure. In the case of an ideal gas the internal pressure term
is thermal pressure. In the case of an ideal gas the internal pressure term 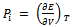 is zero since intermolecular forces are absent. But for non-ideal gas (or real gas) it becomes appreciable and in the case of a liquid it may even become much greater than Pext. Here Pi is the resultant of forces of attraction and forces of repulsion between the molecules in a liquid. Therefore it depends on the volume and thus on the external pressure.
is zero since intermolecular forces are absent. But for non-ideal gas (or real gas) it becomes appreciable and in the case of a liquid it may even become much greater than Pext. Here Pi is the resultant of forces of attraction and forces of repulsion between the molecules in a liquid. Therefore it depends on the volume and thus on the external pressure.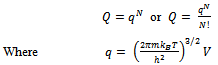
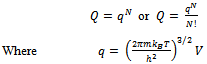
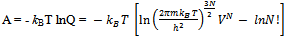
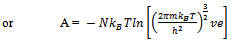
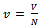 , volume of each cell in which a molecule moves inside and
, volume of each cell in which a molecule moves inside and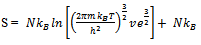
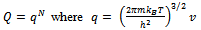
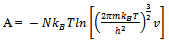
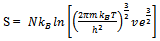
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML