-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Biophysics
p-ISSN: 2168-4979 e-ISSN: 2168-4987
2020; 10(1): 17-24
doi:10.5923/j.biophysics.20201001.03
Received: July 1, 2020; Accepted: July 27, 2020; Published: August 29, 2020

Effects of External Electric Field on the Thermodynamic Properties of Microtubules During Dynamic Instability
W. A. Nganfo, C. Kenfack-Sadem, M. C. Ekosso, S. N. Wopunghwo, M. F. C. Fobasso, A. J. Fotué, L. C. Fai
Condensed Matter and Nanomaterials, Faculty of Science, Department of Physics, University of Dschang, Cameroon
Correspondence to: C. Kenfack-Sadem, Condensed Matter and Nanomaterials, Faculty of Science, Department of Physics, University of Dschang, Cameroon.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

We investigate the dynamics of microtubules (MTs) under the influence of the electric field using the Ising model. The mean-field theory is used to compute the thermodynamic properties of the model such as polarization, critical temperature, and free energy in the absence and presence of the external electric field. The results show that the magnitude of the external electric field plays a critical role in symmetry breaking in MTs. However, when the magnitude of the external electric field is weak and the environmental temperature is below the critical value, the system adopts a favorable configuration where the transmission process occurs.
Keywords: Microtubules, Thermodynamic properties, Electric field, Mean-field theory, Symmetry breaking, The electric field
Cite this paper: W. A. Nganfo, C. Kenfack-Sadem, M. C. Ekosso, S. N. Wopunghwo, M. F. C. Fobasso, A. J. Fotué, L. C. Fai, Effects of External Electric Field on the Thermodynamic Properties of Microtubules During Dynamic Instability, International Journal of Biophysics , Vol. 10 No. 1, 2020, pp. 17-24. doi: 10.5923/j.biophysics.20201001.03.
Article Outline
1. Introduction
- Electronic microscopy imaging shows three major types of constituents in the cytoskeleton such as microtubules (MTs) [1,2], intermediate filaments, and actin microfilaments. Microtubules, major elements of the cytoskeleton are responsible for maintaining the shape of the cell, supposed to be the center of cellular organization and information processing. In fact, they play an important role in intracellular transport where they serve as road-rail for motors proteins, essential during cell division and cell motility [3,4,5]. X-ray crystallography shows that an MT is a hollow cylindrical tube about 25 nm in outer diameter and 14 nm in inner diameter [6,7,8]. The interior of the cylinder is likely to be filled with ordered water, which implies the existence of electric dipoles and an electric field. In fact, MT wall is an assembly of 13 protofilaments, each of which may be a series of subunit proteins referred to as tubulin dimers [9,10,11], capable of bonding GTP (guanosine triphosphate), but GTP bonded to β tubulin is a smaller amount stable than GTP bonded to α tubulin. After incorporating the dimer on the protofilament, β tubulin will hydrolyze its GTP to GDP (guanosine diphosphate). The hydrolyzed GDP will detach from the microtubule and therefore the latter is going to be liable for the dynamic instability. The dynamic instability of the MT is that the transition between the polymerization and depolymerization processes. The dynamic instability phenomenon was highly investigated during these last decades because its understanding reveals peculiar processes within cells. In 2013, Xin Li et al. [12], investigated a theoretical model of microtubule dynamics supported discrete-state stochastic models to elucidate the MTs dynamics accounting hydrolysis rate of GTP. They reported that the strong cooperatively in hydrolysis suppress dynamic instability while weak cooperatively in hydrolysis care the dynamics instability. Consistent with the role of MTs during chromosomes spindle Schwietert et al. [13], recently reported that cooperative stochastic microtubule depolymerization bistable force-velocity exhibited stochastic chromosome oscillations with reduced amplitude and a phase shift between sisters kinetochore. As MTs are road-rail for motor cargoes, Swaminathan et al. [14], in 2011, studied MTs self-organization by modeling MTs as polar rods and shown that originally disordered systems of interacting rods exhibit an orientational instability leading to spontaneous ordering. In fact, the tubulins dimers consist to β tubulin, positively charged, and α tubulin, negatively charged. These two tubulins form an electric dipole where the electron can be localized in α or β tubulin. Therefore the electric dipole is considered as a pseudo spin where the electron can be in spin-up or spin-down [15,16]. In that way, microtubule is ferroelectric, which is a characteristic of certain materials to have a spontaneous electric polarization that can be reversed by the application of an external electric field [17,18,19]. Many works on ferroelectric systems have been carried out using the Ising model in which collective effects are produced by local interactions between two-state particles [20-26] particularly microtubules because, of their intrinsic properties and by the way that they obey to collective interactions [11,27,28].The piezoelectric properties of the microtubule were first discovered by Athenstadt et al. [29], He was looking for piezoelectric effects in living systems. The measurement of its piezoelectric properties and the subsequent classification as a piezoelectric polymer declared the existence of a permanent electric dipole on the microtubule. In 1999, Brown et al. [30], re-examined the ferroelectric model of microtubules by showing the condition that the ferroelectric properties are important for the microtubule dynamics, and that microtubule can be affected by the transient endogenous electric fields of living cells. Pokorny et al. [31] 2004, showed that the vibrations produced in the cell can generate an external electric field that influences certain proteins of the cell such as microtubules. In 2011, Cifra et al. [32], measured the electric field generated by the modes of longitudinal vibration of axial microtubules in the dynamics. In 2017, Satelice et al. [33], showed that electrolytic solutions containing microtubules are small signal alternating current conductors. Also, the microtubules in an electrolyte diluted 20 times increase the conductance of the solution by 23% at 100 kHz. From the abovementioned, it is clear that the external electric field plays a significant role in MT dynamics. But, in 2004, Chen Ying et al. [11], approach MTs as a one-dimensional ferroelectric system and described the nonlinear dynamics of electric dipoles of dimers in a protofilament of the microtubule by virtue of the double-well potential, where they study MTs in the absence of the external electric field. They showed that the ferroelectric (FE) to paraelectric (PE) transition in the system occurs through temperature. Thus, we propose to give a theoretical look at external electric field effects on the ferroelectric character of MT dimers. In fact, in the ferroelectric phase, MT network orders their electrical dipoles in the same direction and allows efficient transportation of materials along with the network. While, in the paraelectric phase, electric dipoles are in disorder state where dimers are disorganized and the transport along the network is disturbed. These two phases are described by an order parameter which is polarization. The system is in the ferroelectric or ordered state when the polarization is different to zero and go to paraelectric state or disorder when the polarization is canceled, at a particular temperature usually call critical temperature or Curie Weiss temperature [34]. In this study, we aim to study the external electric field effects on MT’s properties using the mean-field theory (MFT) in order to bring a theoretical clear explanation of how to control the dynamical critical temperature and the information direction. The paper is organized as follows: section 2 describes MT’s system in terms of Hamiltonian and presents the mean-field approximation. Section 3 derives thermodynamic parameters and section 4 concludes.
2. Model and the Hamiltonian of the System
2.1. Model
- In the present paper, we assume that MT consisting of a nonlinear ferroelectric [10] chain of N sites of pseudo-spin capable to undergo various phases transitions. The total energy of MT ferroelectric chain can be more powerful describe by the Ising model. The Hamiltonian of the system is given by:
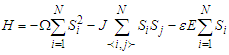 | (1) |
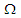 is the anisotropic coefficient [35,36],
is the anisotropic coefficient [35,36], 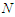 is the total number of tubulin dimers.
is the total number of tubulin dimers. 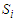 And
And 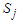 represents the pseudo-spin respectively in site i and site j with
represents the pseudo-spin respectively in site i and site j with 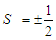 . The second term characterizes the nearest-neighbor exchange interaction energy between the spin of site i and the spin of site j, with an interaction coupling
. The second term characterizes the nearest-neighbor exchange interaction energy between the spin of site i and the spin of site j, with an interaction coupling 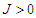 . The notation
. The notation 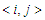 stands to the sum restricted to nearest-neighbor pair of pseudo-spin, each pair being counted only once [37]. The last term represents electric energy since
stands to the sum restricted to nearest-neighbor pair of pseudo-spin, each pair being counted only once [37]. The last term represents electric energy since 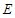 an external electric field and
an external electric field and 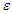 denotes the electric dipole moment. Let’s find the effective Hamiltonian of the system using mean-field theory (MFT) in order to derive MT’s properties.
denotes the electric dipole moment. Let’s find the effective Hamiltonian of the system using mean-field theory (MFT) in order to derive MT’s properties. 2.2. Effective Hamiltonian of the System and Mean-field Theory
- MT is a many-body system consisting of a chain of N sites of pseudo-spin. Therefore, it is complicated to explore the general behavior of the system without approximation. Thus, in order to simplify the system, certain aspects can be neglect. Many works on the Ising model use the mean-field theory (MFT) which assumes that thermal fluctuations are relatively small and therefore can be neglected. We assume that all tubulins in the system represented by a spin only interact with the mean-field, supposing that the effect of interaction between tubulins are considered weak and can be neglect during the approximation. Then the behavior of the whole system is captured by the average behavior of spin around [38]. To decouple the Ising Hamiltonian using MFT, let’s express the interaction terms
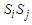 in the form:
in the form: 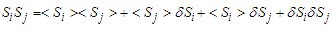 | (2) |
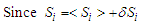 | (3) |
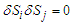 | (4) |
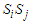 become:
become: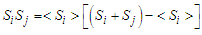 | (5) |
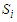 of any given site is independent of the site, so we can, therefore, weigh the average total spin by a specific number seen as order parameter which best describe, MT’s system. Then polarization is powerful to describe the whole behavior of the system:
of any given site is independent of the site, so we can, therefore, weigh the average total spin by a specific number seen as order parameter which best describe, MT’s system. Then polarization is powerful to describe the whole behavior of the system: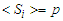 | (6) |
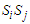 as:
as: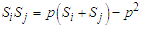 | (7) |
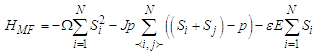 | (8) |
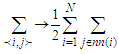 | (9) |
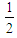 is to avoid double counting pairs of sites and
is to avoid double counting pairs of sites and 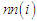 denotes nearest neighbors of
denotes nearest neighbors of 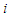 . Since there is no explicit j dependence inside the summation, this inner sum is simply and
. Since there is no explicit j dependence inside the summation, this inner sum is simply and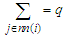 | (10) |
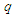 is equal to the number of neighbors of any given site, Eq.(10) into Eq.(9) give:
is equal to the number of neighbors of any given site, Eq.(10) into Eq.(9) give: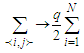 | (11) |
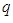 depends to the dimension of the system, for example, for a 1D lattice,
depends to the dimension of the system, for example, for a 1D lattice, 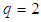 ; for a 2D triangular lattice,
; for a 2D triangular lattice, 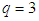 ; for a 3D square lattice,
; for a 3D square lattice, 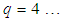
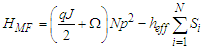 | (12) |
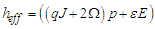 | (13) |
3. The Thermodynamics Parameters of the System
3.1. The Partition Function
- The partition function is one of the best tools which can allow us to derive the properties of a given system. Starting by definition, the partition function can be expressed as:
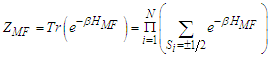 | (14) |
 and
and  by their values, the partition function becomes:
by their values, the partition function becomes: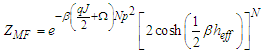 | (15) |
3.2. Total Polarization of System
- According to Eq.(6), the total polarization of MT’s system can be expressed as:
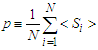 | (16) |
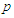 is the average polarization of the system.Knowing that the average value of the pseudo-spin is given by:
is the average polarization of the system.Knowing that the average value of the pseudo-spin is given by: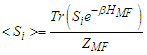 | (17) |
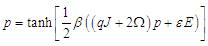 | (18) |
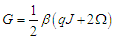 | (19) |
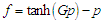 , In the absence of external field, the solutions are showed in Fig 1.
, In the absence of external field, the solutions are showed in Fig 1.3.3. Critical Temperature of the System and Phase Transition without the External Electric Field
- In this subsection, we going to use the non-zero and the zero polarization to characterize the state of the system as we previously mentioned in the introduction. We need to keep in mind that the non-zero polarization stands to the ferroelectric state; the zero-polarization stands to the paraelectric phase.In Fig.(1a),
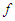 has three solutions:
has three solutions: 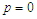 ;
; 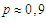 and
and 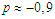 and
and 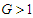 meaning that
meaning that 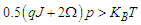 . As the system has a non-zero polarization, we conclude that the system is in the ferroelectric phase where
. As the system has a non-zero polarization, we conclude that the system is in the ferroelectric phase where 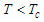 . This result suggests that the tubulin dimers are aligned in the best configuration which promotes the polymerization and organelle’s transport along with the network of the microtubule. In Fig.(1b),
. This result suggests that the tubulin dimers are aligned in the best configuration which promotes the polymerization and organelle’s transport along with the network of the microtubule. In Fig.(1b), 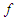 has one solution:
has one solution: 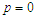 and
and 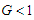 meaning that
meaning that 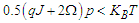 . As the system has a zero polarization, we conclude that the system is in the paraelectric phase where
. As the system has a zero polarization, we conclude that the system is in the paraelectric phase where 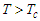 . Here the tubulin dimers are disordered, state that promotes depolymerization and deregulates the intracellular traffic.In Fig.(1c), we observed an ensemble of value range and
. Here the tubulin dimers are disordered, state that promotes depolymerization and deregulates the intracellular traffic.In Fig.(1c), we observed an ensemble of value range and 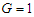 meaning
meaning 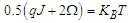 . We can be approved that, this phase corresponds to the transition from order to a disorder where
. We can be approved that, this phase corresponds to the transition from order to a disorder where 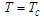 , and the critical temperature
, and the critical temperature 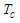 is derived by the following expression:
is derived by the following expression: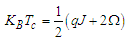 | (20) |
3.4. Polarization in Microtubules as a Function of Temperature
- In this subsection, the polarization behavior dependence on temperature will be studied in the absence and presence of the external electric field.• For
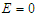 , and assuming that
, and assuming that 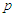 is very small near the critical temperature, let expand Eq.(18) as shown in Eq.(21).
is very small near the critical temperature, let expand Eq.(18) as shown in Eq.(21). 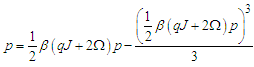 | (21) |
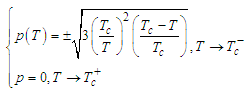 | (23) |
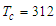 the system is in the ferroelectric phase and above
the system is in the ferroelectric phase and above 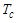 the system is in the paraelectric phase where the polarization vanishes after the critical temperature
the system is in the paraelectric phase where the polarization vanishes after the critical temperature 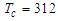 . The result confirms that the MT has a spontaneous polarization in absence of electric field and collapses after the physiological temperature of the human body [39].
. The result confirms that the MT has a spontaneous polarization in absence of electric field and collapses after the physiological temperature of the human body [39].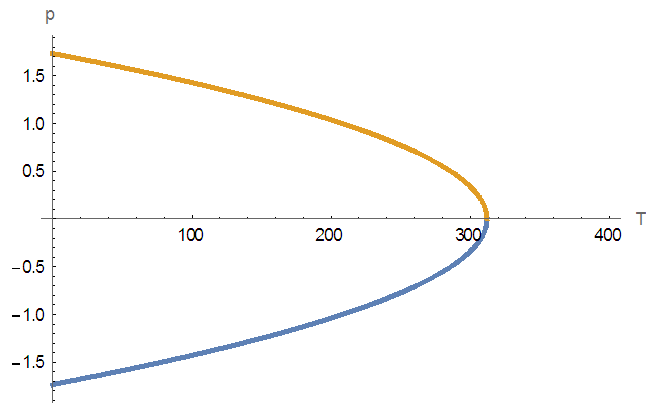 | Figure 2. Behavior of the polarization 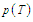 as a function of temperature as a function of temperature |
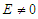 and assuming the same assumption previously used, we computed the polarization as:
and assuming the same assumption previously used, we computed the polarization as: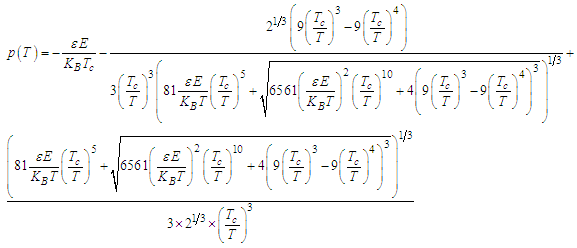 | (24) |
 | Figure 3. Polarization versus temperature, with  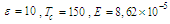 |
3.5. Free Energy
- We can also gain some useful insight into the physics of this system by looking at its (Helmholtz) free energy. Free energy is a mathematical function quantifying the work provided by a closed thermodynamic system during a reversible transformation at a constant temperature. The free energy of a system is minimal in the state of thermodynamic equilibrium. In microtubules, the energy given by the system comes from the hydrolysis process and thermal fluctuations at a high temperature which is an energy that promotes the depolymerization of microtubules. The microtubule is more stable if free energy is minimal. This energy is defined by:
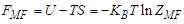 | (25) |
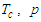 is small. We can so do a limited develop on
is small. We can so do a limited develop on 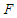 like and replace equation (15) in (25) we get:
like and replace equation (15) in (25) we get: 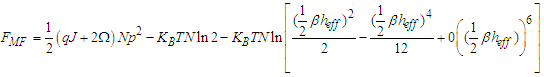 | (26) |
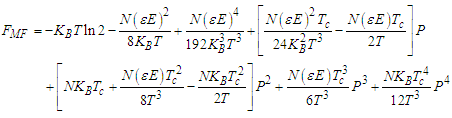 | (27) |
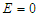 and
and 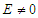 • For
• For 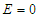 the free energy of this system is:
the free energy of this system is: 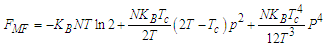 | (28) |
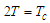 . The system control parameter is
. The system control parameter is 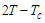 . If the latter is negative
. If the latter is negative 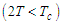 the system is in ferroelectric phase, positive,
the system is in ferroelectric phase, positive, 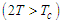 paraelectric phase. The 2 on the command, parameter comes from the anisotropy interaction considered in the system. For the Ising model without anisotropy interaction the control parameter is
paraelectric phase. The 2 on the command, parameter comes from the anisotropy interaction considered in the system. For the Ising model without anisotropy interaction the control parameter is 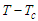 . From these results, we can conclude that anisotropy plays an important role in phase transitions. We plot
. From these results, we can conclude that anisotropy plays an important role in phase transitions. We plot 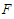 for
for 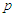 in Fig.4 for
in Fig.4 for 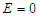 , we observe that: In the disordered phase
, we observe that: In the disordered phase 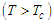 of the system, we have a single minimum p = 0. But in the ordered phase
of the system, we have a single minimum p = 0. But in the ordered phase 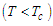 , energy becomes negative and we observe the appearance of two minima at values
, energy becomes negative and we observe the appearance of two minima at values 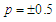 that they represent the points of stability of the system and a maximum
that they represent the points of stability of the system and a maximum 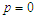 which is an instability point. Free energy in the ordered phase is smaller than in the disordered phase. From these results, we can conclude that: at low temperature
which is an instability point. Free energy in the ordered phase is smaller than in the disordered phase. From these results, we can conclude that: at low temperature 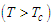 , the microtubules pass between the points of stability and dynamic instability. At high
, the microtubules pass between the points of stability and dynamic instability. At high 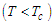 temperature the microtubules are unstable.
temperature the microtubules are unstable. 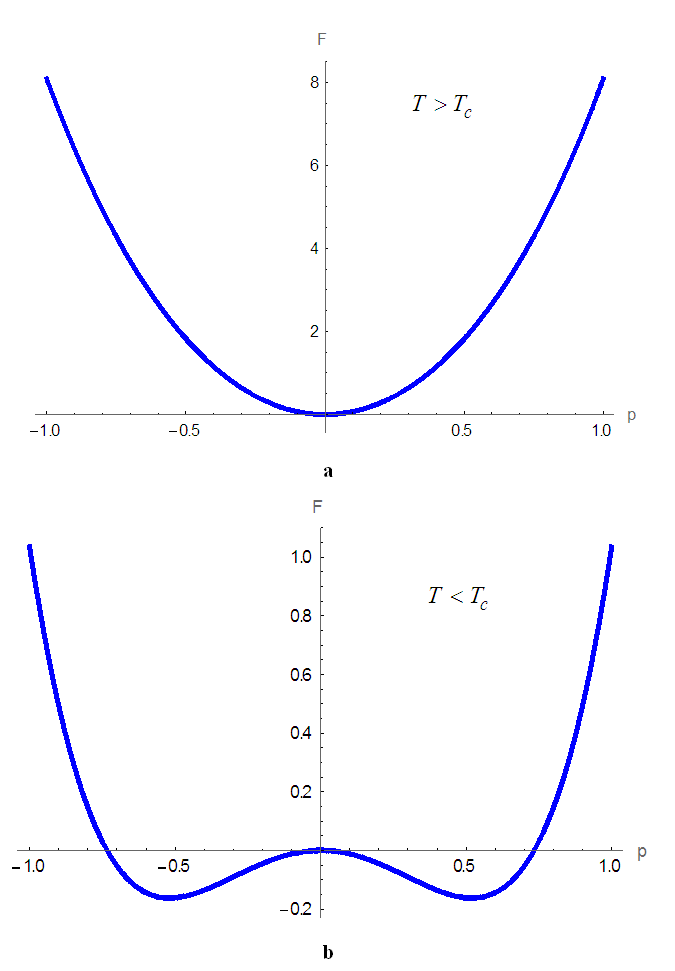 | Figure 4. Free energy a as function of mean polarization for    |
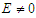 , the free energy of this system is:In Fig.5, we Plot free energy
, the free energy of this system is:In Fig.5, we Plot free energy 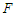 as a function of polarization
as a function of polarization 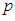 , In the presence of the electric field, we find that the free energy decreases when
, In the presence of the electric field, we find that the free energy decreases when 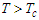 and
and 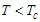 . In fig a, when
. In fig a, when 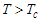 , the unstable solution
, the unstable solution 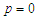 becomes a metastable solution. In Fig b, the increase in the electric field forces the metastable solution to orient in the direction of the field. We can conclude that: at high temperatures, the external electric field can stabilize the microtubules and orient them in the direction of the field. In figure c, for higher
becomes a metastable solution. In Fig b, the increase in the electric field forces the metastable solution to orient in the direction of the field. We can conclude that: at high temperatures, the external electric field can stabilize the microtubules and orient them in the direction of the field. In figure c, for higher 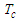 the electric field breaks symmetry with the disappearance of the point of instability
the electric field breaks symmetry with the disappearance of the point of instability 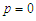 and directs the system towards single minimum energy. Thus, by applying an external electric field, we forced the system to choose one of the two solutions.
and directs the system towards single minimum energy. Thus, by applying an external electric field, we forced the system to choose one of the two solutions. 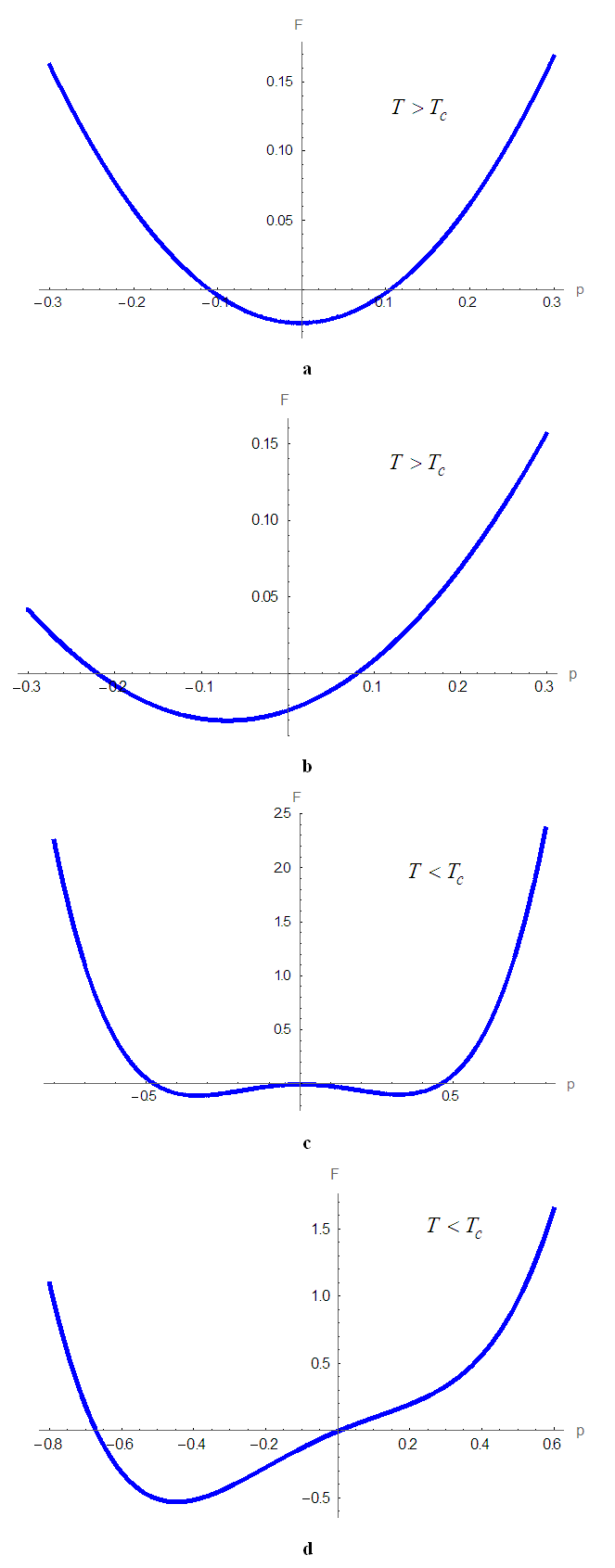 | Figure 5. Free energy a as function of mean polarization for 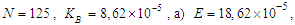 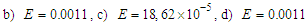 |
4. Conclusions
- In this work, we have studied the thermodynamic properties of microtubule that is developing in the absence and presence of an external electric field using the mean-field theory (MFT). We found the same parameters without the electric field and with the electric field in order to prove the effect of the external electric field on the microtubule dynamics. Numerical results obtain put forward the dynamic instability phenomenon which occurs in microtubule by the self-organization process. It is clearly shown that the breaking symmetry of the system strongly depends on the magnitude of the external electric field and the value of temperature. So the study of MT in the presence of external field exhibits phase transitions from the ferroelectric phase to paraelectric one and sometimes the metastable phase where both coexist in solution. We have just shown that: at low temperatures, the electric field increases the stability of microtubules; at high temperatures, this field increases the critical temperature which allows the transition from the ordered state of the dipoles to the disordered state of the electric dipoles. We also show that the increase in the field makes it possible to direct the electric dipoles in the direction of the field. Then this electric field can also be used to control the direction of the microtubule which will be very important in the transport of information in the cells.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML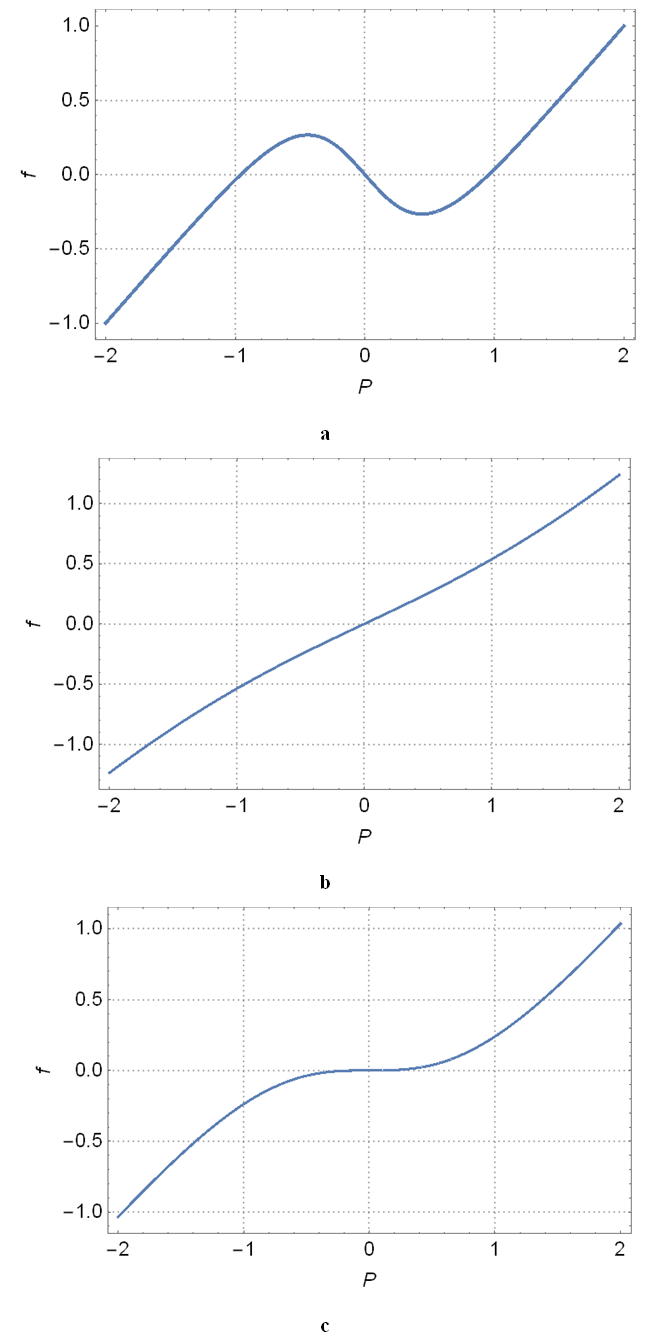
 . For a):
. For a):  ; For b):
; For b):  ; For c):
; For c):