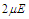-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Biophysics
p-ISSN: 2168-4979 e-ISSN: 2168-4987
2020; 10(1): 9-16
doi:10.5923/j.biophysics.20201001.02
Received: July 1, 2020; Accepted: August 6, 2020; Published: August 29, 2020

Dynamics of Microtubule Pseudo-Spin under the Influence of External Electric Field
C. Kenfack-Sadem, W. A. Nganfo, M. C. Ekosso, S. N. Wopunghwo, M. F. C. Fobasso, A. J. Fotué, L. C. Fai
Condensed Matter and Nanomaterials, Faculty of Science, Department of Physics, University of Dschang, Cameroon
Correspondence to: C. Kenfack-Sadem, Condensed Matter and Nanomaterials, Faculty of Science, Department of Physics, University of Dschang, Cameroon.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, the longitudinal polarization (order parameter) and electric susceptibility in the microtubule system have been investigated in the absence and presence of an external electric field using the mean-field approximation (MFA). We analyzed the behavior of the pseudo-spins inside the tubulin dimers by the transverse Ising approximation. We found out that in the absence of the electric field, the coupling constant of spin-spin interaction and anisotropic interaction bring the system in a ferroelectric (FE) phase while high temperatures and transverse fields bring the transition to paraelectric (PE) phase. Moreover, the presence of an external electric field increases the critical temperatures and brings the hysteresis phenomenon in the microtubule system.
Keywords: Microtubule, Polarization, Transverse field, Ferroelectric phase, External electric field, Temperature
Cite this paper: C. Kenfack-Sadem, W. A. Nganfo, M. C. Ekosso, S. N. Wopunghwo, M. F. C. Fobasso, A. J. Fotué, L. C. Fai, Dynamics of Microtubule Pseudo-Spin under the Influence of External Electric Field, International Journal of Biophysics , Vol. 10 No. 1, 2020, pp. 9-16. doi: 10.5923/j.biophysics.20201001.02.
1. Introduction
- The cytoskeleton is an assembly of multiple proteins connect together in order to give and maintain cell and membrane shape. In the cytoskeleton, there are three types of filament namely: actin filaments, intermediate filaments, and microtubules (MTs) [1,2]. MTs, major elements of the cytoskeleton are supposed to be the center of cellular organization and information processing. They play an important role in intracellular transport where they serve as road-rail for motors proteins, essential during cell division and cell motility [3,4]. For example, the coronavirus, hepatitis C virus, and many other viruses interact with microtubules directly or indirectly by associating with motor proteins [5] to move through the multiplication areas of the cell and facilitate replication of the virus. The perturbation of the displacement of microtubules associated with the coronavirus slows the replication of the virus [6-8].It had been shown that MT is a long cylindrical tube about 25nm in outer diameter and 14nm in inner diameter. The interior of the cylinder is likely to be filled with ordered water, which implies the existence of electric dipoles and electric fields [9,10]. Forms by 13 protofilaments, MTs are extremely dynamic and unstable because of the dynamic behavior of its basic units call tubulin dimers that attach end to end to form a protofilament [11,12]. Each tubulin dimer consists of two elements, α tubulin negatively charged and β tubulin positively charged. This polarity difference implies that MTs are polarized structures where tubulin dimers are seen as electric dipoles [13,14]. There is an unbound mobile electron on each dimer, which can be localized to either α tubulin or β tubulin. Thus, depending on the location of the mobile electron, the tubulin dimer has two basic states as shown in Fig.1. These states are pseudo-spins where one can be spin up and another spin down depending on the mobility of electrons in the tubulin dimer [15,16]. In agreement with the behavior of ferroelectric (FE) materials to have a spontaneous electric polarization whose direction of polarization can be reversed under the action of an electric field [17-20], it has been hypothesized that MTs are oriented assemblies of electrical dipoles and can be assimilated to ferroelectric systems [21]. In ferroelectric systems, polarization is considered as the order parameter to describe the entire system. In classical electrodynamics, it is a macroscopic quantity defined as the average of the local contribution of elementary dipole moments and quantifies the transition from ferroelectric to paraelectric (PE-PE) phase [22,23]. In general, the system is usually considered in the ordered state or ferroelectric state when spins align in the same direction for increasing the polarization. In this case, it is possible to orientate the information in a precise direction. When the polarization gets to zero the system goes from ferroelectric to disorderly or paraelectric (PE) state because the spins are oriented in several directions where the information has not easily controlled.
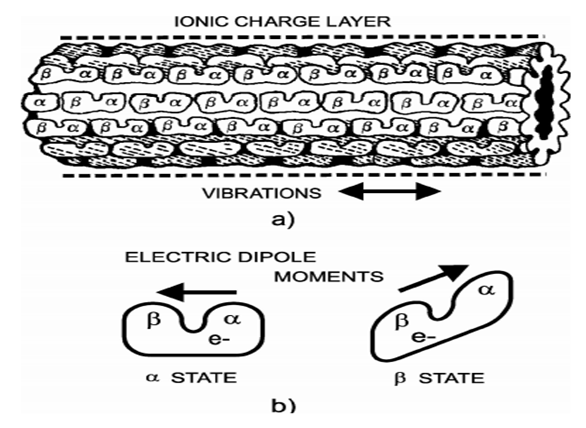 | Figure 1. (a) Microtubule formed by protofilaments composed of tubulin heterodimers. (b) Heterodimer in α and β conformation state; the arrows denote the vectors of the electrical dipoles [14] |
2. Model and Calculations
- According with the work proposed by Chen Ying et al. [15] and that of Cifra et al. [28], we consider MT as a nonlinear ferroelectric chain made up of N pseudo-spin sites where anisotropic interaction [29,30] is taking into account. And then, we define the system using the Hamiltonian of the ferroelectric chain as:
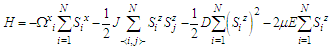 | (1) |
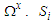 And
And 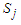 represent the pseudo-spin respectively in site i and site j with
represent the pseudo-spin respectively in site i and site j with 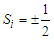 . The second term characterizes the nearest -neighbor exchange interaction energy between the spin of the site i and the spin of the site j, with an interaction coupling
. The second term characterizes the nearest -neighbor exchange interaction energy between the spin of the site i and the spin of the site j, with an interaction coupling 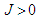 . The notation
. The notation 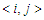 meaning that the sum is restricted to the nearest-neighbor pair of pseudo-spin, each pair being counted only once [31]. The third term represents anisotropic interaction, where
meaning that the sum is restricted to the nearest-neighbor pair of pseudo-spin, each pair being counted only once [31]. The third term represents anisotropic interaction, where 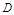 is the anisotropic coefficient along the z-axis [32,33]. The last term represents the longitudinal external electric field and
is the anisotropic coefficient along the z-axis [32,33]. The last term represents the longitudinal external electric field and 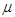 denotes the electric dipole moment. Using the mean-field approximation (MFA) [15,34,35] we compute the effective Hamiltonian of the system using
denotes the electric dipole moment. Using the mean-field approximation (MFA) [15,34,35] we compute the effective Hamiltonian of the system using 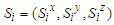 as a vector, its components are three Pauli matrices of the pseudo spin. Assuming that the density matrix
as a vector, its components are three Pauli matrices of the pseudo spin. Assuming that the density matrix 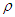 of the many-body system equal to the product of the single-particle density matrices
of the many-body system equal to the product of the single-particle density matrices 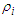 expressed as:
expressed as: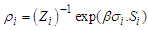 | (2) |
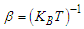 with
with 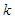 the Boltzmann constant,
the Boltzmann constant, 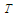 the temperature and
the temperature and 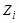 the partition function of a single-particle express as [15]:
the partition function of a single-particle express as [15]: 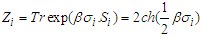 | (3) |
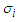 denotes the effective field exerting on
denotes the effective field exerting on 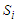 defines as:
defines as: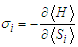 | (4) |
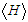 the thermodynamic expectation value of the Hamiltonian
the thermodynamic expectation value of the Hamiltonian 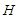 .By using the sum over nearest-neighbors defined as
.By using the sum over nearest-neighbors defined as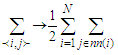 , where the factor of
, where the factor of 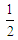 is to avoid double counting pairs of sites and
is to avoid double counting pairs of sites and 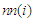 denotes nearest-neighbors of
denotes nearest-neighbors of 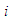 . Since there is no explicit j dependence inside the summation, this inner sum is simply and
. Since there is no explicit j dependence inside the summation, this inner sum is simply and 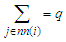 where the coordination number
where the coordination number 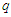 is equal to the number of neighbors of any given site.The value of
is equal to the number of neighbors of any given site.The value of 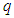 depends on the dimension of the system, for example, for a
depends on the dimension of the system, for example, for a 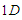 lattice,
lattice, 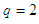 ; for a
; for a 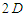 triangular lattice,
triangular lattice, 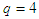 ; for a
; for a 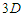 square lattice,
square lattice, 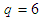 . Assuming all these assumptions and consider
. Assuming all these assumptions and consider 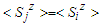 , the final expression of the effective field is given by:
, the final expression of the effective field is given by: 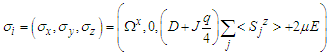 | (5) |
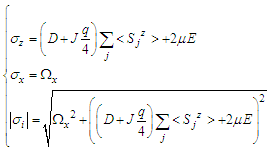 | (6) |
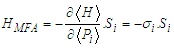 | (7) |
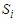 is expressed as:
is expressed as: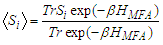 | (8) |
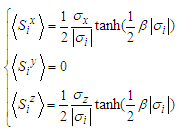 | (9) |
 of the system is proportional to the thermal mean of the pseudo spin which is well defined in Ref. [33] by:
of the system is proportional to the thermal mean of the pseudo spin which is well defined in Ref. [33] by: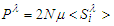 | (10) |
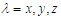 and
and 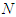 represents the number of dimers in the microtubule and
represents the number of dimers in the microtubule and 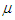 designates the single electric dipole.Using Eq (10), the expressions of longitudinal polarization and susceptibility for the system are respectively giving by:
designates the single electric dipole.Using Eq (10), the expressions of longitudinal polarization and susceptibility for the system are respectively giving by: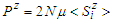 | (11) |
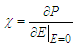 | (12) |
3. Results and Discussions
- In this section, we will compute numerically the longitudinal polarization and the electric susceptibility under the influence of various parameters such as spin-spin interaction, anisotropic interaction, and external field. Temperature greatly influences the dynamics of MTs and its variations show complex phenomena in living systems [36]. So, we will plot the polarization and the susceptibility as a function of temperature. Our main goal is to study the influence of these parameters on the transition of the ferroelectric phase to the paraelectric phase in the MT system. In Fig.2, we have plotted the temperature dependence of the longitudinal polarization (Fig.2a) and the susceptibility (Fig.2b) in the absence of the external electric field at different values of the coupling constants of the tubulin dimers considering a specific value of the transverse field
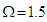 .It is shown that the polarization is a decreasing function of environmental temperature (Fig.2a), meaning that spins that form MT have the tendency to depolarize when the temperature of the system increases. High temperatures bring the system in PE state and mess up the orientation of the information in a specific direction. By considering the variations of coupling constantly related to spin-spin interaction and the anisotropic interaction, it is shown that the increase of coupling constant in the tubulin dimers leads to an increase in longitudinal polarization. Meaning that the increase of coupling constant tends to bring the system in a ferroelectric phase. The transition of the system from FE to PE will be delayed when the chemical displacement and the anisotropic interaction between the spins increase, the same results were obtained in [33].In Fig.2b, the susceptibility dependence on temperature shows two behaviors, an increase behavior at low temperatures and a decrease behavior at high temperatures supposing that the MT system has a strong capacity to polarize at low temperatures; this result is in agreement with the result previously obtained in Fig.2a. For each value of the coupling constant, one can observe the critical point of susceptibility corresponding to the point where the polarization decreases to bring the system toward PE state. Moreover, these critical points correspond to critical temperatures that increase with increase the coupling constant. At high temperatures, the susceptibility is identical for the different values of the coupling constant, meaning that the coupling constant does not affect the polarization state of the system.
.It is shown that the polarization is a decreasing function of environmental temperature (Fig.2a), meaning that spins that form MT have the tendency to depolarize when the temperature of the system increases. High temperatures bring the system in PE state and mess up the orientation of the information in a specific direction. By considering the variations of coupling constantly related to spin-spin interaction and the anisotropic interaction, it is shown that the increase of coupling constant in the tubulin dimers leads to an increase in longitudinal polarization. Meaning that the increase of coupling constant tends to bring the system in a ferroelectric phase. The transition of the system from FE to PE will be delayed when the chemical displacement and the anisotropic interaction between the spins increase, the same results were obtained in [33].In Fig.2b, the susceptibility dependence on temperature shows two behaviors, an increase behavior at low temperatures and a decrease behavior at high temperatures supposing that the MT system has a strong capacity to polarize at low temperatures; this result is in agreement with the result previously obtained in Fig.2a. For each value of the coupling constant, one can observe the critical point of susceptibility corresponding to the point where the polarization decreases to bring the system toward PE state. Moreover, these critical points correspond to critical temperatures that increase with increase the coupling constant. At high temperatures, the susceptibility is identical for the different values of the coupling constant, meaning that the coupling constant does not affect the polarization state of the system. 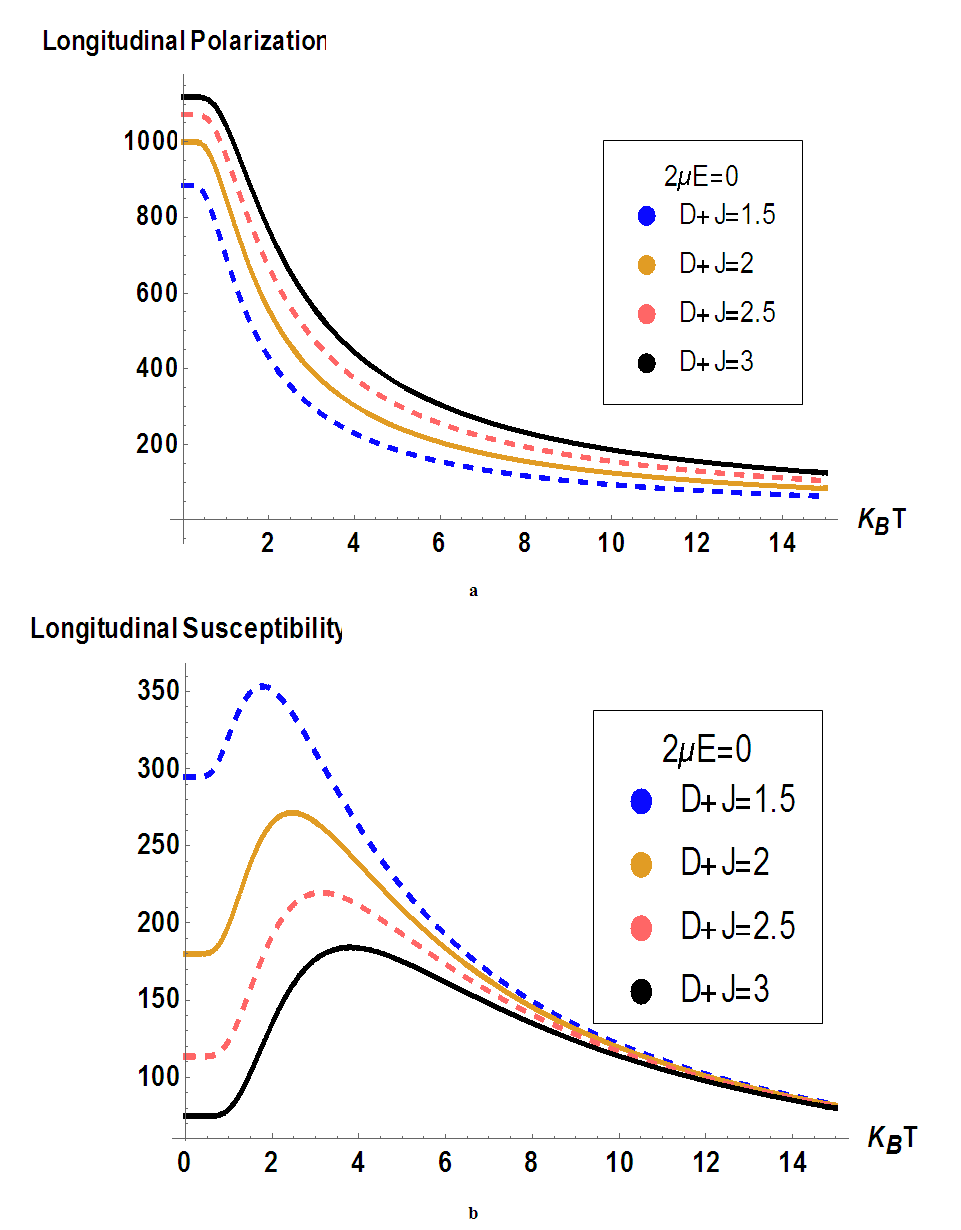 | Figure 2. a) Longitudinal polarization as a function of temperature for different values of the coupling constants; b) Susceptibility versus temperature for different values of the coupling constants |
 by considering different values of the transverse field
by considering different values of the transverse field  . In Fig.3a, it is shown that by increasing the transverse field, the polarization decreases. So, the stronger is a transverse field and the weaker is the polarization of the MTs system. At high temperatures, the polarization is identical for the different values of the transverse field. Fig.3b shows the susceptibility as a function of temperature. It is observed that critical points disappear by increasing the transverse field. These results suggest that the presence of the transverse field in the system disturbs the orientation of the pseudo spins in the tubulin dimers and brings the system into PE state.
. In Fig.3a, it is shown that by increasing the transverse field, the polarization decreases. So, the stronger is a transverse field and the weaker is the polarization of the MTs system. At high temperatures, the polarization is identical for the different values of the transverse field. Fig.3b shows the susceptibility as a function of temperature. It is observed that critical points disappear by increasing the transverse field. These results suggest that the presence of the transverse field in the system disturbs the orientation of the pseudo spins in the tubulin dimers and brings the system into PE state. for a transverse field
for a transverse field 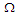 and the coupling constant
and the coupling constant 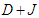 . The presence of a strong external electric field increases the polarization (see Fig.4a). This figure exhibits the same behavior that Fig.2a but, it is clearly shown that the range of polarization in this case, is higher than in Fig.2a. The behavior of the susceptibility is the same as that de Fig.2b. But in the presence of an external electric field, the critical temperatures are higher than those in Fig.2b. Meaning that the external electric field keeps the system in FE state [37]. In this case, the transition from FE to PE occurs later than in the absence of an external electric field.
. The presence of a strong external electric field increases the polarization (see Fig.4a). This figure exhibits the same behavior that Fig.2a but, it is clearly shown that the range of polarization in this case, is higher than in Fig.2a. The behavior of the susceptibility is the same as that de Fig.2b. But in the presence of an external electric field, the critical temperatures are higher than those in Fig.2b. Meaning that the external electric field keeps the system in FE state [37]. In this case, the transition from FE to PE occurs later than in the absence of an external electric field. 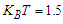 and a given transverse field
and a given transverse field 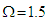 . It is shown that the polarization increases by increasing the coupling constant. If the interaction between pseudo spins that form the MT changes when the external electric field varies, the system exhibits the hysteresis phenomenon. This result confirms the ferroelectric and nonlinear character of the MT system.
. It is shown that the polarization increases by increasing the coupling constant. If the interaction between pseudo spins that form the MT changes when the external electric field varies, the system exhibits the hysteresis phenomenon. This result confirms the ferroelectric and nonlinear character of the MT system.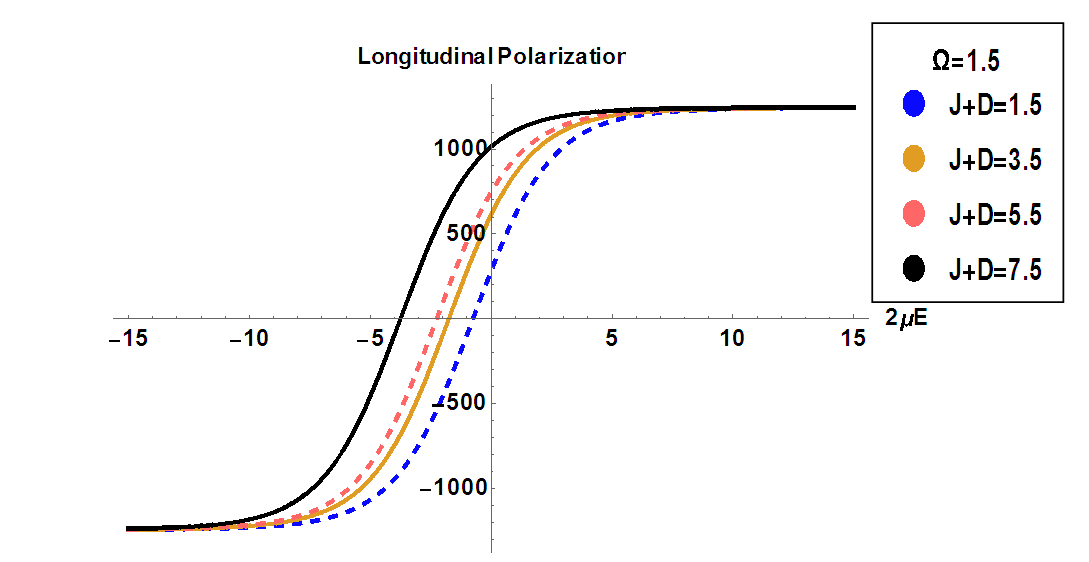 | Figure 5. Longitudinal polarization as a function of the electric field  at different values of coupling constant at different values of coupling constant |
 , at constant temperature
, at constant temperature  by varying the transverse field
by varying the transverse field 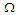 . It is observed that the increase of the transverse field decreases the longitudinal polarization. So, increasing the transverse field destroys the hysteresis of the system.
. It is observed that the increase of the transverse field decreases the longitudinal polarization. So, increasing the transverse field destroys the hysteresis of the system. 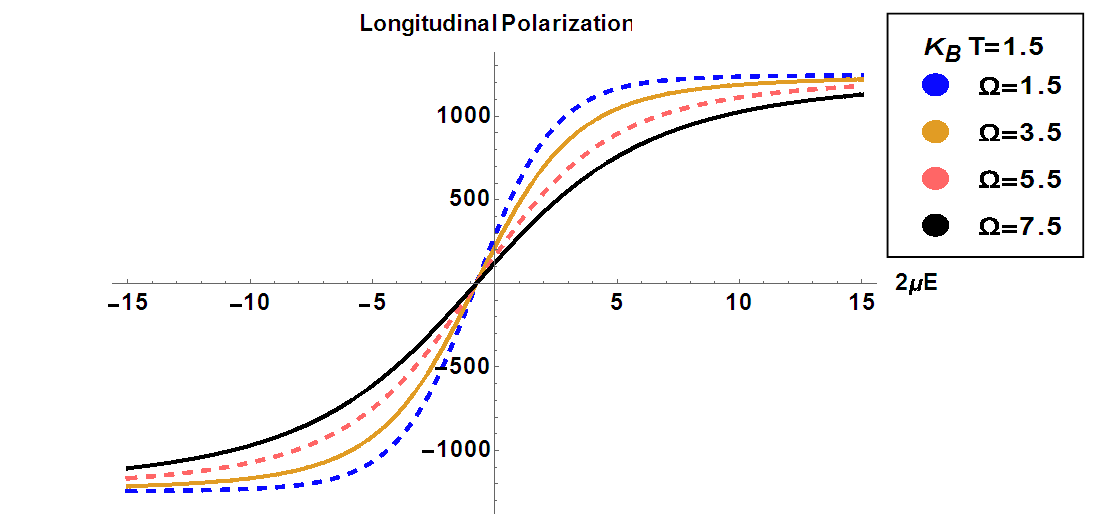 | Figure 6. Longitudinal polarization as a function of the electric field  at different values of the transverse field at different values of the transverse field |
4. Conclusions
- In this work, by assuming microtubule system as an ensemble of N pseudo spins, we computed the longitudinal polarization and susceptibility using the mean-field approximation (MFA) in the absence and presence of the external electric field. In order to control the orientation of information in a specific direction, we studied the system in the absence of an external electric field by considering the influence of spin-spin interaction, anisotropic interaction and constant transverse field. The results obtained show that the increase of coupling constant brings the system in a ferroelectric phase while high temperatures bring the transition to the paraelectric phase. This last result was also obtained by studying the influence of the transverse field at a constant interaction coupling. In the presence of an external electric field, the critical temperature increase more than in the absence of an external electric field. In this case, the system is maintained in the ferroelectric configuration and exhibited the hysteresis phenomenon that is destroyed by increasing the transverse field in the system. The external electric field can be used to control the direction of information in the microtubules. Thus, the transverse field and temperature promote the paraelectric phase while spin-spin interaction, anisotropic interaction and external electric field maintain the MT system in the ferroelectric phase.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
 . b) Susceptibility as a function of temperature for different values of the transverse field
. b) Susceptibility as a function of temperature for different values of the transverse field 
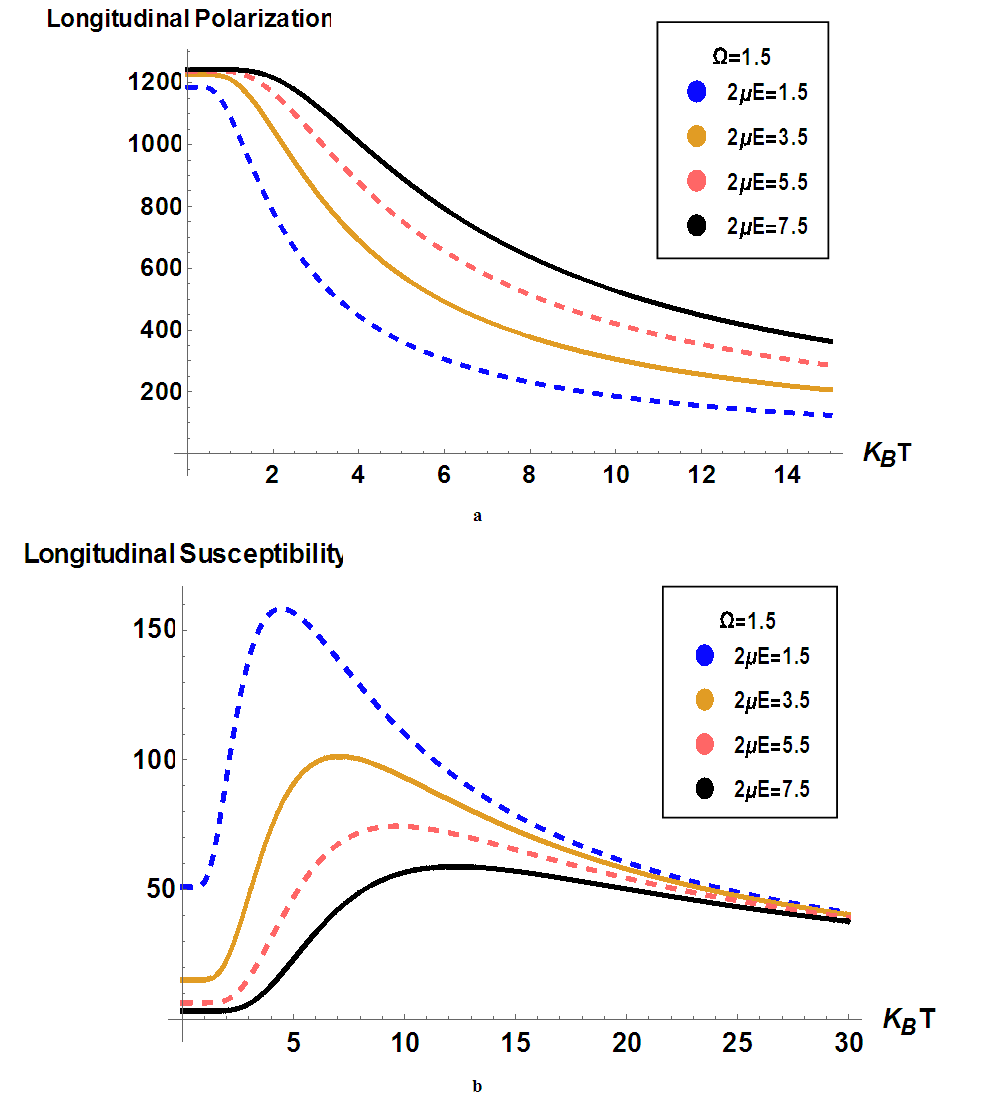
 . b) Longitudinal susceptibility as a function of temperature for different values of the electric field
. b) Longitudinal susceptibility as a function of temperature for different values of the electric field