-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Biophysics
p-ISSN: 2168-4979 e-ISSN: 2168-4987
2019; 9(1): 1-11
doi:10.5923/j.biophysics.20190901.01

Thermodynamic Evaluation of Electrical Responses to Odorant in Olfactory Sensory Neurons
Samantha Hagerty, Melissa Singletary, Oleg Pustovyy, Ludmila Globa, Edward E. Morrison, Iryna Sorokulova, Vitaly Vodyanoy
Department of Anatomy, Physiology and Pharmacology, Auburn University College of Veterinary Medicine, Auburn, Alabama, USA
Correspondence to: Iryna Sorokulova, Vitaly Vodyanoy, Department of Anatomy, Physiology and Pharmacology, Auburn University College of Veterinary Medicine, Auburn, Alabama, USA.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The thermodynamic properties of olfactory sensory receptors were characterized by the measurement of electrical responses to odorants in isolated olfactory epithelia. Using the electroolfactogram (EOG), electrical activity was recorded within a temperature range of 16°C–35°C with epithelia obtained from animals being kept at ambient environmental conditions. The amplitude, the area under the curve, and the voltage kinetics of the electroolfactogram recordings were measured at different temperatures. The apparent values of the activation energy and the change of enthalpy (ΔH), entropy (ΔS), and Gibbs free energy (ΔG) of the odorant-receptor interaction were estimated using both Arrhenius and Eyring equations. The results reveal a broad variation of enthalpy (ΔH) and entropy contribution (TΔS) for odorant interaction with different sets of olfactory receptors. The observed enthalpy change was always followed by a corresponding change in the entropy contribution (TΔS), maintaining constant free energy (ΔG): ΔG=ΔH-TΔS and obeying the enthalpy-entropy compensation. Notably, in all experiments, the changes in enthalpy or entropy do not correlate with the change of free energy. Due to the fact that the values of ΔH and TΔS represent a summation of all chemical interactions between odorant and olfactory sensory neuron, it is difficult to expect the binding properties of odorants to serve as a foundation of molecular recognition by olfactory receptors. For this reason, our thermodynamic results do not support the shape mechanism of olfaction.
Keywords: Electroolfactogram, Shape model, Vibrational model
Cite this paper: Samantha Hagerty, Melissa Singletary, Oleg Pustovyy, Ludmila Globa, Edward E. Morrison, Iryna Sorokulova, Vitaly Vodyanoy, Thermodynamic Evaluation of Electrical Responses to Odorant in Olfactory Sensory Neurons, International Journal of Biophysics , Vol. 9 No. 1, 2019, pp. 1-11. doi: 10.5923/j.biophysics.20190901.01.
Article Outline
1. Introduction
- The sense of smell is not just crucial for animal survival [1]; it also assumes importance for human health, emotional connections, and social interactions [2-4]. The initial events of olfaction take place within the olfactory neuroepithelium situated in the posterior nasal cavity. Olfactory sensory neurons (OSNs) are bipolar neurons with a single axonal end extending basally and a dendritic end that extends apically towards the nasal cavity airway. OSNs direct their unbranched axons to the olfactory bulb (OB), passing through the cribriform plate. Within the OB, the OSNs axons form contact with secondary neurons (mitral and other cells) in spherical neuropils, called glomeruli. OSNs have a few dozen hair-like cellular structures, referred to as olfactory cilia. Cilia harbor the sensory apparatus (olfactory receptor (OR) proteins and other components) that converts and amplifies the physical-chemical signal of the odorant molecule into electric current [5]. The processes of signal transduction have been studied and described extensively [6], and is thought to be well characterized. However, the primary molecular mechanism of odorant recognition in olfaction remains contentious. The vibrational mechanism of olfaction was suggested in 1937 by Dyson [7, 8] being exposed to contemporary Raman Spectroscopy. Dyson opined that the molecular vibrations correlate with the properties of odorant in a range of 1,400-3500 cm-1. Later, Wright modified Dyson’s model by considering vibrations below 700 cm-1 that he deemed more suitable for the whole odorant molecule as opposed to for specific functional groups [9, 10]. The vibrational mechanism of olfaction was not actively researched and remained dormant for many years until Luca Turin reincarnated it in 1996 [11]. Turin proposed an inelastic electron tunneling spectroscopy (IETS) mechanism to discriminate odors. Under the IETS model, the odorant mediates inelastic tunneling of an electron between donor and acceptor inside the receptor. The donor and acceptor differ in energy by ћωo (phonon energy), so that tunneling of an electron occurs only when the energy is adsorbed by an odorant’s phonon. Turin posited that the electron tunneling leads to the release of the G-protein, which in turn initiates the olfactory signal cascade. The vibrational mechanism has been developed further theoretically and examined experimentally by Turin along with many other scientists. For recent review, refer to [12]. The alternative mechanism of olfaction is based on the lock-and-key model originally offered for the ligand-protein interaction [13]; later, the general concept was used in the Moncrieff and Amoore shape-stereochemical-steric mechanism controlling olfaction [14-17]. This model in the present interpretation suggests that shape, size, and functional groups of odorant determine the activation of olfactory receptors. A variety of physical forces and interactions are suggested to interplay in order to support this model of olfaction. The list contains electrostatic ion-ion and proton acid-base interactions, hydrogen-bonding, halogen bonding, charge-transfer and π–π molecular complexation, dipolar and multipolar interactions, and van der Waals interactions [18]. These forces were somewhat narrowed in consideration of binding of the odorant and the odorant binding pocket via hydrophobic and van der Waals interactions [19]. In order to satisfy the fact that each odorant is recognized by multiple olfactory receptors, and that each receptor can bind multiple odorants [20], the simple “lock-and-key” model was replaced by the “induction fit” and “conformational selection” models, where shape of the odorant does not exactly fit to the shape of the receptor; instead, both odorant and receptors may experience conformational transformations [21]. The efficacy of odorants in activating receptors was attributed to a gamut of factors including “tight interaction with the floor of the binding pocket” [22], odorant functional groups specific hydration [23], odorant molecular shape [24], odorant size and hydrophobicity [25], volume and structural flexibility [26], odorant-receptor binding kinetics [27] and binding affinity of odorant to receptor [28]. Without according preference to the “shape” or “vibrational model”, it would be fair to surmise that the present “shape” model of olfaction goes over and above the original straightforward, elegant, and clear concept of Moncrieff and Amoore model, involving numerous interactions and factors that are suggested to be vital for olfactory recognition. Notably, the binding chemistry and binding affinity of odorants to receptors are important requirements of the contemporary shape model. The shape and vibration models have been debated extensively [29, 30]. The proponents of the vibrational model primarily contend that animals and humans can discriminate isotopic odorants that have replaced hydrogen or carbon with heavier atoms. Although the molecules preserve their shape, they are known to change mass and consequently, the frequency of vibration [31-35]. Meanwhile the supporters of “shape” models of olfaction argue that the chemical properties of odorants with replaced atoms are different from the original unaltered molecules. Therefore, the interaction of the isotope odorant with mucus and binding inside the receptor may be responsible for the discrimination of odorant-isotopes [29]. We question the importance of the binding properties between odorants and olfactory receptors for the odorant recognition. In this work, we have analyzed the kinetic and thermodynamic properties of electroolfactogram (EOG) [36] which is the transient electrical response of OSNs to a short pulse of odorant stimulation. The objective of the study is to characterize the initial events in olfactory transduction thermodynamically when the complicated multistep biophysical process underpinning the EOG is depicted by the transition over a single potential barrier. This approach allows the quantification of activation energy, as well as the change of enthalpy, entropy, and Gibbs free energy of this transition. Furthermore, it enables us to look at the controversial “shape” and “vibrational” models from a different perspective.
2. Material and Methods
2.1. Animals
- The animal protocol was approved by the Auburn University Institutional Animal Care and Use Committee (AU IACUC). Adult male Sprague–Dawley rats (Envigo, Dublin, VA) weighing ~300 g were used.
2.2. Odorants
- Odorants were obtained from Sigma-Aldrich. An odorant mixture of 1.6 mmole/L each of ethyl butyrate, eugenol, and (+) and (–) carvone in water was prepared with a vortex mixer and stored in a dark glass container at 283K (5°C). This odorant mixture had been previously used in our research [37, 38] (Supplementary information).
2.3. Experimental Design
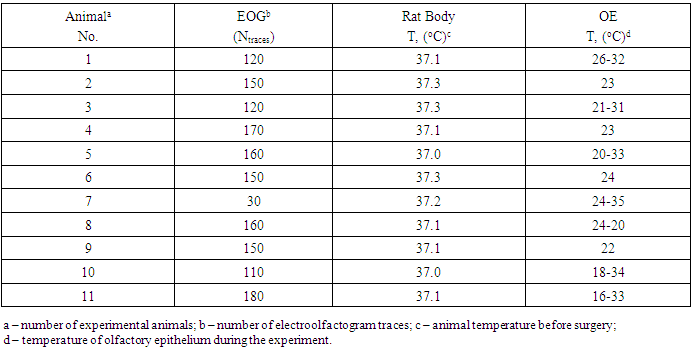
- The kinetics of olfactory sensory responses to odorants were measured by the electroolfactogram (EOG) of isolated rat olfactory epithelium at the temperature-controlled conditions. A total of 11 rats were divided into two groups. One group (negative control) comprising of four rats were tested and the EOG of extracted olfactory epithelia were measured at a constant temperature. The second group of seven animals was examined and the EOG of extracted olfactory epithelia were measured at various temperatures ranging between 16-35°C. The kinetics of olfactory responses to odorants were used to calculate the thermodynamic parameters of EOG at given conditions.
2.4. Electroolfactogram Recording
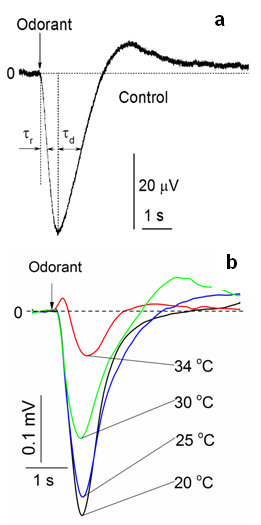
- Rat OE was dissected and positioned in a perfusion chamber such that the basal parts were immersed in buffer solution [37]. The EOG measuring electrode with the opening of ~24 μm in diameter could cover ~50 neurons. On average, 140 EOG traces were made at the single contact of the electrode with olfactory epithelium. A single contact recording took ~ 40 minutes, and one recording was undertaken per one olfactory epithelium. All olfactory experiments were performed ex vivo. Odor-activated current clamped voltage responses were recorded as EOG with an integrating patch clamp amplifier (MultiClamp 700A Amplifier, Molecular Devices). The analog signal was filtered at 0-5 kHz and digitized using a digital converter (DigiData 1322 A). Data acquisition, storage and subsequently, analysis was carried out using pCLAMP software (Axon Instruments) and exported in ASCII format for further analysis. The recording chamber was enclosed in a grounded Faraday box on a vibration isolation table (GS-34 Newport) (Supplementary information). EOG responses were analyzed to determine half-rise and half-decay times. The EOG signal typically rises to achieve a maximal level before decaying to the initial value. Notably, the half-decay time is defined as the time needed for the EOG signal to decay from the maximum level to half of maximal amplitude [39]. The representative EOG trace is illustrated in Figure 1 a.
2.5. Stability of Olfactory Responses to Odorant
- Due to significant variability of odorant responses by individual cells, it was important to ensure stability over an extended period and response reproducibility at a single contact. Olfactory epithelia were also evaluated for responsiveness to odorants and stability. Repeatable recordings of consecutive 0.25-s odorant pulses were produced at 200-s at steady-state conditions. The patch clamp amplifier stability was also examined.
2.6. Delivery of Odorants
- The odorant vapor was produced by homemade olfactometer [26] that was used for the precise computer-controlled delivery of pre-determined quantities of odorants over a programmed time interval (Supplementary information). For stimulation purposes, a 0.25 s pulse of the odorant mixture at 8 pounds per square inch was formed by the computer-controlled olfactometer and Pneumatic PicoPump PV800 (World Precision Instruments, Sarasota, FL, USA). A pulse of positive pressure drove the odorant into a glass nozzle directed at the OE. The residual odorant was cleared by air between each stimulus application. The odorant pulse patterns were initiated either manually at predetermined time intervals or automatically by computer. The automatic computer routine comprised of 0.25 s pulses at 20 s intervals. One series of 10 pulses at 20 s intervals constituted one ‘EOG recording.’ Thus, in the automatic regime, the duration of a single ‘EOG recording’ was 200 s and was able to correspond to 10 response traces. The water/air partition coefficient for all odorants used in our experiments is very low (~10-4), and the concentration of odorants delivered to olfactory epithelia is of ~ 100 nM range (Supplementary information).
2.7. Temperature-controlled EOG Perfusion Chamber
- The perfusion chamber was positioned into the aluminum plate with heating elements controlled by an Automatic Temperature Controller C TC 324 (Warner Instruments, Hamden, CT USA). Thereafter, the temperature was measured by a thermistor with an accuracy of 0.01 oC before being synchronized and recorded continually with the EOG signals. (Supplementary information, Figure S3). The temperature of the perfusion chamber with OE could be maintained within a range of 16-35°C. The steady state temperature was held at ±0.1°C, and transition between different temperatures was achieved at the rate of ~1.5 degrees/minute. The chamber with OE was perfused at 10 mL/h by a Peristaltic Pump P-1 (Pharmacia Fine Chemicals Inc, Piscataway, NJ, USA).
2.8. Thermodynamic Calculations of the EOG Measured at Different Temperatures
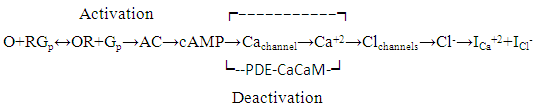
- The ion currents resulting from the interaction of odorants with olfactory sensory receptors cause the transmembrane potential difference in the cilia, known as a generator potential. The EOG represents the sum of generator potentials of olfactory receptor neurons. EOG can be recorded by an electrode placed on the surface of the olfactory mucosa as the mucosa is subjected to an odorous stimulus [36].The simplified diagram of signal transduction can be illustrated as follows:
 | (1) |
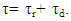 | (2) |
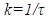 | (3) |
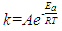 | (4) |
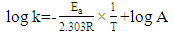 | (5) |
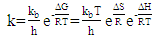 | (6) |
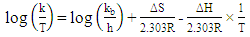 | (7) |
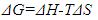 | (8) |
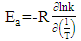 | (9) |
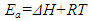 | (10) |
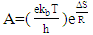 | (11) |
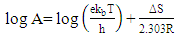 | (12) |
 | (13) |
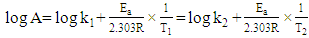 | (14) |
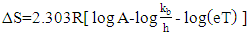 | (15) |
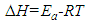 | (16) |
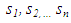 | (17) |
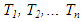 | (18) |
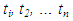 | (19) |
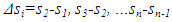 | (20) |
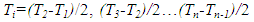 | (21) |
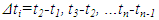 | (22) |
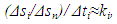 | (23) |
2.9. Statistical Analysis
- Data averaging, ANOVA, t-test, curve fitting, and graph plotting were conducted using Origin 2015 (Northampton, MA, USA) and 2010 Microsoft Excel.
3. Results
3.1. Stability and Repeatability of Olfactory Responses to Odorant
- Response amplitude was found to be fairly stable during repetitive odorant application. Notably, the mean values of the relative change of two consecutive EOG traces stimulated by the same odorant pulse were │ΔV/V│=3.5 ± 0.9% (SE); │Δτr/τr│=2.2±0.7% (SE); │Δτd/τd│=3.9±0.9% (90 traces). The drift slopes estimated for the same records of repeated EOG recording were 0.8 ± 0.2% min-1 (10 consecutive traces, 200 s). Patch clamp amplifier performance was stable during the experiments with OE. The ramp-pulse experiments exhibited a linear dependency across the entire range of tested currents, and repeatability was found to be greater than 99%. The slew rate was smaller than10 μV/s, while the mean experimental rate of the EOG signal was on the order of 1,000 μV/s. The conditions of EOG experiments and the number of recorded EOG traces are mentioned in Table 1.
|
3.2. Kinetics of Responses to Odorant at Different Temperatures
- In the majority of cases, the isolated olfactory epithelia responded to a 0.25-second long pulse of odorant vapor by generating electronegative EOG responses that were synchronized with stimulus onset. Typical EOG responses at varying temperatures are illustrated in Figure 1 b. Differences were apparent in how olfactory epithelia responded at different temperatures. The maximal amplitude of the EOG dramatically decreased as temperatures increased from 20 to 34°C. The shape of the EOG curve also changes with a rise in temperature. The kinetic and thermodynamic analyses of EOG curves at different temperatures are given below.
3.3. Thermodynamic Analysis of EOG Recordings
- The EOG kinetic properties were used to calculate thermodynamic parameters (Ea, ΔH, ΔS, and ΔG). The processes of activation and deactivation of EOG were thought to be an overcoming a single apparent potential barrier. Therefore, the apparent thermodynamic parameters elucidate the entire process of EOG generation. The models describe the overall activation-deactivation processes. The thermodynamic parameters were obtained using four different methods: 1. Arrhenius and Eyring equations for various steady-state temperatures; 2. Arrhenius and Eyring equations for temperatures that change slowly from one temperature to another; 3. Arrhenius and Eyring equations related to the change of relative area under EOG peak for various steady-state temperatures; and 4. from the cumulative frequency distribution at two temperatures.
3.4. Arrhenius and Eyring equations
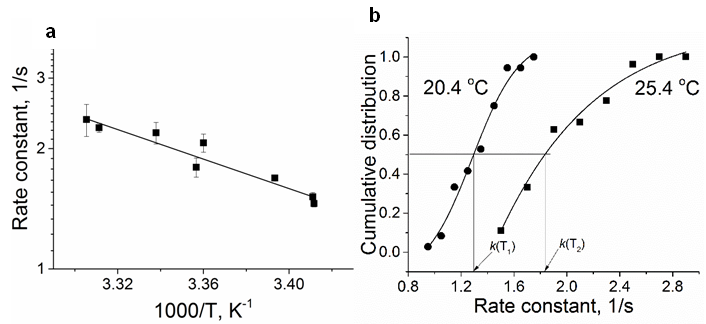
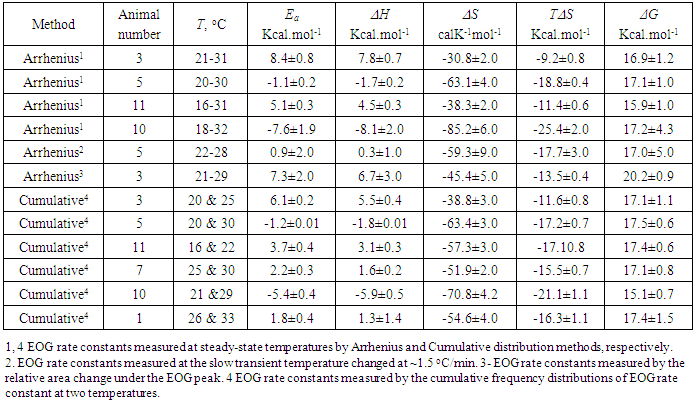
- Figure 2 a illustrates Arrhenius plot of experimental EOG recordings at steady state temperature in a range of 21-31°C for the rate constant. The example of calculating thermodynamic properties of EOG processes using Arrhenius and Eyring equations and experimental results are provided in the Supplementary information. The parameters of Ea, ΔH, ΔS, T ΔS, and ΔG for this experiment in addition to six more experiments using Arrhenius plot are illustrated in Table 2.
|
3.5. Cumulative Frequency Distributions of EOG Rate Constant at Two Temperatures
- Using Eqs (13-16) and (8), the apparent thermodynamic parameters Ea, ΔH, ΔS, T ΔS, and ΔG for the activation-deactivation can be calculated from the experimental data through the cumulative distribution function of the rate constant at two steady-state temperatures. Figure 2b illustrates the cumulative distribution function of the rate constant at two steady-state temperatures. Points are the rate constant times obtained by using frequency distribution of rate constant at temperatures of 20.4 and 25. 4°C. Based on the rate constant cumulative distributions, we have the values of k1=1.3 1/s and k2=1.8 1/s at temperatures T1=293.4 K and K2=298.4 K.The example of calculating the thermodynamic properties of EOG processes using cumulative frequency distributions of EOG rate constant at two temperatures from the experimental results are given in Supplementary information. The parameters of Ea, ΔH, ΔS, T ΔS, and ΔG for this experiment as well as for six more experiments are depicted in Table 2.
3.6. Thermodynamic Correlates of Activation-Deactivation of Olfactory Respond to the Odorant
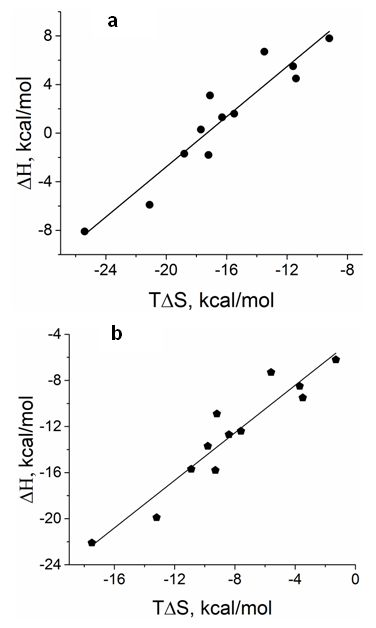
- When the enthalpy changes (ΔH) were plotted as a function of the energy of entropy contribution (TΔS) provided in Table 2, the data were fitted with a single line that corresponded to the equation ΔH= ΔGo+TΔS, where ΔGo=17.6 ±1.4 kcal/mol and slope =1.01±0.08 (Figure 3 a). The average values of thermodynamic parameters in Table 2 are as follows: Ea=1.7±1.4 (SE) kcal/mol; ΔH=1.1±1.4 (SE) kcal/mol; ΔS=-54.9±4.4 (SE) cal mol-1K-1; T ΔS=-16.2±1.3 (SE) kcal/mol; ΔG=17.2±0.3 (SE).kcal/mol.
4. Discussion
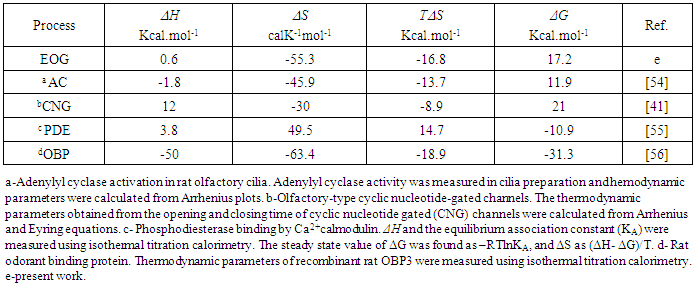
- In the majority of cases, the olfactory epithelium responded to 0.25 second long puffs of odorant by generating electronegative EOG responses that were synchronized with the delivery of stimulus. Typical EOG responses are shown in Fig 1 b. The shape and kinetics of EOG responses change with a rise in temperature. The mean time of half-rise (τr) decreased significantly at the level 0.05 from 225.4±6.2 (SE) ms to 184.1±1.3 (SE) ms when temperature increased from 16 to 20°C [F(1, 70)=354, p=0.0]. In a similar manner, the mean decay time (τd) decreased significantly from 529.1±20 (SE) ms to 416.4±3.6 (SE) ms at the same elevation of temperature (F(1, 66)=89, p=0.0].The thermodynamic EOG model shows a rather broad variation of enthalpy (ΔH) from 8.9 to – 8.1 kcal/mol, while the entropy contribution (TΔS) changes from -8.1 to -26.1 kcal/mol (Table 2). As evidenced in Figure 3 a, the change in enthalpy (ΔH) was compensated by a change in entropy contribution (TΔS), which allowed the change in Gibbs free energy (ΔG) =ΔH-TΔS to remain unchanged. This phenomenon called enthalpy-entropy compensation had been observed in the thermodynamics of several physical-chemical and biological processes [52, 53]. Notably, ΔG0 obtained from the enthalpy-entropy correlation plot is not significantly different from the average value of ΔG=17.2±0.3 (SE).kcal/mol that is found in 12 experiments, as shown in Figure 3 a. The positive and negative values of the change of enthalpy indicate that overall EOG processes could be endothermic or exothermic, whereas the change of entropy contribution was negative at the experimental conditions of our experiments. The change of the total EOG Gibbs free energy is positive, which indicates the exothermic process [46]. Enthalpy-entropy compensation was observed in other molecular recognition components involved in the olfactory transduction cascade (adenylyl cyclase, cyclic nucleotide-gated channels, and phosphodiesterase-Ca2+calmodulin). Importantly, the adenylyl cyclase activity was measured in cilia preparation by the radioactive assay [48-50]. The thermodynamic parameters calculated by Arrhenius and Eyring equations using the experimental adenylyl cyclase activity at 19.7 and 33°C showed ΔH=-1.8 kcal/mol and TΔS=-13.7 kcal/mol that compensated each other, which led to free energy of binding of 11.9 kcal/mol (Table 3).
|
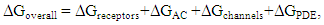 | (24) |
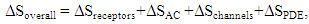 | (25) |
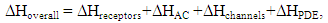 | (26) |
|
5. Conclusions
- 1. Amplitude and area under peak of electroolfactogram recorded in isolated rat olfactory epithelium are shown to reduce at elevated temperatures in the range of 16 – 35°C.2. The energy associated with the change of apparent entropy, TΔS, correlates with the change in apparent enthalpy, ΔH, keeping the apparent free energy ΔG= ΔH-TΔS constant.3. Thermodynamic enthalpy-entropy compensation in our experiments and those in literature is not found to be consistent with shape mechanism of olfaction.
ACKNOWLEDGEMENTS
- The work was funded by National Institute of Science and Technology (NIST) grant: 70 NANB14H324.
DISCLAIMER
- Certain commercial equipment, instruments, or materials are identified in this paper to specify the experimental procedure adequately. Such identification is not intended to imply recommendation or endorsement by the National Institute of Standards and Technology, nor is it intended to imply that the materials or equipment identified are necessarily the best available for the purpose.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML