1. Introduction: Finite-Element Method and the Theory of Transformations

Finite-element method (FEM) is the classical method of surface visualization in computer-aided design. This method is used both in CAD systems for geometric modeling and visualization and in CAE systems, which allow to analyze geometric parameters and dynamic properties of the model. FEM is also a good method for physical investigation of a geometric model. Finite-element method is traditionally used in the area of heat and mass transfer, hydrodynamics and fluid mechanics, vibration analysis, stress and strain modeling, electrostatic potential and magnetic field distribution analysis, etc[1]. In solving the inverse problem this enables to represent the form of the real object as a product of its perturbation by external influences, allowing, however, to predict the state of an object under various external influences.

The resulting grid is essentially a discrete approximation of geometry of the initial object.

In the classical FEM h-version polynomials of fixed degree are used as the function of shape and the precision in this case is achieved by means of increasing the sampling by reducing the size of cells. In contrast, the p-version of the method uses a fixed grid, and the accuracy increases with increasing of the degree of the function of shape. A simple example of a finite element mesh is a Cartesian coordinate system, based on linear square cells, which approximates the plane.

Such a distorted mesh can also be considered as a Bezier surface determined by the polygon of a tetragonal type. Linking of the corners of such cells forms a bilinear surface, and the boundary curves, which together describe the surface, form patches: Ferguson patches, or F-patches, when zero torsion vectors, bicubic patches in general case and Coon's patches in the boundary case). If the boundary curves of the surface are Bezier curves, the corresponding conjugation of Bezier surfaces can be considered as a set of Bezier patches. In this case the finite elements (cells) are patches themselves, therefore they are identical to the regularized areas in one of the branches of FEM - the so-called mapped element approach at transfinite or isoparametric mapping. Transfinite mapping allows the mapping of four-sided areas on regularized area, so any point at the boundary of the initial area appears on the boundary of a regularized area. Isoparametric mapping as a special case of transfinite mapping with a quadratic or cubic transformation (i.e., with the use of quadratic or cubic interpolation functions) allows to use a finite number of projections in visualization. In this case, visualization of deformable surfaces by means of FEM, and using Bezier meshes can be considered equal.

In accordance with the D'Arcy Thompson’s transformation theory[2], the morphological evolution of biological systems can be visualized as a deformation process of the Cartesian (rectangular) coordinate system of an initial organism, considered as a reference configuration. As a rule, the geometric morphology uses another instance or the average configuration of the taxonomically related species as a reference. This approach allows us to study the deformation of the transformation lattice (tangential space) relative to the reference configuration (relative warps), taken as an undeformed system, because morphological objects are comparable only in the case of correlating them with the same tangential or Kendall space[3]. Therefore it is required to use the same reference configuration for all objects of the sample. In the CAD terminology this means the use of a grid based approach, based on the transformation of a coordinate lattice into the mesh during the transformation of mesh cells into finite elements, deformable under the influence of external forces (the so-called displacement-based formation).

However, if the formation of biomorphs in the course of evolution can be explained by a deformation of some space, then for the phylogeny it is important to choose the criteria for selecting an object whose shape can be associated as initial undeformed space (Cartesian coordinates). Obviously, if the choice of the initial phase is arbitrary, its appearance can also be explained by the deformation of a transformation grid of the previous state (and so on until protobiological systems). The arbitrariness of the reference point makes unknowable the causal relationship between the stages, matched with the original and derivative transformation grids, since the possibility of each subsequent object for null object, makes the connectivity of operations, corresponding to series of deformations of coordinate systems lost. In essence, the difference between real phylogenetic transformations and the imaging model abstraction, which allows a comparison of the orthogonal lattice to any biomorphs, is like the difference between Markovian and non-Markovian processes. The real morphology depends on the sequence of preceding transformation lattices and the abstract model is a consequence of a distortion of a single conventionally mapped to a rectangular coordinate system. As mentioned in[4], the choice of the initial organism (reference) in the transformation theory is arbitrary.

Obviously, the nature of its changes depends on environmental conditions and it is formed during the phylogenetic process. Physical agents, "distorting" the mesh, in this case are the impacts that, according to[1], can be studied and simulated using FEM-systems. Therefore theoretically it is possible to simulate a phylogenetic process from abiogenesis to higher stages using FEM as modernized version of D'Arcy-Thompson meshes, which possesses the ability to identify the deforming factors and prognostic significance. In the standard interpretation of the theory of transformations any change in shape is formally regarded as a mechanical process. This fact can be confirmed by the similarity of works on the theory of transformations and deformation of tensile elastomers[5], the method of deformed plates[6] and models of pulsed deformation[7]. However, all the authors failed to describe the nature of the impact that triggered these obvious (in a mechanical approach) strains.

Since 60-ies the nature of inductor in the works on the theory of transformation hasn’t been seriously considered (for simulation purposes). R. Rosen, one of the leading specialists in this area, introduced fundamental amendments, which led to the reconciliation of the theory of transformation and the theory of optimality and replacement of the inductor problem with the indication of the optimal structure of an organism[8]. Evidently, the optimal structure is the result of both virtues of environmental factors and the own physical properties of the organism, so such an elementary reduction does not answer the main question. Subsequently, there were attempts to consider embryogenesis as epigenetic process (i.e., controlled by the environment) and to describe epigenetics as a mover - the driving force and initiator of the structure plan[9]. This approach also does not answer the question about the nature of the influence, as well as the previous method of reduction and hence can not be considered satisfactory because of the idealistic nature of the conclusion.

Thus, one should first answer the question: which factor initiates transformations and how does mover influence a grid of finite elements?

The method of solving this problem is very important for scientific visualization of the phylogenetic process: what should be simulated and visualized - just CAD geometric shape with arbitrary virtual surface perturbations or CAE-system, in which all tolerances are constructively justified, and the deformations, which are results of the objective effects, can be easily studied by modeling these effects using FEM?

In fact, there is no reason for abandoning the existing approaches. They only require specification, i.e. giving a real physical content to the abstract factors. For example, in[10] it’s postulated that deformed transformation grids (tangential space) can be regarded as a mapping of an acting factor - so-called Formative Field, and in[11] it was shown that any change is a product of the agent activity (agent-based), and the forming relief is an epigenetic landscape by Rene Thom. It is known that the field concept is widely used in physics and technology, and the range of phenomenon studied using FEM may also be considered as "fields" (hydrodynamic fields, thermal fields, the velocity field, stress field, strain field, magnetic field, the field of central forces, the optical field, mass transfer of the field - it is just a standard special terminology). The effects of this kind may be the reasons and the model-visualized factors of D'Arcy-Thompson’s grids’ transformation from the planar surface to highly differentiated three-dimensional structures.

If we start from abiogenetic and evolutionary assumptions, it is advisable to take for the unperturbed (planar) grid a structureless (at the used sampling level) sample, and then its directed perturbations can be considered as structuring.

In this case the problem of distorted transformation meshes should be considered as a problem of analytic approximation of a real biological objects’ shape using them. As it was mentioned above, the essence of the finite element method is an approximation of the object’s geometry by a corresponding mesh. There are the following directions in this approach:

1. Identification of the distorting effect waveform through the previous system state and the output signal - its subsequent state,

2. Explanation of the formation mechanisms of an existing form as a product of the preceding form, based on the selection of the optimum signal, ensuring the structurization,

3. Description of the fossil forms’ deformation on the basis of morphology of both the earlier and the later residues, as well as conditions of their occurrence,

4. Predicting the deformation of the object from the known possible deformation signals and the shape of the object (in the long-term prediction - from the trends of transformation grids’ deformation). In essence, the use of a single initial planar system, coupled with an objective "zero"-structure, solves the problem of the original transfer function of the black box in this system.

Since the transformation mesh without distortions corresponds to steady state in which no self-organizing structures occur, one can assume that this state corresponds to abiogenic period. In this case, the specific distortion of the transformation grid in abiogenesis, caused by external influences, can be interpreted as the emergence and development of precellular structures. Using various types of input signal (effects), one can get the corresponding output deformations of the coordinate grid. Consequently, it is possible to simulate the forms of protobionts using input signals, corresponding in form to the main abiogenetic factors. However, it makes possible the solution of the inverse problem: reconstruction of perturbation forms through the morphology of protobiological systems, formed under their influence. This approach is discussed in detail in the experimental section of this paper.

2. From Simulation of Transformations to Engineering of Biological Forms

The possibility of the distortion modeling of the transformation grid under the influence of a given input signal is a prerequisite for computer-aided engineering of biomorphs using the input effects with a programmed form. Knowing the structure of the inducing impact and the response of the system, one can control the response of the system and, consequently, form a system with pre-defined morphological characteristics. In[12] a method of computer morphometry (Computer-Aided Morphological Analysis - CAMA) is described, which uses the algorithms of the transformation theory and allows investigating the structure of distortions and the distorting effects. Profile information (topography) of the transformation grid surface, obtained via morphometric operations, can be used in a search of ways of acting on the intact (undeformed) transformational grid in order to reach a similar morphometric result.

For such a kind of modeling it is advisable to use the capture of transformation grid profile (reading of morphometric data while image processing of biological objects in real time) and its software visualized distortion. Later one should implement this distortion in a real model, and then compare the results of the distortion in experiment and in the model. In[13] the applicability of the Arcy Thompson’s approach for biomorphic systems in computer design is mentioned. This means the possibility of computer design (CAD) and visualization of biological models, implemented physically (abiogenically). Any biomorphic system, by definition, is a biomimetic one in terms of distortions. Since in this aspect we are only interested in the similarity of morphological characteristics of the transformational grid, this condition is necessary and sufficient for this case. In[14] proposed the use of D'Arcy-Thompson’s transformation grids for geometrical and morphological optimization of biomimetic structures similar to biological systems. This allows the construction of such microobjects, based on computer simulation data. A similar approach for macroscopic objects is considered in[15].

The choice of the scale of simulation, however, is important because it is tantamount to the question of choosing the accuracy of the finite element mesh, i.e. the sampling of the method. If at a nonuniform non-isometric change of the transformation grid the squares of distorted rectangles, which are the former cells of the coordinate mesh, are different, then the discretization of structures, which centroids are located in them, changes in the grid unevenly - depending on the amplitude of relative deformations. As a consequence, a number of structures can be out of resolution and, therefore, not subjected to adequate transformation.

Consider an example from the related area - decomposition method of morphometry. Assume that there is a micro-object (coacervate drop) to be decomposed into squares using the so-called quadtree decomposition algorithm, that is, in essence, a synthesis of a "transformation grid" adequate to the hierarchy of approximated image components invested in it. Then the number of resolved components of the image (see fig.1a) will correlate with their hierarchical position, and consequently, at low resolution the shape of the object will be unobservable (fig. 1c), and with excess resolution the forming elements will be merged into a single array (fig. 1d). Strictly speaking, with a maximum resolution threshold the system is indistinguishable from a homogeneous medium, and at a minimum one it can’t be determined as an organized biological structure. Therefore, to avoid the reduction in resolution of this method, it makes sense to define the limits of applicability of the renormalization-group approach to the transformation grids of such a kind. In the case of automatic mesh generation (fully automatic mash generation), this problem escalates.

Figure 1. Decomposition of a microscopic image (MATLAB): a - original image, b – the optimal resolution, c - low resolution of the microscope, d – excessive resolution

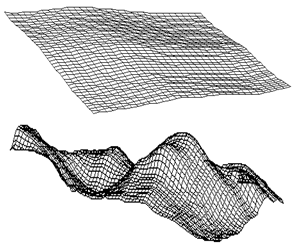Figure 2. A structured plot with a small (top) and large (bottom) magnification. The top transformation grid has a lower absolute discretization than the bottom one

Fig. 2 shows two fragments of transformation grids of the sample structure, registered by the standard method using 3D-Doctor (v. 4, Able Software Corp.). The mesh generation was carried out in fully automated mode. The top image registration was carried out at low magnification of the initial image (computer was switched with the camera fixed in the tube of a trinocular microscope); the bottom image registration was made at increased several times program magnification. One can see that on the bottom image there are some relief items identified, which could not be seen on the top image. However, at the excessive increase comparable to the matrix noise, a small fragment of the bottom picture shows the appearance of fluctuations, which are not related to the structure (microstructure) of the sample and changes in its shape and surface. An example of such an obvious phenomenon may be seen at the schedule shown in fig. 3.

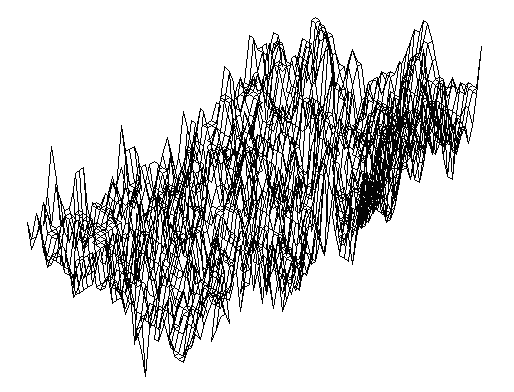Figure 3. The noise fluctuations in a transformation grid

It is clear that the level of sampling should be compared with the size of ultrastructural units of the cell (in the case of cellular systems), determining the structure of a transformation FEM-mesh. Only under this condition the recorded signal can be used for acting the transformation grid and its directed deformation (the selection of scaling is required as a replacement of signal filtering).

What are the initial media for digital and physical modeling of deformations, adequate to deformations of primary biological structures? From the previous paragraph, one can conclude that they should be cell models¹. In[16] the applicability of D'Arcy Thompson’s theory to such systems ("Soap Bubbles") is proved, that correlates with the Oparin's coacervate hypothesis. The application of this method to modeling of bone and the like reticulum («super-lattice») structures is stated. However, there is made an important reduction of biological structures (animate) of this type to non-living (inanimate) structures such as foam & soap bubbles, as in the aspect of modeling and visualization subject to the condition of isomorphism they are indistinguishable. The work[16] also shows the relationship between crystal structures and membranes of cellular systems of apension type - so-called Closed Cell Structures Foam, from the viewpoint of transformation theory and visualization of cellular structures. In his simulations the author of[16] relies on the reproducibility of the transformation grid deformations in cell membranes’ dynamics (compare with[5]) and in crystal structures (compare with[6]), introducing a special computer-visualized model based on these principles (a model of the crystallized structures or membranes which emerge from cellular aggregation through simulation of analogue models). Thus, to simulate the deformations, leading to the morphological evolution of the simplest biological structures it is appropriate to use artificial cells.

Artificial cells are synthesized on the basis of membrane vesicles, as a rule, according to known methods, proposed by Chang[17] and accessible now to any biophysical laboratory. Therefore, FEM application to such structures (especially with the introduction of deterministic factors and transition to FEM at the stage of design) is rather possible. There are known different methods of synthesis of artificial cells both on organic[18-20] and inorganic[21] basis². They have already been simulated using Turing’s mechanisms of morphogenesis in biological systems. That certainly makes this method a subject of the theory of transformations, which simulates similar phenomena in the course of evolution and ontogeny)[22,23]. In this works visualization of the mesh deformations was carried out using spline interpolation and decomposition analysis, that are widely used since the classical works of Bookstain in geometric morphometrics and the theory of transformations[24] (on the application of splines in these areas, see also[25]). Meanwhile, in[26] concentration waves, described according to Turing’s interpretation as initiators of morphogenesis, are considered as transformation grid deforming agents, whereas in the Encyclopedia of Nonlinear Science[27] Turing’s approaches (cellular automata based on reaction with diffusion, vawe processes and dissipative patterns) and D'Arcy-Thompson’s theory are considered as equal and complementary. Thus, one of the first simulated deformations is the surface oscillation. The applicability of this approach to inorganic artificial cells is confirmed by the fact that Achim Müller, who first proposed the method for synthesis of inorganic "artificial cells", in his primary work[28] also based his theoretical foundation on the theory of transformations when considering the properties of the molecular frame of "artificial cells’" capsules.

The conditions under which deformation of transformation grids occurs can be grouped into three basic groups:

I. Deformations associated with the growth of the organism (either Gaussian uniform growth[29] or development, in which the similarity transformation is not satisfied). For biomimetic systems, in particular, artificial cells, this condition is valid in the presence of adaptive growth as a consequence of metabolic processes[30]. These phenomena occur in artificial cells, synthesized via modern techniques.

II. Deformations associated with movement (locomotion) of the organism. For example, in[31] transformation theory is applied for description of moving fibroblasts on elastic substrates, and in[32] - for description of the deformations (extension or retraction) of moving cells (as a result of polymerization of motor proteins - actin and myosin). Also there are some works, comparing the movement and morphogenesis or the formation of colonies (by forced and motion) from the viewpoint of transformation theory[33], as well as works that connect molecular mechanisms of locomotion with the morphological evolution[34] ( which are also based on D'Arcy-Thompson’s theory). Thus, the movement of cells (or artificial cells) can be considered as a simulated criterion of their potential morphological evolution. According to[35], the similarity of the organisms’ dynamics indicates a relative nature of their transformation grids. In other words, if artificial cells reproduce in the course of experiment the dynamics of transformation grids, which was model-predicted for biological cells of the natural origin, they can be regarded (ad hoc) as adequate cytophysiological cell models in an evolutionary plan. According to[36], motion deformations (deformotion - from deforming motion) can be used for image segmentation in visualization of locomotor dynamics of the objects. In this connection it is possible to identify rigid structures in organisms via the principles of mathematical morphometry and the theory of transformations[37].

III. Deformations associated with biomineralization and fossilization. Thus, in classical monographs[38,39] on paleontological systematics and taxonomy of fossil the nature of transformational grids’ changes is regarded as the guiding criteria for classification of the remains. On the other hand, the process of biomineralization (matrix synthesis according to the biological prototype), from the viewpoint of transformation theory can be interpreted as morphosynthethis of biomimetic structures[40]. Moreover in transformation theory it is not essential which object is the primary one, and which - the secondary one (respectively - primary and secondary transformation grids). A well-known work[41] indicates the connection between biomimetic structures in non-living nature, and biomineralization, that is a consequent to reproduce such structures and phenomena in the laboratory (from Reading to Writing). This phase should be preceded by a stage of numerical simulation and computational modeling. The same approach, in particular, is implemented in this paper. From designing standpoint, formation of artificial systems that mimic the structure and functions of living cells, is justified by the reproducibility of their transformation FEM-grids - both in theory and in practice[42].

Thus, the methods for modeling of the mentioned deformation types could also be divided into three groups: the distortion of the grid without surface area conservation (for the phase space - the case of non-Hamiltonian systems) and the volume of the model object – an organism; the grid distortion with nonconservation of the object localization (shift invariance); static distortion of the grid. For the first two cases it is useful to reproduce the dynamics of deformation and to compare the simulation results with time-lapse photoregistration or rapid shooting, as it was shown in this paper. Initially as a deformable data array one can use 3D-confocal microscope images or digital micrographs of prototype objects. For the first time such a method was applied in biomedical genetics in the study of mutations, deforming soft tissues of the frontal part of the face[43] (it's the first application of the transformation theory in the modeling of genetic effects, except for[44]). Since every stationary deformation can be described using mathematical tools of catastrophe theory[45], "inherited" and "unheritable" parameters in the model can be detected only mathematically (the existence of the so-called memory of dangerous bifurcations, leading to the system transfer into a self-sustaining mode, stabilizes the structure of space states, which replaces the function of maintaining genetic structure in non-genetic models). In this regard it’s possible to realise the model of inherited transformations visualized by using the above set of mathematical approaches.

3. Experimental Section: Direct Detection of Transformation Grids in the Model of Abiogenesis

In[46] it has been shown that biomimetic oscillatory reactions, accompanied by photoinduced cellular pattern formation, may be considered as a model of abiogenesis (and protobionts’ morphogenesis). The formation of "artificial cells" in the course of such processes can be described and simulated using the FEM-method or Bezier surfaces as a tool of the theory of transformations. The original process that occurs in a liquid crystal medium, leads to the formation of convective rolls in it, providing heat and mass transfer in the system. Such structures at an early stage can be detected by a digital system of contact gel-documentation, which imports data to a computer for the purposes of their frther visualization and analysis (a scheme of such sistem is shown in fig. 4). During visualization these structures are identified as parallel formations of the wave nature (fig. 5), which subsequently form standing waves and wave packets shown in fig. 6, 7. These wave structures underlie the formation of dissipative biomimetic systems (micrographs of the latter are given in fig. 8).

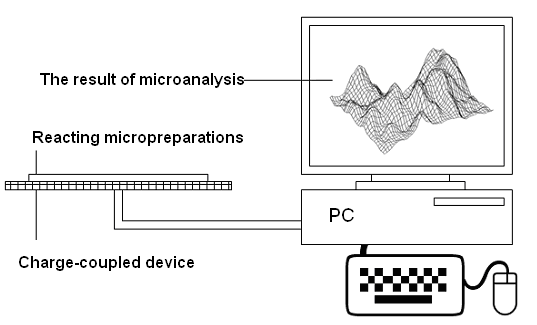Figure 4. A setup for gel-documentation of oscillatory reactions in active partially ordered reaction-diffusion media

Figure 5. Convective rolls in the initial irradiated medium

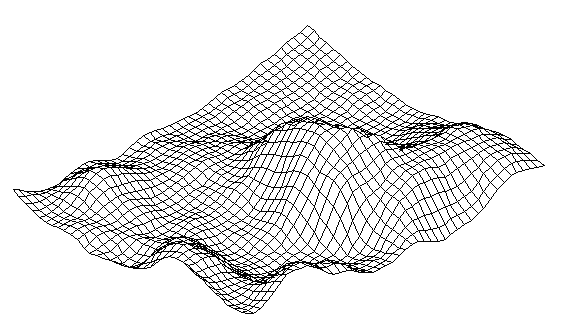Figure 6. A single standing wave in a reaction-diffusion system

Figure 7. Stationary wave structures in a self-organizing medium

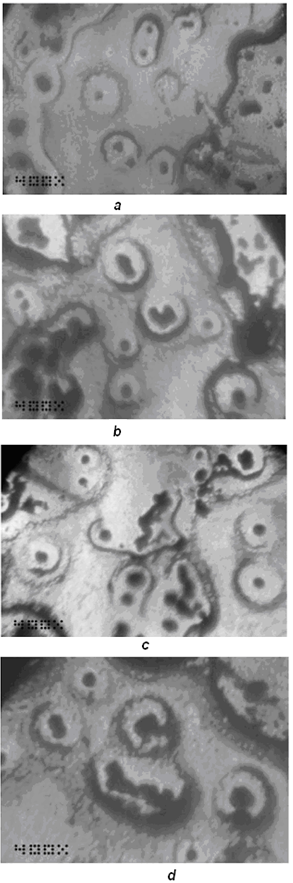Figure 8. Self-replicating dissipative structures formed as a result of perturbations of a transformation grid (from[47])

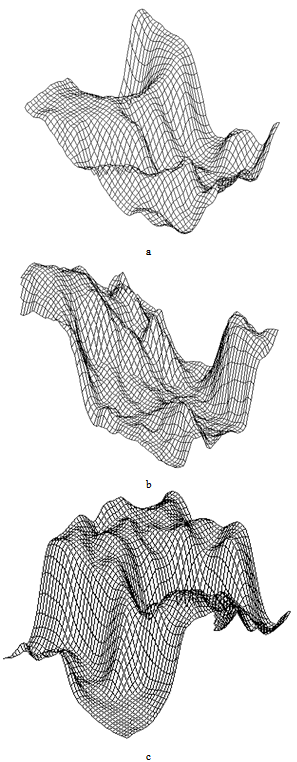Figure 9. 3D-disturbances of the grid occur due to the growth of “pedestal” (background) and collective processes in active medium

From the non-linear physical positions, single standing waves have the form of intensity distribution in a rational “soliton” with increasing localized perturbations (explode-decay solitary wave)[48] that can be seen in fig. 6. On the other hand, it is obvious that the superposition of different vibrational modes can lead to the formation of "solitons on pedestal", considered as nonlinear superpositions of a soliton and a constant background (that leads to the beat generation between it and the background). The surface schedule in fig. 7, for example, has similar properties. Also in the case of efficient pumping of the medium one can observe the growth of a pedestal (background), accompanied by the release and visualization of three-dimensional structures that are the products of self-organization of biomimetic (biomorphic) systems in active medium. An example of such process is shown in fig. 9. One can see that the emerging structures increase the amplitude, for the most part, due to the growth of a pedestal. This effect corresponds to the process of phase separation in the system, which is accompanied by the particle aggregation and separation of the fronts of mass transfer. These phenomena lead to the emergence of clear boundaries between the self-organizing bands and their environment. Thus, in particular, the appearance of rolls and membrane structures in a heterogeneous (ultradispersed) active medium was observed[46].

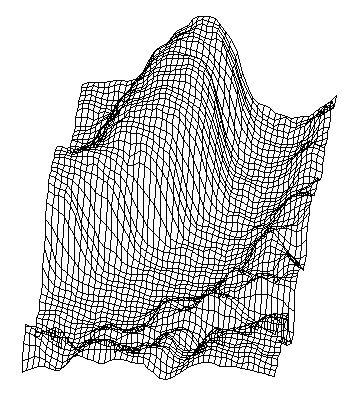Figure 10. Formation of a membrane shaft in a self-organizing system

An example of membrane structures’ emergence due to the aforesaid process is shown in fig. 10. However, the forms of single aggregating structures registered inside locked-in membranous structures are also identified as grid deformations of a quasi-periodic character (see fig. 11). A similar picture can be observed during visualization of modulation instability of perturbations in solutions of nonlinear equations[48]. In developmental biology such quasi-periodic structures take place at the segmented growth (or metamerism) and are usually described by the theory of transformations[50]. Formation of membrane structures, which are responsible for compartmentalization in biological systems, (that is, in essence, the morphogenesis of the cell) can be considered (in the case of simulation of abiogenesis with dissipative structures) as a prerequisite for interpretation of such structures as model analogs of prebiological structures (protobionts). This interpretation becomes more reasonable because autosolitons, or dissipative solitons, are the models of morphogenesis of biological structures. The work[49] shows the possibility of solitons’ formation in biochemical processes, and postulates that "the objects at each biological level - cells, organs and animals - can be considered as dissipative solitons".

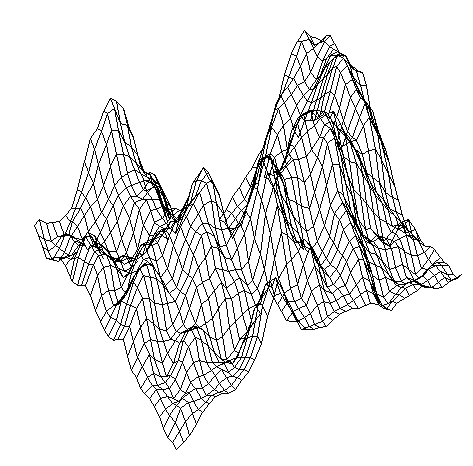Figure 11. Modulational instability in a self-organizing system

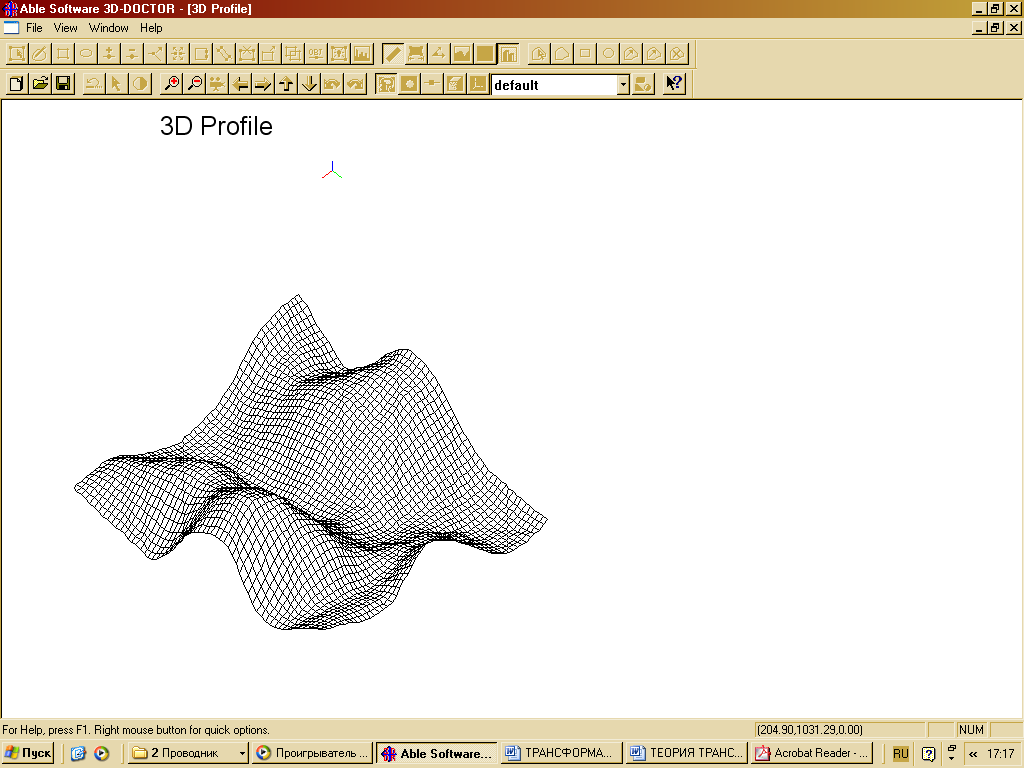Figure 12. Interaction between “solitons”, which differ in amplitude and phase. A quasiperiodic system

Assume that the inductors of morphogenetic processes in primordial soup were the same as radiation sources that caused self-organization of protobiological structures[50-56]. The simplest deformation associated with the passage of radiation in condensed matter is distortion. There are known basic algorithms for MATLAB, which allow simulating the radial distortion (Radial Pin Cushion Transform):

xt = xi(:) - imid;

yt = yi(:) - imid;

[theta,r] = cart2pol(xt,yt);

a = -.0005;

s = r + a*r.^3;

[ut,vt] = pol2cart(theta,s);

u = reshape(ut,size(xi)) + imid;

v = reshape(vt,size(yi)) + imid;

tmap_B = cat(3,u,v);

I_pin = tformarray(I,[],resamp, [2 1], [1 2], [],tmap_B,.3);

subplot(339)

imshow(I_pin)

title('pin cushion')

For barrel distortion (Barrel Transform to Distortion)the algorithm is as follows:

xt = xi(:) - imid;

yt = yi(:) - imid;

[theta,r] = cart2pol(xt,yt);

a = .001;

s = r + a*r.^3;

[ut,vt] = pol2cart(theta,s);

u = reshape(ut,size(xi)) + imid;

v = reshape(vt,size(yi)) + imid;

tmap_B = cat(3,u,v);

I_barrel = tformarray(I, [],resamp, [2 1], [1 2], [],tmap_B,.3);

subplot(338)

imshow(I_barrel)

title('barrel')

(with amplitude-varying values of a in cubic terms).

Figure 13. Prosenchymal deformation simulation via distortion

Those algorithms allow to deform the meshes of cells’ or artificial cells’ micrographs, varying the parenchymal³ coefficients and, therefore, the habit of cellular structures. It is also possible to simulate spherocytosis (in a physical model of artificial cells it was described in[57]), anaboly, elliptocytosis, anisocytosis and some other membranopaty.

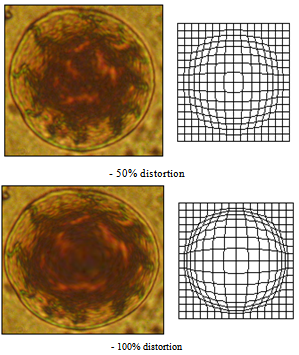Figure 14. Barrel distortion - simulation of anaboly and spherocytosis

Fig. 13 shows examples of transformation grid distortion using Radial Pin Cushion Transform and their corresponding forms of distortion of original artificial cells. A micrograph of the same deformation in a real artificial cell is given in Fig. 15 (a): such structures occur in the medium under certain conditions of cultivation. In the opposite conditions of cultivation and distortion simulation or after applying the algorithm of barrel distortion anaboly and spherocytosis of artificial cells can be observed. An example of distortion simulation is given in fig. 16, and its experimental analog – in fig. 15 (b)⁴. One can observe a clear anisocytosis in the system because artificial cells have different shape and volume.

The imposition of deformations is also possible, when the result of the previous modification becomes a starting point for the following distortion. Thus, the subsequent imposition of oscillatory-type deformations on a prosenchymal cell leads to the formation of large-scale wave-like distortions on its surface. Examples of such structures in the model and experiment are shown in fig. 16.

In this case, it makes sense to inverse the problem: which deformation has led to the formation of specific forms observed, and particularly to the form of a primary eukaryotic cell? According to the experiment, formation of the central granule in artificial cells occurs due to self-focusing of optical beams in them or via photoinduced reactions, accompanied with the formation of optically-dense centers (hot spots), shown in fig. 17 (3D interference surface analysis).

Figure 15. The results of experimental distortion in artificial cells: a – elongation, b - anaboly and anisocytosis

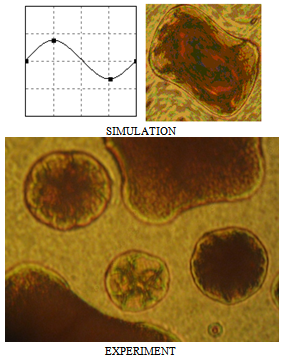Figure 16. Imposition of wave disturbances on a transformation grid

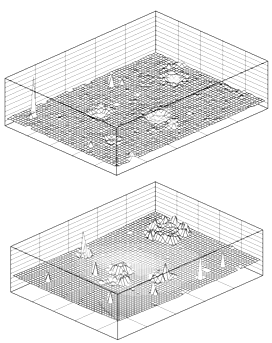Figure 17. Visualization of “hot points” (the areas of self-focusing) in a photochemical system by an interferometric imaging technique

Consideration of self-focusing as self-organization is a matter of simple terminology. If you add dissipative terms in Schrödinger equation, a stable structure arises. If we impose it on a complex function with non-real coefficients, it will cause damping or instability depending on the sign. In the complex case this leads to Ginsburg-Landau equation. In two-dimensional Schrödinger equation there are no stable structures, and if we add a nonlinear imaginary part to the damping, a collapse will arise and disappear there, while in 3D-case special structures will occur - the so-called "long-living focuses."

Self-focusing effect, coupled with the emergence of a standing wave can be simulated with specialized software. Thus, the listing for Pascal looks like this:

c3:=cos(ga);s3:=sin(ga);

ux:=abs(b-a)/(nx-1);uy:=abs(d-c)/(ny-1);

x:=a;y:=c;z:=f(x,y);

xx [1,1]:=x*c1+y*c2+z*c3;

yy [1,1]:=x*s1+y*s2+z*s3;

xmin:=xx [1,1];xmax:=xmin;

ymin:=yy [1,1];ymax:=ymin;

for i:=1 to nx do

begin

y:=c;

for j:=1 to ny do

begin

z:=f(x,y);

xx [i,j]:=x*c1+y*c2+z*c3;

yy [i,j]:=x*s1+y*s2+z*s3;

if xmin>xx [i,j] then xmin:=xx [i,j]

else if xmaxif ymin>yy [i,j] then ymin:=yy [i,j]

else if ymaxy:=y+uy;

end;

x:=x+ux;

end;

setcolor(tt);

ux:=(xmax-xmin)/(getmaxx-200);

uy:=(ymax-ymin)/(getmaxy-200);

dy:=getmaxy-100;

for i:=1 to nx do

begin

moveto (round((xx [i,1] -xmin)/ux), dy-round((yy [i,1]-ymin)/uy));

for j:=2 to ny do

lineto(round ((xx [i,j] -xmin)/ux), dy-round((yy [i,j]-ymin)/uy));

end;

for j:=1 to ny do

begin

moveto (round((xx [1,j] -xmin)/ux), dy-round((yy [1,j]-ymin)/uy));

for i:=1 to nx do

lineto (round((xx [i,j] -xmin)/ux), dy-round((yy [i,j] -ymin)/uy));

end;

end;

begin

init_graph;

t:=0;

repeat

anim(12);

anim(0);

t:=t+1/100;

until keypressed;

closegraph;

end.

This algorithm leads to symmetric solutions, which simulate the channels formation, similarly as shown in Fig. 18. Visualization of concentric morphogenetic perturbations in the system under irradiation and the results of the centripetal concentration (nucleation) are partially shown in Fig. 19. Thus, morphogenesis of protobiological structures in the elementary case can be simulated using D'Arcy Thompson’s grid deformations under environmental factors.

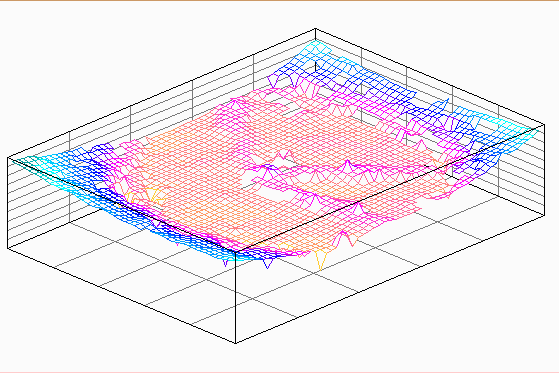Figure 18. The initial sample according to 3D surface analysis

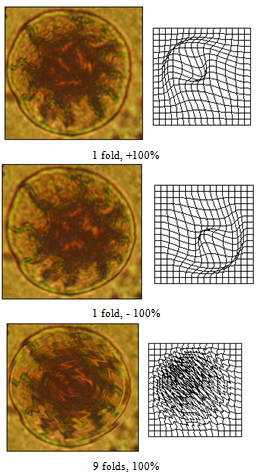Figure 19 (a). Formation of internal structures using grid perturbations

Resume

Total, in this paper:

1) A new modification of accepted morphological imaging methods based on grids for morphogenesis & abiogenesis description was proposed.

2) Its applicability not only in comparative morphologically, evolutionary and systematic studies, but also in abiogenetic research in shown.

3) It was suggested a new approach of deterministic or directed grid transformations, which allows to control the outcome of the process according to its trend.

4) A transition was made from a purely geometric simulation («CAD») to the analysis of the structure of distorting factors «CAE».

5) A new method for registration of the lattice deformation was proposed with its subsequent imposition during computer engineering of biomimetic structures.

6) The study identified a number of restrictions on scaling and sampling of the initial signal in D'Arcy Thompson’s transformation theory.

7) The paper describes a new system for gel documentation of reaction-diffusion processes that mimic morphogenesis in partially ordered media. The developed system outputs the data to a PC for 3D-visualization of the transformation grid perturbations.

8) The above method detected nonlinear pulses, waves and flows in active medium in the course of photoinduced self-assembly of artificial cells.

9) A method of predicting the likely distortions of primary artificial cells based on the methods of computer optics is developed.

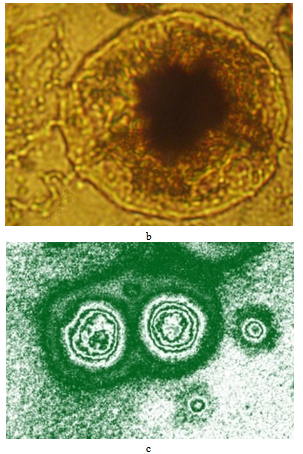Figure 20 (b,c). Vesicles with “nuclei”, obtained under experimental conditions: b – photomicrograph, c – moiregram (gradient map)

Notes

1. This follows from the phylogenetic assumptions: biological evolution in the early stages led to more complex single-celled forms, and then - the emergence of multicellular structures based on them.

2. In the present study, we used inorganic "artificial cells" as the most simple and available model objects.

3. The ratio of transverse and longitudinal sections. If the cell is elongated in length, it is considered as prosenchymal, and if it is oriented along the axes isodiametrically (or close to it), it is considered as parenchymal.

4. Three-dimensional reconstruction from interference microscopy data.