Abebe Belay
Physics Department, School of Natural Sciences, Adama Science and Technology University, P.O.Box 1888, Adama, Ethiopia
Correspondence to: Abebe Belay, Physics Department, School of Natural Sciences, Adama Science and Technology University, P.O.Box 1888, Adama, Ethiopia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The concentration dependent self-association of caffeic acid and its complexation with sodium ions have been studied in aqueous solutions at room temperature or 298 K. The self-association and hetero-association have determined by dimer model and Benesi-Hildebrand approach respectively. The dimerzation constants of caffeic acid in water and acetonitrile solutions are 2947 and 758 M-1 respectively. The equilibrium constant for the complexation of caffeic acid with sodium ions at the wavelength of 343 nm was 6860 M-1. The thermodynamic properties of self-association of caffeic acid were estimated from Van’t Hoff’s equation. The values of change in Gibb’s free energy, enthalpy and entropy are calculated at temperature of 328 K. The dimerization of caffeic acid are due to intermolecular hydrogen bonding by carboxylic acid groups of the compound and exothermic which characterize by relatively large negative of change in enthalpy. The intermolecular hydrogen bonding of such kind of compound is very important force in the formation of supramolecular liquid crystals.
Keywords:
Dimer Model, Benesi-Hildebrand Approach, Caffeic Acid, Thermodynamic Parameters, Non-Linear Curve Fitting
1. Introduction
Caffeic acid, trans-3- (3, 4-dihydroxycinnamic acid) prophenic acid is one of the most common phenolic acids frequently occurred in fruits, vegetables, cereals, legumes and in beverage of plant such as wine, tea and coffee for human consumption as simple esters with quinic acid[1-2]. The compound has attracted attention of researchers due to health promoting attributes, such as lowering the risks of cardiovascular disease, cancer, diabetes, and other conditions associated with aging. The biological mechanisms behind these effects are protection against free radicals, free radical mediated, inflammation and viral infection[1-3]. Caffeic acid is a multifunctional naturally available organic acid substance which plays a significant role in binding metal ions from natural environment, food substances and beverage such as coca cola, mineral water etc . The ligand has two complexing sites in competition: the catechol group (dihydroxybenzene) and the carboxylic function. Several coworkers have reported the complexation of this compound with different metal ions in aqueous solutions, Al (III)[4-6], copper (II), Ni (II), Zn (II) and Co (II)[6] and iron (III)[7]. In addition, the complexation of caffeic acid with polyphenol and aromatic compounds were also investigated by spectroscopic and computational methods to design advanced and controllable carriers of drugs and food components[8-9]. The investigation of self-associated molecules by spectrophotometric has a limitation due to difficulty in obtaining the spectra of highly concentrated solutions and the technique needs of careful observation of changes in the apparent molar absorptivity over a wide range of concentrations[10]. The formation of dimer complicated the use of Beer-Lambrt’slaw. The values of molar absorptivity and shape of the absorption band of the fraction of dimerized molecules are usually unknown and that often leads to difficulty in the interpretation of experiment[11]. Investigation of the self-association and hetero-association of the solute is an important phenomenon. This is accounted in analyzing and interpreting the spectroscopy, photophysics and photochemistry of the system[10-11]. Moreover, in order to design a more advanced and controllable carries of drugs or food components it is necessary to know the association mechanisms to control the processes. Despite, there were various research reports on the complexation of caffeic acid with toxic metal ions and other molecular compounds; however, currently there are no report as far as the author knowledge concerns on the concentration dependent self-association of caffeic acid, its thermodynamic properties and the complexation this compound with sodium ions, Therefore, the objectives of this research are investigating the self-association, hetero-association and thermodynamic properties of caffeic acid using spectrophotometric. The technique is the most suitable for quantitative study of the aggregation properties of the molecules as a function of concentration.
2. Materials and Methods
The studied compound in this work is caffeic acid, bought from Sgima-Aldrich. The absorption spectra were recorded by Perkin-Elmer Lamda 19 spectrophotometer with double monochromator, which offers the advantage of a low level of stray light that is significant for measure of high value of absorbance using 1 cm cuvette. The spectra were recorded with a spectral band width of 2 nm and scan speed 240 nm min-1. The acquisition of data were performed by 4.3 UVCSS soft ware, using a suitable computer on line with the spectrophotometer. The electronic absorption spectrum of the compound was measured ranges of 200-500 nm. The analyzed spectra were obtained by subtracting the spectrum of pure solvent (water) from that of the solution containing caffeic acid. The experimental method implemented to study the self-association of caffeic acid is similar with method applied by[12], for studying 5-caffeoylquinic acid. The change in the shape of the spectrum, shift of maximum absorbance and isobestic points at three wavelengths indicating the existence of two different species. The self-association of the compound was studied over the concentrations ranges of (1.67-10.00) x10-5 and (2.59-23.90) x10-5 M in acetonitrile and water solutions respectively. The self-association can be detected over a wide range of concentration and need a careful examination of the changes in the apparent molar absorptivity. The absorbance as a function of concentration were measured at 286 and 318 nm wavelengths in acetonitrile and water respectively.On the other hand for studying the complexation of caffeic acid with sodium ions, the aqueous solution of sodium hydroxide (1.89-3.04) x10-3 M and caffeic acid 5.83x10-5 M solution were prepared in water. The electronic absorption spectra of the complex solution recorded at various concentrations of sodium hydroxide solutions. The thermodynamic parameters of caffeic acid self-association in water solution were calculated at temperature of 328 K. For numerical analysis the molar absorptivity and equilibrium constants, dimer model for self-association of caffeic acid and Benesi-Hildebrand approach for the complexation with sodium ions were used. Numerical procedure of fitting the dimer model to experimental data was carried out by non-linear curve fitting based on Levenberg- Marquardt algorithm. The molar absorptivity and equilibrium constants were used as searching parameters in order to achieve the minimum discrepancy between the experimental data and theoretical expression.
3. Results and Discussion
3.1. Concentration Dependent Self-Association of Caffeic Acid
Fig 1 shows the absorption spectra of caffeic acid in acetonitrile which has lack of hydroxyl group. In the concentration ranges of (1.67-10) x10-5 M caffeic acid has three isobestics at the wavelength of 254, 282 and 374 nm respectively. In addition, shift of peak maximum, increase and decrease the intensity spectra at different absorption regions were observed relevant to the concentration of caffeic acid. 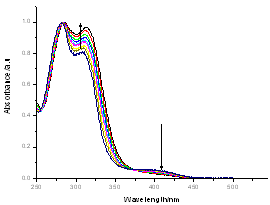 | Figure 1. the electronic absorption spectra of caffeic acid in acetonitrile in the concentration ranges of (1.67-10) x10-5 M |
Absorption spectra of caffeic acid measured in distilled water for two different concentrations at room temperature. The dot shows the absorption spectrum of caffeic acid at concentration of 23.9x10-5 M. In this concentration, the main absorption bands of caffeic acid are double band at 294 and 319 nm and other located at 217 nm. On the other hand the line shows the caffeic spectrum at the concentration of 1.49x10-5 M; in this case the peaks were observed at 287, 312 and 215 nm respectively. Like that in acetonitrile shift of peak maxima, intensity variation at peaks and four isobestic points at (225, 255, 283 and 374 nm) were observed relevant to the concentration. When the concentrations of caffeic acid are greater than 5.31x10-5 M, the peak intensity at the wavelength (~319 nm) greater than the two peak band; however; for concentration less than 5.31x10-5 M, the peak intensity at the wavelength (~215 nm) greater than the two peaks found at higher wavelength. The shift of maximum absorbance, intensity variation and isobestic points, clearly suggests the existence of self-association of caffeic acid due to hydrogen bonding of carboxylic groups. This has also been reported by[13-14], that the dimer of caffeic is due to hydrogen bond of carboxylic groups.The quantitative analysis of caffeic acid self-association was carried out using the concentration dependence of molar absorptivity of the molecule. The values of molar absorptivity of caffeic acid in water and acetonitrile increase and decrease as the concentration increases respectively. The deviation from Beer-Lambert’s law and depends on concentrations, suggests the existence of self-association process. These effects are plotted in fig 3a-b, where the points show the experimental data and the lines are the dimer model fitted to the experimental data.For numerical analysis of the molar absorptivity of monomer, dimer and dimirazation constant the dimer model were derived as follows. The model was derived by considering the following molecular equilibrium in solutions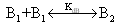 | (1) |
Where, 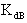 is the equilibrium dimerzation constant,
is the equilibrium dimerzation constant, 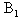 and
and 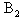 are monomers and dimers of caffeic acid respectively. The over all concentration of the dissolved molecules in solution is given by the mass conservation law,
are monomers and dimers of caffeic acid respectively. The over all concentration of the dissolved molecules in solution is given by the mass conservation law, 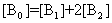 | (2) |
Where, 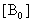 is the total concentration of caffeic acid,
is the total concentration of caffeic acid, 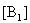 is the monomer concentration and
is the monomer concentration and 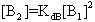 is the concentration of the dimers. The contribution of the monomer and dimer to the molar absorptivity,
is the concentration of the dimers. The contribution of the monomer and dimer to the molar absorptivity, 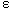 of the solution is commonly considered to be additive,
of the solution is commonly considered to be additive, 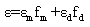 | (3) |
Where, 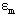 ,
, 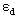 are absorptivity of caffeic acid monomers and dimers respectively.
are absorptivity of caffeic acid monomers and dimers respectively. 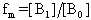 is the equilibrium mole fraction of the molecules in the monomer and
is the equilibrium mole fraction of the molecules in the monomer and 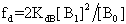 is a mole fraction of the molecules with in the dimer concentration. Concentration
is a mole fraction of the molecules with in the dimer concentration. Concentration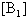 can be determined from the solution of the mass conservation law of equation (2). By substituting the solution of equation (2) in to equation (3) the following dimer model obtained,
can be determined from the solution of the mass conservation law of equation (2). By substituting the solution of equation (2) in to equation (3) the following dimer model obtained, 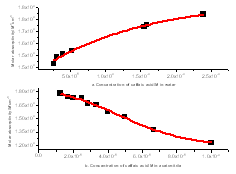 | Fiure 3. a) the molar absorptivity versus concentration of caffeic acid in water at maximum wavelength ( λmax=318 nm) and b) the molar absorptivity versus concentration of caffeic acid in acetonitrile at maximum wavelength ( λmax= 286 nm) |
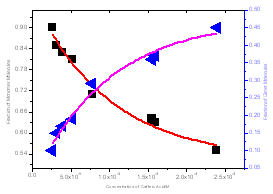 | Figure 4. the mole fraction of monomer and dimer versus total concentration of caffeic acid in water solution |
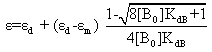 | (4) |
In equation (4) there are three unknown parameters, 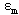 ,
, 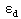 and
and 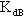 which can be obtained from numerical analysis of experimental concentration dependence of the molar absorptivity of caffeic acid in acetonitrile and water solutions, fig 3 and 4.The values of these three quantities were computed by nonlinear regression based on the Lavenberg-Marquardt algorithm by origin software. The three quantities are serving as a search parameters being adjusted in order to achieve the minimum discrepancy between the experimental data and equation (4).By this method the values o
which can be obtained from numerical analysis of experimental concentration dependence of the molar absorptivity of caffeic acid in acetonitrile and water solutions, fig 3 and 4.The values of these three quantities were computed by nonlinear regression based on the Lavenberg-Marquardt algorithm by origin software. The three quantities are serving as a search parameters being adjusted in order to achieve the minimum discrepancy between the experimental data and equation (4).By this method the values o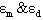 ,
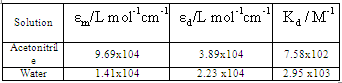
,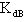 were calculated for caffeic acid in acetonitrile and water solutions and these values are shown in table 1. The obtained values are quite reasonable and comparable with the results obtained by other workers in the UV region of the spectrum for other molecules. The values of
were calculated for caffeic acid in acetonitrile and water solutions and these values are shown in table 1. The obtained values are quite reasonable and comparable with the results obtained by other workers in the UV region of the spectrum for other molecules. The values of 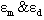 determined for lauric acid in liquid of CCl4 using FTIR were 2.8x104 and 8.66x103 L mol-1 cm-1 respectively[15]. Furthermore, the self-association constant and monomer molar absorptivity determined for studied in aqueous solution at high pH value would be 1x104 M-1 and 1.5x104 M-1 cm-1 respectively[16]. Moreover, the calculated dimerzation constant of caffeic in water in this research is quite similar with the dimerzation constant calculated for 5-caffeoylquinic acid and reported by[12]
determined for lauric acid in liquid of CCl4 using FTIR were 2.8x104 and 8.66x103 L mol-1 cm-1 respectively[15]. Furthermore, the self-association constant and monomer molar absorptivity determined for studied in aqueous solution at high pH value would be 1x104 M-1 and 1.5x104 M-1 cm-1 respectively[16]. Moreover, the calculated dimerzation constant of caffeic in water in this research is quite similar with the dimerzation constant calculated for 5-caffeoylquinic acid and reported by[12]Table 1. the molar absoptivity of monomer, dimer and dimerzation constant of caffeic acid in acetonitrile and water solutions
 |
| |
|
The fraction of monomer and dimer molecules versus total caffeic acid concentration were also determined in water solution and shown in fig 4. The formations of dimer molecules are favored by high concentration, in which the fraction of monomer and dimer molecules are decrease and increase respectively.
3.2. The Complexation of Sodium ions with Caffeic Acid
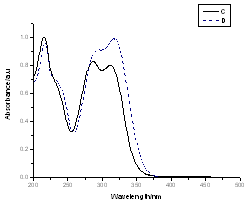 | Figure 2. the electronic absorption spectra of caffeic acid in water for two different concentrations. The dot shows the spectrum of caffeic acid at C= 23.9x10-5 M and line the spectrum at C=1.49x10-5 M |
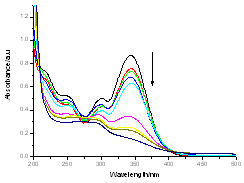 | Figure 5. The UV-Visible absorption spectra for titration of caffeic acid (5.83x10-5 M) with aqueous of sodium hydroxide (7.59x10-3M) |
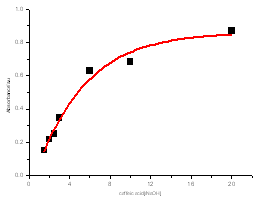 | Figure 6. Absorbance versus mole ratio ([caffeic acid]/[Sodium hydroxide]) at 343 nm |
The electronic absorption spectrum of free caffeic acid in water solution shown in figure 2 has mainly characterized by double absorption band at 318 and 294 nm and other band located at 216 nm. The addition of anhydrous of sodium hydroxide to caffeic acid solution in water result in spectral modification and apparition of a new band at higher wavelength (343 nm). In addition, a decrease in absorbance is obsorbed upon addition of increasing quantities of sodium ions to caffeic acid solution as shown in fig 5. These changes could be attributed to the complexation between the ligand (caffeic acid) and sodium ions. The mole ratio method was used to determine the stoichiometry of complexed forms of caffeic acid with sodium ions. The absorbance versus molar ratio plot at the wavelength of 343 nm fig 6 the stoichiometry Na ion:Caffeic acid=1:3. This result is similar with the report by[5] for the complexation of caffeic acid with aluminuim ions.The complexation of Na+ with caffeic acid coordinating at carboxylic and catechol sites by releasing the H+ from oxygen. Many literatures are also described the strong bind of metal ions with oxygen-donar ligands and the chealting power of this compound at catechol and carboxylic groups with Al (III) and Pb (II) were also studied by[4-5] previously. Fig 5 shows peak absorbance vs various concentration of sodium hydroxide in caffeic acid solutions or ([NaOH]:[Caffeic acid] for the ratio of 07-87) at peak 343 nm. Furthermore, the isobestic points in the absorption spectra, which are also the indicative of the complex formation between sodium ions and caffeic acid The quantitative analysis of the complexation of sodium ions with caffeic acid was accomplished using Benesi-Hildebrand approaches[17], under the condition of[B0] >>[A0]. A caffeic acid solution of ([CA] =[A0] =5.83x10-5 M=constant) and different concentrations of sodium hydroxide ([NaOH] =[B0] = (1.89-3.04) x10-3 M were used to calculate the equilibrium constant and molar extinction coefficient of the complex formation. The equilibrium constant for the complex formation K, derived as follows,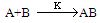 | (5) |
The equilibrium constant for the complex formation, K can be defined as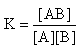 | (6) |
Where,[A],[B], and[AB], are the equilibrium concentration of caffeic acid, sodium hydroxide and association of caffeic acid with sodium respectively. If the initial concentration of caffeic acid and sodium hydroxide designated as[A0] =[A] +[AB] and[B0] =[B] +[AB], substituting these in to Eq (6) it gives,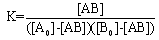 | (7) |
For[B]>>[A], the[B0]-[AB] approximately becomes[B0], so Eq (7) can be written as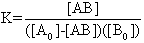 | (8) |
After re-arranging Eq (8) it gives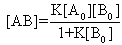 | (9) |
The absorbance (A) for concentration[AB] according to Beer's law is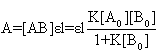 | (10) |
Eq (10) can be re-arranged as follow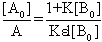 | (11) |
When the path length l=1cm, Eq (11) can be written in the form of Benesi-Hildebrand equation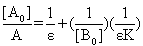 | (12) |
The plot of 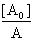 vs.
vs. 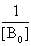 gives a straight line (R=0.99) with y-intercept
gives a straight line (R=0.99) with y-intercept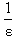 and slope
and slope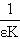 . By this method the equilibrium constant for the complex formation and molar extinction coefficient calculated at peak position were K=6.86x103 M-1 and 1.40x104 M-1 cm-1 respectively. The equilibrium constant for the complex formation with sodium is with in the range of the dimerzation constants of caffeic acid.
. By this method the equilibrium constant for the complex formation and molar extinction coefficient calculated at peak position were K=6.86x103 M-1 and 1.40x104 M-1 cm-1 respectively. The equilibrium constant for the complex formation with sodium is with in the range of the dimerzation constants of caffeic acid.
3.3. Thermodynamic Properties of the Self-association of Caffeic Acid
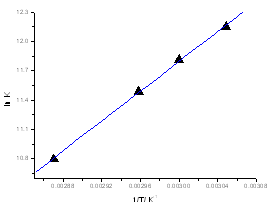 | Figure 7. the Van’t Hoff plots for self-association of caffeic acid at concentration (C=5.83x10-5 M) |
Heating the aqueous solution of caffeic acid shows that the absorption spectra of the molecules are strongly dependent on the temperature in the range of (328-348 K). As temperature increases, the absorption intensity increases which indicate a dissociation of the molecular associated forms in the solutions. Fig 7 shows the graph of ln KdB versus f(1/T) ,of caffeic acid, which is linear. The magnitude of the enthalpy was estimated from the slope of the approximating line according to 's equation: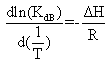 | (13) |
Where, 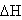 is the molar enthalpy change, R= 8.31 J mol-1 K-1 , the universal gas constant and temperature in Kelvin. The entropy was derived from Gibb's free energy and enthalpy. The Gibb's free energy can be expressed as
is the molar enthalpy change, R= 8.31 J mol-1 K-1 , the universal gas constant and temperature in Kelvin. The entropy was derived from Gibb's free energy and enthalpy. The Gibb's free energy can be expressed as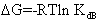 | (14) |
The entropy becomes 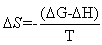 | (15) |
The calculated values of Gibb’s free energy, enthalpy and entropy of caffeic acid self-associations are -34.06, -63.20  and -88.84
and -88.84  respectively. These values are in good agreement with the results reported by[9] using fluormertic and quantum chemical methods for 1:1 stoichimetry molecular association between caffeic acid and malvidin3-O-glucoside. From obtained results the self-association of caffeic acid are exothermic which are characterized by relatively large negative of change in enthalpy
respectively. These values are in good agreement with the results reported by[9] using fluormertic and quantum chemical methods for 1:1 stoichimetry molecular association between caffeic acid and malvidin3-O-glucoside. From obtained results the self-association of caffeic acid are exothermic which are characterized by relatively large negative of change in enthalpy
4. Conclusions
The concentration dependent self-association of caffeic and its hetero-association with sodium hydroxide were reported in water solution by UV-Vis spectroscopy at room temperature. A shift of maximum absorbance and isobestic points relevant to the concentration of caffeic acid indicates the self -association of molecules due to carboxylic or catechol groups. Similarly the appearance of new band at higher wavelength, decrease in relative absorbance and the existence of two isobestic points in the mixed solution of caffeic acid and sodium hydroxide show the hetero-association of the molecules. Understanding the mechanism of self-association of caffeic acid is useful in order to design the advanced and controllable carriers of drugs and food components. On the other hand the results obtained from complexation of the compound with sodium ions are great applications in extraction alkali metals ions selectively from natural environment.
References
| [1] | RW Jiang, KM Lau, P M Hona , T CW Mak, K S Woo, K P Fung, Current Medicinal chemistry 12 237-246 (2005). |
| [2] | J Iglesias, M Pazos, M L Andersen. L H Skibsted, I Medina, Agriculture and Food Chemistry, 57, 675-681(2009). |
| [3] | C Giacomellic, K Ckless, D Galato, F S Miranda, A Spinelli, J.Braz.Chem.Soci. 3 332-338 (2002). |
| [4] | J P Cornard, C Lapouge, J.Phys.Chem 108 4470-4478 (2004). |
| [5] | J P Cornard, A Caudron., J C Merlin, Polyhedron 25 2215-2222 (2006). |
| [6] | A M Khvan, E L Kristallovich, K A Abduazimov Chemistry of Natural Compounds 37 72-76 (2001). |
| [7] | M J Hynes, M Ocoinceanainn, Journal of Inorganic Biochemistry 98 1457-1464(2004). |
| [8] | P Gornas, G Neunert, K Bacyynski, K Polewski, Food Chemistry 114 190 -196(2009). |
| [9] | S K Mate, E Stampel, L Kollar, M S P Nikfardjam, Food Research International 41 693-696 (2008). |
| [10] | J C Dearden, Canadian Journal of Chemistry, 41 2683-2691(1963). |
| [11] | N Marme, G Habl, J P Knemeyer, Chemical Physics Letter 408 221-225(2005). |
| [12] | A Belay, International Journal of Physical Science 5 459-464 (2010). |
| [13] | M Ge, H Zhao, W Wang, Z Zhang, X Yu, W Li, J Bio Phys 32 403-412 (2006). |
| [14] | A. Belay, 55th International Conferences on Analytical Science and Spectroscopy, August, 9-12, 2009 Kingston Ontario, Canada. |
| [15] | J Lu , B Han, H Yan, Phys.Chem.Chem.Phys., 1, 449-453 (1999). |
| [16] | P Peral, E Gallego, Biophysical Chemistry, 85 79-92 (2000). H A Benesi , J H Hildebrand, J.Am.Chem.Soc. 71 2703-2707(1949). |


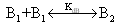
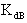 is the equilibrium dimerzation constant,
is the equilibrium dimerzation constant, 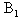 and
and 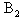 are monomers and dimers of caffeic acid respectively. The over all concentration of the dissolved molecules in solution is given by the mass conservation law,
are monomers and dimers of caffeic acid respectively. The over all concentration of the dissolved molecules in solution is given by the mass conservation law, 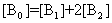
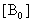 is the total concentration of caffeic acid,
is the total concentration of caffeic acid, 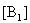 is the monomer concentration and
is the monomer concentration and 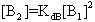 is the concentration of the dimers. The contribution of the monomer and dimer to the molar absorptivity,
is the concentration of the dimers. The contribution of the monomer and dimer to the molar absorptivity, 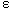 of the solution is commonly considered to be additive,
of the solution is commonly considered to be additive, 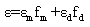
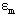 ,
, 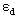 are absorptivity of caffeic acid monomers and dimers respectively.
are absorptivity of caffeic acid monomers and dimers respectively. 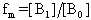 is the equilibrium mole fraction of the molecules in the monomer and
is the equilibrium mole fraction of the molecules in the monomer and 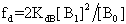 is a mole fraction of the molecules with in the dimer concentration. Concentration
is a mole fraction of the molecules with in the dimer concentration. Concentration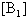 can be determined from the solution of the mass conservation law of equation (2). By substituting the solution of equation (2) in to equation (3) the following dimer model obtained,
can be determined from the solution of the mass conservation law of equation (2). By substituting the solution of equation (2) in to equation (3) the following dimer model obtained, 
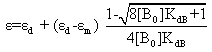
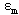 ,
, 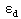 and
and 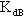 which can be obtained from numerical analysis of experimental concentration dependence of the molar absorptivity of caffeic acid in acetonitrile and water solutions, fig 3 and 4.The values of these three quantities were computed by nonlinear regression based on the Lavenberg-Marquardt algorithm by origin software. The three quantities are serving as a search parameters being adjusted in order to achieve the minimum discrepancy between the experimental data and equation (4).By this method the values o
which can be obtained from numerical analysis of experimental concentration dependence of the molar absorptivity of caffeic acid in acetonitrile and water solutions, fig 3 and 4.The values of these three quantities were computed by nonlinear regression based on the Lavenberg-Marquardt algorithm by origin software. The three quantities are serving as a search parameters being adjusted in order to achieve the minimum discrepancy between the experimental data and equation (4).By this method the values o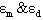 ,
,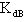 were calculated for caffeic acid in acetonitrile and water solutions and these values are shown in table 1. The obtained values are quite reasonable and comparable with the results obtained by other workers in the UV region of the spectrum for other molecules. The values of
were calculated for caffeic acid in acetonitrile and water solutions and these values are shown in table 1. The obtained values are quite reasonable and comparable with the results obtained by other workers in the UV region of the spectrum for other molecules. The values of 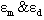 determined for lauric acid in liquid of CCl4 using FTIR were 2.8x104 and 8.66x103 L mol-1 cm-1 respectively[15]. Furthermore, the self-association constant and monomer molar absorptivity determined for studied in aqueous solution at high pH value would be 1x104 M-1 and 1.5x104 M-1 cm-1 respectively[16]. Moreover, the calculated dimerzation constant of caffeic in water in this research is quite similar with the dimerzation constant calculated for 5-caffeoylquinic acid and reported by[12]
determined for lauric acid in liquid of CCl4 using FTIR were 2.8x104 and 8.66x103 L mol-1 cm-1 respectively[15]. Furthermore, the self-association constant and monomer molar absorptivity determined for studied in aqueous solution at high pH value would be 1x104 M-1 and 1.5x104 M-1 cm-1 respectively[16]. Moreover, the calculated dimerzation constant of caffeic in water in this research is quite similar with the dimerzation constant calculated for 5-caffeoylquinic acid and reported by[12]

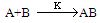
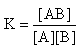
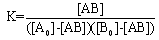
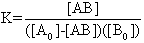
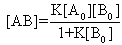
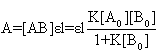
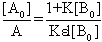
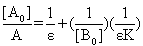
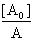 vs.
vs. 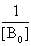 gives a straight line (R=0.99) with y-intercept
gives a straight line (R=0.99) with y-intercept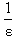 and slope
and slope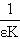 . By this method the equilibrium constant for the complex formation and molar extinction coefficient calculated at peak position were K=6.86x103 M-1 and 1.40x104 M-1 cm-1 respectively. The equilibrium constant for the complex formation with sodium is with in the range of the dimerzation constants of caffeic acid.
. By this method the equilibrium constant for the complex formation and molar extinction coefficient calculated at peak position were K=6.86x103 M-1 and 1.40x104 M-1 cm-1 respectively. The equilibrium constant for the complex formation with sodium is with in the range of the dimerzation constants of caffeic acid.
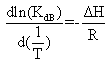
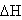 is the molar enthalpy change, R= 8.31 J mol-1 K-1 , the universal gas constant and temperature in Kelvin. The entropy was derived from Gibb's free energy and enthalpy. The Gibb's free energy can be expressed as
is the molar enthalpy change, R= 8.31 J mol-1 K-1 , the universal gas constant and temperature in Kelvin. The entropy was derived from Gibb's free energy and enthalpy. The Gibb's free energy can be expressed as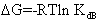
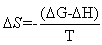
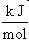 and -88.84
and -88.84 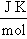 respectively. These values are in good agreement with the results reported by[9] using fluormertic and quantum chemical methods for 1:1 stoichimetry molecular association between caffeic acid and malvidin3-O-glucoside. From obtained results the self-association of caffeic acid are exothermic which are characterized by relatively large negative of change in enthalpy
respectively. These values are in good agreement with the results reported by[9] using fluormertic and quantum chemical methods for 1:1 stoichimetry molecular association between caffeic acid and malvidin3-O-glucoside. From obtained results the self-association of caffeic acid are exothermic which are characterized by relatively large negative of change in enthalpy Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML

