-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Biophysics
2012; 2(1): 1-6
doi: 10.5923/j.biophysics.20120201.01
Equation Chapter 1 Section 1A Thermodynamic Perspective on the Interaction of Radio Frequency Radiation with Living Tissue
Michael Peleg
Rafael Ltd, Haifa, Israel and Technion-Israel Institute of Technology, Haifa, Israel
Correspondence to: Michael Peleg , Rafael Ltd, Haifa, Israel and Technion-Israel Institute of Technology, Haifa, Israel.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The existence of biological effects of radio frequency (RF) radiation on living tissue is well established, including also effects which are non-thermal, that is not caused by plain uniform warming. Still the exact mechanisms of interaction between the RF radiation and the living tissue are mostly unknown. In this work a thermodynamic perspective relevant to some aspects of those yet unknown mechanisms is presented. This perspective reveals that living tissue under RF radiation should not be assumed to be in thermal equilibrium since it is governed by two temperatures: the ambient temperature of its surroundings and a vastly higher temperature TR which is assigned by certain criteria to the RF radiation. The criteria presented here to determine the radiation temperature TR are not unique and other approaches may lead to different temperature values, however TR as presented here has an interesting physical significance. The possible relevance of this approach to the interaction mechanisms is presented; specifically some molecules in the living tissue may acquire much more energy than the one associated with the ambient temperature and biological effects may occur.
Keywords: radio frequency, thermodynamics, statistical physics, biology, electromagnetic, cancer, nonionizing radiation, black body radiation
Article Outline
1. Introduction
- The existence of biological effects of Radio Frequency (RF) radiation on living tissue is well established by works such as[1-3] and many others which identified specific biological effects on cells and organs. Many of those effects are non-thermal, that is they are not caused by plain and uniform warming. Carcinogenic influence was indicated by many researches such as[4,5] and [6] and RF radiation is classified as a possible carcinogen for humans by the International Agency for Research on Cancer (IARC). Still, the exact interaction mechanisms between the RF radiation and the living tissue are mostly unknown as pointed out recently also by IARC although many possibilities have been discussed, e.g. [7]. Some works such as[1] identified biological effects of RF radiation on separated living cells floating in a homogenous solution without any large antenna-like structures. Thus one should look also for direct interactions between RF radiation and cellular or biochemical processes. The interaction mechanisms may be very complex as is the living tissue itself, thus state of the art physics, chemistry and biology will be required to identify them. Indeed, initial interesting research attempting this has been reported, see for example[8] with its many references and[9].In this paper I present a new thermodynamic perspective which may illuminate an interesting aspect of some of the interaction mechanisms. It shows that a living tissue under RF radiation should not be assumed to be in thermal equilibrium since it is governed by two temperatures: The ambient temperature of its surroundings denoted TA and a vastly higher temperature denoted TR which is assigned by certain criteria to the RF radiation. The criteria presented here to determine TR are not unique and other approaches may lead to different temperatures, however TR as presented here has an important physical significance which will be explained. Hypotheses about possible interaction mechanisms based on this perspective are presented. RF comprises the electromagnetic spectrum of frequencies from about 0.5 MHz to about 200 GHz. In this paper I shall use a RF of 109 Hz or 1 GHz as a representative value for cellular transmission frequencies which typically occupy bands centred on 0.9 GHz and on 1.8 GHz.This paper examines interaction of systems with different temperatures thus involving non-equilibrium thermodynamics. This is treated here using the approximation of Local Thermodynamic Equilibrium (LTE). LTE is a state in which a system of particles achieves approximately the same properties as a system in a full (global) thermodynamic equilibrium despite an external influence such as slow flow of energy which may change its temperature. LTE occurs when the interaction between the particles in the system is fast enough to redistribute the incoming influence and achieve statistical distributions similar to those associated with thermodynamic equilibrium. LTE is used widely to accommodate the concept of meaningful and non-uniform temperature, see[10,11] for examples involving radiation.
2. The Radiation Temperature
- Let us consider man-made RF radiation at some intensity d in watts/m2 radiated by some transmitter, for example the Israeli safety limit of 50 microwatts/cm2 at the frequency f=1GHz. Assigning a temperature value to this intensity is not straightforward because radiation is not a classical closed system in a thermodynamic equilibrium. We shall assign the temperature by similarity to the classical black body radiation using the two following ad-hoc rules:Rule 1: The radiation temperature TR will be defined as the temperature at which the black body radiation achieves the same energy density in J/m3 as the man-made radiation in question where J denotes Joule and m is meter.Rule 2: The energies of the man-made and of the black body radiations will be summed over the 0 to f Hz frequency band where f is the maximal frequency used by the transmitter; we shall use 1 GHz in our examples. Thus the energy of the black body radiation outside this band will be discarded. This rule has the intuitive appeal of comparing the same frequencies of both the types of radiation and its exact significance will be demonstrated in the thought experiment section below.Deriving TR by following those rules is straightforward. The energy per unit volume per bandwidth in J/m3/Hz of black body radiation is, by the Rayleigh–Jeans law e.g. [12, chapter 16]:
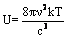 | (1) |
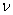 is the frequency in Hz, k is the Boltzmann constant in J/OK, c is the speed of light in m/sec and T is the absolute temperature in OK (Degrees Kelvin). See Figure 1.
is the frequency in Hz, k is the Boltzmann constant in J/OK, c is the speed of light in m/sec and T is the absolute temperature in OK (Degrees Kelvin). See Figure 1.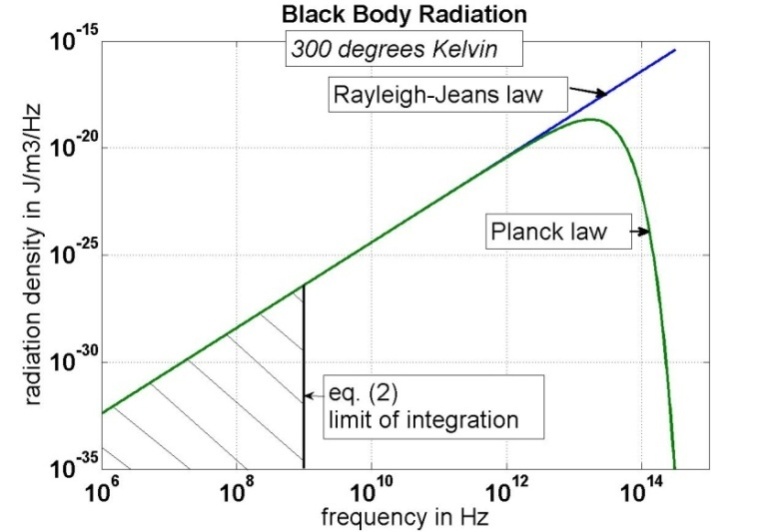 | Figure 1. Black body radiation spectra at 300 OK. The shaded area is integrated over in eq. (2) |
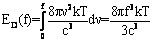 | (2) |
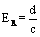 | (3) |
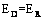 and using equations (2) and (3):
and using equations (2) and (3):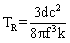 | (4) |
3. A Thought Experiment
3.1 Thermally insulating enclosure
- We construct a large enclosure and place it on the Earth's surface near a cellular base-station at a distance where the radiation density is d=50 microwatt/cm2 as in figure 2.
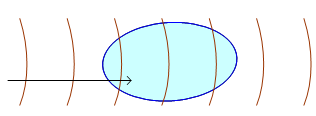 | Figure 2. Large enclosure in an RF radiation field |
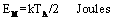 | (5) |
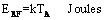 | (6) |
3.2 Partially Heat Conducting Enclosure
- Next let us change the wall material to one having some thermal conductivity. Then the system comprising the non-RF modes in the interior will be at an intermediate temperature TI somewhere in the range between TA and TR. The temperature will depend on the coupling between the radiation and the enclosure interior which will determine the energy transfer rate from the incoming radiation to the interior non-RF modes and on the thermal conductivity of the enclosure walls which will determine the thermal energy transfer rate from the interior. Clearly the enclosure interior isn't now in a thermal equilibrium since the RF modes are at higher energies than the non-RF modes. The coupling of the RF modes to the non-RF modes typical to the human body is very low relatively to the coupling between the non-RF modes and between those and the surroundings; otherwise the non-RF modes would reach temperatures of the order of TR which would be catastrophic. Thus the strong coupling between the non-RF modes facilitates redistribution of the slow inflow of energy from the RF modes and the non- equilibrium system can be modelled as a union of three sub-systems with heat transfer between them, each being in LTE. The first subsystem comprises the RF modes in the enclosure interior, the second the non-RF modes in the enclosure and the third the enclosure exterior at temperature TA, see figure 3.The thought experiment and the calculations could have been carried out by exactly the same method over a narrower frequency band identical to that used by the actual base station by integrating eq. (2) from f1 to f2 defining the limits of the frequency band. However then the transparency of the wall enclosure would have to be limited to the same frequency band, which is not an expected attribute of a living tissue.
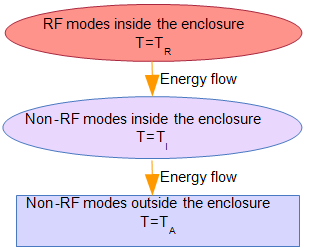 | Figure 3. The thought experiment with thermally conducting enclosure wall - the three subsystems in Local Thermodynamic Equilibrium (LTE) |
4. Two Models of a Living Tissue
- Let us examine the relevance of the thought experiment to a living tissue exposed to RF radiation in a realistic setting with no enclosure. We shall focus on the distribution of energy between the modes as discussed above while using the homogenous and non-homogenous models presented next.
4.1. The Homogenous Model
- In this model the non-RF modes in the living tissue can exchange energy freely among themselves and their coupling to the RF modes is existent but weak. Then the energy between the non-RF modes is distributed evenly. This model is very similar to our thought experiment with thermally conducting enclosure wall depicted in figure 3 where now the enclosure interior corresponds to the living tissue. The system comprising the non-RF modes will be at LTE at some temperature TI and all the non-RF modes will acquire typically the same average thermal energy of kTI/2. With the weak RF coupling and high thermal conductivity typical to the human body, the temperature TI will be only slightly above the usual 36.5℃ (degrees Celsius) at radiation intensities below the thermal limits set by the International Commission on Non-Ionizing Radiation Protection (ICNIRP). This is the model fitting the ICNIRP assumptions.
4.2. The Non-Homogenous Model
- Now suppose that some non-RF mode, due to the structure of some special molecule, is more strongly coupled to the RF radiation field then the other modes and is more loosely thermally coupled to the other non-RF modes. The energy per RF mode will be still kTR. The energy transfer from the RF modes to this special non-RF mode will be faster and the rate at which this energy is dissipated to the other modes will be slower than the average. Thus this mode will acquire more energy from the radiation field than the average kTI/2 energy set by the temperature TI of its surroundings. To apply the concept of temperature let us examine small regions of such special modes, see figure 4 with 3 such regions, each at LTE at temperature Δi + TI, i=1,2,3. Let us assume that the energy transfer R in watt/sec from any region at temperature T1 to another region at temperature T2 in our model are linear functions of temperature difference such that
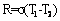 where σ denotes the region-specific thermal conductance and denote σRi and σi the thermal conductance from the RF modes to the special region number i and from this region to the surrounding tissue respectively. Then an easy derivation yields at the steady state
where σ denotes the region-specific thermal conductance and denote σRi and σi the thermal conductance from the RF modes to the special region number i and from this region to the surrounding tissue respectively. Then an easy derivation yields at the steady state 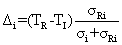 | (7) |
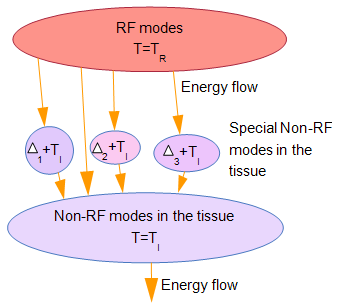 | Figure 4. Details of the non-homogenous model |
5. Examining Relevance to Known Biological Effects
- The minimal energy required to change a living tissue is hard to estimate. One clue is the fact that the human body feels well at 36.5℃ and ill at 40℃, thus a ΔT=3.5℃ temperature difference has a significant influence on some tissues in the human body. This corresponds to incrementing the average energy per mode by kΔT/2, this is 1.47x10-4 eV (electron-Volt), much less then the thermal energy per thermodynamic degree of freedom kT/2. See an interesting discussion of known sub-kT biological effects in[15].It is conceivable that in the presence of RF radiation some special modes will acquire more energy than dictated by the average temperature TI as described above and a biological change will occur. Such a process will be impeded by the weak coupling of the RF field to the non-RF modes and by the strong thermal coupling between the non-RF modes, and, on the other hand, it will be driven by the huge temperature TR which is vastly larger than the small temperature difference ΔT capable of inducing a biological change, see eq.(7). The interaction mechanism may operate on a few molecules out of many taking them out of the thermal equilibrium without noticeable increase in the average tissue temperature.Such processes are not identified yet at the detail of the interaction between the RF field and a particular molecule; however, using[1] as a prominent example, it was established that a biological process in human cells starting with the activation of NADH oxidase and identified exactly at the molecular level was initiated by a weak RF field, thus there is some mechanism of interaction. Also the review paper[3] presents many experimental results on DNA damage in human cells caused by RF radiation, states that the exact interaction mechanism is yet unknown and describes possible mechanisms involving free radicals, mitochondria, iron atoms catalysing the Fenton reaction which produces the free radicals and notes that brain cells may be sensitive to RF damage due to high free iron levels and high metabolism. As stated in the introduction, the existence of non-thermal effects of RF fields is firmly established, the only open question are the mechanisms of interaction themselves. The thermodynamic perspective presented here may be relevant to some of the mechanisms of interaction; other mechanisms to which this perspective is less relevant are possible such as the hypotheses on interaction with groups of water molecules examined for example by[9].The absorption of RF energy in the living tissue is not uniform but varies widely over parts of each single cell as shown by[16]; the measured Specific Absorption Rate (SAR) reflects the average, not the actual absorption of RF energy in various parts of each cell. Thus the interaction of the RF modes discussed above with the living tissue is already known to be non-uniform. There are many sources of non-uniformity and non-equilibrium in the living tissue apart of the RF radiation discussed here. Some of those fulfil essential roles in the living process. The known biological non-uniformities may cause non-uniform interaction with the RF fields. Mitochondria which are utilizing chemical energy for life processes in every human cell are just one example of non-uniformity listed in[3] as a site of a possible interaction mechanism.
6. Conclusions
- A new thermodynamic perspective on possible interaction mechanisms between RF radiation and the living tissue has been presented. From this perspective the RF radiation can be considered as extremely hot and as weakly coupled to the molecules of the living tissue. The energy acquired by a particular molecule depends on how fast the energy flows from the electromagnetic field to the molecule and how fast it is then dissipated to the surroundings. Significant interaction between RF radiation and the living tissue at sub- thermal radiation levels is compatible with this perspective if the interaction is not uniform and some molecules or modes acquire significantly more energy than the average.This paper did not discover a new mechanism of interaction; rather it showed possible attributes of such a mechanism and demonstrated that the existence of such an interaction mechanism is well compatible with known physical principles and with known biology. It is also possible that an actual mechanism will turn out to be very different.
ACKNOWLEGEMENTS
- I wish to thank Osmo Hänninen and Zamir Shalita for valuable advice on biology and Iris Atzmon for insightful remarks. I thank the anonymous reviewer for important comments and suggestions which improved the quality of the paper.
APPENDIX
- The Energy of the Rf Modes in the EnclosureThe transparency of the enclosure wall, that is the ratio between the energy passing thru the wall to the energy incident on the wall, is similar in both the incoming and the outgoing directions. This is guaranteed under very mild conditions by the well-known reciprocity of RF propagation. Also, after sufficient time, the total flow of the RF energy into the enclosure must be equal to the flow escaping from the enclosure to reach a steady state. Thus the radiation density inside the enclosure is similar to that outside it for any transparency of the enclosure wall.When the transparency of the wall is low, the enclosure interior is nearly isolated from its exterior and most of the RF energy inside the enclosure is stored in the RF modes which are shaped by the enclosure geometry. The classical black body radiation theory exhibits one to one relationships between the temperature, between the RF energy density in J/m3 and between the average energy per RF mode, see eq.(1) and (6). Then, since the interior and the exterior radiation density is related to TR by eq. (1) where T=TR, the average energy per RF mode is kTR by eq.(6).With higher transparency the energy density inside the enclosure cannot change much as explained in the beginning of this appendix, only the standing wave patterns are modified and more coupled to the outside radiation. This will modify the details of the coupling of the RF modes to the other modes but will not change drastically the coupling magnitude, the energy of the non-RF modes and the interior temperature.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML