| [1] | Noireaux V., Libchaber A. A. Vesicle bioreactor as a step toward an artificial cell assembly, PNAS, Vol. 101, pp. 17669-17674 (2004). |
| [2] | Noireaux V., Bar-Ziv R., Godefroy J., Salman H., Libchaber A. Toward an artificial cell based on gene expression in vesicles. Phys. Biol., Vol. 2, No 3, pp. 1-8 (2005). |
| [3] | Murtas G., Construction of a Semi-Synthetic Minimal Cell: A Model for Early Living Cells. Origins of Life and Evolution of Biospheres, Vol. 37, No 4-5, pp. 419-422 (2007). |
| [4] | Lartigue C., Glass J. I., et al. Genome Transplantation in Bacteria: Changing One Species to another. Science, Vol. 317, pp. 632-638 (2007). |
| [5] | Gibson D.G., Glass J.I., et al. Creation of a Bacterial Cell Controlled by a Chemically Synthesized Genome. Science, Vol. 329, pp. 52-56 (2010). |
| [6] | Rasmussen S., Chen L., Deamer D., Krakauer D., Packard N., Stadler P., Bedau M. Transitions from nonliving to living matter. Science, Vol. 303, pp. 963-965 (2004). |
| [7] | Müller A., Roy S. Multifunctional Metal Oxide Based Nanoobjects: Spherical Porous Capsules/Artificial Cells and Wheel-Shaped Species with Unprecedented Materials Properties. J. Mater. Chem., Vol. 15, p. 4673-4677 (2005). |
| [8] | Müller A., Toma L., et al. Reactions inside a porous nanocapsule/artificial cell: encapsulates’ structuring directed by internal surface deprotonations. Chem. Commun., Vol. 32, pp. 3396–3398 (2006). |
| [9] | Cooper G.J.T., Kitson P.J., Winter R.S., Zagnoni M., Long D-L., Cronin L. Modular Redox-Active Inorganic Chemical Cells: iCHELLs. Angew. Chem. Int. Ed., Vol. 50, pp. 10373-10376 (2011). |
| [10] | Mansy S.S., Szostak J.W. Reconstructing the Emergence of Cellular Life through the Synthesis of Model Protocells. Cold Spring Harb. Symp. Quant. Biol., Vol. 74, pp. 47-54 (2009). |
| [11] | Mansy S.S., Schrum J.P., Krishnamurthy M., Tobé S., Treco D.A., Szostak J.W. Template-directed synthesis of a genetic polymer in a model protocell. Nature, 2008, Vol. 454, pp. 122-125. |
| [12] | Deamer D. On the origin of systems. Systems biology, synthetic biology and the origin of life. EMBO Rep., No. 10(S1), pp. S1-S4 (2010) |
| [13] | Turing A. M. The Chemical Basis of Morphogenesis. Phil. Trans. R. Soc. B, Vol. 237, No 641, pp. 37-72 (1952). |
| [14] | Haddad W.M., Chellaboina V.S., Hui Q. Nonnegative and Compartmental Dynamical Systems, 624 p., Princeton University Press, 2010. |
| [15] | Haddad W.M., Nersesov S.G. Stability and Control of Large-Scale Dynamical Systems: A Vector Dissipative Systems Approach, 392p., Princeton University Press, 2011. |
| [16] | Smale S., Hirsch M.W., Devaney R.L. Differential Equations, Dynamical Systems, and an Introduction to Chaos, Second Edition, 425 p., Academic Press, 2003. |
| [17] | Strogatz S.H. Nonlinear Dynamics And Chaos: With Applications To Physics, Biology, Chemistry, And Engineering, 512 p., Westview Press, 2001. |
| [18] | Wiggins S. Introduction to Applied Nonlinear Dynamical Systems and Chaos, 808 p., Springer, 2010. |
| [19] | Feudel U., Kuznetsov S., Pikovsky A. Strange Nonchaotic Attractors: Dynamics Between Order And Chaos in Quasiperiodically Forced Systems, 228 p., World Scientific Pub Co Inc, 2006. |
| [20] | Tel T.., Lai Y.C. Transient Chaos: Complex Dynamics on Finite Time Scales, 512 p., Springer, 2011. |
| [21] | Cooper G.J.T., Kitson P.J., Winter R., Zagnoni M., Long D.-L., Cronin L. Modular Redox-Active Inorganic Chemical Cells: iCHELLs. Angew. Chem. Int. Ed., Vol. 50, Issue 44, pp. 10373–10376 (2011). |
| [22] | Toyota T., Maru N., Hanczyc M.M., Ikegami T., Sugawara T. Self-Propelled Oil Droplets Consuming “Fuel” Surfactant. J. Am. Chem. Soc., 2009, 131 (14), pp. 5012–5013. |
| [23] | Kaushal M., Singh A., Singh B. Adaptive Thresholding for Edge Detection in Gray Scale Images. International Journal of Engineering Science and Technology, Vol. 2(6), pp. 2077-2082 (2010). |
| [24] | Giant Vesicles: Perspectives in Supramolecular Chemistry (Ed. by P.L. Luisi, P. Walde), 426 p., Wiley-Interscience, 2000. |
| [25] | Cell Growth: Control of Cell Size (Ed. by M.N. Hall, R. Martin, G. Thomas), 652 p., Cold Spring Harbor Laboratory Press, 2004. |
| [26] | Mullins C. The Biogenesis of Cellular Organelles, 192 p., Springer, 2010. |
| [27] | Plant Cytoskeleton in Cell Differentiation and Development (Ed. by P. Hussey), 325 p., Blackwell, 2004. |
| [28] | Preston T.M., King C.A., Hyams J.S. Cytoskeleton and Cell Motility, 202 p., Chapman & Hall, 1990. |
| [29] | The Cytoskeleton of Flagellate and Ciliate Protists (Ed. by M. Melkonian, R.A. Andersen, E. Schnepf), 174 p., Springer, 2001. |
| [30] | Kendall K., Kendall M., Rehfeldt F. Adhesion of Cells, Viruses and Nanoparticles, 297 p., Springer, 2010. |
| [31] | Pozrikidis C. Modeling and Simulation of Capsules and Biological Cells, 344 p., Chapman and Hall, 2003. |
| [32] | Pozrikidis C. Computational Hydrodynamics of Capsules and Biological Cells, 327 p., CRC Press, 2010. |
| [33] | Harrison L.G. Kinetic Theory of Living Pattern, 376 p., Cambridge University Press, 2005. |
| [34] | Muramatsu T. Cell Surface and Differentiation,172 p., Springer, 1990. |
| [35] | Interfacial Phenomena in Biological Systems (Ed. by M. Bender), 448 p., CRC Press, 1991 |
| [36] | Fung Y.C. Biomechanics: Motion, Flow, Stress, and Growth, 607 p., Springer, 1990. |
| [37] | Trinkaus J.P. Cells into Organs: The Forces That Shape the Embryo, 560 p., Prentice Hall College, 1984. |
| [38] | Forgacs G., Newman S.A. Biological Physics of the Developing Embryo, 346 p., Cambridge University Press, 2005. |
| [39] | Willmer E.N. Tissue culture: The growth and differentiation of normal tissues in artificial media, 126 p., Methuen & Co., 1935. |
| [40] | Gulati G., Caro J. Blood Cells An Atlas of Morphology with Clinical Relevance, 236 p., American Society for Clinical Pathology, 2007. |
| [41] | Biosurfactants: From Genes to Applications (Ed. by G. Soberon-Chavez), 223 p., Springer, 2010. |
| [42] | Kessin D.H. Dictyostelium: Evolution, Cell Biology, and the Development of Multicellularity, 308 p., Cambridge University Press, 2001. |
| [43] | Bonner J.T. The Social Amoebae: The Biology of Cellular Slime Molds, 156 p., Princeton University Press, 2008. |
| [44] | Sawyer R.H., Showman R.M. The Cellular and Molecular Biology of Invertebrate Development, 339 p., University of South Carolina Press, 1985. |
| [45] | Minelli A. Forms of Becoming: The Evolutionary Biology of Development, 242 p., Princeton University Press, 2009. |
| [46] | Keller E.F. Making Sense of Life: Explaining Biological Development with Models, Metaphors, and Machines, 400 p., Harvard University Press, 2003. |
| [47] | Sharpe J., Lumsden C.J., Woolridge N. In Silico: 3D Animation and Simulation of Cell Biology with Maya and MEL, 656 p., Morgan Kaufmann, 2008. |
| [48] | Deutsch A., Dormann S. Cellular Automaton Modeling of Biological Pattern Formation, 300 p., Birkhäuser Boston, 2004. |
| [49] | Ellner S.P., Guckenheimer J. Dynamic Models in Biology, 352 p., Princeton University Press, 2006. |
| [50] | Davies J. Mechanisms of Morphogenesis, 385 p., Academic Press, 2005. |
| [51] | Stewart I. Life's Other Secret: The New Mathematics of the Living World, 285 p., Wiley, 1999. |
| [52] | Pivar S. On the Origin of Form: Evolution by Self-Organization, 208 p., North Atlantic Books, 2009. |
| [53] | Pollack G.H. Cells, Gels and the Engines of Life, 320 p., Ebner & Sons, 2001. |
| [54] | Szemplinska-Stupnicka W., Iooss G., Moon F.C. Chaotic Motions in Nonlinear Dynamical Systems, 198 p., Springer, 1988. |
| [55] | Berg H.C. Random Walks in Biology, 164 p., Princeton University Press, 1993. |
| [56] | Mathematical Models for Biological Pattern Formation (Ed. by P.K. Maini, H.G. Othmer), 327 p., Springer, 2000. |
| [57] | Harrison L.G. The Shaping of Life: The Generation of Biological Pattern, 272 p., Cambridge University Press, 2011 |
| [58] | Fendler J.H. Membrane Mimetic Chemistry: Characterizations and Applications of Micelles, Microemulsions, Monolayers, Bilayers, Vesicles, Host-Guest Systems, and Polyions, 522 p., John Wiley & Sons, 1982. |
| [59] | Perthame B. Transport Equations in Biology, 206 p., Birkhäuser Basel, 2006. |
| [60] | Cell-Cell Channels (Ed. by F. Baluka, D. Volkmann, P.W. Barlow), 339 p., Springer, 2006 |
| [61] | Cell-Cell Junctions (Ed. by J.W. Nelson, E. Fuchs), 443 p., Cold Spring Harbor Laboratory Press, 2010 |
| [62] | Edelman G.M., Thiery J.-P. The Cell in Contact: Adhesions and Junctions as Morphogenetic Determinants, 516 p., Wiley, 1986 |
| [63] | Thom R. Structural Stability And Morphogenesis, 400 p., Westview Press, 1994. |
| [64] | Slack J.M. From Egg to Embryo: Regional Specification in Early Development, 352 p., Cambridge University Press, 1991. |
| [65] | Gradov O., Gradova M., Rybakov S., Choon S.J. Inorganic biomimetics for clinical hematology. Medical and Health Science Journal, Vol. 2, pp. 10 -17 (2010). |


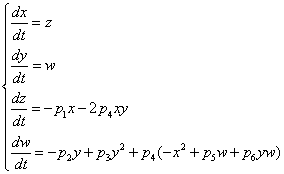
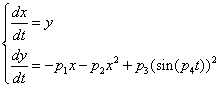


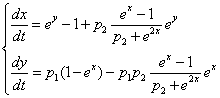
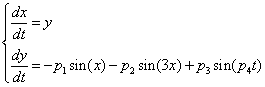
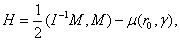

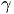 - unit vector vertical, r0 - radius vector of the center of mass,
- unit vector vertical, r0 - radius vector of the center of mass, 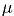 - body weight, I = diag (I1, I2, I3 - inertia tensor,
- body weight, I = diag (I1, I2, I3 - inertia tensor,  .
.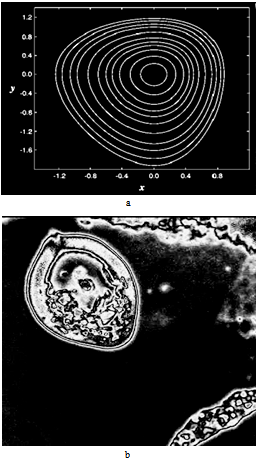
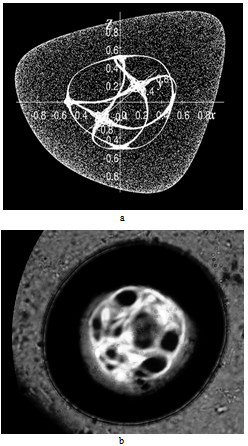
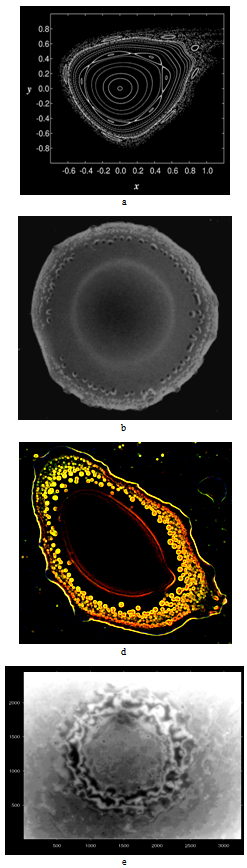
 = 0.5, I = diag (2,3,1), r0 = (1, 1, 0). This map, as well as the above equation of a polyharmonic pendulum, can approximate the shape of the cell colonies shown in Fig. 5c. Comparing the system of resonances (5b) and the phase portrait of polyharmonic pendulum (5a), one can conclude that the colony formation is due to cell division. The structure reminiscent of the Cassini ovals or their special case – lemniscate of Bernoulli (Fig. 5a) is a structure-approximant for the fission process of artificial cells. This finding is under a strong mathematical foundation.
= 0.5, I = diag (2,3,1), r0 = (1, 1, 0). This map, as well as the above equation of a polyharmonic pendulum, can approximate the shape of the cell colonies shown in Fig. 5c. Comparing the system of resonances (5b) and the phase portrait of polyharmonic pendulum (5a), one can conclude that the colony formation is due to cell division. The structure reminiscent of the Cassini ovals or their special case – lemniscate of Bernoulli (Fig. 5a) is a structure-approximant for the fission process of artificial cells. This finding is under a strong mathematical foundation.
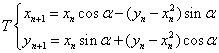
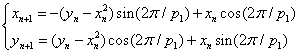
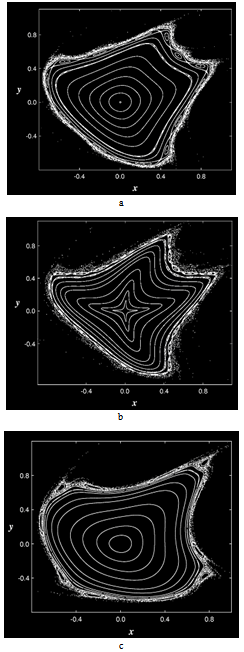

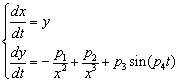

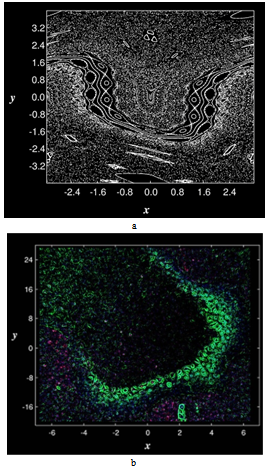
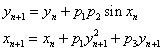
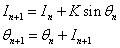
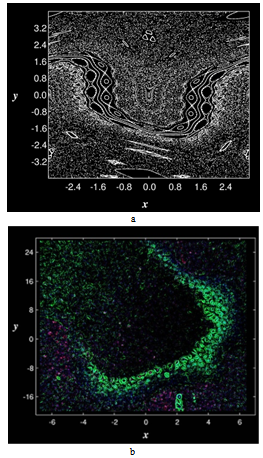

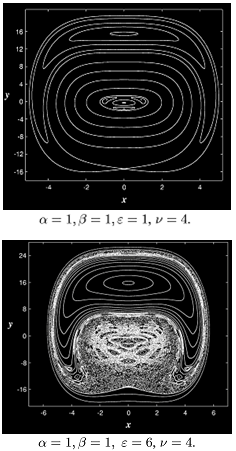
 - parameters and ε - a small parameter. These parameters theoretically lead to a specific type of invariant curves behaviour, which, in terms of morphology, forms the structures similar to embryonic sections in the early stages of morphogenesis - in particular, at the stage of gastrulation (Fig. 11 a, b).
- parameters and ε - a small parameter. These parameters theoretically lead to a specific type of invariant curves behaviour, which, in terms of morphology, forms the structures similar to embryonic sections in the early stages of morphogenesis - in particular, at the stage of gastrulation (Fig. 11 a, b). Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML