1. Introduction

The prevalence of diabetes is increasing in developed and developing countries. Roglic et al., 2005 estimated the global mortality due to diabetes at 2.9 million deaths that was equivalent to 5.2% of world all-cause mortality in the year 2000, that included 1 million deaths in developed countries and 1.9 million deaths in developing countries. Presenting the global health burden of diabetes, Wild et al, 2004 indicated that the human and economic costs of the growing diabetic epidemic would be very high, not only due to the increasing prevalence of diabetes, but also due to deaths due to the accompanying cardiovascular disease and other complications. In the estimates of world prevalence of diabetes in 2000 and projection for 2030, India, China, and the U.S. topped the list[1].

While age is regarded an independent risk factor for CVD, it is related with other risk factors that also increase with age, such as hypertension, hyperlipidemia, and diabetes[2]. Further, a combination of two or more risk factors increases the cardiovascular risk; for instance, patients with diabetes alone have twice the risk of myocardial infarction, but those with diabetes and hyperlipidemia have about a 15-fold increased risk. Hypertensive patients have twice the risk of myocardial infarction, however hypertensive patients with hyperlipidemia have approximately a 15-fold increased risk[2]. The results of the study in CVD-free type 2 diabetic patients by Avogaro et al[3] identified hyperglycemia, hypertension, and dyslipidemia, as significant risk factors that predispose the diabetics to development of coronary heart disease (CHD), and hence these risk factors have to be effectively controlled.

Connecting diabetes and CVDs is the metabolic syndrome, which may be considered as a group of risk factors of metabolic origin that increase the risk for cardiovascular disease and type 2 diabetes. These risk factors include atherogenic dyslipidemia, elevated blood pressure, elevated plasma glucose, a prothrombotic state, and a proinflammatory state[4]. The identification of this common cluster of risk factors may be beneficial for an integrated approach to reduce risk for both conditions simultaneously[5]. It is necessary for health care providers to control these risk factors to mitigate the development of CVD complications in diabetics, and to control diabetes. When diet regulation and exercise are found inadequate, effective drug therapy may be required to control the blood sugar, blood pressure and blood cholesterol levels, in diabetes.

A mathematical model based on ordinary differential equations (ODEs) was developed by Boutayeb et al. 2004[6] that discussed the diabetic population dynamics in the presence and absence of complications. Their mathematical study emphasized that controlling diabetes and its complications, was significant in health care management and its economics. In the present study, a mathematical model has been developed to examine the specific risk burden imposed by hypertension and hyperlipidemia in diabetic populations, towards developing cardiovascular complications. The model is also expected to reflect the extent of CVD prevention when these risk factors associated with diabetes were controlled.

2. Materials and Methods

In this section, we will describe the dynamics of CVD in a diabetic population with the risk burden of hypertension and hyperlipidemia, using ordinary differential equations (ODEs) [7 -13].

2.1. The Model

We consider a population that is divided into two distinct classes: Diabetic population and CVD population. In this model, we describe the dynamics of diabetics developing CVD with comorbidities - hypertension and hyperlipidemia. Let 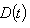denote the total population of diabetics at time t, and 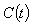be the total population of CVD patients at time t. Let 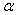denote the constant rate of inflow of diabetics into the diabetic class . Let 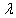be the constant rate of developing CVD due to Hypertension and 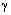be the constant rate of developing CVD due to Hyperlipidemia in the diabetic population. Let 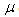denote the natural mortality rate of both the populations.

Thus, the rate of change of the diabetic population will be given by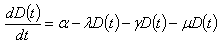

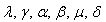Table 1. Parameters of the Diabetic-CVD model Parameters Description λ constant rate of developing CVD due to hypertension in the diabetic population. γ constant rate of developing CVD due to hyperlipidemia in the diabetic population. α constant rate of inflow of diabetics into the diabetic class β constant rate of inflow of CVD patients into the CVD class μ natural mortality rate of both the populations δ death rate of the CVD class due to the disease

where are positive constants.

Let 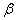denote the constant rate of inflow of CVD patients into the CVD class and 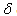denote the death rate of the CVD class due to the disease. Since, the loss in the diabetic class is the gain in the CVD class, the rate of change of CVD population will be given by

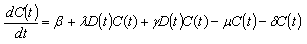Combining the two equations along with the initial conditions, the model is given by

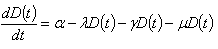(1)

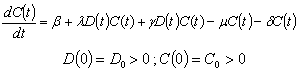(2)

2.2. The Steady States of the System

In this section, we compute the steady states of the model[14,15]. The system has only one equilibrium- positive equilibrium.

Set 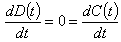we get

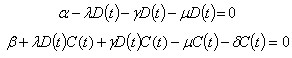Now solving the above, we get the positive equilibrium point as

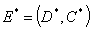where

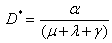
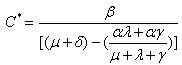Where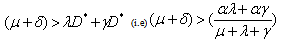

2.3. Stability of the Equilibrium Point

In this section, we will give some results on the stability of the equilibrium[14,15].

Theorem: The positive equilibrium 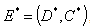, if it exists, is locally asymptotically stable.

Proof. We compute the jacobian matrix of the system about the equilibrium point. The jacobian matrix is given by

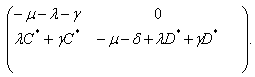The eigen values of the above matrix are

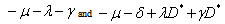Now, the equilibrium is locally asymptotically stable if and only if all the eigen values of the jacobian matrix have negative real parts. But, all the eigen values will have negative real parts, since from section 2.2, the positive equilibrium exists if and only if 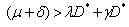(i.e) 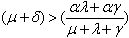. This proves the theorem.

3. Results

The present model is used for simulations based on data available in literature. The model has 6 parameters: 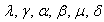. Tables 2 and 4 present the model parameters in various scenarios along with the diabetic population and the CVD population in equilibrium state.

Scenario 1 captures the condition where the inflow of new non-diabetic CVD patients is 0.12 % and the corresponding net death rate due to the disease is 0.05%. Another situation is depicted in scenario 2, where the rate of development of CVD due to non-diabetic factors is far lesser than scenario 1. Accordingly, the death rate due to the disease is also lesser. For this reason, the rate of inflow of CVD (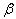) is assigned 0.05% and the death rate due to the disease (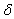) is 0.01%.

Table 3 gives the parameter values in scenario 1, where the HTN rate and HL rate are reduced by 50%, 75%, 87.5%, and 100% of the human population. The corresponding population of diabetics and the population of CVD in steady state are tabulated.

Table 4 gives the parameter values and the steady state populations in case of untreated comorbidities, in scenario 2

Table 5 gives the parameter values in scenario 2, where the HTN rate and HL rate are reduced by 50%, 75%, 87.5%, and 100% of the human population. The corresponding population of diabetics and the population of CVD in steady state are tabulated.

Table 3. Effect of treatment of comorbidities in Diabetic CVD cases α- inflow of diabetics β- inflow of CVD μ- natural mortality rate λ- HTN rate γ- HC rate δ- death rate due to CVD D*-steady state diabetic population C*-steady state CVD population % Decrease in CVD cases Hypertension and/or Hyperlipidemia controlled in 50% cases 0.2 0.12 0.66 0.29 0.29 0.05 0.1032 0.1846 7.059 0.2 0.12 0.66 0.58 0.15 0.05 0.1137 0.1914 3.634 0.2 0.12 0.66 0.29 0.15 0.05 0.0909 0.1791 9.816 Hypertension and/or Hyperlipidemia controlled in 75% cases 0.2 0.12 0.66 0.15 0.29 0.05 0.0909 0.1791 9.816 0.2 0.12 0.66 0.58 0.07 0.05 0.1084 0.1876 5.521 0.2 0.12 0.66 0.15 0.07 0.05 0.0636 0.1724 13.185 Hypertension and/or Hyperlipidemia controlled in 87.5% cases 0.2 0.12 0.66 0.07 0.29 0.05 0.0824 0.1764 11.188 0.2 0.12 0.66 0.58 0.04 0.05 0.1063 0.1863 6.193 0.2 0.12 0.66 0.07 0.04 0.05 0.0442 0.1702 14.31 Hypertension and/or Hyperlipidemia controlled in 100% cases 0.2 0.12 0.66 0 0.29 0.05 0.0737 0.1743 12.256 0.2 0.12 0.66 0.58 0 0.05 0.1032 0.1846 7.059 0.2 0.12 0.66 0 0 0.05 0.0182 0.169 14.896

Table 4. Untreated Comorbidities in Diabetic CVD α- inflow of diabetics β- inflow of CVD μ- natural mortality rate λ- HTN rate γ- HL rate δ- death rate due to CVD D*-steady state diabetic population C*-steady state CVD population 0.2 0.05 0.66 0.6 0.5 0.01 0.1716 0.1039

Table 5. Effect of treatment of comorbidities in Diabetic CVD cases α- inflow of diabetics β- inflow of CVD μ- natural mortality rate λ- HTN rate γ- HL rate δ- death rate due to CVD D*-steady state diabetic population C*-steady state CVD population % Decrease in CVD cases Hypertension and/or Hyperlipidemia controlled in 50% cases 0.2 0.05 0.66 0.3 0.5 0.01 0.1658 0.093 10.448 0.2 0.05 0.66 0.6 0.25 0.01 0.1669 0.0947 8.879 0.2 0.05 0.66 0.3 0.25 0.01 0.1587 0.0858 17.414 Hypertension and/or Hyperlipidemia controlled in 75% cases 0.2 0.05 0.66 0.15 0.5 0.01 0.1618 0.0885 14.794 0.2 0.05 0.66 0.6 0.13 0.01 0.164 0.0909 12.541 0.2 0.05 0.66 0.15 0.13 0.01 0.1468 0.0795 23.477 Hypertension and/or Hyperlipidemia controlled in 87.5% cases 0.2 0.05 0.66 0.08 0.5 0.01 0.1597 0.0866 16.650 0.2 0.05 0.66 0.6 0.07 0.01 0.1624 0.0891 14.244 0.2 0.05 0.66 0.08 0.07 0.01 0.1383 0.077 25.877 Hypertension and/or Hyperlipidemia controlled in 100% cases 0.2 0.05 0.66 0 0.5 0.01 0.1569 0.0845 18.646 0.2 0.05 0.66 0.6 0 0.01 0.1603 0.0871 16.131 0.2 0.05 0.66 0 0 0.01 0.1242 0.0746 28.172

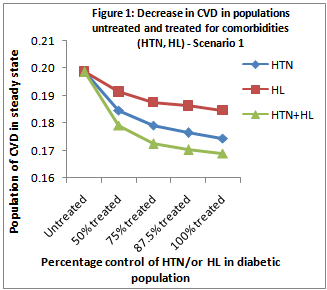Figure 1. depicts the trend in scenario 1

The other aspect that we have differed in both the scenarios is, with respect to the relative prevalence of HTN and HL. In scenario 1, the prevalence of HTN in diabetics is far higher than the prevalence of HL in diabetics (0.58% vs 0.29%), while in scenario 2, the prevalence of HTN and HL in diabetic population is similar (0.6% vs 0.5%).

The impact of controlling the diabetic co-morbidities, hypertension and hyperlipidemia, on the development of CVD, is presented in tables 3 (scenario 1) and 5 (scenario 2). Here, the effect on CVD reduction has been compared between the control of one of the two risk factors at a time, with the simultaneous control of both the risk factors. Figures 1 and 2 clearly demonstrate the decrease in diabetic CVD population (at steady state) when the risk factors, hyperlipidemia and hypertension, are controlled (clinically treated) in scenarios 1 and 2 respectively.

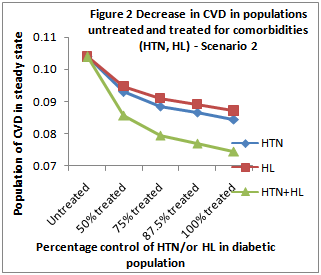Figure 2. presents the trend in scenario 1

4. Discussion

Here, a mathematical model has been developed to study the impact of two important risk factors hypertension and hyperlipidemia, in diabetic CVD. Different scenarios that emerged with varying of the values of the test parameters suggested the extent of control of CVD in diabetic patients.

It is well known that there is a global rise in incidence of diabetes and CVD. The existence of comorbidities such as hypertension and hyperlipidemia in diabetics is often not detected, or not adequately managed. Hence, despite the control of hyperglycemia in diabetics, this population still remains a potential candidate for developing CVD[16] concluded from their study on Bangladeshi patients with diabetes that controlling central obesity, dyslipidemia, and hypertension may decrease the prevalence of the metabolic syndrome that in turn would decrease the incidence of cardiovascular events[16].

In this context, a mathematical approach was adopted to evaluate the risk burden of CVD complications in diabetics with untreated co-morbidities (HTN & HL). A model based on ODEs has been developed which describes the dynamics of CVD risk in a diabetic population with hypertension and hyperlipidemia. The numeric values for some of the parameters in the model have been chosen closer to actual reported values from clinical or epidemiologic studies reported in literature[17, 18]

The biological relevance of the mathematical model developed here is substantiated by the following facts: (1) the model yields positive equilibrium under the given conditions, (2) the impacts of intervention is reflected in the model. The present analysis indicates:

(1) Decrease in CVD population when either HL or HTN is controlled in diabetics

(2) Marked decrease (greater than control of either of the co-morbidities) in CVD development in diabetics when both HTN & HL are controlled.

In scenario 1, when HTN is controlled in 50% of the population, the percentage decrease in CVD population is about 7%, which further decreases to around 12% when all hypertensives are treated. In scenario 2, the reduction in diabetic CVD population when all hypertensives (100%) are treated is nearly two-fold, when compared with the diabetic population where only 50% hypertensive cases are treated (19% vs 10%). Perreault et al., 1999[19] pointed out that in hypertensives, owing to the co-existence of several coronary artery disease (CAD) risk factors including increased age, dyslipidemia, diabetes mellitus, obesity and sedentary lifestyle, it is necessary to screen for and treat the modifiable risk factors such as hyperlipidemia and obesity, in addition to controlling blood pressure, in order to reduce the risk of cardiovascular morbidity and mortality.

In the present analysis, when hyperlipidemia is controlled in 50% of the diabetic population, a 3% decrease in CVD is observed. This decrease in CVD is further enhanced in conditions where all HL patients have been treated (about 7%). A similar trend is seen in scenario 2 (about 9% vs 16%).

When both the co-morbidities are treated in 50% of the population, we observe around 10% and 17% decrease in CVD development in scenarios 1 and 2 respectively. When all (100%) the hypertensive and hyperlipidemic diabetics are treated for both HTN and HL, the percentage decrease in CVD population obtained in this mathematical model is obtained is 15%, and 28% respectively in scenarios 1 and 2 respectively.

In comparison with control of one of the risk factors at a time, if both the co-existing risk factors are controlled, the extent of bringing down the CVD incidence in diabetics is substantially improved. For instance, in scenario 2, when all the diabetics with hypertension are treated for their blood pressure, the CVD incidence decreases by 19%, and when the diabetic hyperlipidemia alone is treated in 100% cases, the CVD incidence decreases by 16% in the present model. However, in the same scenario when both the co-existing risk factors, HTN and HL, are treated in all the cases (100%), the impact of decreasing the CVD burden is found to be 28%. Taken together, these results suggest a drastic reduction in the number of diabetics developing CVD when their co-morbid risk factors are effectively treated.

In scenario 2 of the present model, the risk imposed by diabetes to the development of CVD has been accentuated by keeping the inflow into diabetes population same as scenario 1, yet reducing the inflow of non-diabetic CVD cases. Additionally, the percentage population having hyperlipidemia has been raised to 0.50 in scenario 2 (compared to 0.29 of scenario 1), which is also closer to percentage population having hypertension (0.60). In a study conducted in some representative samples in four cities in central Argentina, the prevalence was in the range 27.9% 43.6% for hypertension, 24.2% 36.4% for hyperlipidemia, and 6.5% and 7.7% for diabetes mellitus, where 51.2% of the diabetics had hypertension and 52.8% of the diabetics had hyperlipidemia[18].

These results not only indicate the risk burden imposed by hyperlipidemia and hypertension in diabetic population, but also point to the importance of CVD prevention strategies in diabetes populations. In diabetics, while control of blood glucose levels always remains on high priority in clinical management, the need for effective anti-hypertensive and lipid-lowering therapy is emphasized, to prevent this population from the development of CVD[20]. For this, firstly, the presence of co-morbidities (hypertension and/or hyperlipidemia), will have to be diagnosed in the diabetic patient. Hypertension, a risk factor that is amenable to therapy, was reported in 40% diabetics in a study in India[21]. Diagnosing and controlling hypertension is particularly significant in diabetic patients, as it would greatly decrease the risk of CVD and the associated morbidity and mortality[21].

Grundy et al.[5] analysed the CVD complications in diabetes, and suggested guidelines for the prevention of CVD in diabetics through control of risk factors, with a more aggressive management of blood cholesterol levels in the diabetics (compared to non-diabetics). Diabetics CVD patients are reported to have a poor prognosis for survival relative to non-diabetic CVD patients.[5]. In their study during the period 1998 to 2004, it was found that there was some improvement in managing hypertension and hyperlipidemia in type 2 diabetes patients. However, they also observed that still greater efforts were needed towards medication adjustments in patients with insufficiently controlled hypertension and combined risk factors, in terms of intensifying the treatment, or increasing dosages when the co-morbid risk factors were uncontrolled in the diabetic patients.

To conclude, the analysis of the bio-mathematical model developed here clearly illustrates the reduction in CVD incidence in population with diabetes when the accompanying risk factors, hyperlipidemia and hypertension, are controlled. These results further emphasize the need for early diagnosis and effective treatment of abnormal blood pressure and blood lipid levels in diabetes condition. This would in part, prevent the immigration of the population with diabetes into another major disease category of CVDs.

ACKNOWLEDGEMENTS

The work was supported by the research grant from the University Grants Commission (UGC), New Delhi, India.