1. Introduction

Artificial Immune Systems (AISs) represent a field of biologically inspired computing that attempts to exploit theories, principles, and concepts of modern immunology to design immune system-based applications in science and engineering[1–3]. The IS provides an excellent example of a bottom up intelligent strategy[4], through which adaptation operates at the local level of cells and molecules, and useful behavior emerges at the global level: this is exemplified by the immune humeral and cellular responses.

AISs are proving to be a very general and applicable form of bio-inspired computing. A great deal of work has gone into developing algorithms that extrapolate basic immune processes such as clonal selection, negative and positive selection, danger theory, and immune networks[2]. To date, AIS have been applied to areas such as machine learning[5],[6], optimization[7],[8], bioinformatics[9 –11], robotic systems[12–14], decision support systems[15], network intrusion detection[16],[17], combinatorial optimization[18],[19] and scheduling[20],

Given the primary sequence of a protein, the protein structure prediction problem requires the identification of its native (tertiary) conformation with minimum energy; while the protein folding problem requires information about the possible pathways to folding and unfolding. Since a protein’s structure determines its biological function, it is very important to be able to predict the final spatial conformation of the proteins.

In this work, the standard HP lattice bead model has been incorporated into an immune algorithm. Despite the minimalistic approach employed by this model, it has been shown to belong to the “NP-Hard” set of problems, and many approximation methods and heuristics have been investigated to address it[21]. Existing computing approaches to PSP include evolutionary search[22-25], ant colony optimization[26], memetic algorithms[27], tabu search[28] and Monte Carlo algorithms[29].

The potential energy of a molecule is derived from molecular mechanics, whichdescribes molecular interactions based on the principles of Newtonian physics. Anempirically derived set of potential energy contributions is used for approximatingthese molecular interactions.This set of potential energy contributions, called theforce field, contains adjustableparameters that are selected in such a way as toprovide the best possible agreementwith experimental data. Our discussion will focuson energy functions which sharethe main features of general molecular force fields.The molecular model considered here consists of a chain of m atoms centered at in a 3D space, as seen in Figure 1. For every pair of consecutive atoms x_i and, let be the bond length which is the Euclidean distance between them. For every three consecutive atoms x_i, , 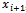let be the bond angle corresponding to the relative position of the third atom with respect to the line containing the previous two. Likewise, for every four consecutive atoms 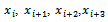let 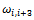be the angle, called the torsion angle, between the normal through the planes determined by the atomsand The force field potentials corresponding to bond lengths, bond angles, and torsion angles are defined respectively[30] as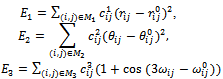

(1)

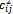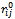whereis the bond stretching force constant, is the angle bending force constant, and is the torsion force constant. The constant and 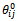represent the “preferred” bond length and bond angle, respectively, and the constant 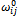is the phase angle that defines the position of the minima. The set of pairs of atoms separated by k covalent bond is denoted byfor k = 1, 2, 3. In addition to the above, there is a potential 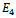which characterizes the 2-body interaction between every pair of atoms separated by more than two covalent bonds along the chain. We use the following function to represent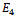

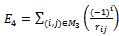(2)

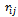where is the Euclidean distance between atoms 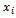and.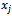

The general problem is the minimization of the total molecular potential energy function, , leading to the optimal spatial positions of the atoms. To reduce the number of parameters involved in the potentials above, we simplify the problem considering a chain of carbon atoms. In this case, it is known that the preferred bond lengths are= 1.526°A (for all and that the bond angles are for all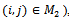, we consider also that 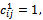for all for all 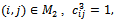for all 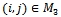and for all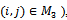, While this structure reflects great simplifications over the general problem, its complexity should not be underestimated, as we will see below.

In most molecular conformational predictions, all covalent bond lengths and covalent bond angles are assumed to be fixed at their equilibrium values and respectively. Thus, the molecular potential energy function reduces to 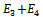and the first three atoms in the chain can be fixed. The first atom,x₁ ,is fixed at the origin, (0, 0, 0); the second atom,x₂ , is positioned at 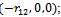and the third atom, x₃, is fixed at 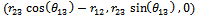Using the parameters previously defined and Eq.(1) and Eq.(2), we obtain

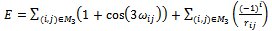(3)

Although the molecular potential energy function (3) does not actually model the real system, it allows one to understand the qualitative origin of the large number of local minimizers, the main computational difficulty of the problem[31]. Note that, Eq.(1), is expressed as a function of torsion angles, and E₄ , Eq.(2), is expressed as a function of Euclidean distance. To represent Eq.(3) as a function angles only, we can use the result established in[32] and obtain

(4)

Finally we can express the potential energy as function of the torsion angles.as Eq.(5)

(5)

where,

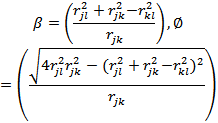and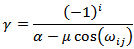

where i= 1, . . . ,m − 3 and m is the number of atoms in the given system as seenin Figure 1.

Despite these simplification, the problem remains very difficult. A molecule with as few as 30 atoms has 227 = 134, 217, 728 local minimizers. It can clearly beseen that finding the global minimum for chains of even moderate length is intractable via exhaustive methods[33].

Figure 1. Coordinate Set of Atomic Chain

2. Llattice model HP for the PSP

In this work, the standard HP lattice bead model is embedded in a 2-dimensional square lattice, restricting bond angles to only a few discrete values. Interactions are only counted between topological neighbours, that is between beads (representing amino acids) that lie adjacent to each other on the lattice, but which are not sequence neighbours . The energies corresponding to the possible topological interactions are as follows: 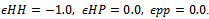By summing over these local interactions, the energy of the model protein can be obtained:

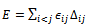(6)

Where

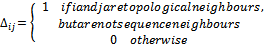The HP lattice model recognizes only the hydrophobic interaction as the driving force in protein folding, with many native structures protecting the hydrophobic core with polar residues, resulting in a compact arrangement[34].

Table 1. Benchmark HP sequences used in the present study[35]. The lowest energies that have been found for these sequences are indicated by E*

3. The Immune Algorithm

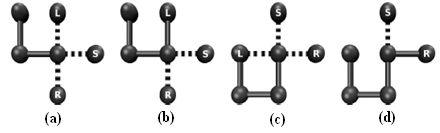
An immune algorithm[36] is inspired by the clonal selection principle employed by the human immune system. In this process, when an antigen enters the body, B and T lymphocytes are able to clone upon recognition and bind to it[36]. Many clones are produced in response and undergo many rounds of somatic hypermutation. The higher the fitness of a B cell to the available antigens, the greater the chance of cloning. Cells have a certain life expectancy, allowing a higher specific responsiveness for future antigenic attack[34] .

The IA presented here includes the aging, cloning and selection operators used in a previous study by Cutello et al.[34], with modified constructor and mutation operators. The constructor employs a backtracking algorithm that records some of the possible mutations by testing bead placement during chain growth. These possibilities are exploited and updated during the mutation process, preventing an infeasible conformation from occurring based on the preceding self-avoiding structure for a particular point in the model protein chain. In retaining this information, infeasible mutations are not explored, allowing a greater number of constructive mutations to be investigated. Figure 2 illustrates the stages involved in placing two consecutive beads during the chain growth phase. Before committing a bead to the lattice, all possible directions are explored, Figure 2(a), and from the valid options available, a random choice is made, Figure2(b). Again all possible choices are investigated, marking any infeasible options (note that choosing left will not result in a self avoiding conformation), Figure2(c), and a valid choice is selected from the remaining options, Figure 2(d).

Any remaining valid choices are left unmarked for use in the first mutation phase after the initial chain growth. Once a valid mutation has been made, the entire structure is reconstructed as before marking any infeasible directions as a result of the new conformation vector.In the basic IA set up, there are a maximum of 1,000,000 fitness evaluations, with the maximum number of generations set to 50,000. In order to estimate the optimal combination of parameters, we adopted the procedure used by Cutelloet al., whereby the maximum Bcell age and the number of clones were each varied from 1 to 10. Population sizes examined were 10, 25, 50, 100 and 200. This provided a combination of 500 different parameter sets for each sequence, which was applied to allthe benchmark sequences up to 25 beads in length. All fitness evaluations for the best success rates were collated and graded for overall performance. As a result of this preliminary testing, the results presented below were obtained using a maximum B-Cell age of 4, 3 clones and a popu

Figure 2. Stages of the chain growth algorithm investigating left (L), right (R) and straight (S) availability (a), random selection from all available directions (b), at the next locus investigation of L, R and S availability (c) and random selection from remaining available S and R directions (d)

The theory of clonal selection , suggests that B and T lymphocytes that are able to recognize the antigen, will start to proliferate by cloning upon recognition of such antigen. When a B cell is activated by binding an antigen (and a second signal is received from T lymphocytes), many clones are produced in response, via a process called clonal expansion. The resulting cells can undergo somatic hypermutation, creating offspring B cells with mutated receptors. The higher the affinity of a B cell to the available antigens, the more likely it will clone.

This results in a Darwinian process of variation and selection, called affinity maturation. The increase in size of these populations couples with the production of cells with longer than expected lifetimes, assuring the organism a higher specific responsiveness to that antigenic attack in the future. This gives rise to immunological memory which is demonstrated by the fact that, when the host is first exposed to the antigen, a primary response is initiated; in this phase the antigen is recognized and immune memory is developed. When the same antigen is encountered in the future, a secondary immune response is initiated. This results from the stimulation of cells already specialized and present as memory cells: a rapid and more abundant production of antibodies is observed. The secondary response can be elicited from any antigen that is similar, although not identical, to the original one that established the memory. This is known as cross-reactivity.

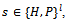The proposed IA employs two entity types: antigens (Ag) and B cells. The Ag models the hydrophobic-pattern of the given protein, that is a sequence where lis the protein length, i.e., the number of amino acid in the protein sequence, whereThe B cell population, 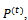represents a set of candidate solutions in the current fitness landscape at each generation t. The B cell, or B cell receptor, is a sequence of directions 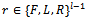(with L=Left, R=Right and F= Forward), where eachr_i , with is a relative direction with respect to the previous direction (i.e., there are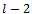 relative directions) and 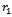the nonrelative direction.Hence, we obtain an overall sequence of length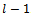. The sequence r specifies a 2-D conformation which is suitable for computing the energy value of the hydrophobic-pattern of the given protein. At each generation t , there is a B cell population of 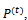size d. The initial population, time t=0, is randomly generated in such a way that each B cell of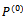, is a self-avoiding conformation. There are two main functions within the algorithm. Evaluate(P) which computes the fitness function value of each B cell; hence 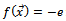is the energy of conformation coded in the B cell receptor ; and Termination_Condition()which returns true if a solution is found, or a maximum number of fitness function evaluations 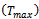is reached. The implemented IA, like all IAs based on the clonal selectionprinciple outlined above, is characterized by cloning of B cells with higher antigenic affinity, affinity maturation, and hypermutation of offspring B cells.

4 Results

4.1. Algorithm Comparison

With CPU time being hardware dependent, the number of fitness evaluations (together with the percentage success rate) has been used to assess the efficiency of the algorithm, as shown in Table 2 for the benchmark sequences. It is apparent from Table 2 that, although the use of memory B-Cells[34] hinders the discovery of global minima for some of the smaller sequences, it enhances the search forthe larger, more difficult to find sequences. The memory ability allows mid to high fitness conformations to remain in the population for a longer number of generations. For larger sequences, this allows a more detailed exploration in certain areas of the potential energy surface, permitting thememory B-Cells to converge towards the global solution much sooner.

In contrast, for smaller sequences the mid to high fitness range is much smaller, thereby preventing a rapid exploration of the potential energy surface by retaining unfavorable segments of local structure for a largernumber of generations. Generally, the use of memory Bcells allows a more diverse inspection of the potential energy surface, due to a greater number of the degenerate conformations being found. This is achieved as favourable fragments of local structure are not rapidly disposed of during the retirement process, hindering efficiency as a consequence. The algorithm presented here shows promising results,being comparable to the work of Cutelloet al.[34]. While our success rates for the larger sequences (e.g. HP-48) are a little lower, in some cases our numbers of fitness evaluations show an improvement.

The compact structural arrangement present in all globalminima (GMs) is apparent from the example GMs shown in Figure3. With the driving force being the hydrophobic topological contact, it can be seen that compact hydrophobiccores give rise to high fitness conformations. Inspection of the HP-48 global minimum (i) allows us to understand the poor success rate for this sequence. The 5x5 hydrophobic core presents a problem to the IA in achieving convergence, as a single misplaced hydrophobic bead will result in only a metastable conformation. The problem does not exist for the HP-50 sequence (j), due to the presence of two small hydrophobic cores coupled by a chain of hydrophobic beads, which explains the higher success rate and fewer average structure evaluations necessary for HP-50, compared with HP- 48 and (when using memory B-cells) even the much shorter HP-36 sequence . The work of Cutello et al. supports this idea[34], as similar magnitudes of the number of fitness evaluations for these problematic sequences can be seen, with a much lower success rate for HP-48 than for any other instance

Table 2. Comparison of the percentage success and average number of structure evaluations with and without using memory B-Cells sequence l No Memory B Cell No Memory B Cell Success % No. Evaluation Success % No. Evaluation HP-18a 18 100 89578 100 117251 HP-18b 18 100 40167 100 200740 HP-18c 18 100 87761 100 72270 HP-20a 20 100 26207 100 312405 HP-20b 20 100 15221 100 30414 HP-24 24 100 26580 100 49616 HP-25 25 100 79042 100 95123 HP-36 36 63 4867993 90 3082014 HP-48 48 3 6318721 3 4195086 HP-50 50 50 4904031 96 853706 HP-60 60 46 5965234 47 8569230 HP-64 64 41 6589563 42 7589685

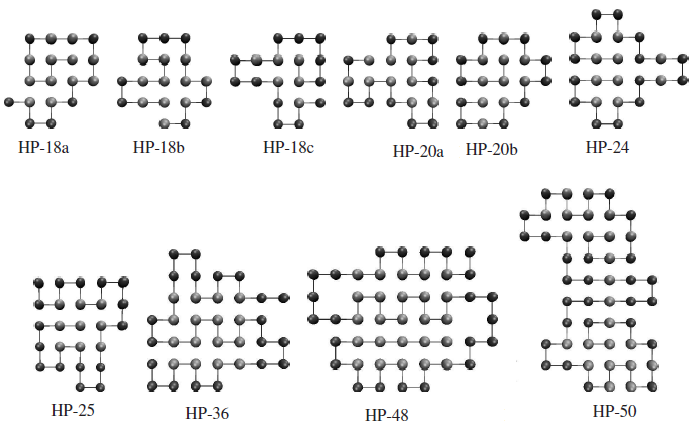Figure 3. Examples of GM structures for the benchmark sequences

Table3. Comparison of results achieved by different evolutionary methods for the HP problem sequence l E* GA[36] PMGA[37] MMA[27] EDAs[38] IA S1 1H 1P 1H 2P 2H 1P 1H 2P 1H 1P 2H 2P 1H 1P 1H 20 -9 -9 -9 -9 -9 -9 S2 2H 2P 1H 2P 1H 2P 1H 2P 1H 2P 1H 2P 1H 2P 2H 24 -9 -9 -9 -9 -9 S3 2P 1H 2P 2H 4P 2H 4P 2H 4P 2H 25 -8 -8 -8 -8 -8 -8 S4 3P 2H 2P 2H 5P 7H 2P 2H 4P 2H 2P 1H 2P 36 -14 -14 -14 -14 -14 -14 S5 2P 1H 2P 2H 2P 2H 5P 10H 6P 2H 2P 2H 2P 1H 2P 5H 48 -23 -22 -22 -22 -23 -23 S6 2H 1P 1H 1P 1H 1P 1H 1P 4H 1P 1H 3P 1H 3P 1H 4P1H 3P 1H 3P 1H 1P 4H 1P1H 1P 1H 1P 1H 1P 1H 1H 50 -21 -21 -21 -21 -21 -21 S7 2P 3H 1P 8H 3P 10H 1P 1H 3P 12H 4P 6H 1P 2H 1P1H 1P 60 -36 -34 -34 -35 -35 S8 12H 1P 1H 1P 1H 2P 2H 2P 2H 2P 1H 2P 2H 2P 2H 2P1H 2P 2H 2P 2H 2P 1H 1P1H 1P 12H 64 -42 -37 -38 -39 -42 -40

4.2. Comparisons with Other Evolutionary Algorithms

The results of the proposed algorithm for the HP instances are directly compared to the best results obtained by the following related evolutionary models: the results of standard GA[36], Pull-Move GA (PMGA)[37], multimeme algorithms (MMA)[27], and estimation of distribution algorithms (EDAs)[38]. The results of GA[36] are based on a population of 200 structures evolved over 300 generations

Table 3 presents the known optimum for each protein instance and the energy values found by each of the compared methods. A direct comparison between energy values obtained by the different evolutionary models emphasizes a good and competitive performance of the proposed ELF method. The results are clearly better than those reported by GAs[36] and PMGAs[37]. PMGA[37] is included in the comparative analysis as it is an evolutionary algorithm using pull move transformations in addition to the standard genetic operators (pull moves are not applied in a hill-climbing mode like in the IA and a specialized fitness function is used). PMGA improves the results of standard GAs for PSP but reports worse results for sequences S5, S7 and S8 compared to IA. MMAs represent an interesting approach to be compared with IA as both models use local search but according to different strategies. Results indicate a better solution obtained by IA for instance S5 when compared to MMA. This is a promising result for the proposed method underlying the good performance of hill-climbing crossover and pull-moves. Furthermore, the results of IA are competitive with those reported by recently proposed algorithm EDA. For sequence S7, IA obtains same global best energy of −35 while for sequence S8, IA is able to identify a higher energy conformation compared to other but does not detect the known optimum energy configuration as EDA.

5. Conclusions

Although implementation of a modified constructor for usein the mutation phase of the IA has not always given greatersuccess rates (especially for more challenging sequences),it has allowed for a more efficient search to be performedin some cases, showing a decrease in the number of fitnessevaluation performed. The use of population diversitytracking allows a greater understanding of the algorithm’sability to explore areas of the potential energy surface ofthese simple model proteins. Areas of favourable localstructure along the chain can be assessed, illustrating theimportant allele combinations that give rise to the determinationof global minima. We are currently applying theseapproaches to more realistic protein models