-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Bioinformatics Research
2012; 2(3): 11-20
doi: 10.5923/j.bioinformatics.20120203.01
Pharmacophore Modeling and Docking Based QSAR Studies of Aryl Amidino Isoxazoline Derivatives to Design Potential FXa Inhibitors
Suresh B Vepuri 1, S. Anbazhagan 2, Naresh P 1, D. Divya 1
1Institute of Pharmacy, GITAM University, Vishakapatnam, AP, 530045, India
2Karuna College of Pharmacy, Thirumittacode, Palakad, Kerala, 679533, India
Correspondence to: Suresh B Vepuri , Institute of Pharmacy, GITAM University, Vishakapatnam, AP, 530045, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
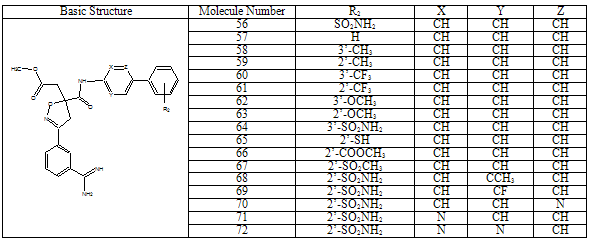
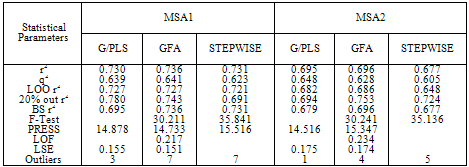
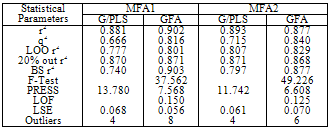
In order to elucidate the structural requirements for human factor Xa receptor antagonism, 72 antagonists belonging to isoxazolidine chemical class were selected from the literature and conducted molecular modeling studies. Best binding conformations were isolated by docking selected molecules into the receptor binding site. To further explore the structure-activity relationships within the considered chemical class, a pharmacophore model and QSAR analyses were developed. Pharmacophore models of these inhibitors were established by using the HipHop and HypoGen algorithms implemented in the Catalyst software package. The best quantitative pharmacophore model, which has the highest correlation coefficient (0.92), consisted of two hydrogen bond donor, a hydrophobic aromatic, and a ring aromatic feature. The model was further validated by test set and cross validation method. Molecular shape analysis (MSA) and Molecular field analysis (MFA) were used as the QSAR techniques. Two conformer-based alignment strategies were employed to construct reliable 3D-QSAR models. The docked conformer-based alignment strategy gave the best 3D-QSAR models. The best MFA and MSA models gave a cross-validated coefficient q(2) of 0.641 and 0.816, non-cross-validated r(2) values of 0.736 and 0.902, 20% out r(2) values of 0.743 and 0.871, respectively. The information obtained from molecular modelling studies was very helpful to design some novel selective inhibitors of factor Xa with desired activity.
Keywords: Catalyst, Factor Xa, Ligandfit, MSA, MFA, Pharmacophore and QSAR
Article Outline
1. Introduction
- Over the past twenty to thirty years, scientists have used computer models of new chemical entities to help define activity profiles, geometries and reactivities[1]. Computational chemistry/molecular modeling is the science (or art) of representing molecular structures numerically and simulating their behavior with the equations of quantum and classical physics[2]. The computational approaches used to design the drugs are dependent upon the amount of information that is available about the ligand and receptor. Based on the information that is available, one can apply either structure-based or ligand-based molecular design methods[3]. To discover novel ligands for receptors of known structure, investigators often use docking computer programs to screen multi-compound databases for molecules that fit a binding site on the receptor. Ligandfit[4] is one of such a drug discovery software program. QSAR and pharmacophore techniques are ligand-based approaches used to correlate the biological activity with chemical structure of ligands. In QSAR studies, quantitative correlation of molecular structures with the activity/property, and subsequently, the prediction of this property for novel compounds is done. Furthermore, these methods help to characterize those spatial features that are responsible for activity changes in a series of active molecules[5]. Molecular Field Analysis (MFA)[6] and Molecular Shape Analysis (MSA)[6] are two different modules of QSAR study. MFA quantifies the interaction energy between a probe molecule and a set of aligned target molecules in a QSAR. Interaction energies measured and analyzed for a set of 3D structures can be useful in establishing QSARs whereas, MSA extends QSAR operations for performing 3D QSAR studies. This technique generates quantitative measurements of molecular shape properties as part of QSAR analysis[6]. Statistical methods are an essential component of QSAR work. They help to build models, estimate a model's predictive abilities, and find relationships and correlations among variables and activities. Regression methods are used to build a model in the form of an equation that gives one or more dependent variables (usually activity) in terms of independent variables ("descriptors"). The model can then be used to predict activities for new molecules, perhaps prioritizing or screening a large group of molecules whose activities are not knownA pharmacophore is defined as an ensemble of universal chemical features that characterize a specific mode of action of a ligand in the active site of the macromolecule in 3D space[7]. Chemical features are e.g. hydrogen bonds, charge interactions, hydrophobic areas. CATALYST[8] is a pharmacophore generating modeling tool. It has been used successfully, in conjunction with traditional research techniques, to examine the structural properties of existing compounds, develop and quantify a hypothesis which relates these properties to observed activity and utilize these "rules" to predict properties and activities for new chemical entities[8]. Catalyst tools help to rationally design small molecules as drug candidates using 3D pharmacophore and shape-based models, and to suggest potentially active compounds suitable for synthesis and biological testingThe clinical usefulness of anticoagulants such as warfarin (Coumadin) and low molecular weight heparins (LMWHs) have generated a great interest in searching for new anticoagulants for the treatment and prevention of thromboembolic diseases. However, warfarin is an indirect inhibitor of blood coagulation and takes several days to reach effective anticoagulant levels[9]. LMWH requires a physiological cofactor, antithrombin III, to inactivate factor Xa (fXa). Therefore, the current drug discovery research focuses on designing small molecule inhibitors that directly act on coagulation factors such as thrombin and fXa. The direct thrombin inhibitors have shown good antithrombotic efficacy in animal thrombosis models. However, it is not certain whether the antithrombotic effects of these inhibitors can be achieved without bleeding complications in humans[10]. The alternative target of new anticoagulants is inhibition of the earlier sites of the coagulation cascade such as fXa. Factor Xa (fXa), a trypsin-like serine protease, is a critical enzyme which in combination with fVa and Ca2+ on a phospholipid surface forms the prothrombinase complex that converts biologically inactive prothrombin to thrombin. The activation of thrombin by fXa is a highly amplified process. Because of its central position at the convergent point of the intrinsic and extrinsic pathways of coagulation it is believed that inhibition of fXa may reduce the production of thrombin by either the extrinsic or intrinsic pathways without interfering with a basal level of thrombin activity necessary for normal hemostasis. The present study involves estimation of structure–activity relationship of aryl amidino isoxazoline derivatives which were reported as fXa inhibitors. This study would help in the rational development of new, synthetic, potent fXa inhibitors since it gives an insight into structural requirements for this series of inhibitors with the help of different QSAR methods.
2. Materials and Methods
2.1. Docking
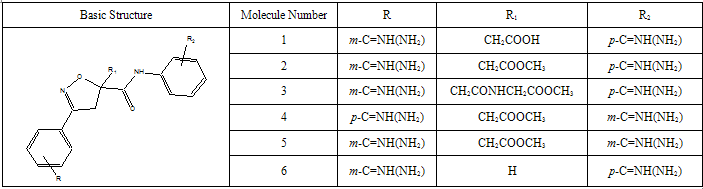
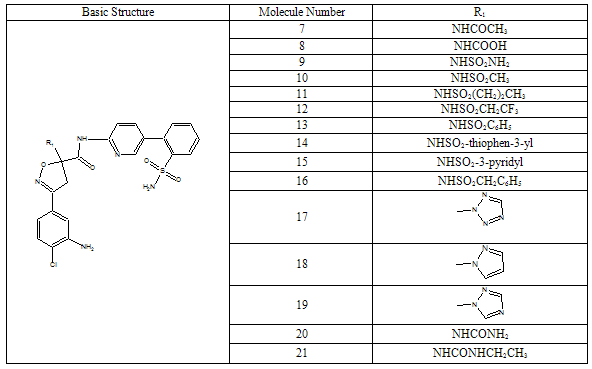
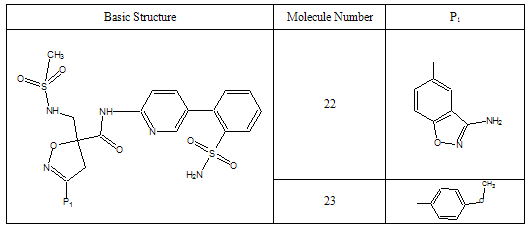
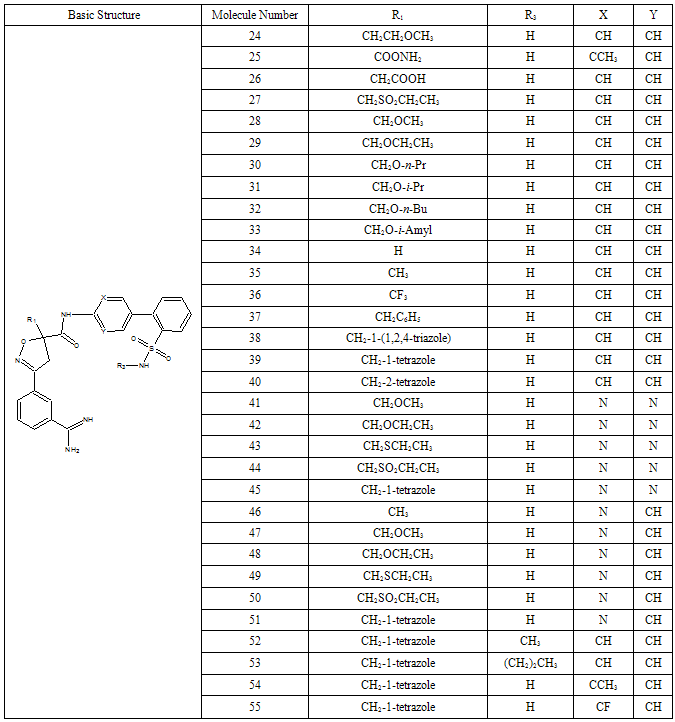
- All docking studies were performed using Accelrys Ligandfit installed on a Silicon Graphic Octane desktop Workstation. Shape and volume of the active site has been identified by selecting the aminoacid residues around the non stranded residue of the protein at 5 Ao distance. A set of aryl amidino isoxazoline derivatives from literature was used in this study[11-15] (Table-1 to Table-5). Ten Molecules with varied range of activities were selected from the study set molecules. Conformational search on each selected molecules was done by simplex search method. Generated conformers were docked in the active site and calculated for their interactions. Ten best conformations for each molecule were selected by the system based on dock score and ligand interaction energies.
2.2. 3D-QSAR
- Factor Xa binding affinity data reported by Quan et al. was used for the QSAR study. The affinity data[ Ki(nM)] of aryl amidino isoxazoline derivatives (Table 1-5) for factor Xa was converted to the logarithmic scale[pKi)] and then used for subsequent QSAR analyses as the response variable. All computational experiments were conducted with Cerius2 4.11[16] version QSAR environment from Accelrys (San Diego, USA) on a Silicon Graphics O2 workstation running under the IRIX 6.5 operating system. Molecular shape analysis (MSA) and Molecular field analysis (MFA) were used as the 3D-QSAR techniques. The major steps of MSA were (1) generation of conformers and energy minimization; (2) hypothesizing an active conformer (global minimum of the most active compound); (3) selecting a candidate shape reference compound (based on the active conformation); (4) performing pairwise molecular superimposition using the maximum common subgroup (MCSG) method; (5) measuring molecular shape commonality using MSA descriptors; (6) determining other molecular features by calculating quantum mechanical, spatial, electronic and conformational parameters; (7) selection of conformers; (8) generation of QSAR equations by genetic function algorithm (GFA) or stepwise regression. A complete list of descriptors used for the study molecules were presented in Table-7. Multiple conformations of each molecule were generated using the Boltzmann jump conformational search method. The upper limit of the number of conformations per molecule was 150. Each conformer was subjected to an energy minimization procedure using the smart minimizer with the Drieding force field to generate the lowest energy conformation for each structure. Varying the conformation of shape reference compound during alignment, two separate studies were conducted. In one study (MSA1) the best conformer of the most active inhibitor 51 was used as shape reference for the alignment. Best conformer was selected based on dock score and interaction energy which were obtained in flexible docking study (Ligandfit). In another study (MSA2) lowest energy conformer obtained in conformational search was used. A rigid fit of atom pairings was performed to superimpose each structure so that it overlays the shape-reference compound. The major steps of MFA were (1) generating conformers and energy minimization; (2) matching atoms using maximum common substructure (MCS) search and aligning molecules using the default options; (3) setting MFA preferences (rectangular grid with 2.00 Ao step size, charges by Gasteiger algorithm, H+, CH3 and HO- as probes); (4) creating the field; (5) analysis by the Genetic partial least squares (G/PLS) method. The MFA formalism calculates probe interaction energies on a rectangular grid around a bundle of active molecules. The surface was generated from a ‘‘Shape Field’’. The atomic coordinates of the contributing models were used to compute field values on each point of a 3D grid. Grid size was adjusted to default 2.00 A ˚. The MFA evaluates the energy between a probe (H+, CH3 and HO-) and a molecular model at a series of points defined by a rectangular grid. Fields of molecules were represented using grids in MFA and each energy associated with an MFA grid point serves as input for the calculation of a QSAR. These energies were added to the study table to form new columns headed according to the probe type. Statistical analysis of data was done using techniques like G/PLS, genetic function approximation (GFA) using QSAR+ environment of Cerius2 software. The GFA technique was used to generate a population of equations rather than one single equation for correlation between biological activity and physicochemical properties. The GFA was done as followed: (1) an initial population of equations is generated by random choice of descriptors; (2) pairs from the population of equations were chosen at random and ‘‘crossovers’’ were performed and progeny equations were generated; (3) the fitness of each progeny equation was assessed by the LOF measure; (4) a progeny equation with better fitness score was preserved. The model with a proper balance of all statistical terms explained the variance of the biological activity. The G/PLS algorithm was used as an alternative to a GFA calculation. The G/PLS is derived from two QSAR calculation methods: GFA and partial least squares (PLS). The G/PLS algorithm uses GFA to select appropriate basis functions to be used in a model of the data and PLS regression as the fitting technique to weigh the basis functions’ relative contributions in the final model.
|
|
|
|
|
2.3. Pharmacophore Modeling (Catalyst)
- All pharmacophore modeling studies were performed using Catalyst 4.11 installed on a Silicon Graphic Octane desktop Workstation. The flexibility of each molecule was represented by a set of energetically reasonable conformers which were generated with the Catalyst catConf module choosing a maximum number of 250 conformers, the best quality generation type, and an energy threshold of 20 kcal/mol beyond the calculated global energy minimum. The number of conformers generated for each molecule was limited to a maximum of 255. Ten hypotheses were generated using these conformers for each of the molecules and estimated activity values were generated after selection of the following features for the drugs; hydrogen bond donor, hydrophobic, negative charge, positive ionizable and ring aromatic. After assessing all 10 hypotheses generated for each data set, the lowest energy cost hypothesis was considered the best. The goodness of the structure activity correlation was estimated by means of the correlation coefficient (r). Catalyst also calculates the total energy cost of the generated pharmacophores from the deviation between the estimated activity and the observed activity, combined with the complexity of the hypothesis (i.e., the number of pharmacophore features). A null hypothesis was additionally calculated, which presumes that there is no relationship in the data and that experimental activities are normally distributed about their mean. Hence, the greater the difference between the energy cost of the generated hypothesis and the energy cost of the null hypothesis, the less likely it is that the hypothesis reflects a chance correlation. This criterion was then used as an assessment of the pharmacophore model selected.
3. Results & Discussion
- Results of docking studies were displayed in Table-6. Difference in interaction energy values and the binding mode of conformations (Fig-1) can be used to explain the activity variance between the molecules. Conformer with better interaction energy values for 51 (most active molecule) was isolated from the others and was used as shape reference to align all other study molecules for 3D-QSAR studies.
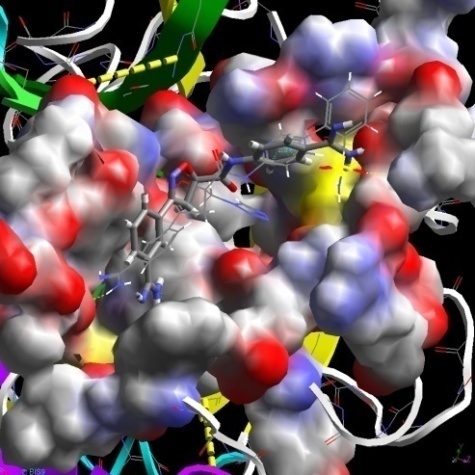 | Figure 1. Comparative view on binding modes between high (stick model) and low (cylinder model) active molecules |
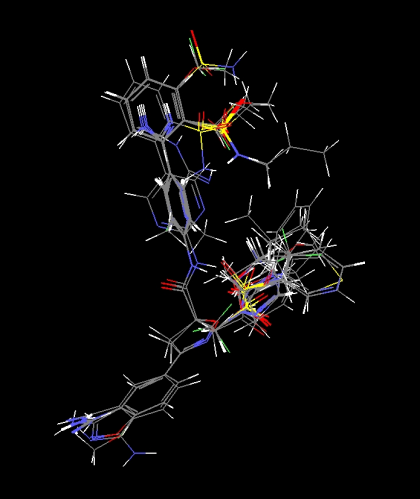 | Figure 2. Alignment of molecules for MSA1 study |
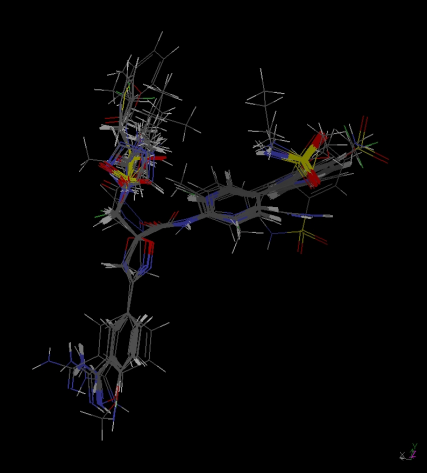 | Figure 3. Alignment of molecules for MSA2 study |
|
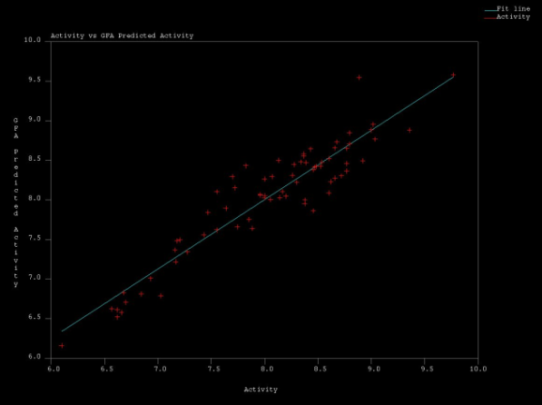 | Figure 4. Actual Vs Predicted Acitvity values obtained in MSA1 by GFA regression |
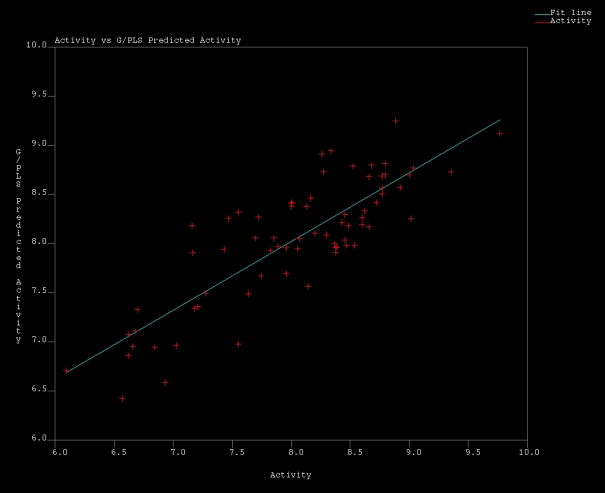 | Figure 5. Actual Vs Predicted Acitvity values obtained in MSA1 by G/PLS regression |
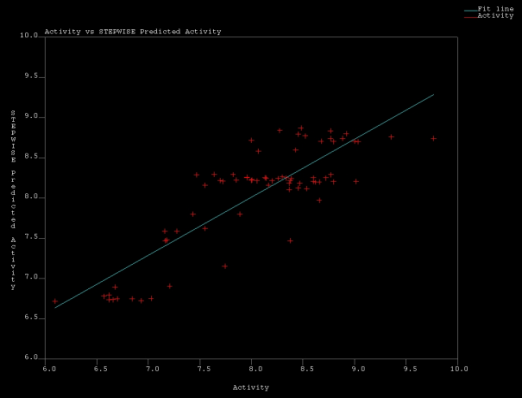 | Figure 6. Actual Vs Predicted Acitvity values obtained in MSA1 by Stepwise regression |
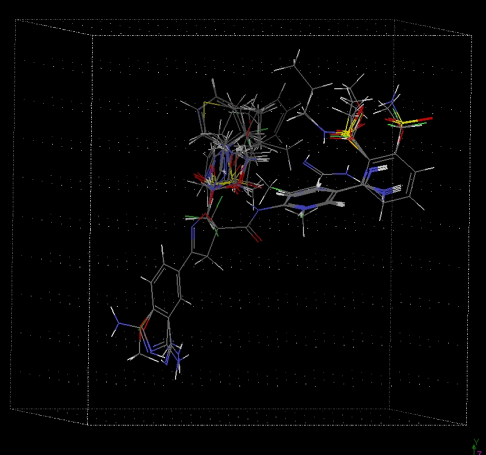 | Figure 7. Alignment of molecules for MFA study |
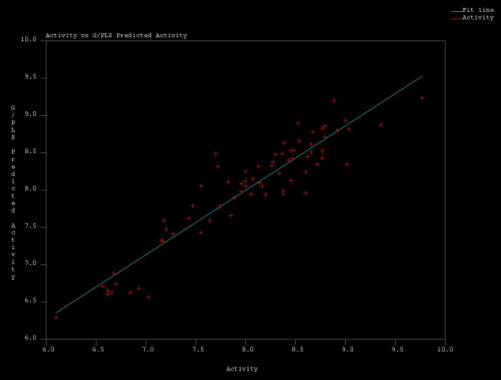 | Figure 8. Actual Vs Predicted Acitvity values obtained in MFA2 by G/PLS regression |
|
|
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
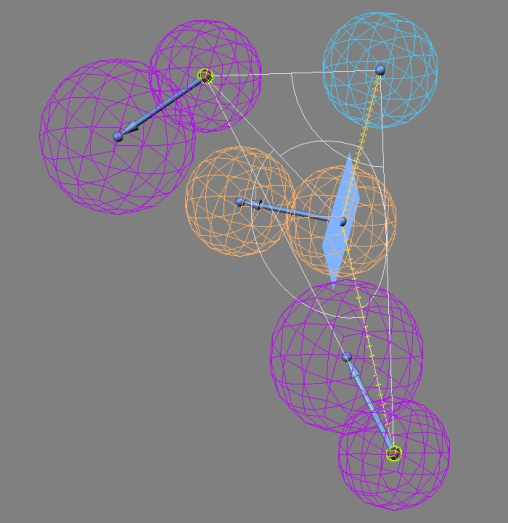 | Figure 9. Pharmacophore model showing various features required for activity. (Ra- Ring aromatic;La- Hydrophobic aromatic; Hd- Hydrogen bond donor) |
|
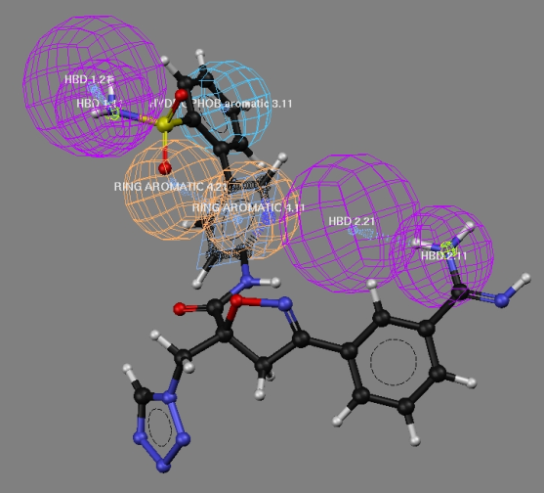 | Figure 10. Complete alignment of Pharmacophoric features observed for the most active compound of the series |
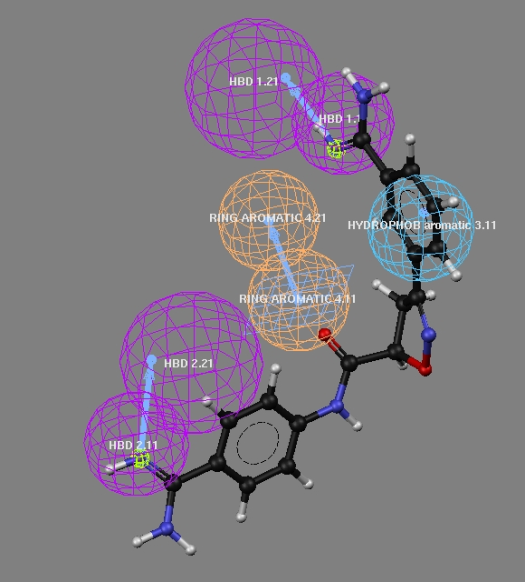 | Figure 11. Partial alignment of Pharmacophoric features observed for the low active compound of the series |
4. Conclusions
- The present 3D-QSAR analysis based on the alignment of best docked conformation explores the spatial, shape and thermodynamic requirements for the binding affinity of aryl amidino isoxazoline derivatives to factor Xa. The MSA-derived equations shows the importance of thermodynamic and quantum mechanical descriptors, molecular refractivity and radius of gyration contribution to activity. The MFA-derived equation shows interaction energies at different grid points with positive, negative and neutral bulk probes. Statistically reliable 3D-QSAR and pharmcophore models obtained from this study on aryl amidino Isoxazoline derivatives suggest that these techniques could be useful to design potent factor Xa inhibitors.
ACKNOWLEDGEMENTS
- Authors are thankful to GVK biocampus, Hyderabad, India for the facilities and technical support. The corresponding author thank the Acharya Nagarjuna University, Guntur, Andhrapradesh, India for the support of Part-time Ph.D in Pharmacy.
References
| [1] | Edgar, F.M.; Stanley, M.S.; Jocylin, A.W. Molecular modelling and drug design Pharm. & Ther. 2000, 85(3), 113–121. |
| [2] | Diane, J.M. Computational approaches to structure-based ligand design. Pharm. & Ther. 1999, 84(2), 179–191. |
| [3] | Christoph, S.; Gerhard, K. Identification and mapping of small-molecule binding sites in proteins: computational tools for structure-based drug design. Il Farmaco, 2002, 57(3), 243–251 |
| [4] | Venkatachalam, C.M.; Jiang, X.; Oldfield, T.; Waldman, M. LigandFit: A Novel Method For The Shape-Directed Rapid Docking Of Ligands To Protein Active Sites. J Mol Graph Model. 2003 21(4), 289-307. |
| [5] | Suresh, B.V.; Nilesh, R.T.; Mariam, S.D. Quantitative Structure-Activity Relationship Study of Some Aspartic Acid Analogues to Correlate and Predict their Sweetness Potency. QSAR Comb. Sci. 2007, 26,(2), 204– 214 |
| [6] | Charifson P.S. Practical applications of computer-aided drug design’ 1st ed.; Marcel Dekker Inc., New York, 1997; pp. 105–163. |
| [7] | Barnum, D.; Greene, J.; Smellie, A.; Sprague, P.Pharmacophore perception, development, and use in drug design J. Chem. Inf. Comput. Sci., 1996, 36, 563-571. |
| [8] | Schuster, D.; Maurer, E.M.;, Laggner, C.; Nashev, L.G.; Wilckens, T.; Langer T.; Odermatt, A. The discovery of new 11beta-hydroxysteroid dehydrogenase type 1 inhibitors by common feature pharmacophore modeling and virtual screening. J. Med. Chem., 2006, 49(12), 3454-66. |
| [9] | Maduskuie, T.P.; Jr, McNamara K.J.; Ru, Y.; Knabb, R.M.; Stouten, P.F. Rational design and synthesis of novel, potent bis-phenylamidine carboxylate factor Xa inhibitors. J. Med. Chem. 1998, 41(1), 53-62 |
| [10] | Matter, H.; Defossa, E.; Heinelt, U.; Blohm, P.M.; Schneider, D.; Mueller, A.; Herok, S.; Schreuder, H.A.; Liesum, A.; Brachvogel, V.; Loenze, P.; Walser, A.; Al-Obeidi, F.; Wildgoose, P. Design and quantitative structure-activity relationship of 3-amidinobenzyl-1H-indole-2-carboxamides as potent, nonchiral, and selective inhibitors of blood coagulation factor Xa.  J. Med. Chem. J. Med. Chem.  2002, 45, 2749-2769 2002, 45, 2749-2769 |
| [11] | Pancras C.W.; Mimi, L.Q.; Earl, J.; Crain, C.A.; Watson, R.W.; Robert, M.K. Nonpeptide Factor Xa Inhibitors: I. Studies with SF303 and SK549, a New Class of Potent Antithrombotics. J. Pharm. Exp. Ther. 2000, 292, 351–357. |
| [12] | Quan, M. L.; Pruitt, J.R.; Ellis, C.D.; Liauw, A.Y.; Galemmo, Jr.R.A.; Stouten, P.F.W.; Wityak, J.; Knabb, R.M.; Thoolen, M.J.; Wong, P.C.; Wexler, R.R. Nonbenzamidine isoxazoline derivatives as factor Xa inhibitors. Bio. & Med. Chem. Lett., 2003, 13, 1023–1028 |
| [13] | Quan, M.L.; Liauw, A.Y.; Ellis, C.D.; Pruitt, JR. Carini, D.J.; Bostrom, L.L.; Huang, P.P.; Harrison, K.; Knabb, R.M.; Thoolen, M.J.; Wong, P.C.; Wexler, R.R. Design and synthesis of isoxazoline derivatives as factor Xa inhibitors. 1. J. Med. Chem. 1999, 42, 2752-2759. |
| [14] | Quan, M. L.; Pruitt, J.R.; Ellis, C.D.; Liauw, A.Y.; Galemmo, Jr.R.A.; Stouten, P.F.W.; Wityak, J.; Knabb, R.M.; Thoolen, M.J.; Wong, P.C.; Wexler, R.R. Bisbenzamidine isoxazoline derivatives as factor Xa inhibitors. Bio. & Med. Chem. Lett., 1997, 7(21), 2813-2818. |
| [15] | Quan, M.L.; Liauw, A.Y.; Ellis, C.D.; Pruitt,J.R.; Carini, D.J.; Bostrom, L.L.; Huang, P.P.; Harrison, K.; Knabb, R.M.; Thoolen, M.J.; Wong, P.C.; Wexler, R.R. Design and synthesis of isoxazoline derivatives as factor Xa inhibitors. 2. J. Med. Chem. 1999, 42, 2760-2773. |
| [16] | Cerius2 Version 4.11 (2006) Accelrys Inc, San Diego, USA; http://www.accelrys.com/cerius2 |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML