-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Bioinformatics Research
p-ISSN: 2167-6992 e-ISSN: 2167-6976
2012; 2(1): 21-26
doi:10.5923/j.bioinformatics.20120201.04
Applications and Algorithms for Inference of Huge Phylogenetic Trees: a Review
Muhammad Sardaraz1, Muhammad Tahir1, Ataul Aziz Ikram1, Hassan Bajwa2
1Department of Computing and Technology, Iqra University, Islamabad, Pakistan
2Department of Electrical Engineering, University of Bridgeport, USA
Correspondence to: Muhammad Sardaraz, Department of Computing and Technology, Iqra University, Islamabad, Pakistan.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Phylogenetics enables us to use various techniques to extract evolutionary relationships from sequence analysis. Most of the phylogenetic analysis techniques produce phylogenetic trees that represent relationship between any set of species or their evolutionary history. This article presents a comprehensive survey of the applications and the algorithms for inference of huge phylogenetic trees and also gives the reader an overview of the methods currently employed for the inference of phylogenetic trees. A comprehensive comparison of the methods and algorithms is presented in this paper.
Keywords: Survey, Phylogenetic Trees, Methods for Phylogenetics
Cite this paper: Muhammad Sardaraz, Muhammad Tahir, Ataul Aziz Ikram, Hassan Bajwa, Applications and Algorithms for Inference of Huge Phylogenetic Trees: a Review, American Journal of Bioinformatics Research, Vol. 2 No. 1, 2012, pp. 21-26. doi: 10.5923/j.bioinformatics.20120201.04.
Article Outline
1. Introduction
- Phylogenetics is the study of evolutionary relationships. It enables us to use various methods to extract necessary information from a sequence. Most of the phylogenetic analysis techniques produce phylogenetic trees. These trees represent relationships between any set of species or their evolutionary history. The most accurate tree describing the evolution of a sequence can be obtained by phylogenetic analysis. Reconstruction of phylogenetic relationship using a DNA, RNA or amino acid sequences is a hierarchal process consisting of four steps[1] i.e. sequence alignment, selection of appropriate model, tree building method and the assessment of the resulting phylogeny[2].A variety of systems and applications[3-7] have been developed to infer phylogenetic trees. Early approaches were based on single node or single processor computers. Due to advances in high throughput sequencing technologies, publically available genomic data is increasing exponentially. This huge amount of data needs sophisticated, efficient and high throughput methods to be analysed. This requirement brings parallel and distributed computing to the field of bioinformatics. Recent systems and algorithms for sequence alignment and phylogenetics are based on parallel and distributed computing. This paper presents a comprehensive survey of the applications and algorithms for the inference of phylogenetic trees. Comparison of the methods and algorithms is also presented.
2. Tree Building Methods
- Different criteria are used to classify tree building methods[8]. One way is to define them as algorithm based or criteria based. Algorithm based, as the name suggests are stepwise procedures or a series of steps, while the criteria based methods follow some criteria e.g. optimization steps. Another classification is distance methods vs. character based methods. Distance method is based on the pair wise distance using some measurement, whereas in character based method trees are derived by optimizing the distribution of the patterns for each character[1,8].
2.1. Distance Methods
- Distance methods are based on pair wise distance i.e. evolutionary distance between two aligned sequences to derive a tree. To estimate the evolutionary distance an evolutionary model is applied that assumes the nature of the evolutionary changes. Pair wise distance is calculated using Maximum Likelihood (ML) estimators. The advantage of distance based method is that they are less computationally intensive than character based methods, butdisadvantage is that the actual character data is discarded. Commonly used distance based methods are Un-weighted Pair Group Method with Arithmetic mean (UPGMA)[9] and Neighbour Joining (NJ)[10]. UPGMA method selects closely related pairs of sequences to build the tree. Tree branches are joined on the basis of similarity among pairs and averages of joined pairs. When divergence relates to molecular clock it builds an accurate tree topology with true branch lengths[11,12].Neighbour joining methods use distance matrices for tree construction. It initially sums individual distances to calculate the divergence of an organism from all other organisms, and then based on this sum corrected distance matrix is evaluated. This method does not automatically yield a tree with minimum over all distance[11].
2.2. Character Based Methods
- In character based methods trees are derived by optimizing the distribution of the patterns for each character. These methods use character data in all steps of the analysis and have a little similarity among each other[41]. Character based methods include Maximum Parsimony (MP)[13] and Maximum Likelihood (ML)[14].In Maximum Parsimony method observed input sequences are explained with a minimum number of substitutions. The problem is to find a tree topology that minimizes the overall score. In many cases Parsimony methods are used as they are relatively independent of nucleotide and amino acid substitutions[1,8].Maximum Likelihood method has also been used in many systems. This method tries to find a model that has highest probability to generate the input sequence under a given evolutionary model. A likelihood of observed changes is computed and the length of the tree branch is induced by the product of likelihood. The main strength of the ML method is that we can formulate hypothesis about evolutionary relationships[1,8].Stamatakis[11] has shown that distance based methods are faster than character based methods but are less accurate. Some studies suggest that character based methods recover the true tree or topologically closer related tree to the true tree, more frequently than the distance based method[15,16].
2.3. Bayesian Inference
- This method is based on the posterior probabilities of a tree. It builds phylogenetic trees upon a likelihood function. It uses numerical methods to allow posterior probabilities to be approximated such as Markov Chain Monte Carlo (MCMC) and is presented in[17].A detail analysis of the available methods has been presented in[1,8,11,17]. Similarly overview of common distance based methods can be found in[18]. Table 1 presents comparison of different methods.
3. Survey of the Systems and Algorithms
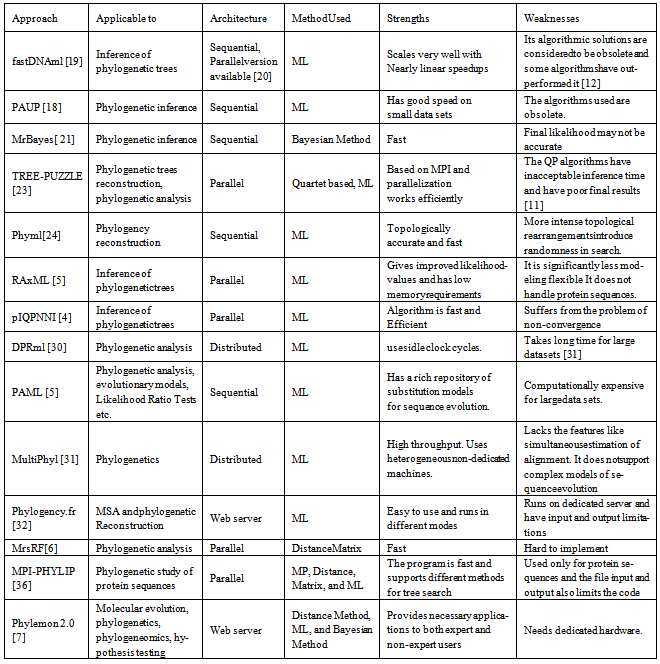
- Olson et al.[19] presented an algorithm in which a tree consisting of n taxa is built by using a stepwise addition algorithm. A local arrangement is done in order to select the best tree from each step which then gives a search space for likely trees. For n taxa a global arrangement is invoked. The algorithm scales very well with nearly linear speedups; however a study[12] has shown that its algorithmic solutions are considered to be obsolete. A parallel version of the algorithm is presented in[20].Swofford.D presented an algorithm, which is also based on stepwise addition algorithm[18]. In the algorithm local alignment is done for each taxan to find best tree and global arrangement is done to find final tree after n taxa are added.Bayesian inference method is presented in[21]. Inference of the phylogeny is based on the posterior probabilities of the phylogenetic trees. It uses Markov Chain Monte Carlo (MCMC) and also its variant Metropolis-Coupled Markov Chain Monte Carlo (MC3) analysis[22]. MCMC is used to approximate the posterior probabilities of the trees. MC3 can be visualized as a set of independent searches that occasionally exchange information, which allows a search to occasionally leap a valley that would otherwise trap it on a suboptimal hill. For both types of analysis, the final output is a set of trees that the program has repeatedly visited. A majority rule consensus tree may be built from the output trees [17].Schmidt. et al.[23] introduced quartet-puzzling (QP) algorithm. The QP algorithm consists of three steps. First it finds relationship for set of four out of n sequences. The trees are then composed into an intermediate tree adding sequences. The result of this step is highly dependent on the order of sequences[17]. As a result, many intermediate trees from different input orders are constructed. From these intermediate trees a majority rule consensus tree is built in the consensus step. The algorithm is based on MPI and parallelization works efficiently. The QP algorithms have inacceptable inference time and have poor final results[11].Guindon and Gascuel, describe an approach for phylogeny reconstruction[24]. Based on the ML method, the core of the method is an algorithm that adjusts tree topology and branch length simultaneously. Starting from an initial tree build by a fast distance based method, the algorithm modify the tree to improve the likelihood at each iteration.The algorithm is topologically accurate and fast, but introduces randomness in search due to intensive topological rearrangements.Stamatakiset al. 2005[4] present a program to infer phylogenetic trees. It uses maximum likelihood method. It is claimed that the program allows the computation of 1000 taxan trees in less than 24 hours on single processor PC. The program uses dnapars from Phylip[25] package to build initial parsimony tree. Simple evolutionary models are used to relate parsimony to maximum likelihood. Then the stepwise addition of the tree is done by dnapars. The algorithm gives improved likelihood values and memory requirements are low. It is significantly less modeling flexible and does not handle protein sequence data.Minkhet al. [3]present a modified version of the IQPNNI [26]. The IPQNNI consists of two major steps. In the initial step the local optimum likelihood tree is obtained by combining the BIONJ[27] with the Fast Nearest Neighbour Interchange[24]. In the following step leaves are randomly removed from the tree. It reinserts these leaves by important quartet puzzling (IQP) algorithm[28]. The optimization process is repeated until no further likelihood improvements are achieved. In the modified version of the algorithm the Brent’s method to determine optimal branch length is replaced by a slight modification of Newton’s method[29]. However, Newton’s method is faster as it takes the advantage of first and second order derivatives, which can be calculated efficiently. The result returned by the Newton’s method is re-evaluated to check whether re-optimization is needed. Alternatively, re-optimization may be done using Brent’s method if necessary. As the algorithm is based on the optimization step, therefore the parallelization of optimization step is done first. This algorithm is fast and efficient but suffers from the problem of non-convergence. Also sometimes the results need to be re-optimized.A study on the suitability of distributed computing for the analysis of large phylogenetic trees is presented in the work by Keane et al.[30]. A fully distributed cross platform to build phylogenetic tree is developed. It is based on maximum likelihood method and uses a popular library for phylogenetic analysis. The program is written in java and is independent of architecture and operating system. Hence it can be implemented in heterogeneous environment. The system does not need specialized hardware and is suitable for those researchers who cannot afford expensive hardware. The system can be implemented in university labs using spare clock cycles of the CPUs. The algorithm is based on hill climbing algorithm[20] with platform independence and distributed paradigm. The framework is easy to implement and does not need sophisticated hardware. A study, [31] has shown that the disadvantage of this system is that it takes excessive runtimes for large data sets.The work by Yang[5] presents a package to perform phylogenetic analysis. It uses the ML method. The package has several programs i.e. BASEML, CODEML, EVOLVER, PAMP, YN00, MCMCTREE and CH2. Primitive programs for tree search are BASEML and CODEML. The trees obtained from other programs such as Phylip[25] can also be evaluated. The package has a collection of sophisticated models used for sequence evolution. The package can perform multiple functions i.e. test of phylogenetic trees, estimation of parameters likelihood ratio test (LRTs), estimation of synonymous and non-synonymous substitutions, estimation of amino acid substitution matrices, estimation of special divergence, reconstruction of ancestral sequences and generation of nucleotide codon and amino acid sequences.Keane et al.[31] present a distributed platform for phylogenomics. It can span multiple platforms and is based on ML method. It allows the researchers to use semi-idle computers to create a virtual super computer. The platform is suitable for researchers who do not have supplicated hardware for phylogenetic analysis of large sequences. Theprogram contains three stages i.e. model selection, tree searching and bootstrapping. The program gives the user an option to select the algorithm to analyse data sets. The algorithm uses heterogeneous non-dedicated machines and has high throughput. It lacks the features like simultaneous estimation of alignment and does not support complex models of sequence evolution.Dereeperet al.[32] have developed a platform that transparently chains the programs to perform multiple sequence alignment, phylogenetic reconstruction and graphical representation of the inferred tree. This platform has been designed for both non-experienced as well as expert users. The program runs in three modes. In the non-specialist mode it provides a ready to use pipelining chain programs. It uses MUSCLE[33] for multiple sequence alignment, Gblocks[34] for automatic alignment curation andPhyml[24] for tree building. All parameters are present by default in this mode. In advance mode the pipeline is same as the one click mode but here the user can edit the setting according to his/her own requirements. In the 'A la Carte’ mode the interface remain same as in advance mode except that it offers the possibility of running and testing efficiently large methods. It runs on dedicated server and have input and output limitations for some programs.Matthewsand Williams in[6] developed an algorithm by using MapReduce[35]. This algorithm uses multi-core platform. It generates a t x t Robinson Fold (RF) matrix between t evolutionary trees. The platform uses MapReduce in a nonstandard way; typically in MapReduce framework the final out representation is smaller than initial input. But in the algorithm the output size is much larger than the input. In the first map stage hash table is generated by the MapReduce that is every bipartition is given a unique identifier. HashBase is updated by each mapper to create a local hash table.A modification of Phylip package has been done by Ropelewskiet al.[36], using MPI to enable large scale phylogenetic studies of protein sequences. It is based on increasing the number of bootstraps replication that can be performed on large scale protein data sets. This system uses Maximum Parsimony, Distance Matrix and Maximum Likelihood methods. The methodology to parallelize the Phylip program has been discussed and it performance is measured. Phylip supports heuristics and algorithms as well. The package has sampling techniques such as bootstrapping, jackknifing and permutation of characters. This package is an initial parallelization of the bootstrapped calculations on various data sets. It uses distance matrix and parsimony methods for large protein families and maximum likelihood method for moderate families. The program is fast and supports different methods for tree search. It is used only for protein sequences and the file input and output also limits the code.Tiffani. et al.[7] present a suite of web tools for molecular evolution, phylogenomics, and hypothesis testing. It integrates many applications for evolutionary analysis, format conversion, file storage, and results editing. It guides the user through the analysis for steps to follow. It provides integration of applications both to expert and non-expert users. The five major task performed by the suite are sequence alignment, phylognecy, evolutionary tests, pipeliner, and utilities. It uses Distance Method, Maximum Parsimony, Maximum Likelihood, and Bayesian Methods for tree reconstruction. The suite uses Phylip package for sequences and MrBays for Bayesian phylogeny. For Maximum Likelihood Phylip, Tree-Puzzle, and PhyML packages are used.Chen. et al.[37]present a program to construct phylogeny. Based on mixture model, the program implements a bootstrap procedure with majority rule consensus. The program uses binary sequence data to construct phylogeny. It is claimed that the program is efficient than classic methods but it is time consuming.Tamura.et al.[38] present a program for mining online databases, sequence alignment and phylogenetic trees. The program is based on ML, Distance Method and Maximum Parsimony Method. The program offers computational efficiency and accuracy of estimates for inferring.A comparison of the approaches discussed including types of architecture, method used, as well as strengths and weaknesses of each approach is given in Table 2.
|
|
4. Results and Discussion
- Performance analysis of a program for phylogenies can be done using some qualitative and quantitative parameters. The qualitative measurements include the ability of the program to handle different types of sequences i.e. DNA or amino acid sequences, as well as the ability to read sequences in different available formats etc. The quantitative measures include parameters such as the execution time of the program, final quality of the tree, and memory requirements when the size of the phylogenies is large. It is also important to know that how to be confident of the accuracy of the results obtained. Different ways may be used to analyse performance of a program. One way to analyse performance of a program is to take a set of real world data including the best known trees and a set of parameters for various programs. Another way is to take the simulated data and use different scoring functions to analyse the performance of a program[11].A study[17] has shown comparative results of different sequential programs, PAUP[18], TREE-PUZZLE[23], fastDNAml[19], and MrBays[21]. The survey is based on simulated data and results show that MrBays outperforms other analysed programs in terms of speed and quality[11]. Comparative studies have been done using multiple sets of programs with simulated and real world data[39]. It has been found that among traditional and Bayesian approaches for phylogenetic trees MrBays and Phyml are fastest and accurate approaches[11].Another study[31] has shown the comparative results of MultiPhyl[31], Phyml[24], DPRml[30], IQPNNI[26], and RaxML[4]. The results are calculated using a single processor machine and are shown in Table 3. The results show that for final likelihood values both MultiPhyl and Phyml perform similar and better than other analyzed programs. In half data sets Phyml achieves high likelihood values, whereas in the remaining half MultiPhyl achieves high final likelihood values. In the remaining programs RaxML outperforms the other analyzed programs in terms of final likelihood values. The runtime results show that on smaller data sets both Phyml and MultiPhyl comparable times but for large data sets Phyml outperforms MultiPhyl. There is also a clear difference in runtime of RaxMl and Phyml. These programs are based on faster heuristics and have better performance as compared to traditional Maximum Likelihood programs. It is still time consuming task to perform phylogenetic analysis of large scale data on a single processor. One solution of this problem is to use parallel processing to perform high throughput phylogenetic analysis. This solution is however expensive as dedicated hardware is required. This can be avoided if non-dedicated heterogeneous processors are used [31]. Parallel and distributed computing addresses the problem of computational complexity and speeds up the algorithms for phylogenies.
5. Conclusions
- Phylogenetic analysis tells us about the relationship among different organisms and their evolutionary history. The analysis of publically available genomic data needs efficient and high throughput programs. This article explored various methods for phylogenetics and various approaches for inference of huge phylogenetic trees along with the methods and approaches used. As the genomic data is increasing exponentially; the developed approach must be computationally less intensive and must have low memory requirements. These goals can be achieved by constructing good heuristics that run on parallel systems with low memory requirements.
References
| [1] | M. Talianova, 2007, Survey of molecular phylogenetics: A review, Plant Soil Environ ,53(9), 413–416 |
| [2] | M. Steel, 2005, Should phylogenetic models be trying to “fit an elephant”?, Trends Genet, 21(6), 307–309 |
| [3] | BQ. Minh, LS..Vinh, A. Haeseler, and HA. Schmidt, 2005,pIQPNNI: parallel reconstruction of large maximum likelihood phylogenies., Bioinformatics ,21(19), 3794–3796 |
| [4] | A. Stamatakis, T. Ludwig, and H. Meier, 2005,RAxML-III: a fast program for maximum likelihood-based inference of large phylogenetic trees, Bioinformatics , 21(4), 456–463 |
| [5] | Z. Yang, 2007, PAML 4: phylogenetic analysis by maximum likelihood, Mol. Biol. Evol 24(8), 1586–1591 |
| [6] | Matthews SJ, and Williams TL, 2010, MrsRF: an efficient MapReduce algorithm for analyzing large collections of evolutionary trees, Bioinformatics11 (Suppl): S15doi: 10.1186/ 1471-2105-11-S1-S15. |
| [7] | Sanchez. R, Serra. F, Tarraga. J, Medina. I, Carbonell. J, Pulido.L, Maria. A, Capella-Gutierrez. S, Huerta-Cepas. J, Gabaldon. T, Dopazo. J, and Dopazo .H ,2011,Phylemon 2.0: a suite of web-tools for molecular evolution, phylogenetics, phylogenomics and hypotheses testing, Nucleic Acids Research 39: doi: 10.1093/nar/gkr408 |
| [8] | Baxevanis. AD and Ouellette. BFF, Bioinformatics: A Practical Guide to the Analysis of Genes and Proteins. John Wiley & Sons, Inc. Hoboken, New Jersey,1998 |
| [9] | Sokal. RR, Michener. CD ,1958, A statistical method for evaluating systematic relationships, Sci. Bull, 38, 1409–1438 |
| [10] | Saitou. N and Nei. M, 1987, The Neighbor-Joining method: A new method for reconstructing phylogenetic trees, Mol. Biol. Evol 4(4), 406–425. |
| [11] | Stamatakis. A, “Distributed and Parallel Algorithms and Systems for Inference of Huge Phylogenetic Trees Based on the Maximum Likelihood Method” PhD thesis, TechnischeUniversitat, Munchen, Germany, 2004 |
| [12] | Trystram. D and Zola. J, Grid Computing for Bioinformatis and Computational Biology, John Wiley & Sons, Inc., Hoboken, New Jersey, 2008 |
| [13] | Edwards.A,and Cavalli-Sforza. LL, 1963, The reconstruction of evolution, Heredity, 18, 553 |
| [14] | Cavalli-Sforza LL, and Edwards. A 1967, Phylogenetic analysis: Models and estimation procedures, Hum. Genet 19(3), 233–257 |
| [15] | Huelsenbeck. J, Hillis. D, 1993, Success of phylogenetic methods in the four-taxon case, Syst. Biol, 42(3), 247–264 |
| [16] | Huelsenbeck. J, 1995, Performance of phylogenetic methods in simulation, Syst. Biol 44(1), 17–48 |
| [17] | Tiffani.L,and Bernard. M,2003, An Investigation of Phylogenetic Likelihood Methods, Proc. BIBE03,79-86 |
| [18] | Swofford. D, PAUP∗:Phylogenetic analysis using parsimony (and other methods), Sinauer Associates, Sunderland, MA, 1996 |
| [19] | Olson. G, Matsuda. H, Hagstrom. R andOverbeek. R, 1994,fastDNAml: A tool for construction of phylogenetic trees of dna sequences using maximum likelihood, ComputApplBiosci 10(1), 41–48. |
| [20] | Stewart. CA. Hart. D, Berry. DK., Olsen. GJ, Wernert. EA and Fischer. W, 2001, Parallel implementation and performance of fastDNAml a program for maximum likelihood phylogenetic inference, Procs of SC, 32 |
| [21] | Huelsenbeck. J andRonquist. F 2001, MrBayes:Bayesian inference of phylogenetic trees, Bioinformatics 17(8), 754–755. |
| [22] | Geyer. J 1991, Markov chain Monte Carlo maximum likelihood, Proc of the 23rd Symposium on the Interface, 156–163. |
| [23] | Schmidt. HA, Strimmer. K, Vingron. M and Haeseler. A, 2002, Tree-puzzle: maximum likelihood phylogenetic analysis using quartets and parallel computing, Bioinformatics 18(3), 502–504. |
| [24] | Guindon.S,andGascuel. O. 2003,A simple, fast, and accurate algorithm to estimate large phylogenies by maximum likelihood, Syst. Biol 52(5), 696–704. |
| [25] | Felsenstein. J, 1989, PHYLIP - Phylogeny Inference Package (Version 3.2), Cladistics 5, 164–166. |
| [26] | Vinh. LS and Haeseler. A, 2004, IQPNNI: Moving fast through tree space and stopping in time, Mol. Biol. Evol, 21(8), 1565–1571. |
| [27] | Gascuel. O, 1997, BIONJ: An improved version of the NJ algorithm based on a simple model of sequence data, Mol. Biol. Evol, 14(7), 685–695. |
| [28] | Strimmer. K and Haeseler. A,1996, Quartet puzzling: A quartet maximum likelihood method for reconstructing tree topologies, Mol. Biol. Evol, 13(7), 964–969. |
| [29] | Press. WH, Teukolsky. SA, Vetterling. WT and Flannery. BP, Numerical Recipes in C: The Art of Scientific Computing, Cambridge University Press, Cambridge, 1992. |
| [30] | Keane. TM,Naughton. TJ, Travers. SA, McInerney. JOand McCormack. GP, 2005,DPRml: Distributed Phylogeny Reconstruction by Maximum Likelihood, Bioinformatics 21(7), 969-974. |
| [31] | Keane. TM,Naughton. TJ andMcInerney. JO, 2007,MultiPhyl: a high-throughput phylogenomics webserver using distributed computting, Nucleic Acids Research, 35(2), 33–37. |
| [32] | Dereeper. A, Guignon. V, Blanc. G, Audic. S, Buffet. S, Chevenet. F, Dufayard. JF, Guindon. S, Lefort. V, Lescot. M, Claverie. JM andGascuel. O, 2007, Phylogeny.fr: robust phylogenetic analysis for the non-specialist, Nucleic Acids Research, 36, 465–469. |
| [33] | Edgar. RC, 2004, MUSCLE: a multiple sequence alignment method with reduced time and space complexity, BMC Bioinformatics, 5, 113. |
| [34] | Castresana. J,2000, Selection of conserved blocks for multiple alignments for their use in phylogenetic alignments, Mol. Biol.Evol,17(4), 540–552. |
| [35] | Dean.J,andGhemawat. S, 2008,MapReduce: Simplified Data Processing on Large Clusters, Proc. OSDI, 137–150 |
| [36] | Ropelewski. AJ, Nicholas.HB, and Mendez. RR, 2010,MPI-PHYLIP: Parallelizing Computationally Intensive Phylogenetic Analysis Routines for the Analysis of Large Protein Families., PLoS ONE 5(11): e13999. doi:10.1371/journal.pone.0013999. |
| [37] | Chen. SC, Rosenberg. MSand Lindsay. BG., 2011, MixtureTree: a program for constructing phylogeny,BMC Bioinformatics 12: :111doi:10.1186/1471-2105-12-111 |
| [38] | Tamura. K, Peterson. D, Peterson. N, Stecher. G, Nei. M and Kumar .S, 2011, MEGA5: Molecular Evolutionary Genetics Analysis Using Maximum Likelihood, Evolutionary Distance, and Maximum Parsimony Methods, Mol. Biol. Evoldoi: 10.1093/molbev/msr121. |
| [39] | Stamatakis. A, Ludwig.T,and Meier. H, 2004, New Fast and Accurate Heuristics for Inference of Large Phylogenetic trees. Proc. IPDPS, 26-30. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML