-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Astronomy
p-ISSN: 2169-8848 e-ISSN: 2169-8856
2024; 13(1): 1-3
doi:10.5923/j.astronomy.20241301.01
Received: Mar. 2, 2024; Accepted: Mar. 21, 2024; Published: Mar. 22, 2024

Accelerating Universe and Cosmological Equivalence
Ranku Kalita
Independent Researcher, Guwahati, Assam, India
Correspondence to: Ranku Kalita , Independent Researcher, Guwahati, Assam, India.
| Email: |  |
Copyright © 2024 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The expansion of the universe is presently accelerating. Since the universe was earlier expanding gravitationally deceleratingly, and was therefore a dynamically viable universe, the question then arises as to why is the universe now expanding acceleratingly at all? The principle of equivalence recognizes the indistinguishability between gravitational freefall of a gravitational mass, and the impressional freefall of a stationary inertial mass with respect to an observer in an accelerating frame of reference. In other words, the gravitational effect of matter, in terms of freefall of gravitational mass, is equivalent to the inertial effect of motion, in terms of freefall of inertial mass. Thus, along with gravitational mass coexisting in magnitudinal equivalence with inertial mass, matter and its gravitational-freefall effect upon gravitational mass coexists in phenomenal equivalence with motion and its inertial-freefall effect upon inertial mass of objects. Gravitational mass of objects was in cosmological freefall when the universe was earlier expanding deceleratingly. The cosmological constant, which parametrizes the presently accelerating expansion of the universe, may be seen to be also acting upon inertial mass of objects in the universe, thereby rendering it in cosmological freefall. The accelerating expansion of the universe, therefore, manifests cosmological equivalence between the effect of motion, in terms of cosmological freefall of inertial mass, and the effect of matter, in terms of cosmological freefall of gravitational mass of objects.
Keywords: Accelerating universe, Cosmological constant, Dark energy
Cite this paper: Ranku Kalita , Accelerating Universe and Cosmological Equivalence, International Journal of Astronomy, Vol. 13 No. 1, 2024, pp. 1-3. doi: 10.5923/j.astronomy.20241301.01.
1. Introduction
- The presently observed accelerating expansion of the universe has come as a surprise, contrary to the expectation of a gravitationally decelerating expansion, which has been the dynamics of the universe since the big bang, before it started to expand acceleratingly ~ 6×109 years ago [1]. It is possible to have a dynamically viable universe that was earlier expanding gravitationally deceleratingly – it is not necessary for the universe to have to expand acceleratingly for it to exist. The question therefore arises, as to why is the universe expanding acceleratingly now? The accelerating expansion of the universe is parametrized by the cosmological constant. Attention has therefore been focused on the existence and origin of the cosmological constant. The cosmological constant was originally introduced by Einstein in the field equations of general relativity, to balance gravitation so as to account for what was then believed to be a static universe [2]. However, the instability of a static universe model due to matter density perturbations, and subsequent observational evidence in the 1920s of an expanding universe [3] rendered the cosmological constant redundant. Observations in the 1990s that the expansion of the universe is accelerating [1,4], however, has required the resurrection of the cosmological constant.The field equation containing the gravitational term and cosmological-constant term is
 | (1) |
 ; the negative spacetime curvature gravitational term is
; the negative spacetime curvature gravitational term is 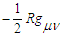 , the curvature of which is determined by energy-momentum tensor
, the curvature of which is determined by energy-momentum tensor  of matter and radiation on the right-hand side of equation (1); the positive cosmological-constant term is
of matter and radiation on the right-hand side of equation (1); the positive cosmological-constant term is  and the cosmological constant
and the cosmological constant  determines the constancy of spacetime curvature
determines the constancy of spacetime curvature  .It is possible to formulate the cosmological constant as an energy density term
.It is possible to formulate the cosmological constant as an energy density term  . By crossing over from classical field theory of general relativity to quantum field theory of particle physics, the energy density of the cosmological constant may be sourced from the vacuum, representing zero-point energy, i.e., the lowest energy state of the particles in the universe. A naïve calculation, however, yields the infamous 120 orders of magnitude discrepancy between the predicted and observed value of the vacuum energy density [5].Be that as it may, aside from seeking the quantum vacuum origin of the cosmological constant to explain its existence, since the cosmological constant is a part of classical general relativity, we may also seek to understand its existence in terms of its role in the dynamics of the universe. However, since dynamically it is possible to have a viable universe that was earlier expanding gravitationally deceleratingly, therefore the presently accelerating expansion of the universe seems superfluous. Is there then a deeper physical significance to the accelerating expansion of the universe?The principle of equivalence recognizes that gravitational freefall of gravitational mass of an object is indistinguishable from impressional freefall of inertial mass of a stationary object with respect to an observer in an accelerating frame of reference. To put it in another way, the gravitational effect of matter, in causing gravitational-mass freefall, is indistinguishable from the inertial effect of motion, in causing inertial-mass freefall.1 Thus, along with gravitational mass coexisting magnitudinally equivalently with inertial mass in objects, matter and its gravitational-freefall effect upon gravitational mass coexists phenomenally equivalently with motion and its inertial-freefall effect upon inertial mass of objects. While technically it is true that impressional freefall of inertial mass is equivalent to physical freefall of gravitational mass, from the physical point of view there should be scope for physical freefall of inertial mass as well. And indeed, the cosmological constant, which accelerates the expansion of the universe, can be seen to also play the role of causing physical cosmological freefall of inertial mass – and thereby manifesting cosmological equivalence with physical cosmological freefall of gravitational mass of objects.
. By crossing over from classical field theory of general relativity to quantum field theory of particle physics, the energy density of the cosmological constant may be sourced from the vacuum, representing zero-point energy, i.e., the lowest energy state of the particles in the universe. A naïve calculation, however, yields the infamous 120 orders of magnitude discrepancy between the predicted and observed value of the vacuum energy density [5].Be that as it may, aside from seeking the quantum vacuum origin of the cosmological constant to explain its existence, since the cosmological constant is a part of classical general relativity, we may also seek to understand its existence in terms of its role in the dynamics of the universe. However, since dynamically it is possible to have a viable universe that was earlier expanding gravitationally deceleratingly, therefore the presently accelerating expansion of the universe seems superfluous. Is there then a deeper physical significance to the accelerating expansion of the universe?The principle of equivalence recognizes that gravitational freefall of gravitational mass of an object is indistinguishable from impressional freefall of inertial mass of a stationary object with respect to an observer in an accelerating frame of reference. To put it in another way, the gravitational effect of matter, in causing gravitational-mass freefall, is indistinguishable from the inertial effect of motion, in causing inertial-mass freefall.1 Thus, along with gravitational mass coexisting magnitudinally equivalently with inertial mass in objects, matter and its gravitational-freefall effect upon gravitational mass coexists phenomenally equivalently with motion and its inertial-freefall effect upon inertial mass of objects. While technically it is true that impressional freefall of inertial mass is equivalent to physical freefall of gravitational mass, from the physical point of view there should be scope for physical freefall of inertial mass as well. And indeed, the cosmological constant, which accelerates the expansion of the universe, can be seen to also play the role of causing physical cosmological freefall of inertial mass – and thereby manifesting cosmological equivalence with physical cosmological freefall of gravitational mass of objects. 2. Cosmological Equivalence
- The description of earlier gravitationally decelerating expansion, and presently accelerating expansion of the universe due to the cosmological constant, is in the second Friedmann equation:
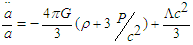 | (2) |
 along with matter density
along with matter density  is responsible for the earlier gravitationally decelerating expansion, while the positive term with the cosmological constant
is responsible for the earlier gravitationally decelerating expansion, while the positive term with the cosmological constant  is responsible for the presently accelerating expansion of the universe.Now, if we want to connect the dynamics of the universe with its discrete material constituents, we need to have a Newtonian formulation, which involves the description of gravitational deceleration acting upon gravitational mass of an object, whereby it would be in cosmological gravitational freefall in the earlier gravitationally decelerating expanding universe; we therefore re-cast equation (2) as an equation of motion of mass
is responsible for the presently accelerating expansion of the universe.Now, if we want to connect the dynamics of the universe with its discrete material constituents, we need to have a Newtonian formulation, which involves the description of gravitational deceleration acting upon gravitational mass of an object, whereby it would be in cosmological gravitational freefall in the earlier gravitationally decelerating expanding universe; we therefore re-cast equation (2) as an equation of motion of mass  on the surface of an expanding spherical distribution of matter
on the surface of an expanding spherical distribution of matter 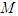 , with radius
, with radius  , and pressure
, and pressure  ; since
; since 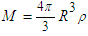 , we have [6]:
, we have [6]:  | (3) |
 in equation (3), it is evident how the gravitational term
in equation (3), it is evident how the gravitational term 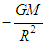 and cosmological constant term
and cosmological constant term 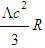 act upon it:
act upon it: | (4) |
 is the gravitational term, we may infer that it is acting upon gravitational mass
is the gravitational term, we may infer that it is acting upon gravitational mass  of
of 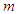 ; and since gravitational mass is magnitudinally equivalent to inertial mass, we may then infer that the cosmological-constant term
; and since gravitational mass is magnitudinally equivalent to inertial mass, we may then infer that the cosmological-constant term  is acting upon inertial mass
is acting upon inertial mass 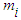 of
of  :
: | (5) |
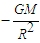 , is independent of the magnitude of
, is independent of the magnitude of  , and only depends upon distance
, and only depends upon distance 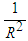 , whereby
, whereby 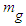 is in freefall; similarly, inertial-mass acceleration, determined by the cosmological-constant term
is in freefall; similarly, inertial-mass acceleration, determined by the cosmological-constant term 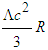 , is independent of the magnitude of
, is independent of the magnitude of 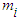 , and only depends upon distance
, and only depends upon distance 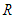 , whereby
, whereby 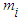 is in freefall. Since both gravitational and inertial mass of objects are in freefall, there is therefore cosmological phenomenal equivalence between them; however, since gravitational-mass cosmological freefall decelerates as
is in freefall. Since both gravitational and inertial mass of objects are in freefall, there is therefore cosmological phenomenal equivalence between them; however, since gravitational-mass cosmological freefall decelerates as 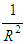 , while inertial-mass cosmological freefall accelerates as
, while inertial-mass cosmological freefall accelerates as 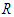 , there is therefore no magnitudinal equivalence, except momentarily, when in an expanding
, there is therefore no magnitudinal equivalence, except momentarily, when in an expanding 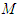 , at a certain radial distance
, at a certain radial distance 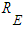 , deceleration and acceleration are balanced.With
, deceleration and acceleration are balanced.With  in equation (3), we can then derive radius
in equation (3), we can then derive radius 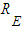 :
:  | (6) |
 is expanding deceleratingly, and when
is expanding deceleratingly, and when 
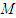 is expanding acceleratingly. Since both gravitational term
is expanding acceleratingly. Since both gravitational term 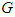 and cosmological-constant term
and cosmological-constant term 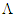 are present as numerator and denominator in equation (6), however, neither is expansion of
are present as numerator and denominator in equation (6), however, neither is expansion of  purely decelerating when
purely decelerating when  nor purely accelerating when
nor purely accelerating when  , but is a blend of both, with the former or the latter being the dominant dynamic, when
, but is a blend of both, with the former or the latter being the dominant dynamic, when 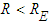 or
or 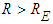 . In terms of mass
. In terms of mass 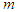 ,
, 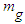 of
of  would be the ‘dominant participant’ in decelerating freefall of
would be the ‘dominant participant’ in decelerating freefall of 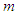 when
when 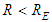 , while
, while 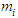 of
of 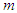 is the ‘dominant participant’ in accelerating freefall of
is the ‘dominant participant’ in accelerating freefall of 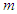 when
when 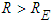 .
.3. Discussion
- Our familiar notion of equivalence between gravitational-mass freefall and inertial-mass freefall is about how impressional inertial-mass freefall mimics physical gravitational-mass freefall. This, however, implies a bias in favour of gravitational-mass freefall as being the standard manifestation of freefall. Rather, if gravitational and inertial-mass freefall are to be truly equivalent, it should be mainly about how the fundamental phenomenon of freefall can be manifested by both gravitational and inertial mass – irrespective of the direction and magnitude of acceleration of inertial-mass freefall compared to gravitational-mass freefall. Indeed, this is powerfully manifested by cosmological equivalence between gravitational and inertial-mass freefall, wherein the positive cosmological-constant acceleration which causes inertial-mass cosmological freefall is in the opposite direction to negative gravitational acceleration, which causes gravitational-mass cosmological freefall; and the acceleration/deceleration are also necessarily magnitudinally dissimilar, for the universe to be able to manifest the dual dynamics of earlier gravitationally decelerating and presently antigravitationally accelerating expansion; further, unlike local freefall of inertial mass, which is impressional, while freefall of gravitational mass is physical, cosmological freefall of inertial mass, due to it being accelerated by the cosmological constant, is physical, just like cosmological physical freefall of gravitational mass.
4. Conclusions
- The presently accelerating expansion of the universe succeeded the earlier gravitationally decelerating expansion. Since it is possible to have a dynamically viable universe that was expanding gravitationally deceleratingly, the necessity of accelerating expansion seems unclear. The principle of equivalence recognizes the indistinguishability between gravitational freefall of gravitational mass and impressional freefall of a stationary inertial mass, with respect to an observer in an accelerating frame of reference. Another way of stating it would be that the gravitational effect of matter, rendering freefall of gravitational mass, is equivalent to inertial effect of motion, rendering freefall of inertial mass of an object. Thus, along with gravitational mass coexisting in magnitudinal equivalence with inertial mass, matter and its gravitational-freefall effect upon gravitational mass coexists in phenomenal equivalence with motion and its inertial-freefall effect upon inertial mass of objects. Previously, in the gravitationally decelerating expanding universe, gravitational mass of objects was in gravitational cosmological freefall. The presently accelerating expansion of the universe is parametrized by the cosmological constant. The cosmological constant may be seen to also act upon the inertial mass of objects in the universe, whereby it is in anti-gravitational cosmological freefall. The accelerating expansion of the universe is therefore manifesting cosmological equivalence between cosmological freefall of inertial mass and gravitational mass of objects.
Notes
- 1. The statement that 'gravitational effect of matter in causing gravitational-mass freefall is indistinguishable from the inertial effect of motion in causing inertial mass-freefall' reduces to the fact that both gravitational and inertial mass are in a locally inertial frame of reference, within the accelerating frame of reference of freefall, and therefore we may say that the effect of motion in the form of an accelerating frame of reference of freefall is (locally) inertial for inertial mass, just as the effect of matter in the form of a gravitational accelerating frame of reference of freefall is also (locally) inertial for gravitational mass.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML