Adrián G. Cornejo
Electronics and Communications Engineering from Universidad Iberoamericana, Santa Rosa, Querétaro, Mexico
Correspondence to: Adrián G. Cornejo, Electronics and Communications Engineering from Universidad Iberoamericana, Santa Rosa, Querétaro, Mexico.
| Email: |  |
Copyright © 2023 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
In this work, we explore a noncompactified model of a charged point particle of five-dimensional size in an external magnetic field. This model follows the idea of a fifth dimension as an extremely very small length scale (from our usual point of view of dimensional scale) in a very small region of space-time. To define the size of such a 5D scale, we recalculate the length of a test charged point particle in the five-dimension related to the electron (first proposed by Klein) from the electrogravitational coupling constant, estimating the radius to be approximately 7.4×1018 smaller than the radius of the electron. Considering an external magnetic field, the angular momentum of the charged point particle of five-dimensional size can be estimated. Extending the same analysis to some other fermions, the characteristic values of their respective point particle of 5D-size are calculated.
Keywords:
Kaluza-Klein theory, Jordan-Thiry theory, Electrogravitational coupling constant
Cite this paper: Adrián G. Cornejo, Model of a Point Particle of 5D-size in an External Magnetic Field, International Journal of Astronomy, Vol. 12 No. 1, 2023, pp. 15-20. doi: 10.5923/j.astronomy.20231201.03.
1. Introduction
In his attempt at a theory of unification that included both four-dimensional theories, electromagnetism and gravity, Kaluza obtained a 5×5 matrix [1], proposing a subspace of a five-dimensional Riemannian space. He also introduced the restriction of the “cylinder condition” for the subspace relative to the fifth coordinate, that no component of the five-dimensional metric depends on the fifth dimension. This condition would form a compacted reference frame. Following Kaluza’s idea, Klein combined it with some ideas from quantum mechanics [2,3] and was able to propose a first quantitative estimate of both the quantization of the charge and the smallness of the particle in the fifth dimension, calculating a length to be approx. 0.8×10-30 cm for a five-dimensional point particle related to the electron. The works of Kaluza and Klein realized that the form for the electromagnetic stress-energy tensor emerges from the 5D vacuum equations as a source in the 4D equations. Furthermore, Klein proposed that a point particle in the fifth spatial dimension would be rotating in a circle with a very small radius, so that such a particle would move a short distance along a rotation axis. Thus, the 5D particle in motion should return to the position from which it began. The distance that the point particle must travel before reaching its initial position was considered to be a representation of the size of the extra fifth dimension. This extra dimension was then considered similar to a “compact” set for a fourth-dimensional point of view. However, Kaluza and Klein had assumed the scalar field as constant. In this way, the Klein model for the length of a particle in five dimensions resulted in a value that did not seem to make sense when compared with the physical rest mass of the electron [4], besides that Klein’s formula did not satisfy the dimensional units for momentum, which can be easily verified [5] as follows: Considering the Klein equation [3], written as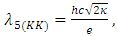 | (1) |
where κ is the gravitational constant used by Einstein, h is Planck’s constant, λ5(KK) is the length in the Kaluza-Klein model, e is the electron charge (written as positive), and c is the speed of light. According to the de Broglie equation, momentum is given as p = h/λ. Solving Eq. (1) for momentum, we get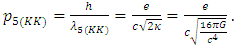 | (2) |
Substituting respective values in SI units, yields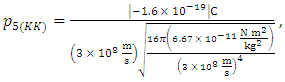 | (3) |
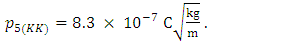 | (4) |
It is verified that Eq. (2) does not satisfy the corresponding units of momentum [6]. The same result can also be confirmed in CGS units. In modern geometry, the extra fifth dimension can be understood to be the circle group, corresponding to a U(1) by a general Lie group, as electromagnetism can essentially be formulated as a gauge theory on a fiber bundle, the circle bundle, with gauge group U(1). This group suggests that gauge symmetry is the circular symmetry, and Kaluza-Klein theory treats the more general case of curved space-time. By considering a principal fiber bundle P with gauge group G over a manifold M = M4×S1. Given a connection on the bundle, and a metric on the base manifold, and a gauge invariant metric on the tangent of each fiber, it is possible to construct a bundle metric defined on the entire bundle [7]. Kaluza-Klein geometry is related to an invariant metric on the circle S1 that is the fiber of the U(1)-bundle of electromagnetism. The invariance of the metric is such that it is invariant to rotations of the circle. Furthermore, in the 1940s, three main independent research groups obtained the complete field equations [8-10], which allowed the scalar field to vary properly. This analysis is also known as the Jordan-Thiry theory [11] and was developed in the geometric framework of a five-dimensional Riemannian manifold. It was based on eliminating the condition that the vector field related to the geometric structure of the space considered by Kaluza as constant, and they related the scalar field to the gravitational constant. Thus, the condition of the variable γ55 is a coupling “constant”, originally called β, for the gravitational interaction that is a function of the coordinates, which is the characteristic parameter of the electrogravitational scale of Kaluza’s theory. It combines the Newtonian constant of gravitation and the permeability of free space μ0 (or the permittivity of free space ε0) [12], given as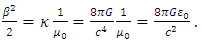 | (5) |
From the Lagrangian density of electromagnetism in general relativity, the equation with the coupling constant can be written in the form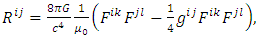 | (6) |
where F is the electromagnetic tensor. In the considered metric of the gravity in five dimensions, the indices were allowed by Kaluza to range over 0, 1, 2, 3, 4 with (−, +, +, +, +) signature. Following the Kaluza metric, we use in this work a modified metric with (+, +, +, +, −) signature by adopting the notation of 5 (instead of 0) for the fifth dimension, giving the line-element (square) in Cartesian coordinates as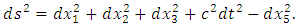 | (7) |
Here, Greek indices range from 1 to 5, the subscript and superscript 5 indicates the fifth dimension. On the other hand, there is an extensive literature on defined theories in extra dimensions (even textbooks). However, most of them treat the particles in extra dimensions as strings, extending into toroidal topology, in compact dimensions, and even following the original analysis with the constant scalar field as considered by Kaluza and Klein, among others. In addition, when the time came to include the strong and weak forces by extending Kaluza mechanism to higher dimensions, it was assumed a priori that these too would be compact. These treatments, mainly from mathematical considerations, contain their own model with a particular physical interpretation of the particles in extra dimensions, respectively. Therefore, following any of these models as a dogma to develop other extra dimensional theories, in particular, for particles of five-dimensional size, could limit some new or different physical interpretation to study and analyze such type of quantum particles, and their possible qualities in the space-time. Theoretical challenges in standard cosmology and quantum mechanics, such as the problem of the quantum particles in extra dimensions motivate the development and search of different models that consider additional parameters, as well as new alternatives and possibilities. Motivated by this interest, we explore a noncompactified model of a charged point particle of five-dimensional size in an external magnetic field. This model follows the idea of a fifth dimension as an extremely very small length scale (from our usual point of view of dimensional scale) in a very small region of space-time. The physical interpretation of a particle of five-dimensional size that we explore in this model is that of a specific charged point particle with spherical topology and an extremely very small size, which should have a specific size, rest mass and charge, occupying a very small noncompactified region in the space-time, and interacting with an external magnetic field to cover a space (either area or volume) during its vibration in the magnetic field [13,14]. Thus, in a noncompactified approach, there is no reason to compactify the fifth dimension, i.e., a “cylinder condition” is not required. Although we are modeling with charged point particles that rotate in an external electromagnetic field, we find a similarity in the results with a type of basic particles defined in String theory, specifically for a closed string, mainly in the aspect that the trajectory that these point particles trace when they rotate in the electromagnetic field resembles that of a string. Even, we derive an analogous equation with the same characteristics of a basic closed string. However, we consider that a closed string could only be possible in a static universe, since due to the propagation of time (in an expanding universe), any particle would not return to the same place in space-time from which it began. In this context, only the existence of open strings in the dynamics of space-time can be possible (see Figure 2). Considering the coupling constant, in Section 2 we recalculate the length and charge of a test charged point particle of five-dimensional size related to the electron (first proposed by Klein). In Section 3, the rest mass for that a point particle of 5D-size is calculated. In Section 4, we extrapolate the charged point particles in an electromagnetic field analysis from 4D to those of 5D-size. In Section 5, extending this analysis, we estimate the characteristic values of some other charged point particles of fifth-dimensional size.
2. The Length of a Test Charged Point Particle of Five-Dimensional Size
We will begin this analysis by recalculating the length of the radius of a test charged point particle of five-dimensional size related to the electron, now considering the coupling constant. Following the same Klein’s consideration that relates the de Broglie equation for the momentum of a point particle in five-dimensions, given as 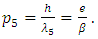 | (8) |
Considering the coupling constant from Eq. (5), the length in the five-dimensional size can be written as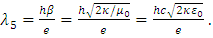 | (9) |
Thus, Eqs. (8) and (9) are the updated Klein’s Ansatz. Solving Eq. (8) for the momentum p5 in SI units, yields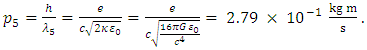 | (10) |
This expression correctly satisfies the units for momentum.Substituting the permittivity of free space (namely, 8.85×10-12 F·m-1), the length is recalculated as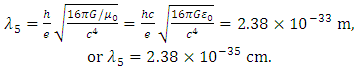 | (11) |
Considering that length λ = 2πR, the related radius R5 can be derived from Eq. (9) as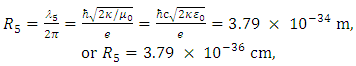 | (12) |
where ħ is the reduced Planck’s constant. This is a significant result for the smallness of a point particle of 5D-size. In this sense, when a moving test charged point particle of 5D-size reaches the electron charge, from Eq. (12) is obtained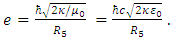 | (13) |
The ratio between both radii Re and radius R5 can be calculated as 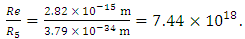 | (14) |
Furthermore, considering the de Broglie equation for the momentum of the electron given by a test charged point particle (q5) of five-dimensional size, yields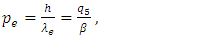 | (15) |
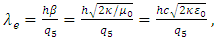 | (16) |
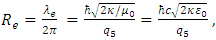 | (17) |
where solving for the charged point particle q5 and substituting the respective values in SI units, gives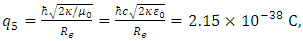 | (18) |
which is an expression analogous to Eq. (13). The ratio between electron charge and the estimated charge of the point particle of five-dimensional size remains the same value, given as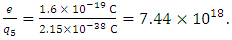 | (19) |
3. The Rest Mass of a Charged Point Particle of Five-Dimensional Size from the Coupling Constant
Considering a test charged point particle of radius R5 and charge q5 of a five-dimensional size, the corresponding rest mass m5 can be calculated by considering the Biot-Savart law and the Lorentz force law for a charged particle in a uniform magnetic field, since the magnetic field is a component in both equations. With BB-S as the magnetic field in the Biot-Savart law, and BL as the magnetic field in the Lorentz force law, by extrapolation to the corresponding equations for a charged point particle of 5D-size, we can write them as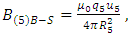 | (20) |
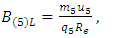 | (21) |
respectively, where B(5)B-S is the magnetic field of the Biot-Savart law in the fifth-dimensional size, B(5)L is the magnetic field of the Lorentz force law in the fifth-dimensional size, and u5 is the component of 5-velocity along the fifth-dimensional framework. Equating both magnetic fields from Eqs. (20) and (21) as a “common” term, yields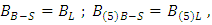 | (22) |
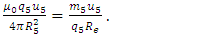 | (23) |
Let us consider the case in which the distance that the charge of 5D-size moves due to the effect of the Lorentz force is the same distance as the radius R5. Then, the space (either an area or a volume) that the mass m5 travels without movement or vibration will be limited to the distance R5 (i.e., Re → R5). Thus, we will have a static condition for the charged point particle of 5D-size (without vibration) in the five-dimensional frame, and Eq. (23) becomes as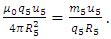 | (24) |
Solving for the rest mass, yields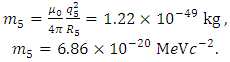 | (25) |
The ratio between electron rest mass (me) and rest mass (m5) of the point particle of five-dimensional size remains the same than in Eqs. (14) and (19), resulting 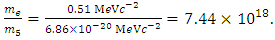 | (26) |
4. The Angular Momentum of a Charged Point Particle of Five-Dimensional Size Rotating in an External Magnetic Field
Planck’s equation for kinetic energy of a particle (like that of the photon) with angular frequency ω = 2πf, is expressed in terms of the reduced Planck’s constant as Ek = ℏω. Angular frequency is also considered in both, the Lorentz force law and the Cyclotron resonance frequency (that describes a simple harmonic-oscillator at the cyclotron frequency) [15,16] for a charged particle q with rest mass m rotating in an external magnetic field B, given as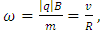 | (27) |
where v is the velocity of the particle. Furthermore, the relation between kinetic energy (when a particle is in motion) and Hamiltonian momentum given as Ek = p2/2m, where p = mv is the momentum of the charged particle in motion. Let us consider a test charged point particle of 5D-size in motion in an external magnetic field. It should behave analogously to the 4D charged particles in an external magnetic field. Extrapolating those equations to the scenario of a charged point particle of 5D-size rotating with a radius equivalent to the radius of the electron around the z-axis in an external magnetic field (neglecting its interaction with other particles of the atom), and rearranging the equivalent equation to find the reduced Planck’s constant, one gets the corresponding parameters as 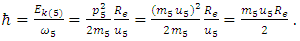 | (28) |
And reordering, yields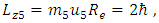 | (29) |
where Lz5 is the angular momentum component along the z-axis for the rotating charged particle of five-dimensional size. This result agrees with the quantization of angular momentum of a 4D charged particle, which is quantized in units of ħ. This also satisfies the Dirac model [17], where the considered value for the electron is 2 (and the value experimentally measured for the electron is approximately ge ≈ 2.00232…) [18]. Moreover, according to this extrapolation, the estimated values can be extrapolated to quantum mechanics to obtain the position, spin and orbital angular momentum of a corresponding particle related to the “relativistic” electron [19,20]. In this way, a charged point particle of 5D-size under these conditions would orient its angular momentum parallel to the external magnetic field (see Figure 1). 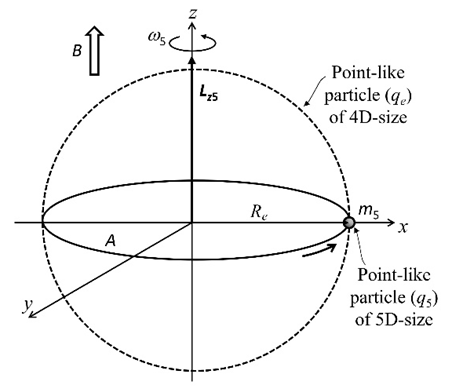 | Figure 1. Representation of the perspective of a charged point particle (q5) of five-dimensional size and rest mass (m5) interacting with the external magnetic field (B), moving with velocity u5 to cover a circular area (A) of the spherical volume of radius Re to form a spinning electron. Lz5 = 2ħ is the angular momentum along the z-axis for the rotating charged point particle in the five-dimensional framework |
In this model, the charged point particle of five-dimensional size that would give rise to the positron will correspond to a particle with an electric charge equivalent to q5, but rotating with an angular frequency in the opposite direction (that is, -ω5), according to the sign for the estimation of the energy of 5D-size, which we can write as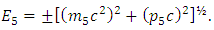 | (30) |
Thus, the sign of the resulting positron’s electric charge with respect to the same magnetic field will be opposite to that of the charged point particle of five-dimensional size related to the electron. Furthermore, the kinetic energy of a charged point particle of 5D-size with velocity u5 in a magnetic field can be written as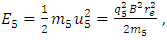 | (31) |
where re is the radius in which the energy to be determined. According to Eq. (28), we can write the total energy (kinetic energy and potential energy) for a rotating charged point particle of five-dimensional size, as | (32) |
Considering the harmonic-oscillator, this equation is analogous to the one derived by another method in early String theory [21], but in this case is for the frequency of the harmonic-oscillator of a point particle of 5D-size in circular motion (see Figure 1). In this stage, we can find an analogy between this model and early String theory (at least in the 5D context). However, we can consider that a closed string could only be possible in a static universe, since due to the propagation of time (in an expanding universe), any particle would not return to the exact same place in space-time from which it began. In this way, only the existence of open strings in the dynamics of space-time can be possible, covering a space that would resemble a volume through time (see Figure 2).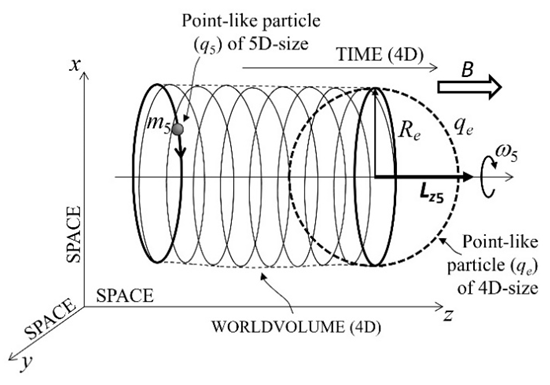 | Figure 2. Representation of the effect over time of the small particle of 5D-size rotating in a magnetic field to cover the space of a particle perceived in 4D (like a spinning electron) |
5. Radius, Electrical Charge and Rest Mass of Charged Point Particles of Five-Dimensional Size of Some Fermions
Extending the same analysis and applying Eqs. (12), (18) and (25), respectively, to some other fermions, in particular, spin 1/2 particles, and having their respective radius, charge and rest mass [22-24], we can calculate the respective characteristic values for the considered point particles of five-dimensional size. Those point particles must form each one of these particles when they are rotating with a radius equivalent to the radius Rf of the respective fermion around the z-axis in an external magnetic field. In this way, Table 1 is formed showing the respective values of each corresponding particle of 5D-size.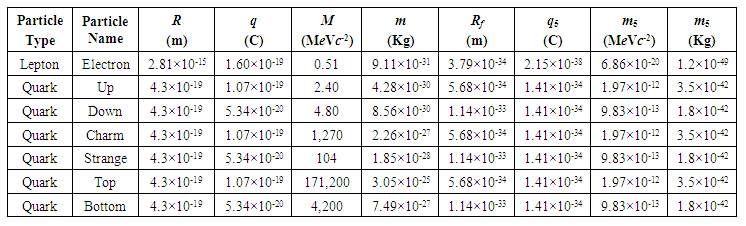 | Table 1. Corresponding characteristic values of point particles of five-dimensional size of some fermions |
6. Discussion and Conclusions
This work aims to explore a noncompactified model of a charged particle of five-dimensional size in an external magnetic field, considering the electrogravitational coupling constant. In this scenario, a particle of 5D-size is occupying a very small region in space-time, estimating the radius to be approximately 7.4×1018 smaller than the radius of the electron. The angular momentum of the charged particle along the z-axis in the five-dimensional scale results to be 2ħ. This result may explain the origin of the measured value of the gyromagnetic ratio of the electron. Extending the same analysis to some other charged particles of the Standard Model (such as fermions), the respective characteristic values of these charged point particles of five-dimensional size can be calculated. According to these results, considering that the up quark is a particle with a stable half-life, it must be formed by a charged point particle of five-dimensional size by a factor 106 smaller than the mass of the electron neutrino. This could be one of the best options for the detection of some of these considered small point particles of 5D-size. This could be the next step in the development of particle detectors with sufficient capacity to detect charged point particles of such a small scale.
ACKNOWLEDGEMENTS
The author would like to thank Professor Sergio S. Cornejo for its review and comments about this work.
References
| [1] | Kaluza, T. 1921 Zum Unitätsproblem in der Physik. Sitzungsber. Preuss. Akad. Wiss. Berlin. (Math. Phys.), 966. |
| [2] | Klein, O. 1926 Quantentheorie und fünfdimensionale Relativitätstheorie. Zeit. Phys. 37, 895. |
| [3] | Klein, O. 1926 The Atomicity of Electricity as a Quantum Theory Law. Nature 118, 516. |
| [4] | Finn, R. 2011 Oskar Klein and the fifth dimension. Contribution to the 250 years celebration of the Transactions of the Royal Norwegian Society of Sciences and Letters, No.4. |
| [5] | Sandoval-Villalbazo, A., García-Perciante, A.L., García-Colín, L.S. 2003 Oskar Klein, the sixth dimension and the strength of a magnetic pole. E-print: arXiv: gr-qc/0303097. |
| [6] | Van Dongen, J. 2002 Stud. Hist. Philos. Mod. Phys. 33(2), 185-210. |
| [7] | Bleecker, D. 1982 Gauge Theory and Variational Principles, Dover Publications. |
| [8] | Jordan, P. 1947 Erweiterung der projektiven Relativitätstheorie. Ann. Phys. Leipzig, 1, 219. |
| [9] | Thiry, M. Y. 1948 Les équations de la théorie unitaire de Kaluza. Compt. Rend. Acad. Sci. Paris, 226: 216-218. |
| [10] | Scherrer, W. 1949 Über den Einfluss des metrischen Feldes auf ein skalares Materiefeld. Helv. Phys. Acta. 22: 537-551. |
| [11] | Pigeaud, P. 1961 Séminaire Janet. Mécanique analytique et mécanique céleste 5: 1-10. |
| [12] | Williams, L. L. 2020 Field Equations and Lagrangian of the Kaluza Energy-Momentum Tensor. Adv. Math. Phys., Vol. 2020, Article ID 1263723. |
| [13] | Kalinowski, M. W. 2018 Fermion fields in the (non)symmetric Kaluza–Klein theory, Canadian Journal of Physics 96(5). |
| [14] | Tsokosdel, K. 1983 Stability and fermions in Kaluza-Klein theories, Phys. Lett. B, 126 (6): 451-454. |
| [15] | Chen, F. F. 1984 Introduction to Plasma Physics and Controlled Fusion, Plasma Physics, 2nd Ed. Vol. 1, Plenum Press, NY. |
| [16] | Seidel, M. 2021 Cyclotrons and Fixed Field Alternating Gradient Accelerators. Contribution to the CERN Accelerator School. E-print: arXiv: 2105.04477v3 [physics.acc-ph]. |
| [17] | Dirac, P.A.M. 1928 The quantum theory of the electron. Proc. R. Soc. Lond. A, 117. |
| [18] | Odom, B., et al. 2006 New Measurement of the Electron Magnetic Moment Using a One Electron Quantum Cyclotron. Phys. Rev. Lett. 97(3): 030801. |
| [19] | Konstantin, Y. B. 2011 Relativistic Electron Vortex Beams: Angular Momentum and Spin-Orbit Interaction. Phys. Rev. Lett. 107, 174802. |
| [20] | Konstantin, Y. B. 2017 Position, spin and orbital angular momentum of a relativistic electron. Phys. Rev. A 96, 023622 |
| [21] | Susskind, L. 1969 Harmonic oscillator analogy for the Veneziano amplitude. Phys. Rev. Lett. 23 (10): 545-547. |
| [22] | Abramowicz, H. et al. 2016 Limits on the effective quark radius from inclusive ep scattering at HERA, Phys. Lett. B 757, 468-472. |
| [23] | Wang, S. et al. 2020 Radial distribution of charm quarks in jets in high-energy heavy-ion collisions. Elsevier, Nuclear Physics A 00, 1-4. |
| [24] | Wang, S. et. al. 2021 Radial profile of bottom quarks in jets in high-energy nuclear collisions. Chinese Physics C 45(6), p 064105. |



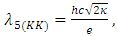
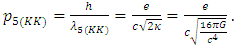
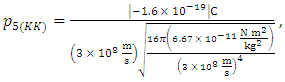
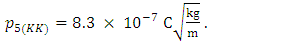
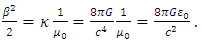
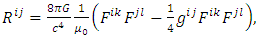
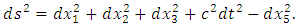
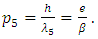
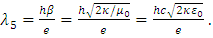
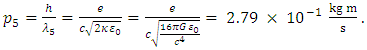
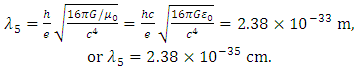
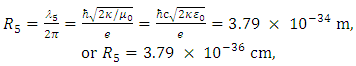
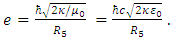
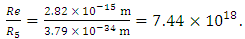
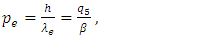
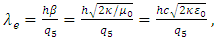
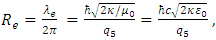
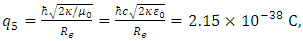
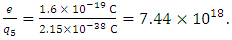
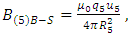
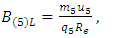
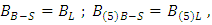
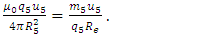
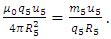
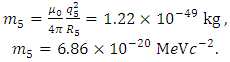
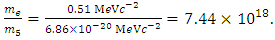
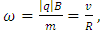
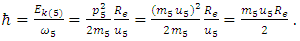
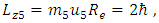
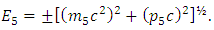
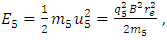



 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML