1. Introduction

In [1,2], the proposition was put forth that so-called Dark Matter (DM) in whole, or part, is comprised of gravitational solitons (i.e, “gravisolitons” [1]). Specifically in [1], it is mathematically shown that gravisolitons can exist in the so-called weak gravitational field case—precisely the case encountered when considering DM distributions around galaxies. Somewhat ironically, this is the domain where Newtonian models are assumed to apply, yet they do not predict the existence of space-time gravisolitons. So, even in the “non-exotic” case, General Relativity (GR) has much to teach. [2] proposes that the requisite “astronomical” amounts of energy to create DM was derived from the Big Bang. While linear gravitational waves propagate at the speed of light, nonlinear waves in general, and solitons in particular, can travel at subluminal speeds (slower than the speed of light). Thus, allowing time for their symbiotic coupling with ordinary matter [1-3].

In this paper, an elemental constructive proof is developed that shows how gravisolitons can form stable orbits around ordinary matter consistent with the weak field limit as detailed in [1]. Moreover, it is also shown that the unique properties of solitons allow for fully 3D “halos” of DM around disc galaxies—for which ordinary matter evolves into a 2D distribution. Something that cannot be explained if DM consists of particles with mass.

The remaining paper is organized as follows: In Section 2, an elemental constructive proof is provided that shows how gravisolitons can form stable orbits around ordinary matter. The proof is based on basic principles of GR and does not require extensive analytical or numerical solutions of the field equations. Section 3 then invokes fundamental properties of soliton wave mechanics to show how fully 3D halo like structures can form even around disc galaxies. Section 4 discusses the Big Bang origins of gravisolitons as discussed in [2]. Lastly, in Section 5, a general discussion of the ramifications of this result are presented, along with its potential to predict new astronomical observational results. This section concludes with a discussion of other nonlinear GR wave phenomenon that can explain recent observations on the general distribution of DM throughout the universe.

2. A Constructive Proof for the Gravisoliton Theory of Dark-Matter

Consider Fig. 1 (a)-(d). It addresses the case when a small test mass 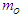, and a curvature wave packet (CWP) 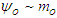, whose space-time curvature is commensurate with the small test mass [4], as viewed from an inertial reference frame, are in either free-space (a)-(b), or within the gravitational influence of a larger non-rotating mass M (c)-(d). Of particular interest is the case represented by a central galactic mass, with exo-galactic distances commensurate with observed DM distributions, particularly of the “halo” type [5]. Each graph depicts events at 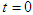, and finite time later 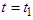. Results can be extended to a rotating large mass in a straightforward manner.

Fig. 1 (a) and (c) are obvious based on basic Newtonian physics. Fig. 1 (a) is governed by Newton’s First Law, while Fig. 1 (c) is governed by Newton’s Law of Gravity for the case when the gravity of the large mass (at the origin) is sufficient to capture a passing by small mass with an appropriate range of orbital capture velocities [6].

Fig. 1 (b) considers the case when a small space-time curvature wave packet (CWP) , whose curvature is commensurate with the small test mass, is present at time 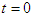. The governing GR equations are the homogenous Einstein Field Equations (EFE) given by

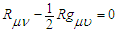(1)

where and R are the Ricci tensor and curvature tensor respectively, 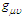is the Einstein tensor [4]. For the mass-energy free homogenous case, a 3+1 foliation of the EFE yields homogenous second order differential equations similar to Maxwell’s equations in free space with a wave propagation speed equal to the speed of light [7]. This, of course, is what has led to the prediction of gravitational waves [8].

Returning to Fig. 1 (b), and the governing dynamical equations (a foliation of (1)), we see that any initial perturbation (in this a localized CWP) will disperse in all directions at the speed of light c.

The situation in Fig. 1 (d) is completely different when mass-energy is present in sufficient quantity and proximity to a CWP. In this case, the full nonlinear EFE are in play:

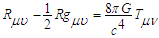(2)

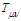where is the stress-energy tensor, G is the Newtonian gravitational constant, and c is the speed of light (consistent units assumed). In both [1,3], it is shown that under realizable conditions, a sustainable nonlinear wave phenomenon dubbed a gravisoliton, is allowable by the EFEs. The exact conditions depend, as one would expect, on the large mass M, and the distance to the test point (which affects the degree of space-time curvature in proximity to the test point). In this case, 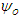can be replaced with a soliton (or gravisoliton), with a subliminal propagation velocity v again commensurate with the previously stated capture velocities. GR dictates that any kinematics must obey a geodesic (principle of lest action) [4]. Thus 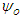must follow a trajectory commensurate with the equivalent test mass . If a circular orbit is achieved, then the requisite conditions for sustaining a soliton solution will persist indefinitely. This elemental constructive proof further bolsters the DM gravisoliton theory proposed in [1,2].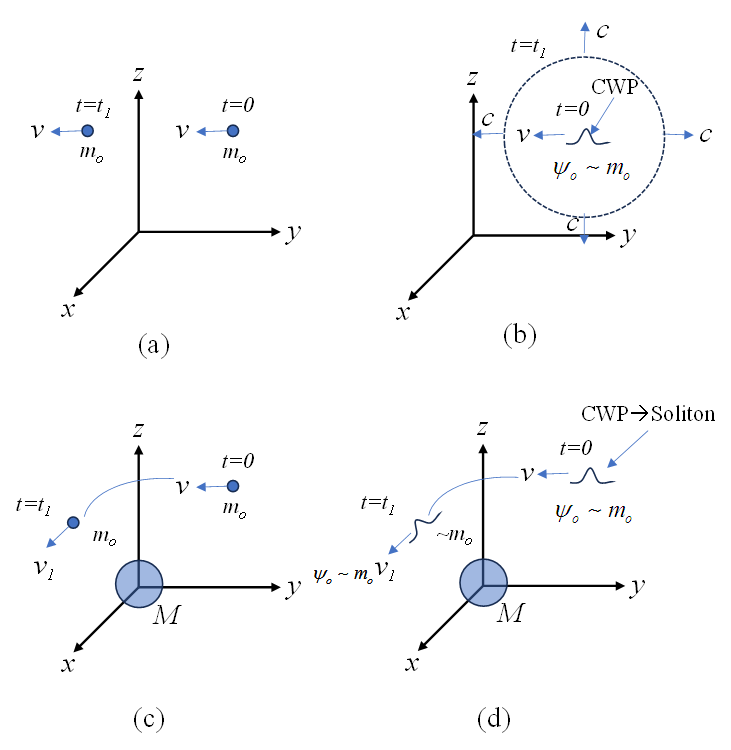

Figure 1. Illustration of how gravisolitons can form stable orbits around ordinary matter

3. DM Halos Around Disc Galaxies

One of the key defining features of solitons in general, and gravisolitons in particular, is that they emerge from collisions with other solitons unscathed—except for a phase change that does not affect the shape and stability [3]. This explains how “swarms” of solitons can form fully 3D halos around otherwise 2D disc galaxies—something any massive particle (e.g., WIMPs) cannot sustain (over millions of years) due to both internal DM collisions and interactions with the ordinary matter (OM) in the galaxy.

Interestingly, the soliton collision stability does not hold for interactions with OM. Thus, it is conjectured that the “interface” between the 3D DM halo, and the OM of the galaxy should be generally devoid of DM. Something that may be observed astronomically in the future (see Fig. 2).

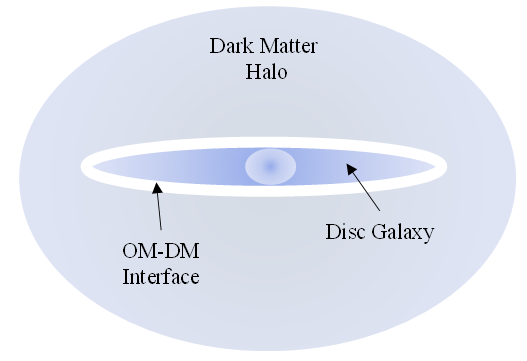Figure 2. Illustration of potential OM-DM interface in a disc galaxy

4. Origin of DM Gravisolitons

As argued in [2], the origin of DM was ultimately the Big Bang. It was the “mother” of all nonlinear GR wave phenomenon. An inconceivable variety of space-time nonlinear waves were launched, most of which, at least initially, would be propagating at subliminal speeds (non-free space propagation). This allows ample time for these waves to interact with ordinary matter to form the stabilizing structures we now observe. The uncanny stability properties of gravisolitons explains its persistence to current day (along with the previously presented constructive proof).

5. Other Nonlinear GR Wave Phenomenon and Areas for Future Investigations

Recent astronomical observations, though preliminary, seem to indicate a complicated morphology for the distribution of DM [9]. In addition to gravisolitons, there are other well known stable nonlinear wave phenomenon such as vortices. This is an area for future investigations [10].

In this paper, an elemental constructive proof is presented that shows how gravisolitons can form stable 3D orbital dark matter (DM) structures around ordinary matter (OM). Further bolstering the theory that DM consists largely or entirely of gravisolitons and/or other nonlinear wave phenomena. The uncanny stability properties explain its ability to form stable 3D halo structures around otherwise 2D disc galaxies. The Big Bang provided the requisite “launching” energies and morphological distributions to account for the large amounts of DM in the universe.

Although an important fundamental step, the proof provided herein raises many areas for future investigations including the exact nature (size, shape, etc.) of the constitutive gravisolitons and their distribution in a 3D halo. Current gravisoliton theory shows that the morphology changes with distance from the accompanying OM center. This suggests a non-homogenous distribution of solitons with distance from the galactic center, again something which may be observed in the future. This will most likely require new numerical relativity methods due to the highly nonlinear nature of the EFEs in such situations.