-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Astronomy
p-ISSN: 2169-8848 e-ISSN: 2169-8856
2022; 11(1): 5-8
doi:10.5923/j.astronomy.20221101.02
Received: Jun. 13, 2022; Accepted: Jul. 4, 2022; Published: Jul. 15, 2022

General Relativity, Solitons, and Dark Matter
Joseph R. Guerci, Robert W. Schutz
Information Systems Laboratories, Inc., San Diego, CA, USA
Correspondence to: Joseph R. Guerci, Information Systems Laboratories, Inc., San Diego, CA, USA.
| Email: |  |
Copyright © 2022 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This paper puts forth the proposition that Dark Matter (DM) is in fact gravitational solitons originally forged in the Big Bang and sustained by their nonlinear interaction with ordinary matter of sufficient density and distribution to achieve the requisite nonlinear space-time manifold required for soliton or nonlinear stationary wave solutions. This hypothesis is supported by the following facts and/or reasonable deductions: (1) Einstein’s field equations (EFEs) admit soliton solutions (gravisolitons); (2) Gravitational solitons of sufficient launching energy were likely in abundance during the early evolution of the Big Bang due to the highly energetic and nonlinear nature of the primordial space-time manifold; (3) These solitons have gravitational attraction; (4) Current astronomical observations indicate Dark Matter is only observed in the presence of of ordinary matter and it is not found in galaxies that are sparsely populated or in space devoid of significant matter. Unlike the search for the elusive Dark Matter “particle”, the soliton hypothesis can be verified through computer simulation and current astronomical observations. The paper ends by detailing two computer experiments that can be performed to confirm the hypotheses.
Keywords: Dark Matter, General Relativity, Einstein’s Field Equations (EFE), Solitons, Big Bang, Gravisolitons
Cite this paper: Joseph R. Guerci, Robert W. Schutz, General Relativity, Solitons, and Dark Matter, International Journal of Astronomy, Vol. 11 No. 1, 2022, pp. 5-8. doi: 10.5923/j.astronomy.20221101.02.
Article Outline
1. Introduction
- Dark Matter represents one of the biggest conundrums facing cosmologists and astrophysicists since its gravitational effects are clearly observed through the motions of galaxies and gravitational lensing [1], yet there is apparently no “ordinary” matter (or energy) present. Moreover, the amount of energy that would be required to create such gravitational effects if no mass was present would be so enormous that it too would be clearly visible through various observational means. Conventional gravitational waves of enormous energy can also be ruled out since they travel at generally the speed of light and would thus not be able to persist in locations where large amounts of ordinary mass is present (e.g., galaxies). All of this (and more) has led researchers to posit the existence of a yet undiscovered form of matter, i.e., Dark Matter [2,3].However, there is another possibility allowed by Einstein’s General Relativity (GR), gravitational solitons. Indeed there is an entire book dedicated to this phenomenon (see Belinski, et al., [4]). Also, very recently (2020) Asselmeyer-Maluga and Król [5] have shown that gravitational solitons can persist under certain highly specific conditions that can be found in the cosmos. However, the existing soliton literature focuses on highly specialized formulations and simplifications that are amenable to efficient numerical or analytical techniques such as the inverse scattering method (ISM) [4]. In contrast, this paper works “backwards” by using the existing morphology of dark matter and ordinary matter (such as in a galaxy) as an “ansatz” to Einstein’s field equations. There is no expectation that the solutions will be analytical. Rather numerical integration will need to be performed, such as the techniques of Numerical Relativity [6].In summary, this paper proposes that so-called Dark Matter is in fact comprised gravitational solitons (or gravisolitons using the terminology of [5]) originally forged in the Big Bang and sustained by their nonlinear interaction with ordinary matter-energy of sufficient density and distribution (and possible combining with other gravisolitons). The connection to the Big Bang, and the symbiotic relationship between the soliton and the embedded ordinary matter-energy to achieve the requisite balanced and sustainable nonlinear conditions, are the key insights. The rest of the paper delves further into this theory and its consequences including verifiable predictions. Lastly, two computer experiments involving Einstein’s field equations and current astronomical observations are discussed to verify both the steady state and launching process of gravisolitons.
2. Gravitational Solitons and Einstein’s Field Equations
- The first documented observation of a soliton was by Civil Engineer John Scott Russell in 1834 [7], and was later put on a firm theoretical and mathematical footing [8]. While the theory of solitons is quite rich, we will just focus on the salient elements relevant to our discussion.Solitons are solutions to certain types of nonlinear partial differential equations. These localized “wave packet” like structures have unique properties that set them apart from ordinary waves. They can, for example, persist far longer than ordinary waves provided that the medium they are in retains a certain balancing of somewhat competing nonlinear and dispersive effects [9]. Lastly, they do not interact with other solitons in the same manner as ordinary waves. Indeed, one of the most exotic features of solitons is that when they collide, they can form complex transient structures but nonetheless emerge virtually unscathed and retain their original forms—further strengthening their unique ability to persist. However, unlike ordinary solitons, gravisolitons have gravitational attraction. It is thus an open question as to how gravitational solitons interact amongst themselves. It is not unreasonable to assume that under certain conditions gravisolitons can combine. Indeed, this could explain how such an enormous amount of Dark Matter persists to present day.Analytical forms of solitons for simplified nonlinear cases have been known since 1895 [8]. For example, the KdV equation has the form
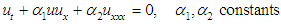 | (1) |
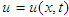 denotes the height from the average medium surface (water, space-time), x is the direction of movement, subscripts t and x denote partial differentiation with respect to time and space (respectively). A solution to (1) is given by
denotes the height from the average medium surface (water, space-time), x is the direction of movement, subscripts t and x denote partial differentiation with respect to time and space (respectively). A solution to (1) is given by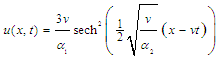 | (2) |
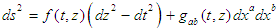 | (3) |
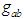 is non-diagonal—that is the key necessary nonlinear ingredient to allow for soliton solutions. They then use the ISM method to produce a soliton solution. This is a very important and fundamental result that firmly establishes the feasibility of gravisolitons even in relatively weak gravitational fields. This result is consistent with astronomical observations that have found dark matter in just such regions (e.g., a dark matter “halo” surrounding a galaxy).The key difference in this paper is that, unlike [5]: (a) we adopt an “observations as ansatz” approach wherein we suppose that the dark matter distributions experimentally observed are nonlinear stationary waves and that if true, they should result in stable solutions when directly plugged into the EFEs, with no simplifications; and (b) the enormous amount of energy required to create such waves was supplied by the Big Bang. To date, constructive methods have been employed to determine the conditions under which the EFEs yield the requisite partial differential equation (PDE) structures that are amenable to well-behaved numerical solution methods such as the inverse scattering method (ISM) [10]. This of course has the advantage of rigorously proving the existence of gravisolitons, but it no way guarantees that it will find ALL gravisoliton solutions. Indeed, the premise of this paper is that astronomical observations of dark matter (accompanied by ordinary matter) are empirical proof of other forms of gravisolitons that may or may not be amenable to current analytical methods, but which nonetheless must be solutions to the EFEs. The major elements of the Dark Matter gravisoliton (DMGS) hypothesis are:• Dark Matter, as observed astronomically, is in fact gravisolitons sustained via a unique symbiotic relationship with ordinary matter of sufficient amount, density, and morphology. This is why Dark Matter is not observed in regions of space devoid of matter (and gravity) and/or in galaxies of insufficient mass such as NGC 1052-DF [11].• Gravisolitons warp space-time in a manner similar to ordinary matter and thus have gravitational attraction. This property is of course unique to gravisolitons and is not a feature of solitons in general. This attraction is key to the sustainment of the gravisoliton: it attracts matter, matter attracts gravisoliton and provides the necessary additional space-time nonlinearity required for a soliton to exist and persist in the EFEs. Moreover, unlike ordinary solitons that do not naturally combine, gravisolitons might be able to do so due to their mutual gravitational attraction. This is a major area for future research (see Section III). • Gravisolitons do not generally travel at the speed of light as do ordinary gravitational waves. Their group velocity depends on soliton parameters. Without this property they could not coexist with ordinary matter (and perhaps other gravisolitons). • The gravisolitons observed today are remnants of ancient solitons formed in the Big Bang. The highly energetic nonlinear nature of the early universe makes it plausible that all manner of gravisolitons were initially created. Only those that combined with potentially other gravisolitons and ultimately with the requisite ordinary mass/mass-distribution persisted to achieve the symbiotic steady-state structures described above and observed today.The above is consistent with current astronomical observations such as the fact that Dark Matter is not found everywhere in the universe. And that, moreover, it seems to only be found in the presence of ordinary matter. The gravitational attraction of gravisolitons, and the need to create a symbiotic nonlinear balancing with ordinary matter, explain these observations.
is non-diagonal—that is the key necessary nonlinear ingredient to allow for soliton solutions. They then use the ISM method to produce a soliton solution. This is a very important and fundamental result that firmly establishes the feasibility of gravisolitons even in relatively weak gravitational fields. This result is consistent with astronomical observations that have found dark matter in just such regions (e.g., a dark matter “halo” surrounding a galaxy).The key difference in this paper is that, unlike [5]: (a) we adopt an “observations as ansatz” approach wherein we suppose that the dark matter distributions experimentally observed are nonlinear stationary waves and that if true, they should result in stable solutions when directly plugged into the EFEs, with no simplifications; and (b) the enormous amount of energy required to create such waves was supplied by the Big Bang. To date, constructive methods have been employed to determine the conditions under which the EFEs yield the requisite partial differential equation (PDE) structures that are amenable to well-behaved numerical solution methods such as the inverse scattering method (ISM) [10]. This of course has the advantage of rigorously proving the existence of gravisolitons, but it no way guarantees that it will find ALL gravisoliton solutions. Indeed, the premise of this paper is that astronomical observations of dark matter (accompanied by ordinary matter) are empirical proof of other forms of gravisolitons that may or may not be amenable to current analytical methods, but which nonetheless must be solutions to the EFEs. The major elements of the Dark Matter gravisoliton (DMGS) hypothesis are:• Dark Matter, as observed astronomically, is in fact gravisolitons sustained via a unique symbiotic relationship with ordinary matter of sufficient amount, density, and morphology. This is why Dark Matter is not observed in regions of space devoid of matter (and gravity) and/or in galaxies of insufficient mass such as NGC 1052-DF [11].• Gravisolitons warp space-time in a manner similar to ordinary matter and thus have gravitational attraction. This property is of course unique to gravisolitons and is not a feature of solitons in general. This attraction is key to the sustainment of the gravisoliton: it attracts matter, matter attracts gravisoliton and provides the necessary additional space-time nonlinearity required for a soliton to exist and persist in the EFEs. Moreover, unlike ordinary solitons that do not naturally combine, gravisolitons might be able to do so due to their mutual gravitational attraction. This is a major area for future research (see Section III). • Gravisolitons do not generally travel at the speed of light as do ordinary gravitational waves. Their group velocity depends on soliton parameters. Without this property they could not coexist with ordinary matter (and perhaps other gravisolitons). • The gravisolitons observed today are remnants of ancient solitons formed in the Big Bang. The highly energetic nonlinear nature of the early universe makes it plausible that all manner of gravisolitons were initially created. Only those that combined with potentially other gravisolitons and ultimately with the requisite ordinary mass/mass-distribution persisted to achieve the symbiotic steady-state structures described above and observed today.The above is consistent with current astronomical observations such as the fact that Dark Matter is not found everywhere in the universe. And that, moreover, it seems to only be found in the presence of ordinary matter. The gravitational attraction of gravisolitons, and the need to create a symbiotic nonlinear balancing with ordinary matter, explain these observations.3. Computer Experiment I (CE-I): Steady State
- This first experiment is to validate the steady state hypotheses that currently observed matter-energy/Dark Matter distributions are in fact steady state gravisoliton solutions. That is, they represent a steady-state symbiotic relationship between gravisolitons and ordinary matter that is self-sustaining. The basic idea is to seed Einstein’s field equations with the observed matter and Dark Matter distribution for a typical galaxy, then proceed with the numerical integration to determine if the combined matter-gravisoliton solution persists (i.e., is self-sustaining). Since the EFEs present enough of a challenge in and of themselves, it is reasonable to begin with as simple a known existing exemplar (or ansatz) from astronomical observations, such as a circular dwarf galaxy [12]. The 3+1 method of Numerical Relativity is an ideal approach for this experiment. Details can be found in [6].Einstein’s field equations in compact tensor form are given by [13]
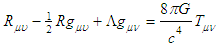 | (4) |
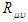 and R are the Ricci tensor and curvature tensor respectively,
and R are the Ricci tensor and curvature tensor respectively, 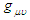 is the Einstein tensor,
is the Einstein tensor, 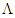 is the cosmological constant,
is the cosmological constant, 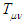 is the stress-energy tensor, G is the Newtonian gravitational constant, and c is the speed of light (consistent units assumed). In this elegant compact tensor form the left-hand side (LHS) pertains to the properties (curvature) of space-time, while the right-hand side (RHS) pertains to mass-energy. Note that when dealing with celestial objects on the order of galaxies or less, the cosmological constant term is usually ignored. Whether or not this approximation is also valid for gravisoliton analysis is an open question.Setting up the RHS of (4) (i.e.,
is the stress-energy tensor, G is the Newtonian gravitational constant, and c is the speed of light (consistent units assumed). In this elegant compact tensor form the left-hand side (LHS) pertains to the properties (curvature) of space-time, while the right-hand side (RHS) pertains to mass-energy. Note that when dealing with celestial objects on the order of galaxies or less, the cosmological constant term is usually ignored. Whether or not this approximation is also valid for gravisoliton analysis is an open question.Setting up the RHS of (4) (i.e., 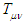 ) for a given galaxy exemplar is “relatively” straightforward given the astronomical observations of ordinary matter and reasonable interpolations and extrapolations. The LHS is more subtle, and pertains to the space-time morphology and magnitude of the combined matter and gravisoliton (e.g., Dark Matter). Initial conditions for
) for a given galaxy exemplar is “relatively” straightforward given the astronomical observations of ordinary matter and reasonable interpolations and extrapolations. The LHS is more subtle, and pertains to the space-time morphology and magnitude of the combined matter and gravisoliton (e.g., Dark Matter). Initial conditions for 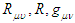 need to be selected to match the observed and estimated distribution of Dark Matter and ordinary matter since both shape space-time. That is space-time must morphed via the LHS into a shape that matches observations. To simplify things further, a known galaxy exemplar should be chosen that is not only relatively simple in its own right, but which is far enough removed from other galaxies/matter so that the spatial boundary conditions in the EFEs are greatly simplified. Complexity can always be added over time. The point is, if gravisolitons cannot be verified for the “easiest” known cases, there is no need to look any further.Interestingly, Newtonian gravity can be used to first estimate the distribution of Dark Matter. For example, it is possible to estimate the spatial distribution of Dark Matter required to match astronomical observations of galactic rotation, i.e., the amount of “invisible” matter required to allow outer bands of the galaxy to rotate at the same rate as its inner portions. However, unlike Newtonian gravity, the Dark Matter mass estimates are used on LHS, not the RHS of (4) when conducting numerical relativity experiments. This is the key to the whole theory of gravisoliton Dark Matter. WIMPS belong on the RHS of (4). In [5], the authors propose that dark matter may be a combination of WIMPS and gravisolitons.Again, the spirit of this computer experiment is to assume a priori that the combined Dark Matter and ordinary matter galaxy being observed is a gravisoliton solution to the EFEs—and then test the hypothesis. This is unlike the references cited that work to find analytically the conditions under which the EFEs can be manipulated into a form amenable to known soliton cases (using for example the aforementioned ISM methods). It is not at present obvious how to extend these simplified analytical methods to real-world dark matter distributions. Hence the need for numerical relativity methods.Lastly, it is essential that these numerical experiments be conducted by completely independent scientists using independently developed software to bolster confidence of the results.
need to be selected to match the observed and estimated distribution of Dark Matter and ordinary matter since both shape space-time. That is space-time must morphed via the LHS into a shape that matches observations. To simplify things further, a known galaxy exemplar should be chosen that is not only relatively simple in its own right, but which is far enough removed from other galaxies/matter so that the spatial boundary conditions in the EFEs are greatly simplified. Complexity can always be added over time. The point is, if gravisolitons cannot be verified for the “easiest” known cases, there is no need to look any further.Interestingly, Newtonian gravity can be used to first estimate the distribution of Dark Matter. For example, it is possible to estimate the spatial distribution of Dark Matter required to match astronomical observations of galactic rotation, i.e., the amount of “invisible” matter required to allow outer bands of the galaxy to rotate at the same rate as its inner portions. However, unlike Newtonian gravity, the Dark Matter mass estimates are used on LHS, not the RHS of (4) when conducting numerical relativity experiments. This is the key to the whole theory of gravisoliton Dark Matter. WIMPS belong on the RHS of (4). In [5], the authors propose that dark matter may be a combination of WIMPS and gravisolitons.Again, the spirit of this computer experiment is to assume a priori that the combined Dark Matter and ordinary matter galaxy being observed is a gravisoliton solution to the EFEs—and then test the hypothesis. This is unlike the references cited that work to find analytically the conditions under which the EFEs can be manipulated into a form amenable to known soliton cases (using for example the aforementioned ISM methods). It is not at present obvious how to extend these simplified analytical methods to real-world dark matter distributions. Hence the need for numerical relativity methods.Lastly, it is essential that these numerical experiments be conducted by completely independent scientists using independently developed software to bolster confidence of the results. 4. Computer Experiment II (CE-II): Launching and Transient Analysis
- A confirmation of the steady state gravisoliton solution from Computer Experiment I (CE-I) represents a significant breakthrough in its own right: Gravisolitons explain astronomically observed Dark Matter. As with all science, answering one questions raises many others, such as “how were these gravisolitons created?”. This second computer experiment is designed to begin to chip away at this much harder question.The amount of Dark Matter observed is currently estimated to be much larger than the amount of ordinary matter (~80% of existing matter). Einstein’s famous energy mass equivalence
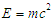 implies that gravisolitons represent an enormous amount of energy—energy that could only be explained by either: (1) the Big Bang (alone); or perhaps (2) an even more complex mechanism involving both the Big Bang and the merging of gravisolitons (unlike ordinary solitons) with other gravisolitons and ordinary matter over time. This second computer experiment is thus far more complex and ambitious to setup then the first (CE-I). The Big Bang birthing hypothesis for gravisolitons would require setting up conditions for the EFEs whereby a gravisoliton is launched into a maelstrom of primordial matter-energy and warped space-time. The hypothesis under test is that the mutual gravitational attraction between gravisolitons and ordinary matter-energy would begin the process of coalescing the combined object into a steady-state form as examined in CE-I. There is no reason to expect that such an experiment would work under all possible initial conditions. Thus, a search would need to be conducted to determine when the right conditions would be met. This would likely entail significant computer resources. An interesting “side” experiment would be to test whether gravisolitons can in fact combine given their mutual gravitational attraction and whether a new resultant gravisoliton could emerge. Assuming a positive outcome from CE-I, this would imply that the new combined gravisoliton also possesses enough ordinary matter-energy to sustain the requisite nonlinear conditions for solitons to exist. If this merging process was linear with respect to mass-energy (speculation), then the resultant should have enough mass-energy to sustain the larger gravisoliton.In closing, it is important to emphasize that there should be no expectation that gravisolitons as observed astronomically would lend themselves to analytical mathematical methods such as ISM. Hence the reliance (first) on numerical methods. Also, as previously mentioned, independently confirming these numerical results is essential.
implies that gravisolitons represent an enormous amount of energy—energy that could only be explained by either: (1) the Big Bang (alone); or perhaps (2) an even more complex mechanism involving both the Big Bang and the merging of gravisolitons (unlike ordinary solitons) with other gravisolitons and ordinary matter over time. This second computer experiment is thus far more complex and ambitious to setup then the first (CE-I). The Big Bang birthing hypothesis for gravisolitons would require setting up conditions for the EFEs whereby a gravisoliton is launched into a maelstrom of primordial matter-energy and warped space-time. The hypothesis under test is that the mutual gravitational attraction between gravisolitons and ordinary matter-energy would begin the process of coalescing the combined object into a steady-state form as examined in CE-I. There is no reason to expect that such an experiment would work under all possible initial conditions. Thus, a search would need to be conducted to determine when the right conditions would be met. This would likely entail significant computer resources. An interesting “side” experiment would be to test whether gravisolitons can in fact combine given their mutual gravitational attraction and whether a new resultant gravisoliton could emerge. Assuming a positive outcome from CE-I, this would imply that the new combined gravisoliton also possesses enough ordinary matter-energy to sustain the requisite nonlinear conditions for solitons to exist. If this merging process was linear with respect to mass-energy (speculation), then the resultant should have enough mass-energy to sustain the larger gravisoliton.In closing, it is important to emphasize that there should be no expectation that gravisolitons as observed astronomically would lend themselves to analytical mathematical methods such as ISM. Hence the reliance (first) on numerical methods. Also, as previously mentioned, independently confirming these numerical results is essential.5. Conclusions
- In summary, this paper proposes that so-called Dark Matter is in fact gravitational solitons originally forged in the Big Bang and sustained by their nonlinear interaction with ordinary matter-energy of sufficient density and distribution. The connection to the Big Bang, and the symbiotic relationship between the soliton and the embedded ordinary matter-energy to achieve the requisite balanced and sustainable nonlinear conditions, are the key insights. Two fundamental computer experiments involving Einstein’s field equations and current astronomical observations are discussed that can verify both the steady state and launching process of gravisolitons. Interestingly, the entire theory can be tested using existing astronomical observations and detailed computer analysis—no need for ever more elaborate particle accelerators and/or detectors.Lastly, to achieve requisite statistical confidence, it is critical that the computer experiments described herein be conducted by others in a completely independent manner, as is the case with any experiment.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML