-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Astronomy
p-ISSN: 2169-8848 e-ISSN: 2169-8856
2021; 10(2): 50-59
doi:10.5923/j.astronomy.20211002.03
Received: Nov. 1, 2021; Accepted: Nov. 24, 2021; Published: Dec. 15, 2021

Rotating Disk Cosmological Systems in the Lagrangian and Relativistic Solutions
Adrián G. Cornejo
Electronics and Communications Engineering from Universidad Iberoamericana, Santa Rosa 719, CP 76138, Querétaro, Mexico
Correspondence to: Adrián G. Cornejo, Electronics and Communications Engineering from Universidad Iberoamericana, Santa Rosa 719, CP 76138, Querétaro, Mexico.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This work is a review that summarizes the previous works that describe the theory in which the movement of some circular or disk cosmological systems, such as the entire disk of the Solar System and spiral galaxies, corresponds to the dynamics like a rigid body in rotational motion. It has been found that both the Lagrangian solution and the relativistic solution consider all the energies and forces involved in the rotating systems. On this assumption, we have been derived the respective equations to explain the apsidal precession of the planets, the Earth’s axial precession and the rotation curves of some spiral galaxies, all of them due to the effect of rotating systems like a rigid body in rotational motion. A good approximation between the calculated and the observations for each of these cases has been found. Thus, this theory unifies classical mechanics (through Lagrangian mechanics) with the solution of general relativity and its intrinsic consideration of the rigid body in rotational motion in the three-dimensional framework. Also, it unifies all these rotational behavior of these disk cosmological systems in the same concept of the rigid body in rotational motion.
Keywords: Solar system: General, Planet-disk interactions, Galaxies: spiral, Kinematics and dynamics, Lagrangian mechanics, General Theory of Relativity
Cite this paper: Adrián G. Cornejo, Rotating Disk Cosmological Systems in the Lagrangian and Relativistic Solutions, International Journal of Astronomy, Vol. 10 No. 2, 2021, pp. 50-59. doi: 10.5923/j.astronomy.20211002.03.
Article Outline
1. Introduction
- Newton’s law of gravitation [1,2] has been applied for hundreds of years with some success to explain several observed mechanical and astronomical phenomena, and it is still used to try to explain some problems in cosmology, although having some difficulties to provide an exact solution and confirm the measurements and observations in several cases.The issue is that the classical total force only considers two terms, which are the Newtonian gravitational force and the centrifugal force [2]. Then, it has some limitations proper of this classical theory since it does not consider any other energy or force involved in the rotating systems. This is the reason why is necessary to add some matter or forces to adjust the calculations to the rotational velocities observed in spiral galaxies, such as the dark matter concept [3], which has not been detected to date, or even develop some adjustments like the proposed in the Modified Newtonian Dynamics (MOND) theory [4,5]. The main problem with these considerations is that the rotation of spiral galaxies and the entire Solar System (as circular or disk cosmological systems) have not been well taken into account, even in most of the standard astronomical considerations. On the other hand, the net or absolute total force in the relativistic solution, which is derived from the General Theory of Relativity (GTR) [6], also considers a third additional term that includes the force related to the Coriolis force in a rotating system, which is inverse of the distance to the fourth power [7]. This is the main reason why the relativistic solution can be considered to provide an exact solution which does not require any additional matter and does not require any adjustment to fit to the rotational velocities observed in spiral galaxies.This work summarizes the previous works that describe the theory in which the movement of some circular or disk cosmological systems, such as the entire disk of the Solar System and spiral galaxies, they all behave like a rigid body in rotational motion. Through those works, it has been found that both, Lagrangian and relativistic solutions consider all the forces and energies involved in the rotating systems. On this assumption, have been derived the respective equations to explain the apsidal precession of the planets [8], the Earth’s axial precession [9,10] and the rotation curves of some spiral galaxies [11,12], if the gas is assumed to be a stable component of the galaxy, as described by the quasi-stationary density wave theory, which characterizes spirals as rigidly rotating, long-lived patterns (i.e. steady spirals) [13]. In the case of the barred spiral galaxies, the Kerr metric has been considered as part of the solution. Thus, the existence of barred spiral galaxies could be a confirmation of the Kerr metric. A good approximation between the calculated and the observations for each of these cases has been found. Thus, this theory unifies classical mechanics (through Lagrangian mechanics) with the solution of the general relativity in the three-dimensional framework. Also, it unifies all these rotational behavior of these disk cosmological systems in the same concept of the rigid body in rotational motion.Although there may be several independent investigations to date regarding the existence of the supposed dark matter by indirect detection (that is, attributing some observations to dark matter), so far this is a proposed conjecture and its existence has not yet been confirmed or directly detected to date, so that its existence cannot yet be categorically confirmed. Therefore, the other theories that do not require dark matter to explain the rotation curves observed in spiral galaxies, such as the one considered here, should not be ruled out.
2. Lagrangian Solution for the Total Force of the Rotating System
2.1. Lagrangian Solution for the Rotating Frame of Reference
- The rotating frame of reference is a frame that rotates around a spin axis (fixed for simplicity) with a given angular velocity. A rotating frame of reference is usually characterized by three inertial forces: the centrifugal force, the Coriolis force, and for a non-uniformly rotating frame of references, the Euler force [14]. The rotating frame of reference can be described through the general case of a rigid body in rotational motion and a fixed frame [15]. It is considered the distance from the spin axis to the final position of a point P that according to the fixed frame of reference is the radius vector named rf (which will be considered as our generalized coordinate in the rotating system for the Lagrangian solution), while some position of the same point according to the rotating frame of reference is named r, and
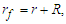 | (1) |
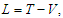 | (2) |
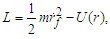 | (3) |
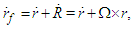 | (4) |
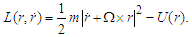 | (5) |
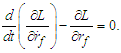 | (6) |
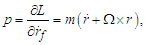 | (7) |
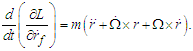 | (8) |
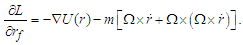 | (9) |
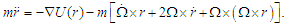 | (10) |
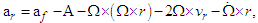 | (11) |
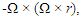 and
and 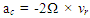 is the Coriolis acceleration. When the final velocity vf is equivalent to the Coriolis velocity vc, yields:
is the Coriolis acceleration. When the final velocity vf is equivalent to the Coriolis velocity vc, yields: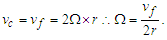 | (12) |
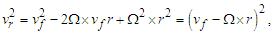 | (13) |
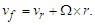 | (14) |
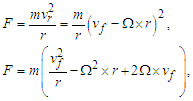 | (15) |
2.2. Total Force in the Rotating Frame of Reference
- As usual, the total energy in a rotating system is given by:
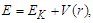 | (16) |
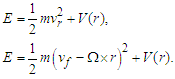 | (17) |
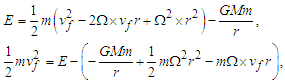 | (18) |
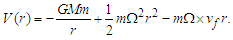 | (19) |
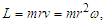 | (20) |
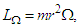 | (21) |
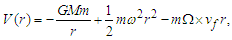 | (22) |
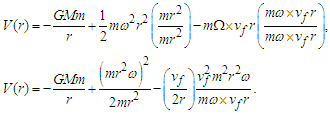 | (23) |
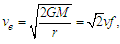 | (24) |
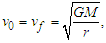 | (25) |
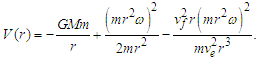 | (26) |
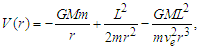 | (27) |
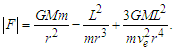 | (28) |
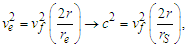 | (29) |
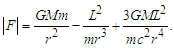 | (30) |
3. Apsidal Precession in the Rotating Frame of Reference
- Considering a body with rest mass m in a circular orbit at a distance r from the spin axis of a rotating system, precession results from the angular velocity of rotation and the angular velocity produced by the torque [8]. Then, the orbiting body will undergo precession expressed by the angular velocity of precession ωφ as described for a rotating gyroscope of radius r [25], with some equivalencies defined as:
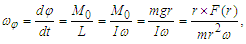 | (31) |
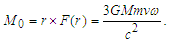 | (32) |
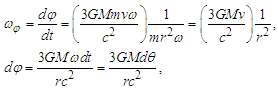 | (33) |
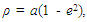 where a is the semi-major axis and e is the eccentricity. When the body moves in one revolution (θ = 2π radians), becomes:
where a is the semi-major axis and e is the eccentricity. When the body moves in one revolution (θ = 2π radians), becomes: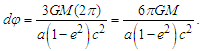 | (34) |
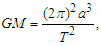 | (35) |
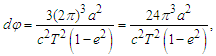 | (36) |
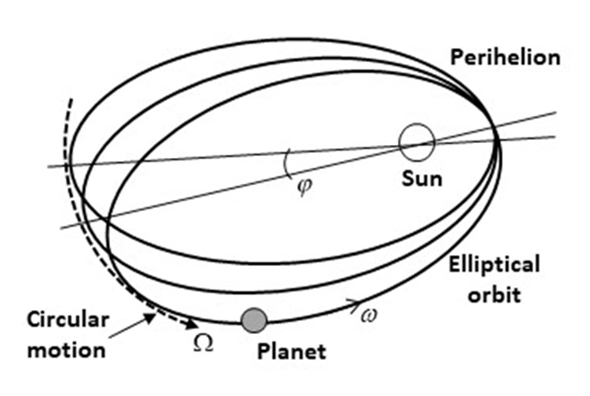 | Figure 1. Precession of Mercury’s perihelion in a rotating frame of reference with angular velocity Ω |
4. Axial Precession in the Relativistic Solution
- Considering that the entire disk of the Solar System could be rotating like a rigid body, the effect of that motion should be perceived from the Earth as a change in linear position with respect to the considered “fixed” stars, noting that these would have an apparent periodic circular motion [9,10]. From the third term of (30) for a rotating system, reducing common terms, becomes:
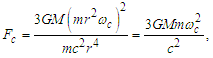 | (37) |
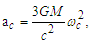 | (38) |
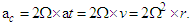 | (39) |
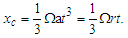 | (40) |
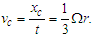 | (41) |
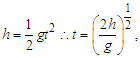 | (42) |
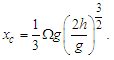 | (43) |
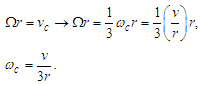 | (44) |
 | (45) |
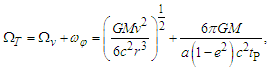 | (46) |
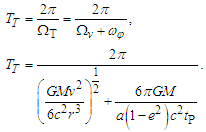 | (47) |
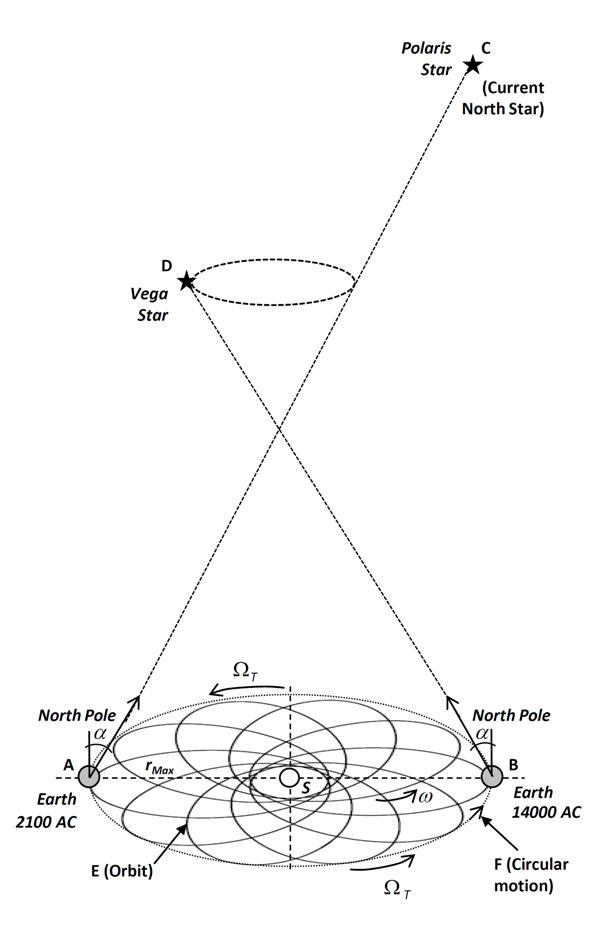 | Figure 2. Entire disk of the Solar System scheme rotating like a rigid body for the Earth’s orbit. Earth periodically would be changing its position with respect to the considered “fixed” stars |
5. Rotational Velocities Solution in Spiral Galaxies
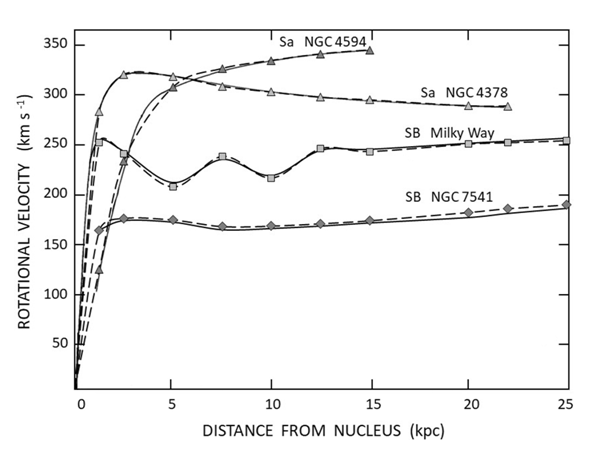
- We revisit the equation that describes the rotational velocity of stars in spiral galaxies based on the general relativity solution [11]. And based on the Kerr metric, dynamics and geometry of barred spiral galaxies [12] are explained. In particular, we show examples of the calculated rotation curves of unbarred spiral galaxies NGC 4378 and NGC 4594, and barred spiral galaxies Milky Way and NGC 7541, comparing our calculations with the observations, finding a good approximation.
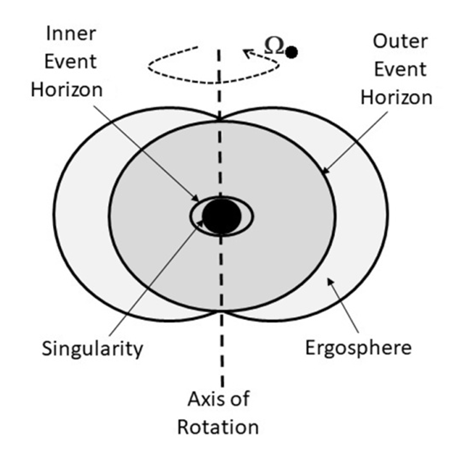
5.1. Kerr Metric in the Barred Spiral Galaxies
- The Kerr metric [29] is an exact solution of the vacuum Einstein equations that generalizes to a rotating uncharged black hole with angular velocity
 different of zero and of massive resting mass
different of zero and of massive resting mass  of the Schwarzschild metric [24]. In Kerr’s original paper, he presented the metric in the following form
of the Schwarzschild metric [24]. In Kerr’s original paper, he presented the metric in the following form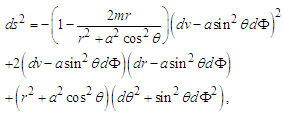 | (48) |
 | Figure 3. Kerr metric of a rotating black hole |
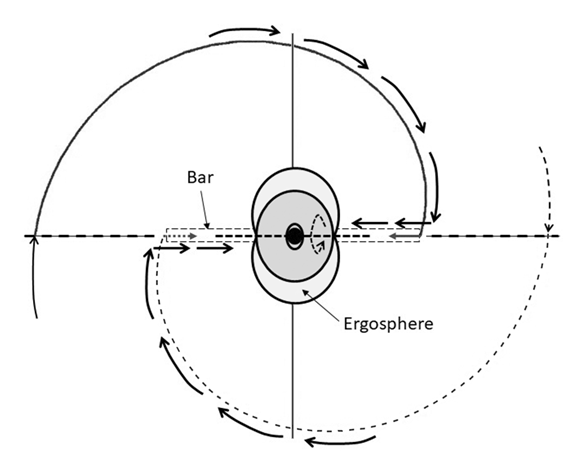 | Figure 4. The dynamics around the Kerr metric of a rotating black hole, and the forming of the bar of a barred spiral galaxy |
5.2. Rotational Velocity for Spiral Galaxies
- Considering Eq. (37) from the relativistic solution for the force FC, in the same way as with the equation for classical mechanics scenario, we equate it to the centrifugal force Fc [11], obtaining:
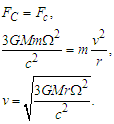 | (49) |
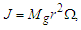 | (50) |
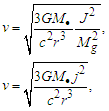 | (51) |
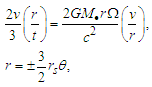 | (52) |
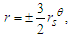 | (53) |
5.3. Comparison between Calculated and Observed Rotational Velocities in Spiral Galaxies
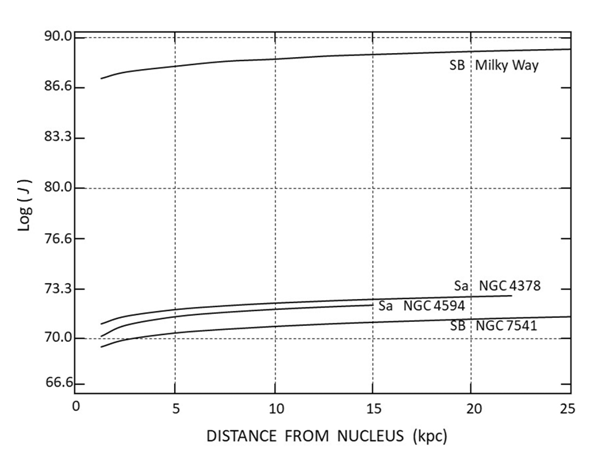
- The rotational velocity of some unbarred and barred spiral galaxies are calculated by applying (51). In particular, considering as an example the known rotation curves of the spiral Sa galaxies: NGC 4378 and NGC 4594, and spiral SB galaxies: Milky Way and, NGC 7541. Thus, having the known values for each of these four spiral galaxies [32-38], the results are tabulated in Table 1 (Rotational velocities) for each galaxy. It is observed that the nucleus masses of barred spiral galaxies are larger than the nucleus masses of unbarred spiral galaxies. The rotation curves are plotted in Figure 5, which shows the calculated results for these galaxies. The observed rotation curves of these galaxies [39,40] are superimposed on the calculated rotation curves. Then, the solid lines in Figure 5 show the rotation curves obtained from the observations. And the rotation curves calculated with (51) are shown as dashed lines, finding a good approximation between the calculated rotation curves and the known rotation curves of these spiral galaxies. The respective angular momentum along the different distances from the nucleus for these spiral galaxies are plotted in Figure 6. It is shown the same almost linear pattern of angular momentum for all these spiral galaxies. On the other hand, the Oort constants [41] have not been considered in this work, since such constants are empirically derived parameters that particularly characterize the local rotational properties of the Milky Way.
6. Conclusions
- This work aims to summarize the previous works that together describe the theory in which the movement of some circular or disk cosmological systems, such as the entire disk of the Solar System and spiral galaxies, corresponds to the dynamics like a rigid body in rotational motion. It has been found that both the Lagrangian solution and the relativistic solution consider all the energies and forces involved in the rotating systems in the three-dimensional framework. In this way, most of the equations on this work are derived from Eq. (1), which is the formula of the system for the rigid body in rotational motion. This shows that the relativistic solution for the total force considers the dynamics of a rotating system like a rigid body in rotational motion. There are derived the respective equations to explain the apsidal precession of the planets, the Earth’s axial precession and the rotation curves of some spiral galaxies, all of them due to the effect of rotating systems like a rigid body in rotational motion. A good approximation between the calculated and the observations for each of these cases has been found. Thus, this theory unifies classical mechanics (through Lagrangian mechanics) with the solution of general relativity in the three-dimensional framework. Also, it unifies all these rotational behaviour of these circular or disk cosmological systems in the same concept of the rigid body in rotational motion. Then, (51) describes the rotational velocity of some spiral galaxies based on this relativistic solution. We present preliminarily examples of the rotation curves of unbarred spiral galaxies: NGC 4378 and NGC 4594, and barred spiral galaxies: Milky Way and, NGC 7541. Comparing our calculations with the observations we find a good approximation. Furthermore, the existence of barred spiral galaxies could be a confirmation of the Kerr metric. It is shown that the respective angular momentum for these spiral galaxies has the same almost linear pattern along the different distances from their respective nucleus. One of the significances of this result based on the general relativity solution is that it is possible to fit the known rotation curves of the spiral galaxies without any need of introducing dark matter at all. The next step in proving the galaxy dynamics on the general relativity solution is to make more detailed observations of their angular momentum to confirm if the way in which spiral galaxies rotate is mainly according to rigidly rotating and long-lived patterns, as steady spirals.
ACKNOWLEDGEMENTS
- The author would like to thank Professor Sergio S. Cornejo for its review and comments for this work.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML