-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Astronomy
p-ISSN: 2169-8848 e-ISSN: 2169-8856
2021; 10(1): 13-21
doi:10.5923/j.astronomy.20211001.03
Received: Feb. 11, 2021; Accepted: Apr. 2, 2021; Published: Apr. 15, 2021

Quantum Black Hole Properties and Gravity Effect
C. Achoundong1, C. Kenfack-Sadem1, A. Fomethe2, M. F. C. Fobasso1, A. J. Fotue1, L. C. Fai1
1Laboratory of Condensed Matter-Electronics and Signal Processing (LAMACET), Department of Physics, University of Dschang, Dschang, Cameroon
2UR de Mécanique et de Modélisation des Systèmes Physiques (UR-2MSP), Faculté des Sciences, Université de Dschang, Dschang, Cameroun
Correspondence to: C. Achoundong, Laboratory of Condensed Matter-Electronics and Signal Processing (LAMACET), Department of Physics, University of Dschang, Dschang, Cameroon.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, we investigate some thermodynamics properties of quantum Black Hole. The Black Hole of Reissner-Nordstrom model with a self-gravitating charged pure vacuum shell as a source is studied using Schrödinger equation. We show that the density energy strongly influences the horizon radius of the black hole. It is shown that the gravity has no effect for certain values of the mass of quantum black hole. Moreover, the probability density shows that Black Hole stabilises itself when the radius increases. We show that the quantum Black Hole loses information when the event horizon increases. We show the evidence that quantum black Hole emit information. It is seen that the heat capacity increases with temperature and follow the Dulong and Petit Low. We observed that the Quantum black Hole system loses a certain amount of energy.
Keywords: Quantum Black hole, Gravity, Phase transition
Cite this paper: C. Achoundong, C. Kenfack-Sadem, A. Fomethe, M. F. C. Fobasso, A. J. Fotue, L. C. Fai, Quantum Black Hole Properties and Gravity Effect, International Journal of Astronomy, Vol. 10 No. 1, 2021, pp. 13-21. doi: 10.5923/j.astronomy.20211001.03.
Article Outline
1. Introduction
- Nowadays, advanced researches in physics of high energy have attracted many scientists, particularly the fascinating science of Black Hole (BH) [1,2]. Thus, many connections have been made between astronomy and certain theories of physics in order to better understand the physics of black holes [3], and this is how astrophysics was born [4,5]. In principle, astrophysicists create and evolve physical models and theories to reproduce and predict observations. The tools used are of great variety and include analytical models and numerical analysis. These models lead us to study several aspects such as stellar dynamics and the evolution of stars, the great structures of matter in the universe, the origin of cosmic rays, general relativity, cosmology, which serves as a basis for the astrophysics of black holes and the study of gravitational waves. A variety of theoretical arguments indicate that black holes can be studied as classical or quantum object. Classically, black hole (BH) is a region of space time exhibiting strong gravitational effect where particles and light cannot escape once it's swallowed up. BHs can be considered as a perfect absorbers [6]. A BH is not really black, because it reflects no light [7,8]. They are described by several parameters such as their mass, angular momentum and charge. In views of such issues, there are four basics theoretical kinds of black holes solutions from Einstein equation depending on the metric which is the key to understand the physics of black hole [9]. Nowadays, classical General Relativity still provides successful description of gravity. However, it may be reasonable to consider gravitational effects in BH’s study. We know that quantum mechanics plays a vital role in the behaviour of the matter fields. There appears the problem of defining a consistent scheme in which the space-time metric is treated classically but is coupled to the matter fields which are treated quantum mechanically [10]. Thereby come the origin of quantum black hole (QBH) [11].Concerning the quantum black holes also called micro black holes, much work has been done using a fixed background during the emission process first pointed out by Hawking [12]. In 1974 he discovered that BH should emit a black body radiation with the temperature depending on their parameters. This idea is seen as paradox for many scientists because in classical level, BH is considered as an object which cannot emit any radiation [13]. The basic idea is that, due to natural interactions and fluctuations in the vacuum, the matter will be created in the form of an electron and anti-electron. When this occurs near the event horizon, one particle will be ejected away from the BH, while the other will fall into the gravitational well [14]. In 1984, Gerad’t Hooft [15] suppose that BH should be subject to the same roles of quantum mechanics as ordinary elementary particles, he concludes that they can radiate as a black bodies with a certain temperature and the energy density can easily be drawn. In 1996, Marcello barreira et al [16] point out quantum gravitational effects on BH radiation, using loop quantum gravity. He derived the emission spectra by using loop quantum gravity and showed that the quantum properties of geometry affect the radiation considerably. Hawking radiation from BH is nowadays one of the most remarkable effect which can be justify using a combination of quantum mechanics and general relativity [17,18,19].In this paper we used classical and quantum methods to show that QBH stores energy and emits information as was respected by literatures [20,21,22]. Intense researches [23,24,25] as carried out in order to determine the thermodynamics properties of BH. In 2017 Mahamat Saleh et al [26] derived the energy and thermodynamics in schwarzchild black hole by considering quantum fluctuation, The results show that due to the quantum fluctuations in the background of the Schwarzschild BH, all the energies increase and Einstein energy differs from Møller’s one. Moreover, when increasing the quantum correction factor, the difference between Einstein and Møller energies, the Unruh-Verlinde temperature and the heat capacity of the black hole increase while the Hawking temperature remains unchanged. Berezin [27,28] considered that the temperature of the Reissner nordstrom BH grows when its mass decrease. He investigated a model of BH interacting with the background metric. In addition, He found that as the mass of the black hole decreased, the area of the event of horizon go down, thus violating the law that, classically, the area cannot decrease. So far, however, the gravity effect has not yet been treated in the number of papers. In this paper, a Reissner Nordstrom BH surrounded with the gravity effect is considered to investigate the thermodynamic properties and the stability of the black hole. The paper is organized as follows. In section 2, we begin by outlining the model of BH interacting with gravity effect. We also quantify the system and then calculate thermodynamics parameters. Section 3 is devoted to results. We end with conclusion.
2. Model and Calculations
2.1. Hamiltonian of the System
- There exist many ways to analyze the information in BH. One of the method is to employ classical general relativity [29,30,31,32]. We first investigate the Hamiltonian of the system. The general spherical symmetric metric can be represented as:
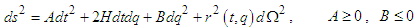 | (1) |
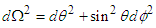 is the line interval of the unit sphere.
is the line interval of the unit sphere.  and
and 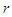 are functions of
are functions of 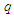 and
and 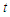 only. We consider now the condition of orthogonality which requires that:
only. We consider now the condition of orthogonality which requires that: 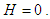 | (2) |
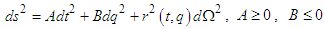 | (3) |
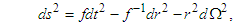 | (4) |
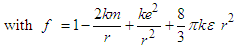 | (5) |
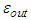 is the density energy of external space and the mass of the BH can be written from (2) in terms of the areal coordinate
is the density energy of external space and the mass of the BH can be written from (2) in terms of the areal coordinate 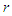 as:
as: 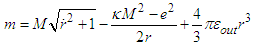 | (6) |
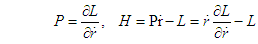 | (7) |
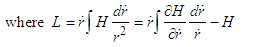 | (8) |
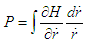 | (9) |
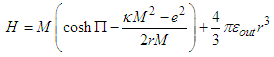 | (10) |
2.2. Schrödinger Equation and Probability Density
- The stationary equation of Schrödinger is given by:
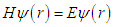 . Using the commutation relation
. Using the commutation relation 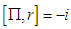 and
and 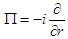 , we obtain the Schrödinger equation:
, we obtain the Schrödinger equation: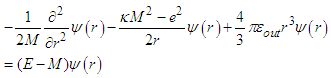 | (11) |
2.3. Horizon Radius and Area of BH
- Let consider the dynamics invariant of Reissner Nordstrom BH:
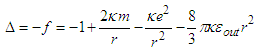 Let’s determine the solutions of:
Let’s determine the solutions of: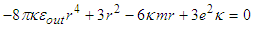 | (12) |
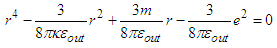 | (13) |
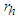 . However, the best way to extract thermodynamic information about the BHs is given by horizon radius. By taking into consideration the approximation
. However, the best way to extract thermodynamic information about the BHs is given by horizon radius. By taking into consideration the approximation 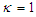 , and
, and 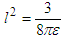 we can rewrite Eq. (13) in the form:
we can rewrite Eq. (13) in the form: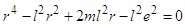 | (14) |
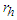 and
and 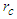 representing respectively the horizon radius and cosmologic radius are given by:
representing respectively the horizon radius and cosmologic radius are given by: | (15) |
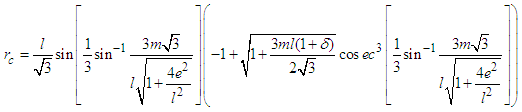 | (16) |
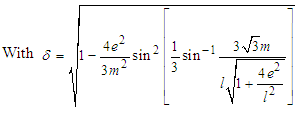 | (17) |
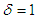 , the
, the  expansion as a function of
expansion as a function of 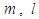 and
and 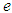 give:
give: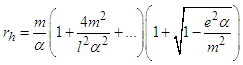 | (18a) |
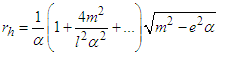 | (18b) |
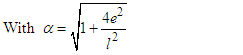 | (19) |
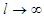 ,
, 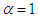 and
and 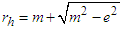 , we have the limiting case which coincides with the result that we know (the Reissner Nordstrom Black Hole):
, we have the limiting case which coincides with the result that we know (the Reissner Nordstrom Black Hole): 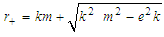 and the Schwarzschild BH for
and the Schwarzschild BH for 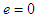 .These results are obtaining especially when we take into account the self-gravitational interaction, the background space time as dynamical and the energy as conservation. There are a number of different ways in which thermodynamic ideas can be introduced into black hole physics, the simplest approach is to consider the black holes as a spherical quantum object allowed to radiate. However, when quantum mechanical effect is taking into account, it supposes that black hole emit thermal radiation, so we can now investigated on thermodynamic properties of black holes.According to the second law of thermodynamics, the event horizon always increases.
.These results are obtaining especially when we take into account the self-gravitational interaction, the background space time as dynamical and the energy as conservation. There are a number of different ways in which thermodynamic ideas can be introduced into black hole physics, the simplest approach is to consider the black holes as a spherical quantum object allowed to radiate. However, when quantum mechanical effect is taking into account, it supposes that black hole emit thermal radiation, so we can now investigated on thermodynamic properties of black holes.According to the second law of thermodynamics, the event horizon always increases.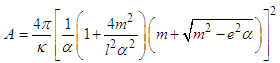 | (20) |
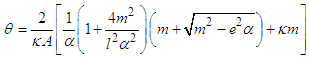 | (21) |
3. Numericals Results
- We will display here the curve for the horizon radius and area of the BHs all as functions of mass. We also plot the diagram of density probability and heat capacity.Figure 1 shows the graph of horizon radius as function of the mass of BH for different values of the vacuum energy density. It is observed that the horizon radius increases with the mass and exhibits parabolic shape, which means that the gravitational potential gradually increases the horizon radius. Increases faster for large masses than small masses. But when the parameter
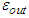 become smaller, the shape of our curve become linear. This means that black holes change in size for different value of density energy. Therefore, this behaviour has important consequences on the shape of black hole. We also see that for
become smaller, the shape of our curve become linear. This means that black holes change in size for different value of density energy. Therefore, this behaviour has important consequences on the shape of black hole. We also see that for 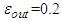 and
and 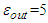 the curve is linear and not
the curve is linear and not 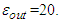 Moreover we also observe two points of singularities where density energy didn’t have effect on the curve.
Moreover we also observe two points of singularities where density energy didn’t have effect on the curve. 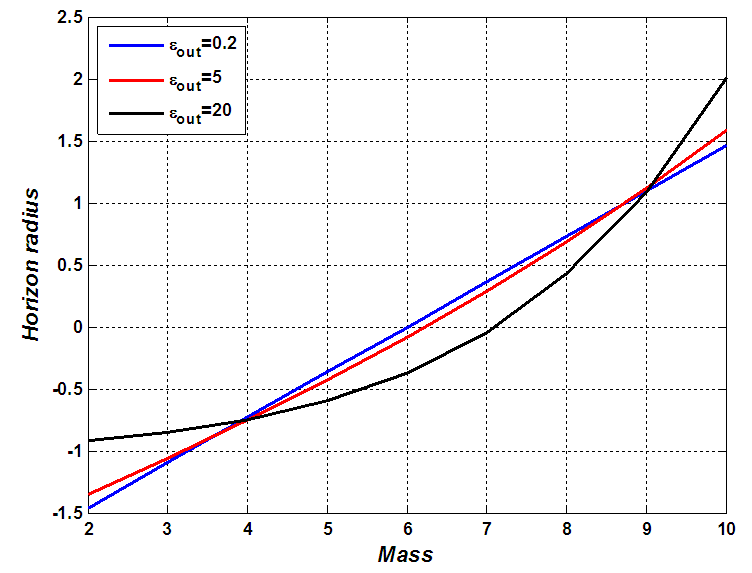 | Figure 1. Variation of horizon radius 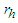 with mass with mass 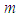 |
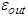 . We observe that the area of thee RN black hole increases with mass. We observe also that the area has several behaviour when we vary the vacuum energy density. While increasing the mass, we found that the area of a BH is not sensitive to the vacuum energy. Indeed, Berezin [37] proved that the area of a BH cannot decrease. This is confirmed in the present work and going further, by adding the gravitational term, we do not break down the theory. This also confirms the second law of thermodynamics for BHs problems. If the mass of BH increases then this means that its surface area adds its volume too. And since the area of a BH is linked with the entropy of a system, we can say that by increasing the area we increase also the entropy knowing the formula
. We observe that the area of thee RN black hole increases with mass. We observe also that the area has several behaviour when we vary the vacuum energy density. While increasing the mass, we found that the area of a BH is not sensitive to the vacuum energy. Indeed, Berezin [37] proved that the area of a BH cannot decrease. This is confirmed in the present work and going further, by adding the gravitational term, we do not break down the theory. This also confirms the second law of thermodynamics for BHs problems. If the mass of BH increases then this means that its surface area adds its volume too. And since the area of a BH is linked with the entropy of a system, we can say that by increasing the area we increase also the entropy knowing the formula 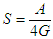 . These results have been obtained by [38] when they studied the spectroscopy and thermodynamics of MSW BHs. The volume enclosed within a given area is maximized for a spherical surface; this is the reason soap bubbles are spherical. For BHs, surface area corresponds to entropy, so from thermodynamically considerations, we would expect that spherical BHs would maximize entropy [39].
. These results have been obtained by [38] when they studied the spectroscopy and thermodynamics of MSW BHs. The volume enclosed within a given area is maximized for a spherical surface; this is the reason soap bubbles are spherical. For BHs, surface area corresponds to entropy, so from thermodynamically considerations, we would expect that spherical BHs would maximize entropy [39].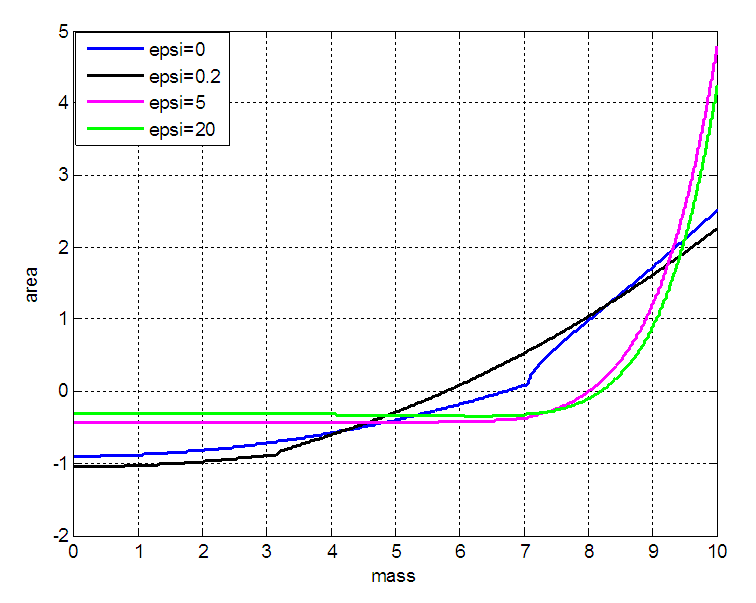 | Figure 2. Variation of area 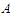 of BH with mass of BH with mass 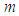 for different values of vacuum energy density for different values of vacuum energy density 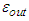 |
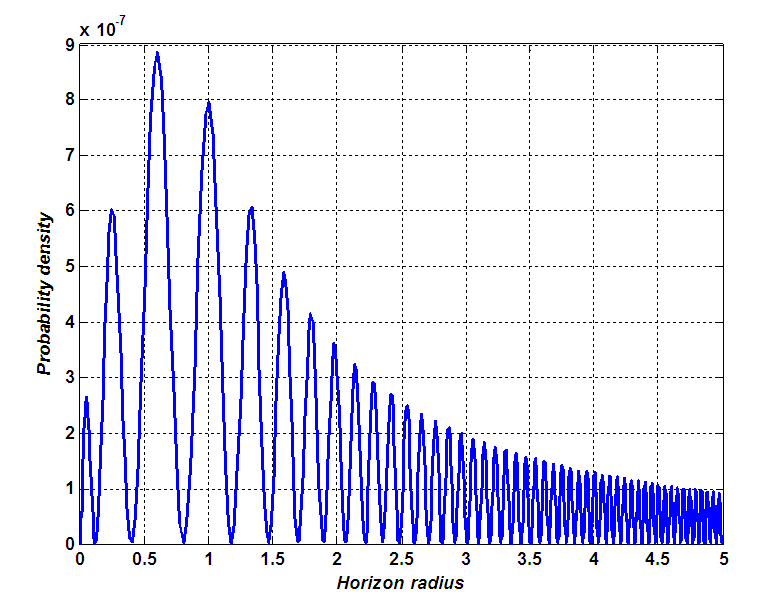 | Figure 3. Probability density 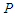 of a BH as function of horizon radius of a BH as function of horizon radius 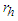 with the presence of gravity with the presence of gravity |
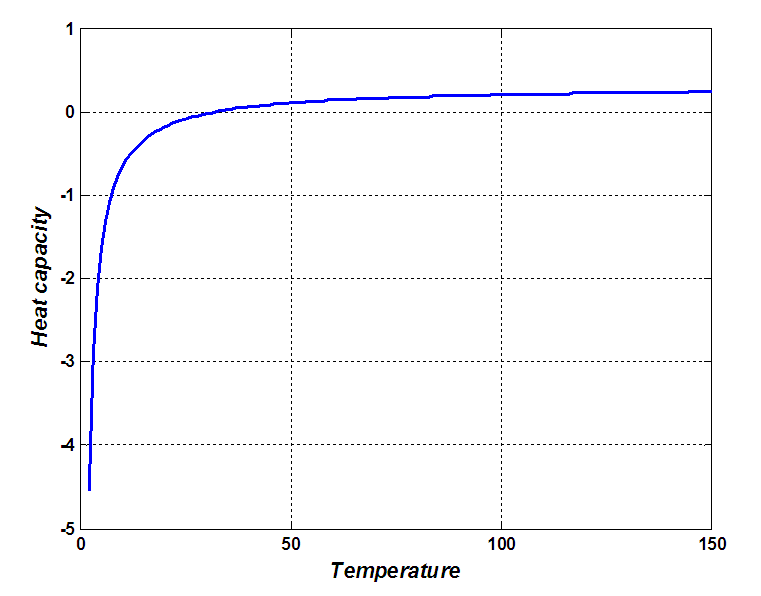 | Figure 4. Heat capacity 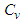 as function of temperature as function of temperature 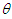 of a BH of a BH |
4. Conclusions
- They are several alternative approaches to study information in black holes. In this paper, based on the previous work of Berezin and some recent literature, we have discussed the gravitational effect on quantum black holes of Reissner Nordstrom especially on the thermodynamic properties. First of all, we investigate the classical equation of motion which helps to quantize the system. From Schrödinger equation we see that when the horizon radius of a BH has a high value, its amplitude reduces and tends to stabilize the system which loses energy. We determine the thermodynamic quantities from dynamic invariant, such as the temperature, heat capacity, entropy. The temperature shows that the mass of BH decreases when the temperature increases. We show that the heat capacity of the system is a function of temperature and follow the Dulong and petit law. We observe that for the high value of temperature, the heat capacity tend to be positive, attain a saturate value which means that the system does not communicate any more with its surrounding at resonance.
Appendices
- Appendix ATo solve the polynomials in one variable we shall consider how to compute and how to represent the zero of a general polynomial of degree d in one variable r
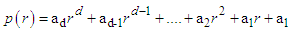 If the degree d is four or less, then the root are functions of the coefficients which can be express in terms of radicals. As it is shown in [42] it is easy to obtain those roots with Maple or Mathematica Software.Appendix BTo determine the Hamiltonian of equation (10), we proceed as followsFrom the equation of dynamics of BH given by
If the degree d is four or less, then the root are functions of the coefficients which can be express in terms of radicals. As it is shown in [42] it is easy to obtain those roots with Maple or Mathematica Software.Appendix BTo determine the Hamiltonian of equation (10), we proceed as followsFrom the equation of dynamics of BH given by 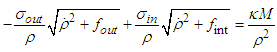 | (A1) |
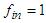 in the Minkovsky’s space and
in the Minkovsky’s space and 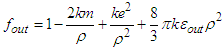 .We replace
.We replace 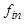 and
and 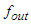 into equation (1) and we obtain:
into equation (1) and we obtain: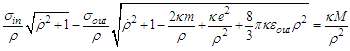 | (A2) |
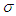 represent extrinsic curvature tensor
represent extrinsic curvature tensor 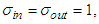 Relation (2) implies that
Relation (2) implies that 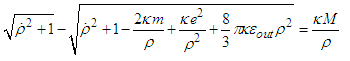 | (A3) |
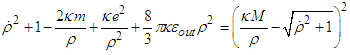 | (A4) |
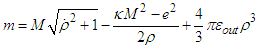 | (A5) |
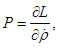 The equation of motion involving Hamiltonian and Lagrangian are:
The equation of motion involving Hamiltonian and Lagrangian are: 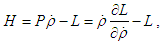 and
and 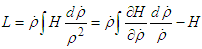 By evaluating each terms, we obtain relations
By evaluating each terms, we obtain relations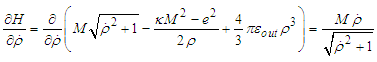 | (A6) |
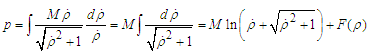 | (A7) |
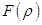 is an arbitrary function. The choice of this function does not affect the Lagrangian equations of motion. Therefore the Lagrangian is written as
is an arbitrary function. The choice of this function does not affect the Lagrangian equations of motion. Therefore the Lagrangian is written as 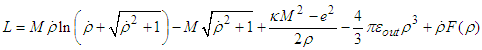 Suppose that
Suppose that 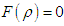 (A7) becomes
(A7) becomes 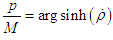 Then, the derivative of areal coordinate is
Then, the derivative of areal coordinate is 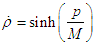 | (A8) |
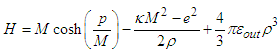 | (A9) |
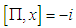 and
and 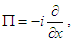 If
If 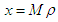 then
then 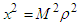 ,
,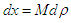 then
then 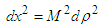 The Hamiltonian becomes:
The Hamiltonian becomes: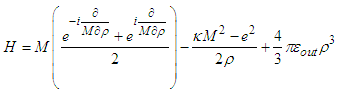 | (A10) |
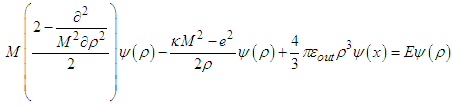 | (A11) |
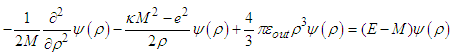
Note
- 1. This law was formulated in 1819 by Pierre Louis DuLong and Alexis Therese Petit.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML