Adrián G. Cornejo
Electronics and Communications Engineering from Universidad Iberoamericana, Santa Rosa 719, CP, Querétaro, Mexico
Correspondence to: Adrián G. Cornejo , Electronics and Communications Engineering from Universidad Iberoamericana, Santa Rosa 719, CP, Querétaro, Mexico.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This work describes the hypothesis where the explanation of the Earth’s axial precession can be based on the General Theory of Relativity solution. In this solution, the entire Solar System disk would rotate like a solid (or rigid) body, so that the Earth changes its position with respect to the “fixed” stars. On this assumption, we define the equation that describes the period of Earth’s axial precession based on the relativistic solution and comparing our estimates with the observations, finding a good approximation between the estimated period of the Earth’s axial precession and the observations.
Keywords:
Solar system: General, Planet-disk interactions, General Theory of Relativity
Cite this paper: Adrián G. Cornejo , Axial Precession in the General Theory of Relativity Solution, International Journal of Astronomy, Vol. 10 No. 1, 2021, pp. 1-5. doi: 10.5923/j.astronomy.20211001.01.
1. Introduction
Axial precession, also called precession of the equinoxes, is one of the Earth’s movements, currently considered the circular movement of the rotational axis, whereby the axis slowly traces out an imaginary cone with respect to the “fixed” stars.Thus, what is seen is that Earth’s axis rotates completely around 360° in a period of about 25,771.5 years (called Platonic year) [1], which implies an axial precession of about 0.0139689° per year. During such a period, the visible positions of stars as measured in the equatorial coordinate system will slowly change. The projection onto the sky of Earth’s axis of rotation results in two notable points at opposite directions: the North and South celestial poles. Over this cycle the Earth’s North axial pole apparently moves from where it is appointing now (within 1° of Polaris star) in a circle about the ecliptic pole, with an angular radius (α) in average of 23.45°. Currently, there is a classical solution, but not yet fully proven and confirmed to date, which attempts to explain the axial precession, considering that this precession is caused by the gravitational influence of the Sun and the Moon acting on Earth’s equatorial bulge. Then, considering that the precession of Earth’s equinoxes is due to the Sun and Moon torques [2]. To a much lesser extent, the planets would exert influence as well [3].However, the fact that the planets also influence on the axial precession, would indicate that this precession should not be as regular as it is observed, since each planet changes its position within the Solar System at a different rate and these could not exert a regular influence on Earth throughout the Platonic period. Furthermore, it is known that all the planets precess due to the apsidal precession, and Earth’s orbit motion by the apsidal precession is not currently considered in this classical solution for axial precession, which should cause a difference in the calculated axial precession when Earth’s apsidal precession is considered. In addition, it is considered that Newtonian theory of gravity, that is the theory on which the current explanation of axial precession is based, presents limitations typical of this type of classical theory, mainly regarding to rotating systems, as that this theory does not consider all the energies involved in a rotating system, as Lagrangian mechanics and the General Theory of Relativity do [4].Moreover, this classical solution does not directly consider the General Theory of Relativity (GTR) [5], which also includes the Newtonian theory of gravity, as well as considers the distortion of space-time, the dynamics of the expansion of the universe and all the energies, kinetics and potentials, involved in the dynamics of the rotating systems, and has been shown to be a predictive theory that has been able to coherently describe the dynamics and kinematic and dynamic behaviour of most celestial bodies in space-time. Thus, in this solution we will give possible explanations that solve those inconsistencies, based on the General Theory of Relativity solution, which also considers the apsidal precession in the solution. Then, we found that this axial movement can be estimated from the total force equation for a rotational gravitational system solution derived from the General Theory of Relativity, being composed by the sum of the Newtonian force of gravity, the centrifugal force and the force related to the Coriolis force. Then, this solution is different to the classical solution of the Newtonian force in the third term, since it includes the force with the inverse of the distance to the fourth power.The aim of this work is to describe the hypothesis where the explanation of the axial precession can be based on the General Theory of Relativity solution. In this solution, entire Solar System disk would rotate like a solid (or rigid) body, so that Earth would periodically change its position with respect to the “fixed” stars (Fig. 1).Thus, we define the equation that describes the period of axial precession based on the relativistic solution and comparing our estimates with the observations, finding a good approximation between the estimated period of the Earth’s axial precession and the observations.
2. General Theory of Relativity Solution for the Total Force
A relativistic solution for the angular movement of the celestial bodies in a rotational system can be determined from a study of the solutions of Einstein’s equations following the standard procedure [6,7]. Thus, the total force for a rotating system is given as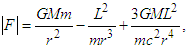 | (1) |
where r is a position vector and L is the orbital angular momentum of the rest mass m, given by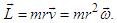 | (2) |
The first term in Eq. (1) represents the Newtonian gravitational force, which is described by the inverse-square law. This is the case of Newton equation [8] that describes the orbital motion of planets around the Sun. The second term represents the centrifugal force in the circular motion. The third term is related to the Coriolis force, which includes the inverse of the distance to the fourth power, which is derived from the GTR.
3. Apsidal Precession in the Rotating Reference Frame
In a rotating reference frame, precession results from the angular velocity of rotation and the angular velocity produced by the torque [4], which matching with the General Theory of Relativity solution. Let us consider a body with rest mass m in circular orbit at a distance r from the axis of rotation. In such a framework, the orbiting body will undergo precession expressed by the angular velocity of precession ωφ as described for a rotating gyroscope of radius r [9], with some equivalencies defined as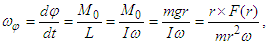 | (3) |
where dφ is the differential of the precession angle, dt is the time differential, M0 is the modulus of angular momentum, I is the moment of inertia of a ring of radius r, ω is the angular velocity around the axis of rotation and g is the gravitational acceleration. When a solid body rotates around its spin axis under an external force (given by F(r) = m∙g), the moment of the external forces is not null, and the angular momentum is non-conservative (L ≠ 0). Thus, the angular momentum changes direction with precession as an additional circular motion. Taking into account the third term of Eq. (1) and taking the rotational velocity ω × r of a body in circular motion, the angular momentum of inertia is written as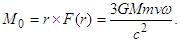 | (4) |
The angular velocity of precession for a body revolving around a central point can be estimated by substituting Eq. (4) into Eq. (3), giving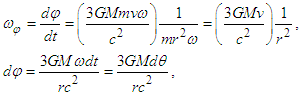 | (5) |
where dθ is the differential of the radial angle covered by the rotation of the body in the rotational framework. Extending Eq. (5) to celestial mechanics, consider Kepler’s geometry with a planet in elliptical orbit around the Sun as the focus. In the ellipse we have that ρ = a(1 - e2), where a is the semi-major axis and e is the eccentricity. When the eccentricity tends to zero, parameter ρ tends to the radius r of a circle. While the body moves in one revolution (θ = 2π radians), the precession angle dφ for elliptical motion can be written as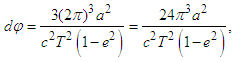 | (6) |
giving the same relativistic equation that is used to estimate the advance of Mercury’s perihelion [10]. As known, by substituting the known data for Mercury [11] into Eq. (6), the perihelion advance of Mercury can be estimated for approximately 43.013” arc per century. It is known today that all planets precess, regardless of their distance from the Sun, and this equivalence can be applied to determine the apsidal precession of all other planets in the Solar System, giving the same results as the observations for each respective apsidal precession.
4. Axial Precession in the Relativistic Solution
In the scenario where the entire Solar System disk is rotating like a solid body, the effect of that motion should be perceived from the Earth as a change in linear position with respect to the “fixed” stars, noting that these would have an apparent periodic circular motion [12]. Taking into account the third term of Eq. (1) for a rotational system [13], we can reduce the common terms, giving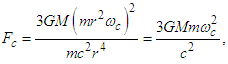 | (7) |
and for the acceleration, we can write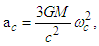 | (8) |
where ac is related to the Coriolis acceleration, also having the following equivalences: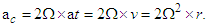 | (9) |
Integrating Eq. (9) two times with respect to time, we obtain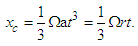 | (10) |
In the case of the free fall of a body, xc is the displacement in the opposite direction to the Earth’s rotation, and its velocity is given as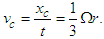 | (11) |
The time to reach the ground is given by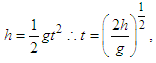 | (12) |
where h is the height and g is the gravitational acceleration. Then, substituting Eq. (12) into Eq. (10), the final displacement is given as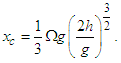 | (13) |
To get an idea of the magnitude of this displacement xc, let us consider an object at the equator free falling from a height of 100 meters. Substituting these values into Eq. (13) gives a total displacement of about 2.2 cm. This amount is small compared to the 100-meter drop, but it is certainly measurable. Furthermore, from Eq. (11) and with the equivalence Ω = v/r for circular motion, we obtain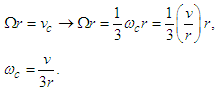 | (14) |
With this condition, from Eqs. (8), (9) and (14) we can write the equation equivalent to the case of a rotating disk in the plane of rotation as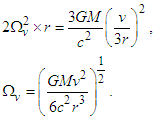 | (15) |
Since apsidal precession in a planet is that its orbit has a periodic advance, it is necessary to include this movement of Earth’s orbit. From the General Theory of Relativity solution, the apsidal precession is given by Eq. (6). Thus, the total angular frequency ΩT of the system is obtained by adding the apsidal precession from Eq. (6) for a rotating and orbiting body, giving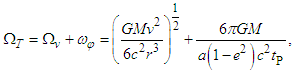 | (16) |
where tP is the time in seconds of a sidereal year. Then, for one revolution (2π radians), the total period is given by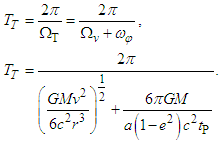 | (17) |
Substituting the Earth-Sun system data [14] into Eq. (17) for the maximum distance rMax (during the aphelion), and the related minimum orbital velocity v, total angular frequency equals 7.72554 × 10−12 radians per second (50.2881” arc per year, or 0.0139689° per year). For one revolution (2π radians), total period in the case of the Earth equals 8.133 × 1011 seconds (25,771.5 years), which is according to the observed period of Earth’s axial precession.Thus, a consequence of the axial precession is a changing pole star. Currently, Polaris star (at a distance from Earth of about 323 – 433 ly) is extremely well-situated to mark the position of the North celestial pole. According to the observations, in the year 2100 AC, Earth’s North Pole will appoint at only 0.5° of Polaris star. Vega star (at a distance from Earth of about 25.04 ± 0.07 ly) in the constellation Lyra is often touted as the best North star due to its brightness. It fulfilled that role around 12000 BC and will do so again around the year 14000 AC. However, it never comes closer than 5° to the North Pole.According to the Fig. 1, we can interpret that about the year 2100 AC (point A), Earth’s North Pole will be appointing near of Polaris star (point C); and later, when planet travels out by half period of the Platonic year to the opposite side (point B) by such a circular motion, then Earth’s North Pole will appoint near of Vega star (point D) in the year 14000 AC, changing the Earth its position within the Solar System and also maintaining in average the same angular radius (α in Fig. 1) with respect to the ecliptic, then changing its linear reference with respect to the “fixed” stars, and resulting in the effect of the axial precession, matching with the known observations and predictions.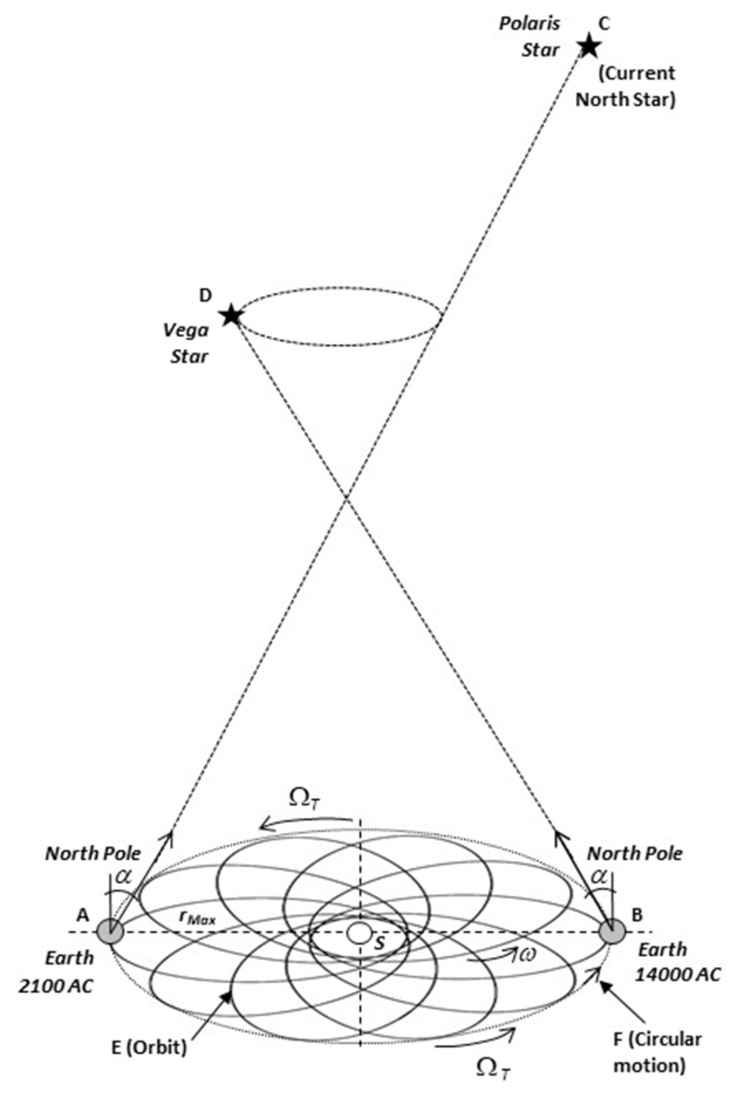 | Figure 1. Entire Solar System disk scheme rotating like a solid (or rigid) body for the Earth’s orbit. Then, Earth periodically would be changing its position with respect to the “fixed” stars. Angular radius (α) is in average of 23.45° along the changing of the Earth position |
5. Conclusions
This work describes the hypothesis where the explanation of the Earth’s axial precession can be based on the relativistic solution. Then, this work shows the use of Eq. (1) derived from the solution of General Relativity, which considers all the forces and energies involved in a rotating system, applied here to estimate the axial precession. In this solution, the entire Solar System disk would rotate as a solid (or rigid) body, so that the Earth changes its position with respect to the stars that we can consider as "fixed" stars. Then, we define Eq. (17), which also considers the advancement of the Earth’s orbit due to the apsidal precession to estimate the period of Earth’s axial precession, and comparing our estimates we find a good approximation with the observations. One of the important significances of the result of this work is that for the explanation of the Earth’s axial precession it is possible to use the relativistic solution to find the known period of the axial precession, since in this solution the total net or absolute force considers a third term, which includes the force related to the Coriolis force in a rotating system, which is inverse of the distance to the fourth power; while the classical Newtonian total force, derived from the Newtonian theory of gravitation, only considers two terms, which are the Newtonian force of gravity and the centrifugal force, then having some limitations proper to this type of classical theory, and does not consider all the forces and energies involved in a rotating system. This is the reason why in the classical solution is necessary to add some external gravitational forces to the rotating system to adjust the calculations of classical mechanics to the observations. Thus, according to classical dynamics, axial precession depends mainly on the gravitational forces exerted by the Moon and the Sun on Earth’s equatorial bulge, so that if the Earth were hypothetically a perfect sphere, those gravitational forces would not be producing any torque or moment of inertia on the Earth and there would be no change in the direction of the Earth’s axis, and there would be no axial precession.On the other hand, the relativistic solution is different comparing to the Newtonian theory and to the classical dynamics considerations, mainly with regard to rotating systems, and does not require adding any other external gravitational force to fit it to the observations, and the axial precession only depends on the entire Solar System disk being rotating like a solid (or rigid) body, so the gravitational forces of the Moon, Sun and other planets on Earth’s equatorial bulge would not affect to have axial precession. The next step to probe the cause of the Earth’s axial precession is to make more detailed observations and comparisons of the motion of the other planets with respect to the "fixed" stars, in order to verify whether the behaviour and dynamics of the entire Solar System disk behaves according to the relativistic solution and it rotates like a solid body.
ACKNOWLEDGEMENTS
The author would like to thank Professor Sergio S. Cornejo for its review and comments for this work.
References
| [1] | Hohenkerk, C.Y., Yallop, B.D., Smith C.A., Sinclair, A.T., 2006, Celestial Reference Systems, in Seidelmann, P.K., editor. Explanatory supplement to the astronomical almanac, University Science Books, Mill Valley. |
| [2] | Main, R., 1863, Practical and Spherical Astronomy (Cambridge) pp.203–4. |
| [3] | Williams, J. G., 1994, Contribution to the Earth’s Obliquity Rate, Precession, and Nutation. The Astronomical Journal. 108: 711. |
| [4] | Cornejo, A. G., 2014, A lagrangian solution for the precession of Mercury’s perihelion, Int. J. Astron. 3, 31–34. |
| [5] | Einstein, A., 1955, The Meaning of Relativity, 5th ed. Princeton University Press, Princeton. |
| [6] | Arbab, A. I., 2012, J. Mod. Phys., Vol. 3 No. 29, 1231-1235. arXiv:1105.1911 [physics.gen-ph]. |
| [7] | Cheng, T., 2005, Relativity, gravitation, and cosmology, Oxford University Press. pp. 98–99. |
| [8] | Unzicker, A., 2008, Why do we Still Believe in Newton’s Law? Facts, Myths and Methods in Gravitational Physics. arXiv:gr-qc/0702009v8. |
| [9] | Scarborough, J. B., 1958, The Gyroscope: Theory and Ap-plications, New York: Interscience Publishers, Inc., pp. 37-52. |
| [10] | Einstein, A., 1915, Erklärung der Perihelbewegung des Merkur aus der allgemeinen Relativitätstheorie. Königlich Preußischen Akademie der Wissenschaften (Berlin) 47(2) pp. 831-839. |
| [11] | Beatty, J. K., Petersen, C. C., Chaikin, A. and Chaikin, A. L., 1990, The New Solar System, 4th ed., Cambridge: Cambridge University Press, pp. 193–198. |
| [12] | Cornejo, A. G., 2013, The rotating reference frame and the precession of the equinoxes. Lat. Am. J. Phys. Educ. Vol, 7(4), 591. |
| [13] | Cornejo, A. G., 2020, The rotational velocity of spiral Sa galaxies in the general theory of relativity solution, Int. J. Astron. 9(2): 27-30. |
| [14] | Williams, D. R., 2019, Planetary Fact Sheet – Metric, NASA, Houston, Texas. http://nssdc.gsfc.nasa.gov/planetary/factsheet. Accessed on June 9th, 2020. |



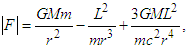
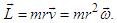
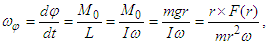
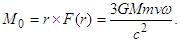
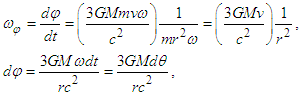
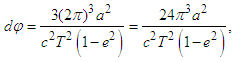
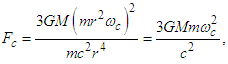
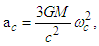
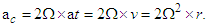
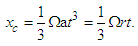
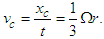
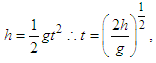
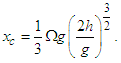
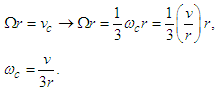
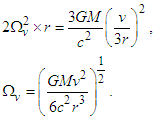
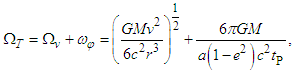
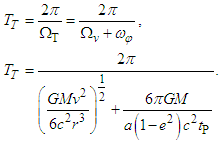
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML