-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Astronomy
p-ISSN: 2169-8848 e-ISSN: 2169-8856
2020; 9(2): 27-30
doi:10.5923/j.astronomy.20200902.01
Received: Dec. 6, 2020; Accepted: Dec. 20, 2020; Published: Dec. 26, 2020

The Rotational Velocity of Spiral Sa Galaxies in the General Theory of Relativity Solution
Adrián G. Cornejo
Electronics and Communications Engineering from Universidad Iberoamericana, Santa Rosa, Querétaro, Mexico
Correspondence to: Adrián G. Cornejo , Electronics and Communications Engineering from Universidad Iberoamericana, Santa Rosa, Querétaro, Mexico.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This work describes the hypothesis where the explanation of the rotational velocity of spiral Sa galaxies is based on the General Theory of Relativity solution. In this solution, a spiral Sa galaxy disk would rotate like a solid body, so that the stars into the spiral Sa galaxy must be rotating with the system at a uniform angular velocity. On these assumptions, we define the equation that describes the rotational velocity of stars in a spiral Sa galaxy based on the relativistic solution and present examples of the rotation curves of spiral Sa galaxies NGC 4378 and NGC 4594, comparing our estimates with the observations, finding a good approximation between the estimated rotation curves and the known rotation curves of these spiral Sa galaxies.
Keywords: Galaxies: spiral, kinematics and dynamics, General Theory of Relativity
Cite this paper: Adrián G. Cornejo , The Rotational Velocity of Spiral Sa Galaxies in the General Theory of Relativity Solution, International Journal of Astronomy, Vol. 9 No. 2, 2020, pp. 27-30. doi: 10.5923/j.astronomy.20200902.01.
Article Outline
1. Introduction
- One of the current problems of gravitation theory is to justify the large velocities observed for stars in spiral galaxies and how they differ from the rotational velocities of planets. Indeed, precise measurements (with a variety of techniques) of the velocities of stars and gases in spiral galaxies [1,2] make it clear that the action of the galaxy on its stars and gas estimated according to classical gravitation theory cannot account for the measured velocities, if the gas is assumed to be a stable component of the galaxy, as described by the quasi-stationary density wave theory, which characterizes spirals as rigidly rotating, long-lived patterns (i.e. steady spirals) [3].Thus, we can consider that in principle, stars and gas in spiral galaxies do not follow a rotational motion as described in classical gravitational theory, so they must obey other considerations to satisfy the observations.Currently, there are some plausible theories, but not yet proven and confirmed to date, which attempt to explain the rotational velocities observed in spiral galaxies. The most popular theory nowadays is the speculation that brings the dark matter concept [4], which has not been detected to date. In that theory, the dynamics of the stars in a spiral galaxy is described by the classical Newtonian theory of gravity, in which other forces are simply added due to the supposed dark matter that is considered part of a galaxy.A second theory, which is currently less popular, is that which considers the influence of gravitational effects of the faraway matter that come from other distant galaxies and massive structures [5]. In that theory, the dynamics of the stars in a galaxy is also described by the classical Newtonian theory of gravity, in which some other forces are added due to the faraway matter outside a spiral galaxy.Another theory that tries to solve the problem of the rotation of the spiral galaxy is the one that considers a gravito-magnetic field not yet discovered which influences the rotation curves of galaxies [6], among others.However, these theories do not directly consider the General Theory of Relativity (GTR) [7], which has been shown to be a predictive theory that has been able to coherently describe the dynamics and kinematics behaviour of most celestial bodies in space-time, and which also includes the classic Newtonian theory of gravity.Based on the General Theory of Relativity solution, we found that the rotational velocity of spiral Sa galaxies can be estimated from the total force equation for a rotational gravitational system solution derived from the General Theory of Relativity, being composed by the sum of the Newtonian force of gravity, the centrifugal force and a force related to the Coriolis force. This solution is different to the classical solution of the Newtonian force in the third term, since it includes the force with the inverse of the distance to the fourth power.In this solution, the dynamics of the stars in a spiral Sa galaxy is not exclusively due to the combined gravitational field of all the stars, gas and any other massive object in the galaxy, but rather considers that the entire galaxy moves and rotates as a solid body.The aim of this work is to describe the hypothesis where the explanation of the rotational velocity of some spiral Sa galaxies is based on the General Theory of Relativity solution. Thus, we define the equation that describes the rotational velocity of stars in a spiral Sa galaxy based on the relativistic solution. In particular, we show examples of the estimated rotation curves of spiral Sa galaxies NGC 4378 and NGC 4594 (with very different masses and sizes), comparing our estimates with the observations.
2. General Theory of Relativity Solution for the Total Force
- A relativistic solution for the angular movement of the celestial bodies in a rotational system can be determined from a study of the solutions of Einstein’s equations following the standard procedure [8,9,10]. Thus, the total force for a rotating system is given as
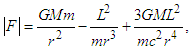 | (1) |
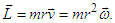 | (2) |
3. Rotational Velocity in a Spiral Sa Galaxy
- According to this relativistic solution, at the stage where a spiral Sa galaxy disk rotates like a solid (or rigid) body, the motion of the stars that form the spiral galaxy should be perceived from Earth as a uniform rotation of the galaxy. Taking into account the third term in Eq. (1), we can reduce common terms, giving
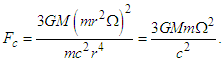 | (3) |
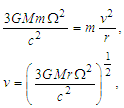 | (4) |
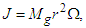 | (5) |
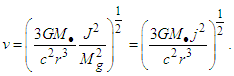 | (6) |
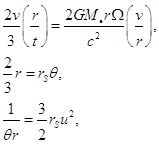 | (7) |
4. Comparison between Estimated and Observed Rotational Velocities in Spiral Sa Galaxies
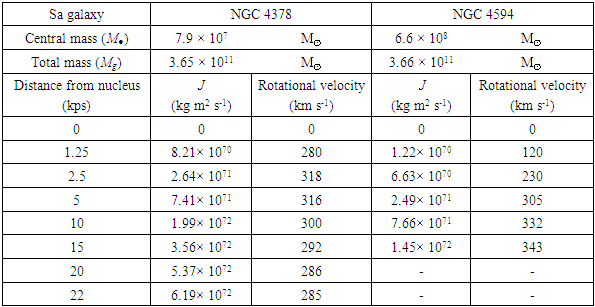
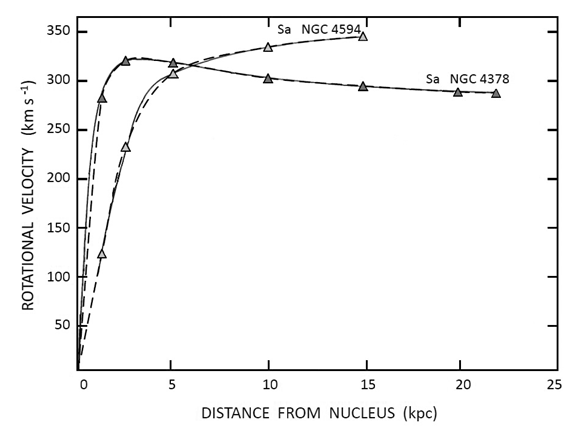
- Our purpose is to estimate the rotational velocity of some spiral Sa galaxies based on the relativistic solution and assuming their behaviour is like a solid body, plot the rotation curves with the estimated values and compare them with the observed rotation curves. In particular, we focus on the rotation curves of two spiral Sa galaxies. More precisely, we take as an example the known rotation curves of the spiral galaxies NGC 4378 and NGC 4594, assuming that the only relevant contribution to the movement of their different regions is from their behaviour as a solid body, and considering only the movements found on the galactic plane. Then, an estimation of the rotational velocity is given by Eq. (6), taking into account the known values for each of these two spiral galaxies [16,17,18]. These results are tabulated in Table 1 (Rotational velocities) for each galaxy.
|
5. Conclusions
- The aim of this work is to describe the hypothesis where the explanation of the rotational velocity of some spiral Sa galaxies is based on the General Theory of Relativity solution. Then, this work shows the using of Eq. (1) derived from the General Relativity solution, here applied to estimate the rotational velocity of some spiral Sa galaxies. Then, we define Eq. (6) to describe the rotational velocity of stars in some spiral Sa galaxies based on this solution, and present preliminarily two examples of the rotation curves of spiral Sa galaxies NGC 4378 and NGC 4594, then comparing our estimates with the observations, finding a good approximation between the estimated rotation curves and the known rotation curves of these spiral Sa galaxies. One of the significances of this result based on the General Theory of Relativity solution is that it is hypothetically possible to fit the known rotation curves of the spiral Sa galaxies without any need of introducing dark matter at all. The next step in probing the galaxy dynamics on the General Relativity solution is to make more detailed observations to confirm whether the way in which spiral Sa galaxies rotate is mainly according to rigidly rotating and long-lived patterns, as steady spirals.
ACKNOWLEDGEMENTS
- The author would like to thank Professor Sergio S. Cornejo for its review and comments for this work.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML