1. Introduction

Dark energy and dark matter are generally considered as distinct phenomena, and most ongoing attempts to explain them offer separate explanations. Also, the explanations tend to be phenomenon centric.

As far as dark energy is concerned, the question isn’t so much ‘what is dark energy?’ – that is already answered by the cosmological constant – but ‘why is there dark energy?’ Keeping this in mind, in previous papers by the author [4, 5], the philosophy of approach has been to identify the physical principle behind the phenomenon of dark energy. It has been proposed that the accelerating expansion of the universe is due to the cosmologicalization of the principle of equivalence in an expanding spherical distribution of matter – whereby, the inertial mass of an object on the surface of the sphere has to exist in a spacetime accelerating frame of reference, parametrized by the cosmological constant.

As for dark matter, most of the existing propositions have been quantum mechanical. However, none of them seems to have satisfactorily addressed the issue of continued failure to directly detect dark matter. Direct undetectability of dark matter seems to be a problem belonging more to classical mechanics than quantum mechanics. Here again, in a previous paper [5] the author has invoked the cosmologicalization of the principle of equivalence - in this case, the weak principle of equivalence. It has been proposed that dark matter are objects in cosmological freefall, which never experience inertia, and are therefore immaterial in nature and not directly detectable.

While these propositions provide a broad conceptual framework in explaining the nature of dark energy and dark matter, it leaves an important issue unaddressed. Why is it that spacetime force and inertial force on objects do not cancel in cosmological acceleration, allowing the objects to experience inertia, while spacetime force and inertial force on objects are cancelled in cosmological freefall, whereby the objects do not experience inertia?

This paper provides the answer to the question.

2. Extrinsic Inertial Mass and Acceleration

According to quantum field theory, massless particles originally in uniform motion c acquired mass at electroweak symmetry breaking via the Higgs particle, and the Higgs particle itself acquired mass as well [1, 2, 3]. It is also possible, however, to consider an analogous classical paradigm of the quantum field process of manifestation of mass in objects, by invoking the concept of inertia, whereby objects originally in uniform motion c experiences inertia when resisting deceleration by the Higgs fields, and the experience of inertia constitutes the manifestation of inertial mass in the objects.¹

We may call objects whose mass is manifested as a consequence of experiencing inertia due to resistance of the objects originally in uniform motion to deceleration by the Higgs fields as extrinsic inertial mass objects. Once manifested as extrinsic inertial objects, however, they can experience inertia again, when they resist local deceleration/acceleration from a state of uniform motion/rest.

3. Extrinsic Inertial Mass Objects and Cosmological Acceleration

Since objects originally in uniform motion experience inertia universally resisting deceleration by the Higgs fields, whereupon extrinsic inertial mass of objects is manifested, and since extrinsic inertial mass objects can experience inertia again resisting local deceleration/acceleration from a state of uniform motion/rest, is there a way extrinsic inertial mass objects can experience inertia again universally by resisting universal acceleration from a preferred state of rest?²

In previous papers [4, 5] the author has proposed that the principle of equivalence – which recognizes momentary equivalence between gravitational force and inertial force – is cosmologicalized in an expanding spherical distribution of matter, whereby, spacetime itself acts as the accelerating frame of reference – parametrized by the cosmological constant, as in 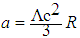– of the inertial mass of an object on the surface of the sphere, and the inertial force thus generated is momentarily equivalent at a certain radial distance to the gravitational force experienced by the gravitational mass of the object.

Since an object can be considered to be situated on the surface of any expanding spherical distribution of matter, inertia would be experienced universally by all extrinsic inertial mass objects. There is direction in the force on an object, and since inertial force arises in an equal and opposite way, the object also experiences inertia in the direction of the inertial force. When considering an object on the surface of an expanding spherical distribution of matter, the direction of motion of the object would be away from the centre of the sphere, and therefore the inertial force generated on the extrinsic inertial mass of the object would be directed toward the centre of the sphere and the object would therefore be experiencing inertia in the same direction as well. Cosmologically, however, an object can be considered to be situated on the surface of any spherical distribution of matter, and the overall motion of the object would therefore have no unique direction – it will be seen to be receding from every direction, and therefore would experience inertia omnidirectionally. Thus, the universal experience of inertia by extrinsic inertial mass objects is omnidirectional.

4. Intrinsic Inertial Mass and Freefall

An object in gravitational freefall does not experience inertia because the inertial force on its inertial mass is cancelled by the equal and opposite gravitational force on its gravitational mass.³ The inertial force on the inertial mass of the object arises locally and which is cancelled locally by the gravitational force on the gravitational mass of the object, rendering the object weightless in a locally inertial frame of reference. However, the ‘global’ acceleration due to gravity continues acting on the gravitational mass of the object, whereby freefall in a ‘global’ non-inertial frame of reference continues.

Since it is possible to calculate the kinetic energy of an object in freefall and compare it with its potential energy to evaluate conservation of energy, it suggests that the inertial mass of the object can also be seen as an intrinsic property, whereby the object does not have to experience inertia for it to possesses inertial mass.

For an object to resist acceleration/deceleration from a state of rest/uniform motion, it would have to be physically identifiable in its state of rest/uniform motion for acceleration/deceleration to be able to act on the object. It is reasonable to infer therefore that mass has to be an identifying property of the object for acceleration/deceleration to be able to act on before the object can resist that acceleration/deceleration with equal and opposite inertial force. Mass which is necessary to resist acceleration/deceleration has to be therefore seen as an intrinsic property of objects, and we may call it intrinsic inertial mass of objects.

Manifestation of extrinsic inertial mass objects occurred when objects in uniform motion were decelerated in interaction with the Higgs fields. Those objects would have possessed intrinsic inertial mass, upon whose deceleration the intrinsic inertial mass of the objects experiences inertia, whereupon extrinsic inertial mass of the objects is manifested. This does not mean, however, that intrinsic inertial mass of an object ceases to exist because its inertia manifests as extrinsic inertial mass. Manifestation of extrinsic inertial mass is physical proof that intrinsic inertial mass is experiencing inertia, and for extrinsic inertial mass to continue to be manifested, intrinsic inertial mass must continue to experience inertia – thus, intrinsic inertial mass co-exists with extrinsic inertial mass in extrinsic inertial mass objects.

A locally or cosmologically accelerated extrinsic inertial mass object experiences inertia because the applied real force which acts on the extrinsic inertial mass of the object is not cancelled by the arising inertial pseudo force on the intrinsic inertial mass of the object.

In gravitational freefall of an object, the gravitational force on the gravitational mass of the object is cancelled by the arising inertial force on the intrinsic inertial mass of the object. Equivalence between gravitational and inertial mass of an object is therefore between gravitational and intrinsic inertial mass of the object.

An object in a locally inertial frame of reference in gravitational freefall can be also seen to be equivalent to a stationary object, i.e., that which is in an inertial frame of reference, which with respect to an accelerating frame of reference creates an impression of freefall of the object in the opposite direction from the perspective of an observer in the accelerating frame of reference. The observer in the accelerating frame of reference, however, interprets the impressional freefall of the object in terms of cancellation between the force of impressional accelerating frame of reference and inertial force on the inertial mass of the object, whereby the object does not experience inertia.⁴ However, because the impressional accelerating frame of reference has to be a pseudo-like force (it is the equivalent of the pseudo-like force of gravitational acceleration on the gravitational mass of an object in gravitational freefall) for it to be cancellable by the arising inertial pseudo force, it can only act on intrinsic inertial mass of an object (as discussed, intrinsic inertial mass is associated with inertial pseudo force, and therefore it stands to reason that the pseudo-like force of the impressional accelerating frame of reference will also only act on intrinsic inertial mass of an object).

Since impressional force only acts on intrinsic inertial mass, it is not necessary therefore that an object has to be an extrinsic inertial mass object, which possesses intrinsic inertial mass, to participate in impressional freefall. We may well envision objects which only possess intrinsic inertial mass and which therefore can only participate in impressional freefall. We may call such objects intrinsic inertial mass objects.

When an object is on the ground of mass M, the gravitational mass 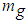of the object experiences gravitational force 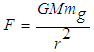as the weight of the object because of the normal force N from the ground, which is acting on the inertial mass 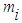of the object with equal and opposite force 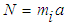. According to the principle of equivalence, this is equivalent to an inertial mass undergoing acceleration a whereby 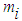is subjected to force 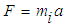(which is the equivalent of normal force 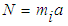and generates equal and opposite inertial force 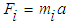(which is the equivalent of gravitational force 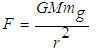)⁵.

A gravitational mas 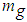experiencing gravitational force 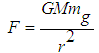on a gravitational surface of mass M involves gravitational acceleration 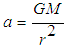; gravitational acceleration is also involved in gravitational freefall of a gravitational mass 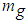. Since gravitational acceleration is responsible for gravitational mass experiencing gravitational force on a gravitational surface, as well as a gravitational mass not experiencing gravitational force in gravitational freefall, we may call gravitational acceleration as ‘gravitational mass universal accelerator’.

In the extended weak principle of equivalence, we have a stationary inertial mass with respect to an accelerating frame of reference, which produces an impression of freefall of the inertial mass. Now, if the observer in the accelerating frame of reference is considered as an inertial mass then it would be experiencing inertial force in the same direction as the impression of freefall of the stationary inertial mass. In effect, the acceleration of one frame of reference generates two accelerating frames of reference: one real, wherein inertial mass experiences inertia, and the other impressional, wherein inertial mass does not experience inertia. We may call such acceleration which produces the dual effect of inertial mass experiencing inertia, as well as inertial mass not experiencing inertia, as ‘inertial mass universal accelerator’.

Now, since it has been here proposed that extrinsic inertial mass objects experience inertia cosmologically, is there a way for intrinsic inertial mass objects to not experience inertia cosmologically?

5. Intrinsic Inertial Mass Objects and Cosmological Freefall

In a previous paper [5] the author has proposed that the spacetime accelerating frame of reference that is involved in the cosmologicalization of the principle of equivalence can also function as the spacetime accelerating frame of reference of the cosmologicalization of the weak principle of equivalence, and that objects accelerated by it can be considered to be in cosmological freefall.

It is here proposed that the spacetime accelerating frame of reference acts as an inertial mass universal accelerator, parametrized as 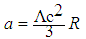, which acts as a real force on extrinsic inertial mass objects, and because it does not canccel the arising inertial pseudo force on the objects, allows extrinsic inertial mass objects to experience inertia in cosmological acceleration; and it also acts as a pseudo-like force on intrinsic inertial mass objects, and because it cancels the arising inertial pseudo force, prevents intrinsic inertial mass objects from experiencing net inertia in cosmological freefall.^6,7

In local impressional freefall of an inertial mass object with respect to an accelerating frame of reference, the impressional freefall is in the opposite direction of the accelerating frame of reference. In cosmological freefall, even though the intrinsic inertial object is travelling in the same direction as an extrinsic inertial mass object in cosmological acceleration on the surface of an expanding spherical distribution of matter, because there is cancellation between the pseudo-like force of spacetime accelerating frame of reference and inertial pseudo force on the intrinsic inertial mass object, whereby the object does not experience, it constitutes sufficient condition for freefall.

Since extrinsic inertial mass objects experience inertia and are material, it is reasonable to infer that intrinsic inertial objects which do not experience net inertia would therefore be immaterial. The presence of intrinsic inertial mass objects would therefore only ever be possible to infer through the gravitational effect of their equivalent gravitational mass. It is proposed that it is intrinsic inertial mass objects in cosmological freefall that are the dark matter in the universe.

As discussed, an extrinsic inertial mass object in cosmological acceleration on the surface of any expanding spherical distribution of matter experiences its inertia omnidirectionally; similarly, an intrinsic inertial mass object in cosmological freefall on the surface of any expanding spherical distribution of matter would not experience its inertia omnidirectionally.

6. Conclusions

Inertial mass is manifested in two forms: material extrinsic inertial mass and immaterial intrinsic inertial mass. Visible matter is constituted of extrinsic inertial mass and intrinsic inertial mass. Local acceleration allows visible matter to experience inertia due to non-cancellation between applied real force on its extrinsic inertial mass and arising inertial pseudo force on its intrinsic inertial mass. Cosmological acceleration allows all visible matter to experience inertia all the time due to non-cancellation between spacetime real force on extrinsic inertial mass and inertial force on intrinsic inertial mass of visible matter. Visible matter in gravitational freefall does not experience inertia because of the cancellation between gravitational force on gravitational mass and inertial force on intrinsic inertial mass. Dark matter is constituted solely of immaterial intrinsic inertial mass, which does not experience inertia, being in cosmological freefall, because of cancellation between spacetime pseudo-like force and inertial pseudo force on intrinsic inertial mass of dark matter.

Notes

1. Since only a pseudo-like force can act on intrinsic inertial mass, the Higgs fields which at electroweak symmetry breaking decelerated intrinsic inertial mass of objects originally in uniform motion, would also exert a pseudo-like force. Since the pseudo-like force would be facing the arising inertial pseudo force, the two forces would not cancel each other, and inertia would therefore be experienced, whereupon, extrinsic inertial mass is manifested. As discussed about inertial mass universal accelerator, a pseudo-like force which acts on intrinsic inertial mass can also act as a real force on extrinsic inertial mass. It stands to reason therefore, that the Higgs fields which universally decelerates intrinsic inertial mass acting as a pseudo-like force, can therefore also act as a real force on manifested extrinsic inertial mass, thereby making the Higgs fields an inertial mass universal decelerator. The real force of the Higgs fields on extrinsic inertial mass would, however, be redundant, since the Higgs fields’ pseudo-like force acting on intrinsic inertial mass would have already decelerated the objects – the objects would not therefore experience inertia again because of Higgs fields’ real force on extrinsic inertial mass. Contrastingly, objects subjected to spacetime inertial mass universal accelerator experience inertia with real force acting on extrinsic inertial mass, and do no experience inertia with pseudo-like force acting on intrinsic inertial mass.

2. Locally, extrinsic inertial mass objects resist acceleration from a relative state of rest. Cosmologically, however, extrinsic inertial mass objects were never physically in a ‘state of rest’ – once manifested they are in the Hubble flow. Thus, the concept of ‘state of rest’ has to be modified to ‘preferred state of rest’: extrinsic inertial objects resist universal acceleration from a ‘preferred state of rest’.

3. Inertial force is a pseudo force; since it is cancelled by gravitational force it implies therefore that gravitational force is a ‘pseudo-like’ force (cf. footnote 5).

4. This aspect of impressional freefall has not been well-examined uptil now. It has been simply accepted that since the object is stationary no force is acting on it. However, from the perspective of the object with respect to the accelerating frame of reference, and from the perspective of the accelerating frame of reference with respect to the object, the object is in impressional freefall - in other words, the object is subjected to an impressional force. It must then be explained why is impressional force cancelled by inertial force when the object is in impressional freefall, whereas if that same object were to be accelerated by a real force, it is not cancelled by inertial force - even though in both the cases the applied force is acting on the inertial mass of the object.

5. This equivalence of gravitational force and inertial pseudo force implies that gravitational force is a ‘pseudo-like’ force (cf. footnote 3).

6. The pseudo-like force of spacetime accelerating frame reference also acts on intrinsic inertial mass of extrinsic inertial mass objects and is cancelled by arising inertial pseudo force; however, because the real force of spacetime accelerating frame of reference on the extrinsic inertial mass of extrinsic inertial mass object is not cancelled by the arising inertial pseudo force, extrinsic inertial mass objects therefore experience inertia in cosmological acceleration.

7. As with extrinsic inertial mass objects resisting cosmological acceleration from a ‘preferred state of rest’, intrinsic inertial mass objects would also be resisting cosmological freefall from a ‘preferred state of rest’. However, intrinsic inertial mass objects have always been in the Hubble flow and resisting cosmological freefall from a preferred state of rest – unlike extrinsic intrinsic mass objects, which were originally in uniform motion as intrinsic inertial mass objects, and after being decelerated at electroweak symmetry breaking came to be in the Hubble flow as extrinsic inertial mass objects, and thereafter has been resisting cosmological acceleration from a preferred state of rest.