Chifu E. Ndikilar1, Hafeez Y. Hafeez1, 2
1Physics Department, Federal University Dutse, Jigawa, Nigeria
2SRM Research Institute, SRM University Kattankulathur, Chennai, India
Correspondence to: Hafeez Y. Hafeez, Physics Department, Federal University Dutse, Jigawa, Nigeria.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
The mechanics of star interiors has remained a subject of much research concern. Many theories have been proposed to account for the behavior of stars. However, these theories have one shortcoming or the other. A star model based on general relativity theory and current astrophysical observations was recently proposed. High gravitational forces, mass concentration in cores, rapid rates of spin and high centripetal forces gives stars their spheroidal shapes. In this article, the gravitational metric tensor of a spherically symmetric sphere containing a non compressible liquid is extended to formulate an oblate spheroidal plasma star model. Using removable space singularities at the Hilbert radius and in outer space, the plasma stars are classified into three major groups (regular, neutron stars and pulsars, black holes). The metric tensor for an oblate spheroidal liquid star obtained has six non zero components as opposed to four for spherical plasma star model.
Keywords:
General Relativity, Oblate spheroidal star, Metric tensor, Space breaking, Plasma
Cite this paper: Chifu E. Ndikilar, Hafeez Y. Hafeez, General Relativity Model for Oblate Spheroidal Plasma Stars, International Journal of Astronomy, Vol. 8 No. 1, 2019, pp. 13-19. doi: 10.5923/j.astronomy.20190801.03.
1. Introduction
Conventionally, stars in the universe are assumed to be gaseous spheres in nature in most researches. These stars are considered to consist mainly of hydrogen and their interiors are very inhomogeneous. The extremely hot and dense central region of the stars is considered to have hydrogen which is involved in an energy release process to the exterior [1, 2]. This conventional method assumes that helium is produced from hydrogen in an exothermic reaction (thermonuclear fusion) [3]. Other unpopular star models have been suggested over the years. In one of such models, the interior of a star is assumed to be made up of different states of matter conjectured within it [4]. Another model suggests that a non nuclear stellar energy source, low temperature and density characterize the star interior [5].In the 1920’s [6, 7], the first liquid star model was developed. This model suggest that the internal constitution of stars is much populated. There were many astrophysical evidences in support of this model but it was not convincing to the scientific world. The model had no sound mathematical framework and was formulated mainly on arguments and observational analysis. Conversely, Eddington’s gas model of stars had a well formulated mathematical background. This gas model gave a good theoretical explanation of the mass-luminosity relation (an important relation in observational astrophysics). Presently, this theory is still considered to be generally true. The inconsistencies of the gas model with observational astrophysical facts are usually considered to be “difficulties” that will be resolved in the future [1].The underlying principle of the gas model of star interior is based on the equation of heat equilibrium and the equation of mechanical equilibrium. For mechanical equilibrium it is expected that pressure inside the star is equal to the weight of any unit volume of star. On the other hand, if for any unit volume of the star, the energy produced equals energy flow from inside the star then there is energy balance or heat equilibrium. It is worth noting that these two equilibrium conditions do not depend on the state of the stellar matter (gas, liquid, or something else). The ideal gas equation of state introduced into the two fundamental equations gives the gas model of stars and all its deductions. [1, 2].Jeans’ liquid star theory of liquid stars follows an entirely different approach. Note that for an ideal liquid, the equation of state from classical physics is simple. Further deductions from the equations of equilibrium are not possible as it does not contain characteristics of stellar mass. [6, 7]. Due to these shortcomings of thermodynamics and classical mechanics, Borrissova and Rabounski [1] introduced an absolutely different approach to the problem of stellar theory. This approach is based on the General Theory of the gravitational field within a liquid star. This approach is very convincing as recent astrophysical observations show that there is condensed matter with star interiors. Particularly, it has been observed that the Sun consists of metallic hydrogen at high temperatures and in liquid state [7, 8].In this article, the spherical liquid star model is extended to oblate spheroidal liquid stars. The rationale behind this extension is the fact that the spherical liquid star model assumes stars to be perfectly spherical bodies. It is well known that the Sun and other stars are more precisely oblate spheroidal in geometry. Also, pulsars and neutron stars are thought to consist mainly of spinning neutron cores that are very densely packed. It is always assumed that stars have spherical shape though the forces acting within a star turn to suggest that this assumption is possibly false. High gravitational forces, mass concentration in cores, rapid rates of spin and high centripetal (centrifugal) forces makes stars to be spheroidal in geometry. Hence, the need to extend the spherical liquid star model to more satisfactory astrophysical spheroidal stars.
2. General Relativity Liquid Spherical Star Model
Here, we review the major components of the General Relativity liquid star model. This is very necessary to lay the foundation for the extension to oblate spheroidal star model.In this model, stars are considered to be perfectly spherical in shape and composed of light and matter. Gravitational fields of stars are also considered to be spherically symmetric. Thus, in the formulation of the theory of General Relativity for stars; the matter, structure and gravitational field should be given by a spherically symmetric space-time metric. Basically, there are only three derived gravitational metrics that explain symmetric spherical gravitational fields. These are Schwarzschild mass-point metric, Schwarzschild metric of an incompressible liquid sphere and de Sitter’s metric for a spherical physical vacuum.The Schwarzschild metric of an incompressible liquid sphere is of interest to us in this article. This metric in a truncated form with many limitations was introduced by Schwarzschild [1,9]. The limitations in the metric were pre-imposed during its derivation to avoid breaking in the gravitational field. The most complete form of the metric was introduced in 2009 [10]. This metric accounts for space breaking and is free of limitations. The metric of a space filled with an incompressible fluid in its complete form is given as [1, 10];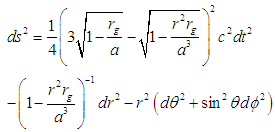 | (1) |
where 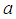 is the physical radius of the sphere,
is the physical radius of the sphere, 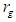 is the Hilbert radius of the astrophysical body given as
is the Hilbert radius of the astrophysical body given as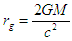 with
with 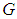 as the gravitational constant and
as the gravitational constant and 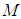 its mass. If the radial distance
its mass. If the radial distance 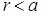 , then the metric describes the interior of the sphere of incompressible fluid. At the surface, we have
, then the metric describes the interior of the sphere of incompressible fluid. At the surface, we have 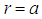 which makes the metric to coincide with that of a mass point. Also, the outer metric is the same as that of the mass point.Components (covariant and contravariant) of the gravitational inertial force are obtained by substituting the differential of the gravitational potential with respect to the coordinates into the gravitational force formula [1]. This gives:
which makes the metric to coincide with that of a mass point. Also, the outer metric is the same as that of the mass point.Components (covariant and contravariant) of the gravitational inertial force are obtained by substituting the differential of the gravitational potential with respect to the coordinates into the gravitational force formula [1]. This gives: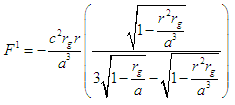 | (2) |
and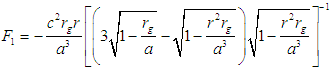 | (3) |
Within the sphere, r < a and F1 < 0. Thus, the force is attractive with magnitude dependent on the radial distance r. Note that gravitational force vanishes at the centre and increases to maximum at the surface of the sphere. Thus, the curvature space inside of a liquid sphere is not a constant but varies with distance.The new model of liquid stars based on General Relativity is formulated using equation (1). Thus, in the star’s interior, the gravitational force varies with distance from the centre of the spherical star. Exterior to the star, the well known Newtonian force acts which can be deduced from the metric of a mass-point. The force is inversely proportional to the distance from the star.It is worth noting that, the field within liquid spheres is not continuous and space breaking occurs at two distances from the liquid spheres centers. The violation of signature conditions of the space metric gives rise to space breaking. The space will therefore have a singularity in the region where there is violation of not less than one of the signature conditions. The signature conditions for a sign- alternating diagonal metric (+ - - -) has signature conditions that are same as those of the four dimensional pseudo-Riemannian space and has form [1, 11].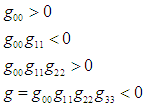 | (4) |
Weak signature conditions are represented by the first three conditions. The fourth represents the strong signature condition. A removable singularity occurs when there is violation of all or one of the weak signature conditions and non violation of the strong signature condition. A singularity is not removable if there is violation of the strong signature condition. The gravitational field of a non removable singularity though mathematically sound has no physical interpretation.Now, for a liquid sphere, the exterior metric is given [1] as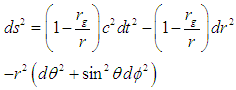 | (5) |
The first signature condition is violated at g00 = 0, r = rgThat is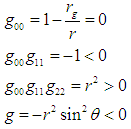 | (6) |
It can be deduced for the interior metric that there is violation of three signature conditions (2nd, 3rd and 4th) at the radial distance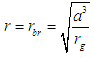 | (7) |
from the center of the sphere. Thus: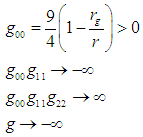 | (8) |
Hence, for the gravitational field of a liquid spherical star, space breaking occurs at two distances from the center:i. At the surface spherically covering the star’s center of gravity at the distance r = rg (Hilbert’s radius). For most stars, this surface occurs at distances much smaller than their physical radius. This space breaking is sometimes called the inner space breaking.ii. On the surface of the sphere covering the mass at the distance rbr. This distance is called the outer space breaking and is far greater than the radius (physical) of most stars.The liquid star model thus introduces a novel classification of stars based on the position of space breaking in the gravitational field relative to the star’s physical surface [1].a) Regular Stars: In this case, the physical radius a of the star is far greater than the Hilbert radius or collapsed core (rg) i.e. a >> rg. The space breaking (outer) is found possibly in cosmos, a distance away from the star. All the visible stars belong to this group e.g the Sun, dwarfs and white dwarfs.b) Neutron Stars and Pulsars: Here, the physical radius and Hilbert radius are almost the same but does not equal (otherwise it will become invisible and cannot be observed). rg ≤ a. Thus, space breaking (in the outer cosmos) is very close to the star’s surface (though it does not reach it).c) Black Holes: At the physical surface, the Hilbert radius and the outer space breaking radius meet i.e rg = a = rbr.
3. Oblate Spheroidal Star Model
In this section, we develop an extension of the spherical liquid star model to obtain an oblate spheroidal liquid star model.
3.1. Motivation
The assumption that stars are spherical is not true generally considering the forces acting on it. The concentration of mass the cores of stars, the high gravitational forces, high spin rates and extremely high centripetal forces all suggest that the shapes of stars and most especially neutron stars are spheroidal. The rotation of the Earth, though small is sufficient enough to make it swell at the equator forming an oblate spheroid (Fig. 1). Thus, the interplay of centripetal and gravitational forces equally makes the stars spheroidal in shape [12].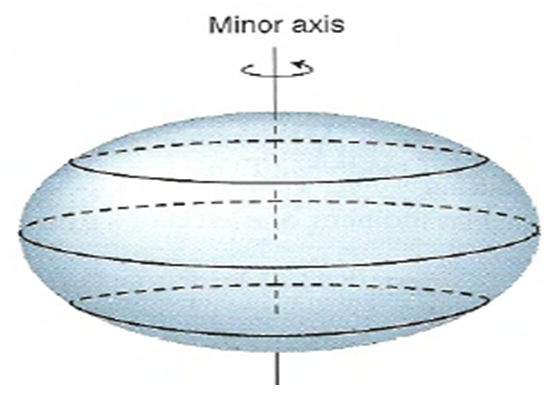 | Figure 1. Rotating spherical Earth bulges out into an oblate spheroid |
Rotation of a non rigid spherical object makes it to bulge at the equator to become an oblate or Maclaurin spheroid. Stars are known to be made of matter that is spinning and hence their shapes are spheroidal. Neutron star astronomers are aware of the possibility that spin can contribute to their understanding of the physics neutron stars e.g. effects of non-spherical shape on the orbit of a pulsar-pulsar binary [13].The lunar-solar precession driven flow in the Earth’s liquid core has been studied extensively with the Earth having an oblate spheroidal shape. The geophysical significance of the abundant energy and the persistent nature of precession in an oblate spheroid is eminent. [14]It has been shown by observations that stars are not perfectly spherically symmetric. They are deformed by rotation and magnetic fields. The study of stellar shapes has been possible using optical interferometry for a few of the nearby fast rotating stars. Also, asteroseismic measurements, with much better precision than interferometry, has been used to measure the asphericity of an A-type star. This has shown that the star is oblate spheroidal in shape [15].It is well known that interiors of giant planets have immense pressures and high densities, but there are few research works on their departures from axisymmetry. The effect of density varying internally on gravitational attraction to the oblate has been of particular interest [16].This model is an attempt to extend the study of gravitation in spherical plasma stars to their precise shape (oblate spheroid). Obviously, the oblate spheroidal geometries of these stars have corresponding effects on their gravitational fields and hence the motions of test particles in these fields. These effects include gravitational spectral shift of light, gravitational length contraction and gravitational time dilation.
3.2. The Model
The invariant line element in the interior of a spherical liquid star can be deduced from equation (1) as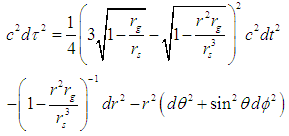 | (9) |
where 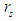 is the radius of the spherical liquid star and
is the radius of the spherical liquid star and 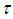 is the proper time.Now, using deformation, the spherical liquid star can be transformed to take the shape of an oblate spheroidal liquid star. Suppose, the deformation is such that the mass Mo and density ρo of the star remain unchanged. Then, its surface parameter expressed in the oblate spheroidal coordinates system is [17, 18] as
is the proper time.Now, using deformation, the spherical liquid star can be transformed to take the shape of an oblate spheroidal liquid star. Suppose, the deformation is such that the mass Mo and density ρo of the star remain unchanged. Then, its surface parameter expressed in the oblate spheroidal coordinates system is [17, 18] as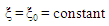 | (10) |
Using tensor analysis, we can state that, Einstein’s gravitational field equations in the interior region of an oblate spheroid liquid star are geometrically equal to the spherical liquid star equations. Hence, the field equations in both coordinate systems are connected by coordinate transformations between spherical and oblate spheroidal coordinate systems. Thus, the interior line element of an oblate spheroidal liquid star is deduced as follow:i. Noting that the Hilbert radius rg is a constant for the oblate liquid star despite the deformation into an oblate spheroid (based on its definition in equation (1)). It is also convenient to replace rs, the radius of the spherical liquid star by the corresponding radius of the oblate spheroidal liquid star, rab, which in this case will no longer be constant along the surface of the star due to symmetry considerations. An equatorial radius and polar radius will then come into play.ii. Transform the world line element, from spherical to oblate spheroidal coordinates on the right hand side of equation (9). This is informed by the fact that the line elements in both coordinates are the same from tensor analysis. That is (ct, r, θ, φ) is transformed to (ct, η, ξ, φ).Spherical polar coordinates and oblate spheroidal coordinates are related as follows [17, 18];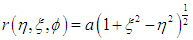 | (11) |
and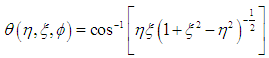 | (12) |
Using equations (11) and (12) it can be shown that: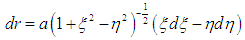 | (13) |
and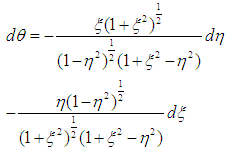 | (14) |
Also, 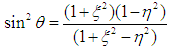 | (15) |
Now, using equations (13) to (15) in the world line element; equation (9) gives the non-vanishing components of the covariant tensor in the interior region of a homogeneous liquid oblate spheroidal star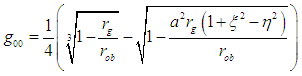 | (16) |
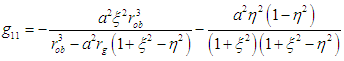 | (17) |
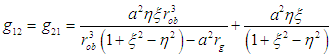 | (18) |
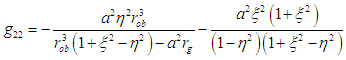 | (19) |
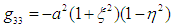 | (20) |
Equations (16) to (20) represents the internal covariant metric of an oblate spheroidal star filled with an incompressible fluid (which could be plasma as in the Sun). This tensor describes the gravitational field, internal structure and matter of the star.The external field (exterior region of the star) can be described using the tensor [17, 18]: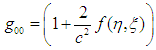 | (21) |
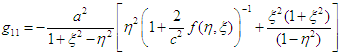 | (22) |
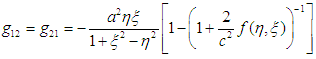 | (23) |
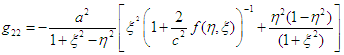 | (24) |
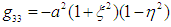 | (25) |
where the distribution of mass determines the function 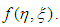 Now, space breaking due to the internal and external metric can be investigated according to the signature prescription given in equation (4).For the external field, the line element is
Now, space breaking due to the internal and external metric can be investigated according to the signature prescription given in equation (4).For the external field, the line element is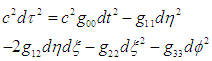 | (26) |
Rearranging equation (26), we can write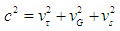 | (27) |
or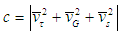 | (28) |
where the space velocity (vs), velocity of local time (vτ) and gravitational velocity(vG) are defined as: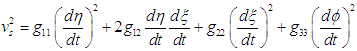 | (29) |
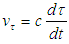 | (30) |
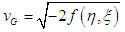 | (31) |
In the absence of gravity (and hence acceleration); the gravitational velocity vanishes and equation (27) takes the form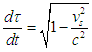 | (32) |
It can be deduced from (28) that the gravitational velocity can never exceed the speed of light. Thus, the maximum value that space velocity, velocity of local time and gravitational velocity is the magnitude of the speed of light.At the equator of an oblate spheroidal mass, f (η, ξ) is approximated [19] as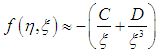 | (33) |
where C and D are constants that are unique for a given astrophysical body and are defined in [19]. Now, setting the gravitational velocity to be equal to the maximum value (c), results in a case in which the star approaches a black hole. The parameter ξ for black holes is then obtained as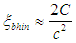 | (34) |
By computing ξ for the surface of the star along the equator and that of the star becoming a black hole using (34) will indicate where the singularity of the star lies (internal space breaking).Now, in similar manner, the gravitational velocity of the interior metric can be deduced as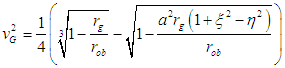 | (35) |
Setting the gravitational velocity equivalent to the maximum value (c), the parameter ξ for a black hole along the equator is obtained as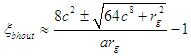 | (36) |
Using equation (36), the external space breaking can be obtained.Now, liquid oblate spheroidal stars can also be classified based on the star’s position of the space breaking in the gravitational field relative to its physical surface parameter.a) Regular oblate spheroidal stars: For this, the collapsed core or parameter ξbhout for a black hole of a regular star as in equation (34) is far smaller than the surface parameter ξ i.e ξbhin << ξbhout .Also, the space breaking as in equation (36) is found a distance away from the star (in the cosmos).b) Neutron Stars and Pulsars: In this case, the physical radius is very close to the collapsed core. If they are equal, the star cannot be observed as it will become invisible, thus, ξbhin ≤ ξsur face. The outer space breaking is located in the outer cosmos.c) Black Holes: In this case, the two space breaking parameters, inner (34) and outer (36) meet each other at the surface of the star. i.e. ξbhin=ξsurf ace=ξbhout.
4. Conclusions
The general relativity liquid star model provides the necessary theoretical and mathematical foundation needed to explore the Physics of liquid stars [20]. The theoretical analysis of the motion of particles/photons and gravitational phenomena inside and in the vicinity of stars can now be conveniently investigated. Oblate spheroidal liquid star model takes into account the precise shape of the Sun and other common stars. The novel classification of stars in this model is remarkable. Oblate spheroidal stars are classified into three groups (regular stars, neutron stars and black holes). The foundation established in this article therefore serves as a bridge for the verification of small departures of theory from reality in astronomy and astrophysics. Other gravitational phenomena in the vicinity of oblate spheroidal plasma stars can be studied with our metric tensor.
References
| [1] | Borrisova L. and D. Rabounski; Inside Stars, Rehoboth, New Mexico, 2014. |
| [2] | Eddington A. S. The Internal Constitution of the Stars. Cambridge University Press, Cambridge, 1926. |
| [3] | Kozyrev N.A. Sources of stellar energy and the theory of the internal constitution of stars. Part I. Proceedings of Crimean Astronomical Observatory, 1948, vol. 2, 3-43; Part II, ibid., 1951, vol. 6, 54-83 (in Russian). Published in English: Progress in Physics, 2005, issue 3, 61-99. |
| [4] | Robitaille P.-M. A high temperature liquid plasma model of the Sun. Progress in Physics, 2007, issue 1, 70-81. |
| [5] | Robitaille P.-M. A thermodynamic history of the solar constitution I: the journey to a gaseous sun. Progress in Physics, 2011, issue 3, 3–25. |
| [6] | Jeans J.H. Recent developments of cosmical physics. Nature, 4 December 1926, vol. 118, no. 2979, 29–40 (in the Supplement to the issue). |
| [7] | Robitaille P.M. A thermodynamic history of the solar constitution II: the theory of a gaseous sun and Jeans’ failed liquid alternative. Progress in Physics, 2011, issue 3, 41–59. |
| [8] | Borissova L. The gravitational field of a condensed matter model of the Sun: the space breaking meets the Asteroid strip. The Abraham Zelmanov Journal, 2009, vol. 2, 224–260. |
| [9] | Borissova L. De Sitter bubble as a model of the observable Universe. The Abraham Zelmanov Journal, 2010, vol. 3, 3–24. |
| [10] | Borissova L. The Solar System according to General Relativity: the Sun’s space breaking meets the Asteroid strip. Progress in Physics, 2010, issue 2, 43–47. |
| [11] | Borissova L. and Rabounski D. Fields, Vacuum, and the Mirror Universe. Svenska fysikarkivet, Stockholm, 2009. American Research Press, Rehoboth (NM, USA), 2010. |
| [12] | Darin R. Calculate the Shapes of Neutron Star Cores, www.zombal.com. |
| [13] | Dali K., Keke Z. and Gerald S. An exact solution for arbitrarily rotating gaseous polytropes with index unity. Monthly Notices of the Royal Astronomical Society 2015, vol. 448, 456-463. |
| [14] | Keke Z., Kit H. C. and Xinhao L. On precessing flow in an oblate spheroid of arbitrary eccentricity. |
| [15] | Laurent G., Takashi S., Masao T., Donald W. K., Hiromoto S., Michael B., Othman B., Aaron C. B. and Katepalli R. S. Shape of a slowly rotating star measured by asteroseismology. Science Advances 2016: Vol. 2, no. 11. |
| [16] | Anne M. H., Robert E. C. and Everett M. C. Verified solutions for the gravitational attraction to an oblate spheroid: Implications for planet mass and satellite orbits, Planetary and Space Science 2017: 1–14. |
| [17] | Chifu, E.N., Usman, A. and Meludu, O.C. Orbits in Homogeneous Oblate Spheroidal Gravitational Space Time. Progress in Physics, 2009 3, 49-53. |
| [18] | Chifu, E.N., Usman, A. and Meludu O.C. Gravitational Spectral Shift Exterior to the Sun, Earth and the Other Oblate Spheroidal Planets. Progress in Physics, 2010 4, 56-60. |
| [19] | Chifu E.N, A. Usman and O.C Meludu; “Gravitational Scalar Potential Values Exterior to the Sun and Planets”, Pacific Journal of Science and Technology 2009, 10(1): 663-673. |
| [20] | Chifu E. Ndikilar, Amusa S. Kolawole and Hafeez Y. Hafeez; Motion of Stellar Particles and Photons within Spherical Liquid Star, Indian Journal of Science and Technology, 2018: Vol 11(33). |


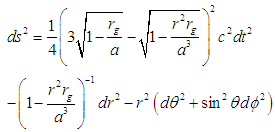
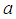 is the physical radius of the sphere,
is the physical radius of the sphere, 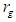 is the Hilbert radius of the astrophysical body given as
is the Hilbert radius of the astrophysical body given as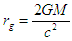 with
with 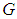 as the gravitational constant and
as the gravitational constant and 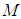 its mass. If the radial distance
its mass. If the radial distance 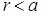 , then the metric describes the interior of the sphere of incompressible fluid. At the surface, we have
, then the metric describes the interior of the sphere of incompressible fluid. At the surface, we have 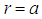 which makes the metric to coincide with that of a mass point. Also, the outer metric is the same as that of the mass point.Components (covariant and contravariant) of the gravitational inertial force are obtained by substituting the differential of the gravitational potential with respect to the coordinates into the gravitational force formula [1]. This gives:
which makes the metric to coincide with that of a mass point. Also, the outer metric is the same as that of the mass point.Components (covariant and contravariant) of the gravitational inertial force are obtained by substituting the differential of the gravitational potential with respect to the coordinates into the gravitational force formula [1]. This gives: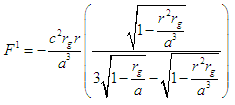
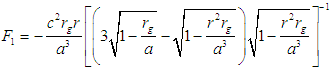
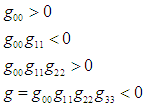
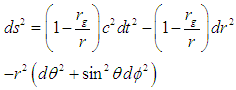
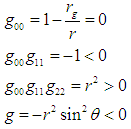
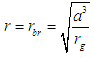
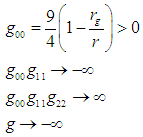

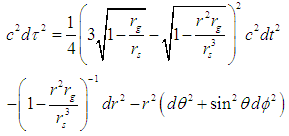
 is the radius of the spherical liquid star and
is the radius of the spherical liquid star and  is the proper time.Now, using deformation, the spherical liquid star can be transformed to take the shape of an oblate spheroidal liquid star. Suppose, the deformation is such that the mass Mo and density ρo of the star remain unchanged. Then, its surface parameter expressed in the oblate spheroidal coordinates system is [17, 18] as
is the proper time.Now, using deformation, the spherical liquid star can be transformed to take the shape of an oblate spheroidal liquid star. Suppose, the deformation is such that the mass Mo and density ρo of the star remain unchanged. Then, its surface parameter expressed in the oblate spheroidal coordinates system is [17, 18] as
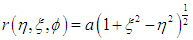
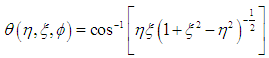
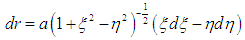
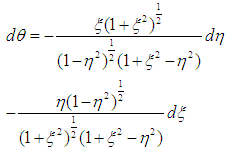
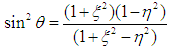
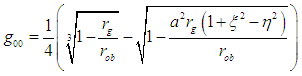
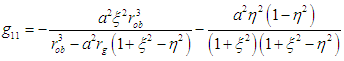
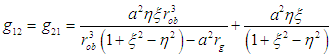
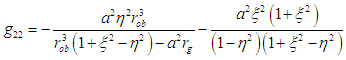
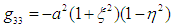
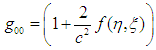
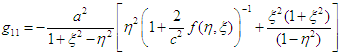
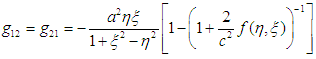
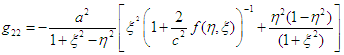
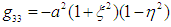
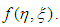 Now, space breaking due to the internal and external metric can be investigated according to the signature prescription given in equation (4).For the external field, the line element is
Now, space breaking due to the internal and external metric can be investigated according to the signature prescription given in equation (4).For the external field, the line element is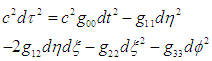
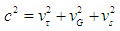
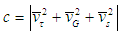
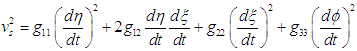
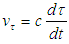
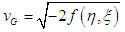
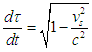
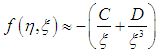
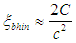
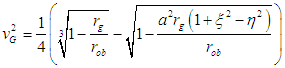
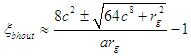
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML