-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Astronomy
p-ISSN: 2169-8848 e-ISSN: 2169-8856
2018; 7(1): 19-23
doi:10.5923/j.astronomy.20180701.03

An Action-Reaction Interpretation of the Interaction between Cosmic Expansion and Gravitation
Thomas A. Kriz1, Adam T. Kriz2
1Advanced Studies, Alpha Omega Research Foundation, Cedar Park, TX, USA
2Associate Member, Advanced Studies, Alpha Omega Research Foundation
Correspondence to: Thomas A. Kriz, Advanced Studies, Alpha Omega Research Foundation, Cedar Park, TX, USA.
| Email: |  |
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

An updated review is presented to demonstrate the impact an expanding cosmos on three approaches to analyzing gravity. 1) the General Relativity based tensor method, 2) the Escape Velocity based conservation of energy method, and 3) the Force-Balanced based action-reaction method. The only common solution from all three methods is a flat space result with critical matter density ρc=3H2/8πG where H is the Hubble parameter, and G is the gravitational constant. It is also shown that the use of a Force-Balance based analysis for action-reaction, derived from a conservation of energy baseline, is analytically equivalent to that of a General Relativity tensor-based analysis for a flat space solution. Galaxy-based energy conservation and force-balanced solutions in an expanding cosmos also indicate that cosmic expansion is the unique action-based cause of a gravitational reaction at a galaxy level. Friedmann solutions from General Relativity for open and closed space curvature, however, add a speed of light term to H that violates galaxy-based conservation of energy and action-reaction force balance requirements. Thus, such curved space solutions are not physically relevant in an expanding cosmos. Evidence from Guth-Linde Inflationary Universe models is also cited to support the validity of a unique galaxy-based flat space solution.
Keywords: Gravity, Action-reaction, Newton's third law, Cosmic expansion, General Relativity, Escape velocity
Cite this paper: Thomas A. Kriz, Adam T. Kriz, An Action-Reaction Interpretation of the Interaction between Cosmic Expansion and Gravitation, International Journal of Astronomy, Vol. 7 No. 1, 2018, pp. 19-23. doi: 10.5923/j.astronomy.20180701.03.
Article Outline
1. Introduction
- Traditionally, throughout human history, gravity has been seen as a natural attractive force between matter-based objects as a function of composition, size, shape, weight, and position. Physically speaking though, it is the weakest of the known forces, with about 10-38 times less strength than the “strong force” that binds the nucleus of atoms together. [1] The first reliable mathematical description of its attractive strength was defined by Issac Newton' in his 1687 “Principia” document, [2] where its attractive force was characterized as a product of the mass content of the two objects times a gravitational “constant” G, and divided by the inverse square of the distance between the objects. It can be seen, however, that although the Newton inverse square formula does not provide a clear causal basis for gravity, it does imply that the true cause of gravity is probably something that is proportional to mass of the objects. An accurate solution to gravitational attraction between objects, however, requires use of a gravitational field map that can be analyzed to obtain potential magnitude information that defines an accurate force result. At Newton's time, however, no such concept was known, so the impact of such map defined information was largely absorbed into the gravitational “constant” G. Such an analytical field map method would not be developed until the early 20th century. [3] It is now known that the value of the so-called “constant G” in Newton's inverse square formula actually changes with distance in the formula, especially at very short distances, but this could not be accurately measured in 1687. However, note also that, at far-field distances between objects, the Newtonian formula is remarkably accurate. [4]The General Relativity paper by Einstein in 1915, [5, 6] did, however, make use of a mathematical field map analysis method that demonstrated how an observer's view of space and time was affected by a gravitational field, and gave an entirely new perspective on how gravity could impact the observed geometry of a matter object. For example, a planet in orbit around the sun, could actually be viewed as falling gravitationally. It also showed that the Newtonian formula was only accurate as a “far field” limit on a gravitational field. However, General Relativity was also matter mass based, and therefore also failed to define a clear causal basis for gravity, the same as the Newtonian formula. Accurate field mapping analysis techniques in general were first developed early in the Twentieth century. The initial forms were graphical, such as those developed to provide electromagnetic graphical field solutions to Maxwell's Equations to aid in the design of electrical machinery in 1915 by Douglas. [7] Einstein's General Relativity in the same year made a giant leap forward, in that, in place of a graph, it actually made use of a mathematical model, based upon the Riemannian Geometry, that was equivalent to a set of ten simultaneous non-linear partial differential equations, which were used to obtain metric tensor solutions for gravity in a space-time geometry. [8] A similar mathematical approach to obtain the easier linear solutions to Maxwell's Equation set were not developed until almost 20 years later (around 1935), to support the design of RADAR systems. [9] However, as shown in the text by Ohanian and Ruffini, [10] it is also possible to develop a linear approximation of the General Relativity equation as an analog to Maxwell's Equations to get a simpler, more solvable model for some gravity problems. The usual approach to solving a field system of partial differential equations generally involves defining the governing equation set along with boundary conditions, and then pursuing a “guess and check” process to obtain solutions. [11] In such a case, there generally is no substitute for a good guess. When the General Relativity equation is used as the governing equation set, however, such a process is very complex. Thus, only about a half- dozen physically relevant solutions have been found during the last hundred years. [12] The process can be much simplified, however, if Special Relativity is used as a constraint condition when doing tensor-based analysis. [13] As shown in the text by Ohanian and Ruffini, there is no relativity principle which is more general than Special Relativity. [14] Thus, Einstein's General Relativity is actually subservient to Special Relativity, in this regard.
2. General Relativity Tensor Analysis Method
- Before the development of the 100” telescope on Mount Washington, observations in astronomy were limited to views inside the Milky Way galaxy, which internally appeared to have a near-static form. In 1929, use of the) 100” telescope, however, allowed astronomers to observe the expanding cosmos beyond the Milky Way. The question then is: How does the Milky Way galaxy avoid the impact of the cosmic expansion dynamic internally to have a local galaxy-based environment that seems equivalent to a near-static condition? The obvious response is that the mass of each galaxy is sufficiently large for its gravitation to balance the outward pull of cosmic expansion. Before the discovery of the expanding cosmos in 1929 by Hubble [15] using the Mount Washington telescope, a primitive General Relativity model for the cosmos had already been developed. In 1922-1924, a Russian living in St. Petersburg named Alexander Friedmann [16, 17] was able to solve the Einstein General Relativity field equation assuming a simplified model of the cosmos. The Friedmann model presumes a near-static form of the cosmos, commonly accepted at the time, and Einstein’s General Relativity equation, defined here in cgs units as [18]
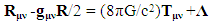 | (1) |
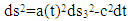 | (2) |
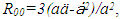 [19] and that Tμν equals matter density ρ in a perfect fluid-filled cosmos as a function of cosmic mass and volume, the form defined in (1) for the Friedmann model can then be reduced to two independent equations, one for cosmic space expansion and a second for acceleration-based space changes as a function of the curvature attribute
[19] and that Tμν equals matter density ρ in a perfect fluid-filled cosmos as a function of cosmic mass and volume, the form defined in (1) for the Friedmann model can then be reduced to two independent equations, one for cosmic space expansion and a second for acceleration-based space changes as a function of the curvature attribute 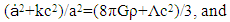 | (3) |
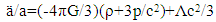 | (4) |
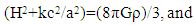 | (5) |
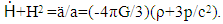 | (6) |
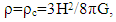 | (7) |
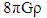 in (3) and (5) indicates that total cosmic rest mass is a constant, and uniformly distributed, implying that the cosmos in the Friedmann model can be interpreted as having only one galaxy (eg; the Milky Way) in which matter is presumed to always have existed. It can be seen that the term
in (3) and (5) indicates that total cosmic rest mass is a constant, and uniformly distributed, implying that the cosmos in the Friedmann model can be interpreted as having only one galaxy (eg; the Milky Way) in which matter is presumed to always have existed. It can be seen that the term 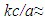 (3x108m/s per million light-yrs) in (3) and (5) is equivalent to adding a speed of light change to the value of H, which is questionable even in a near static model of the cosmos because of Special Relativity constraints. In this regard, however, note that current measurements for H show that a reasonable value in an expanding cosmos is approximately 17 km/s per million light-years. [20, 21] Theoretically, such a speed of light change to H in an expanding cosmos can only occur during an ideal radiation dominated phase when there is no gravity. It will be shown in the following that such curved space solutions also violate galaxy-based conservation of energy and action-reaction force balance requirements in an expanding cosmos.
(3x108m/s per million light-yrs) in (3) and (5) is equivalent to adding a speed of light change to the value of H, which is questionable even in a near static model of the cosmos because of Special Relativity constraints. In this regard, however, note that current measurements for H show that a reasonable value in an expanding cosmos is approximately 17 km/s per million light-years. [20, 21] Theoretically, such a speed of light change to H in an expanding cosmos can only occur during an ideal radiation dominated phase when there is no gravity. It will be shown in the following that such curved space solutions also violate galaxy-based conservation of energy and action-reaction force balance requirements in an expanding cosmos. 3. A Conservation of Energy based Escape Velocity Analysis Method
- Alternatively, a simpler energy-based solution for the relation between cosmic expansion and gravity in an expanding cosmos can be found in the texts by Beiser. [20, 21], and Tipler and Llewellen [22]. The method makes use of a galaxy-based escape velocity analysis approach that can be associated with cosmic expansion rate. Within the context of an expanding cosmos, the interaction between such expansion and gravity at each galaxy, therefore, is presumed to have an energy balanced form. Mathematically then, the energy balance for the interaction of cosmic expansion with gravity at a galaxy can be defined as
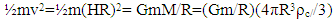 | (8) |
4. Newton's Third Law of Action-Reaction
- Since energy can be represented as a force through a distance, the implied force on the galaxy due to cosmic expansion and the force of gravity implied by energy equation (8) then can be defined as
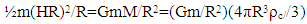 | (9) |
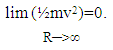 | (10) |
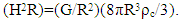 | (11) |
5. An Inflation based Evolutionary Scenario
- The scenario described here begins with an electromagnetic energy focused process described in another paper published by the Alpha Omega group. [23] Such an inflation-like event is natural and needs no artificially defined form, but still yields the same inflationary impact as those found in the Guth and Linde Inflationary models. [24] Initial conditions for the event assume that radiation wavelength at start is proportional to Planck Time (eg; λ∝10-45s), and initiates a radiation dominated phase that has no matter and thereby expands at light speed. At time proportional to ~1013 seconds, the radiation dominated phase ends with radiation wavelength of λ∝10-15s, thereby completing the Inflation-like process, and is followed by a three-stage decoupling event that initiates a matter dominated phase that is in accord with observed data from particle collision experiments. It should be noted that this decoupling time event at ~1013 seconds at this point is also consistent with that found in Inflationary models. The start of the matter dominated phase then sets the stage for the balanced condition between the positive energy cosmic expansion process and the negative energy gravitation process described in (8) and the force balanced activity defined by (9). Cosmic expansion continues until the conditions define in (10) are satisfied when both cosmic expansion and gravitation no longer exist. If Newton's Third law must always be true during the matter dominated phase in order to conserve energy, the processes in (8) and (9) involving cosmic expansion and gravitation continue until satisfying the condition defined in (10). Thus, cosmic expansion and gravitation can therefore only reach a null condition simultaneously. The open space (eg; with k=+1, ρ<ρc) and closed space (eg; with k=-1, ρ>ρc) solutions to (3) and (5) developed by Friedmann, however, add a speed of light term to H, and thereby fail to satisfy both action-reaction force as well as conservation of energy requirements. What happens when cosmic expansion stops and gravity fails? Stars, planets, galaxies, black holes, and other material objects come completely apart, and solar-like system structures no longer exist. According to Equation (10), this occurs well after star, galaxy, and solar system formation have long ceased to exist. All stars have long ago reached old age and emit no radiation. Only a dark and cold cosmos remains full of primitive matter. Newton's Third law may still remain, but without serious impact.
6. Conclusions
- It is shown in the foregoing that the force balance between cosmic expansion and gravitation, though different in process form, uniquely satisfies Newton's Third law with a flat space density solution of ρ=ρc=3H2/8πG. Such a flat space geometry expands forever with an expansion rate that continues to become ever smaller. Indeed, in the vast majority of cases, both the action and reaction components involving Newton's Third law do have the same energy process form, but, note that the important part of the law is the requirement that forces be balanced. It also can be seen then, in the case of cosmic expansion as an action-based force, there is no equal and opposite balancing reaction force other than that from gravitation. It is also shown that a galaxy-based action-reaction force-balanced analysis is equivalent to a General Relativity analysis procedure with k=0 for a flat space solution. When using a Friedmann based open space-time k=+1 (with ρ<ρc ) solution, or the closed space-time k=-1 (with ρ>ρc ) solution, however, a speed of light term is added to the Hubble parameter H that violates galaxy-based requirements for conservation of energy and action-reaction force balance in an expanding cosmos. It should also be noted that cosmic expansion is a positive energy action form and that gravitation is a negative energy reaction form. Thus, the sum of both together, per Newton's Third law, yields a net null energy condition. Both together then also constitute a necessary condition set for the existence of gravity. A corollary result to the irrelevance of a closed space solution during cosmic expansion is that a BIG CRUNCH cosmic collapse is unlikely. If ρ=ρc uniquely, a reversal of outward cosmic expansion can never occur. It should be noted the results given here are also consistent with those from cosmic Inflationary models. [24, 25] As long as Inflation continues long enough, the state of space-time in the cosmos, viewed as an expanding 3-sphere in 4-sapce, is driven toward a flat space-time condition. [25] Similarly, in terms of a 2-sphere balloon model, as the balloon continues to be inflated, the flatter its surface becomes. Thus, Inflationary models generally lead to a ρ=ρc flat space solution. As an alternative to the Guth and Linde Inflationary models, a more natural, Inflation-like model discussed above, is one which begins with initial photon wavelength proportional to Planck Time (λ10-45s). This initial surge of energy is followed by a matter free radiation dominated phase expanding at the speed of light for ~1013 seconds that ends with λ10-15s at the beginning of a matter dominated phase, same as in the Guth and Linde models. Thereby, the overall inflationary impact (eg; 1030) is also the same as that found in traditional Inflationary models. It should be noted that some observations on type 1a supernovae [26] appear to give evidence of late era acceleration in the cosmic expansion rate, following the matter dominated era discussed here. There is currently ongoing study to learn more about a possible interaction.
ACKNOWLEDGEMENTS
- The authors wish to express gratitude for the encouragement and critical review received during the earlier stages of the work present here received from E.J. Bacinich, Director of the Alpha Omega Research Foundation, and other members of our group, now deceased: Prof. Behram Kursunoglu and Dr. Walter Rosenthal. Prof. Kursunoglu was the Director of the Theoretical Institute at the University of Miami (FL), and pursued graduate studies at Cambridge University under P.A.M. Dirac. Dr. Walter Rosenthal was one of the last students to pursue graduate studies in physics at the University of Berlin under Max Planck.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML