-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Astronomy
p-ISSN: 2169-8848 e-ISSN: 2169-8856
2018; 7(1): 6-18
doi:10.5923/j.astronomy.20180701.02

The Theory about Light
J. W. Vegt
Technical University Eindhoven, The Netherlands
Correspondence to: J. W. Vegt, Technical University Eindhoven, The Netherlands.
| Email: |  |
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

A change in approach in the theory of Relativistic Electromagnetic Fields, introduced by James Clerk Maxwell in 1865 and the theory of “Electric-Magnetic / Space-Time” conversions by Einstein-Lorentz-Minkovski in 1905 in the theory of Special Relativity (specially described by the Lorentz-Transformations) and the Theory of General Relativity (GTR) by Albert Einstein in 1915 has been presented in this article. What is known in Astrophysics has originally been based on the fundamental knowledge of the classical Electromagnetic theories of James Clerk Maxwell and the famous Theory of General Relativity by Albert Einstein. Electromagnetic radiation and in specific light has always been the carrier for this information. That is a fundamental problem. Because what do we really know about light? When James Maxwell published his famous set of 4 electromagnetic equations, the Maxwell equations, he did not built his theory on a logical fundament. His foundation was not logical at all. Why would a set of 4 electromagnetic equations which are correct at low frequencies describe a physical phenomenon like the propagation of light with a speed that at that time had never been measured before? Since then nobody ever doubted about the correctness of the theories of Maxwell. The success of his predictions made Maxwell famous. But fame is not a ground for fundamental science.
Keywords: General Relativity, Electromagnetic-Gravitational Interaction
Cite this paper: J. W. Vegt, The Theory about Light, International Journal of Astronomy, Vol. 7 No. 1, 2018, pp. 6-18. doi: 10.5923/j.astronomy.20180701.02.
Article Outline
1. Introduction
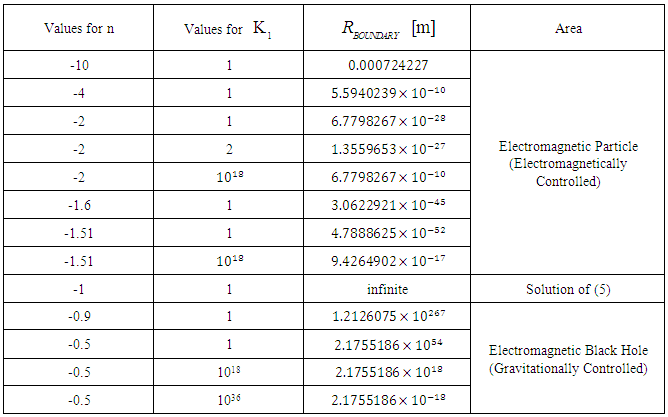
- The famous eclipse expedition of 1919 to Sobral, Brazil, and the island of Principe, in the Gulf of Guinea, led by Dyson, Eddington and Davidson was a turning point in the acceptance of the General Theory of Relativity developed by Albert Einstein in 1915. The correctness of this theory has been proven since then in many experiments. The success of his predictions made Einstein famous. But fame is not a ground for real science. Because what do we really know about light? When Albert Einstein published his famous Einstein Field Equations (Einstein-Maxwell equations), which were the mathematical foundation on which the Theory of General Relativity has been built, he did not built his theory on a logical fundament. Einstein built his theory on the complex 4-dimensional Minkovski Space, developed by Hermann Minkovski, the Electromagnetic Lorentz Transformations, developed by Hendrik Antoon Lorentz and the fundamental Maxwell Equations. His foundation was not logical at all but grounded on the success of those who became famous before him. But fame is never a ground for fundamental science. Einstein had a great imagination and was inspired by the imaginary 4-dimensional complex space-time continuum, suggested by his teacher Hermann Minkovski. But his foundation was not logical at all. Why would space and time be equal. We do experience space and time always very differently. When we shine the light into a room, all three spatial dimensions of the room will be enlightened and become visible. But the fourth dimension time will always remain invisible. We cannot look into the future and we cannot look back in time by the illumination of light that shines into time. There is no logical ground for the Theory of General Relativity. Since the success of the predictions of Albert Einstein, nobody ever doubted about the correctness of the theories of Albert Einstein. The success of his predictions made Einstein famous.In this manuscript, the starting point is almost 300 years ago. Long before James Maxwell published his Maxwell equations, before Albert Einstein published the Theory of General Relativity and far before the time Niels Bohr introduced the probability waves, discovered by Erwin Schrödinger which were the nonlogical grounds on which Quantum Physics has been built.The starting point is the moment just after Isaac Newton had published the breaking of light into the colors of the rainbow through a prism in the Lectiones Opticae” in 1728. Newton just had discovered the beauty of light when light had revealed one of its many secrets. And he could only express: “Light is beautiful”. That has been the turning point in our history of science. Since then science has left the path of the light and has followed the path of our own mind. We did not follow anymore, but we started to lead. To lead in arrogance and surrounded by the illusions of fame. But instead of following the path of the mind that has left every logical thinking, a path that is finally following the path of quantum physics and elementary particles, the ghost lights that will lead us to the swamps of darkness, this manuscript wants to return to the path of the light. Because the light has always given the right answers. And has always guided mankind in science and through life. What would our world be without the beauty of light? When we look at the fruits of our modern science we can only see the fruits of darkness. A darkness where the predators are hiding to destroy our world of beauty, our world of light, our world of truth. Who are we following? The gambling devil leading us towards the ghost lights, the elementary particles, our new religion, which will finally lead us into the swamps of darkness, the swamps of blindness and finally no scientist will know how to go further? Or do we follow the fake light of the illusion of fame that will lead us into the deepest darkness the world has ever known? In this time where a totally destructive final world crisis is building, the world needs leadership. And the most powerful leadership is science. But how can science lead when science is totally blind. And science believes in the lies of the illusions of Maya. We behave like children who throw a clock towards the wall until it falls apart and the wheels fall on the ground. Yes, a child believes that then it understands how a clock works. But that is the fantasy of a child. Like we believe that we will understand matter by smashing matter in high energy accelerators until it breaks apart into elementary particles. But that is the science of a child. A world of fantasy where logic does not exist. Because a clock is so much more than a collection of wheels. To understand a clock we have to build a clock. To understand matter we have to build matter. And we will never be able to build matter until we understand the secrets of light.Science needs a compass like a ship needs a compass. A compass without a ship sinks to the bottom of the ocean and will be totally meaningless. A ship without a compass will finally destroy itself when it breaks on the rocks of arrogance like the Titanic broke itself in arrogance. The ship needs the compass and the compass needs the ship. Together they are powerful. Alone they will destroy themselves. The science in our world is a science blind without a heart. The religion in our world is a non-logical religion without a mind. The heart needs the mind and the mind needs the heart. Together they are the most powerful weapon in spiritual warfare and together they can save the world and destroy the powers of darkness that are coming to the world. Alone they have no chance to survive the powers of evil and the world will come to an end surrounded by darkness. A worldwide holocaust, the world has never seen before. The empire of evil. Only when religion and science come together, they will become invincible and the evil powers will break themselves on this invincible shield. A shield that will rise when the heart and the mind come together. Because science alone will be fooled by the darkness, because the science is blind and cannot see when it is surrounded by the darkness. In blindness science has created the atomic bombs that has destroyed Hiroshima and Nagasaki, in blindness science creates the most evil missiles and warplanes to kill and burn alive innocent women and children, in blindness sciences creates drones that are designed only to kill and bring fear over the world, in blindness science designs data systems that will control mankind and bring them to slavery, in blindness science creates genetical manipulation to destroy who we really are, in blindness science serves the darkness. And religion alone will also be fooled by the darkness, because religion is blind and has lost any logical way of thinking when it is surrounded by the darkness. In blindness religion has burned innocent people alive on the stakes in the middle ages, in blindness religion has created wars and has killed so many innocent victims, in blindness religion has broken the souls of those who were different and did not fit into its own small and limited boundaries, in blindness religion has broken the people who believed in a different God, in blindness religion has broken the soul of those with a different sexuality, in blindness religion has broken to most beautiful and the most valuable people in our world, in blindness religion serves the darkness. Religion has lost its mind when it has forgotten the revelation of God when God revealed himself to Moses from the midst of the burning bush by his only true name “YHWH”. “I am who I am”. And that is the only logical consequence in religion. We have to be who we really are in the deepest of our soul and we have to let the other be who he or she really is. Do not transform ourselves or the others but follow the name of YHWH and be who you really are and let the other be who he or she really is. Instead of judging and breaking people because of their sexuality, those who are gay, transgender, pansexual, intersexual and so many other sexualities. Let them be who they are in the name of YHWH and do not judge them. What other kind of religion or God people do believe in, let them be in the name of YHWH, do not judge them. Respect who they are and what they do believe in. That is the only logical consequence of the holy name “YHWH”. Evil grows on the fields of pain, injustice and suffering. And evil will cause more pain, more injustice and more suffering so that more evil will grow. Until evil will finally cover the whole earth and the evil will kill all the light, all the hope and all the love. Evils grows like a weed and feeds itself from the life forces of those who are strong and healthy until they are destroyed and the hope and the love in them has died.Evil grows like it has grown in the concentration camps of evil in Auschwitz-Birkenau, Treblinka, Sobibor and so many concentration camps in the second world war where the injustice ruled and the hope and the love were killed. That is the face of darkness. That is the face of evil. That is our future when we do not fight back. Jesus gave mankind the perfect weapon to destroy the evil, to destroy the darkness. “Love your enemies”. These are his powerful words in spiritual warfare. Because by loving our enemies we will destroy them. We will smash the darkness that has taken them into the bright light of love. Only by love we will destroy the fields of pain on which the evil is growing, by love we will destroy the powers of injustice that gives power to the evil, by love we will bring back the hope because hope is the light the darkness cannot face. There is no power in the whole universe stronger than love. And only love can destroy darkness and only love can destroy evil and only love can save the world. All the Jews, all the Muslims and all the Christians in our whole beautiful world are following “YHWH”, the only creator of the universe, the only creator of the light. God of truth, God of justice, God of mercy. But who are you following? “YHWH” is his only name, “I am who I am”. You can only follow “YHWH” by being “YHWH”. Be who you really are and do not let yourself be threatened by fear and be enslaved by the king of darkness. When you are rainbow color sexual, be rainbow color sexual. The love has no walls. The love has no boundaries. The love has no fear. The love is pure and is created by “YHWH like he created the light and the beauty of the light shines through the rainbow. The only one who want to be kneeled for is the king of darkness. The only one who wants to enslave the whole world in his darkness is the king of darkness. The only one who preaches the fear is the king of darkness. The only one who kills the beautiful love in the human soul is the king of darkness. Why are you following the king of darkness with his evil lies, tricks and manipulations of truth. The king of darkness, he who has entered, hidden in darkness, your holy Synagogues, your holy Mosques and your holy Churches. In blindness you are preaching the fear. In blindness you are preaching the merciless judgement. In blindness you are preaching the war. In blindness you are serving the darkness. The king of darkness who has entered the holy Temple of Science. The Temple of the mind. The Temple of power, controlled by funding. You are managed, controlled and enslaved by money, controlled by evil. How could you forget your heart. Instead of using your power to save the people and to save the world, you use your power to create war machines to kill people, to create software that will finally be used to enslave the whole world and to manipulate the genetic code of our whole creation. You who believe in honor, in prizes, in funding are being mislead by honor, by funding and by prizes. You are creating the fruits of darkness and in blindness you are following the king of darkness. Mislead by non-existing probability. Mislead by non-existing elementary particles. Mislead by darkness. “YHWH” is the light. The light that will destroys the darkness and will save the world. The light that shines in this world and becomes visible in the spiritual world as love. When religion comes together with science, when the heart finds back the mind, evil will lose all his power. Then we will find that the light in our world is the same light that we see after we die. And in the spiritual world, the world we were before we were born, the world we go to after we die, in that world, love is visible as the strongest and the most beautiful light we have ever seen. Light is the first we see when we are born. Light is the first we see after we die. When we will understand the deepest secrets of light, the walls between our world and the spiritual world of the life after death will fall down. “YHWH”. I am who I am. When we become “YHWH” we will understand that we are the spiritual world as well as this world as well as the doorway to heaven. The father, the Son and the Holy Spirit. The Tri-Unity “YHWH”. We are the Tri-Unity of light as it was said by Jesus. Light is in the spiritual world (The father). Light is in this world (The son, born out of the Father, this world born out of the spiritual world). Light is the only doorway, the Holy Spirit, that connects this world with the spiritual world and let us pass from this world to the spiritual world when we die. As Jesus has spoken: “I am the light of the world (John 8:12). No one comes to the father than through the son (John 14:6). I am the doorway to heaven (John 10:9)”. Jesus spoke about the light when he spoke about the Father, the Son and the Holy Spirit. Only the light can bring back together science and religion. When science and religion come together, when the heart comes back to the mind, a shield will rise that no evil can pass.The doorway of light through which we leave this earth when we die and pass on from this world to the spiritual world. To heaven or to hell. Everyone who dies has to pass through the doorway of light, the Holy Spirit. An immense light that blinds you and throws you back. A light that only the love can pass.That is the new path for science and religion together. To find back the light, science has thrown away. To find back the cornerstone that the world has lost. In his famous conclusion to the book: “A Brief History of Time”, one of our most courageous scientists Stephen Hawking has written: “If scientists could find the most fundamental laws of nature, then we should know the mind of God”.When we return back to the world of light, we simply have to ask one question to the light. How is it possible that the light in our world does exist? And we simply follow Newtons third law of equilibrium published in the “Principia Mathematica Philisophiae Naturalis” in 1686. This single fundamental only question has been asked: What are the fundamental boundaries which are required for a stable electromagnetic field configuration in which light can exist? And instead of taking the 4 well-known electromagnetic low frequency equations and put them together and find exactly the same results as James Maxwell has found, a different path has been chosen. There is only one boundary condition. “The electromagnetic field has to be in a perfect equilibrium (balance) with itself and its surrounding.” And when an electromagnetic field interacts with a gravitational field, exactly the same boundary condition is required. That is the single and only requirement. From this single requirement follows one single equation. Equation (5) (gravity excluded) and equation (5-a) (gravity included) in this manuscript. All the solutions for electromagnetic configurations that are solutions of the Maxwell Equations are also solutions of Equation (5). But because of the special mathematical structure of (5) and (5-a) other electromagnetic field configurations are possible. And this will have an impact on our understanding of the universe, on our understanding of light. Because we cannot understand the universe until we understand light.John Archibald Wheeler [1] introduced in 1953 the concept of GEONS (Gravitational ElectrO-magnetic eNtities) in which electromagnetic radiation has been confined by its own gravitational field. To calculate the dimensions of these gravitational-electromagnetic confinements J. Wheeler based his calculations on the Einstein-Maxwell equations, the mathematical ground on which the Theory of General Relativity has been built and found electromagnetic-gravitational confinements with a diameter of several lightyears and a lifetime of several milliseconds. The results were very disappointing because an elementary particle with a diameter of several lightyears and a lifetime of a few milliseconds can hardly be considered as an elementary particle. In the presented theory the electromagnetic-gravitational interaction has been grounded on Newton’s third law. It has been grounded on the stability of electromagnetic-gravitational fields in a perfect equilibrium with itself and its surrounding. In table 1, electromagnetic-gravitational confinements have been presented for any harmonic (sinusoidal) frequency with an infinite lifetime and diameters varying from
 based on equation 5-a in a spherical coordinate system.Because this fundamental approach in electromagnetic field configurations is different than the classical approach by J. Maxwell and A. Einstein, a different result is expected. Instead of electromagnetic-gravitational confinements with a diameter of several lightyears and a lifetime of several milliseconds, presented by J. Wheeler in 1953, electromagnetic-gravitational confinements have been presented in Table 1 with diameters varying from
based on equation 5-a in a spherical coordinate system.Because this fundamental approach in electromagnetic field configurations is different than the classical approach by J. Maxwell and A. Einstein, a different result is expected. Instead of electromagnetic-gravitational confinements with a diameter of several lightyears and a lifetime of several milliseconds, presented by J. Wheeler in 1953, electromagnetic-gravitational confinements have been presented in Table 1 with diameters varying from 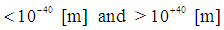 and an infinite lifetime for any harmonic frequency based on equation (5-a).
and an infinite lifetime for any harmonic frequency based on equation (5-a).2. The Dynamic Equilibrium Equation
- In a way comparable to the way that GEONS (Gravitational ElectrO-magnetic eNtities) are described by J. Wheeler in General Relativity by the Gravitational-Electromagnetic Equilibrium Equation [1, 7, 8, 13, 35, 38] (the Einstein-Maxwell Equations), Electromagnetic Confinements are described by the Dynamic Equilibrium Equation (5). The Maxwell tensor [9] equals:
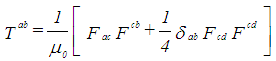 | (1) |
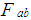 are the elements of the Maxwell tensor defined by:
are the elements of the Maxwell tensor defined by: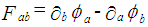 | (2) |
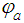 is defined by:
is defined by: 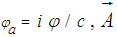 where
where 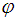 is the electric scalar potential, c the speed of light in vacuum and
is the electric scalar potential, c the speed of light in vacuum and 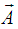 is the magnetic vector potential [1, 2, 3]. Substituting (2) in (1) results in the Energy Momentum Tensor [1, 16, 29]:
is the magnetic vector potential [1, 2, 3]. Substituting (2) in (1) results in the Energy Momentum Tensor [1, 16, 29]: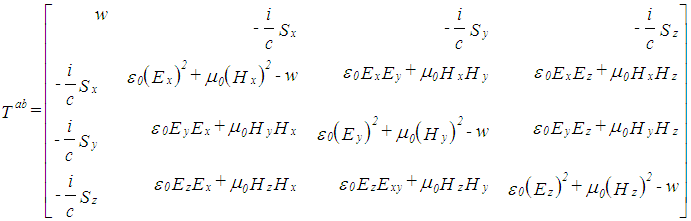 | (3) |
 in the 3 directions of the 3 coordinates of the chosen 3-coordinate system follows from the divergence of the electromagnetic energy-momentum [8, 9, 38] tensor (3). Equation (4) gives the 3-dimensional force density
in the 3 directions of the 3 coordinates of the chosen 3-coordinate system follows from the divergence of the electromagnetic energy-momentum [8, 9, 38] tensor (3). Equation (4) gives the 3-dimensional force density 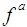 is a coordinate-free vector equation:
is a coordinate-free vector equation: | (4) |
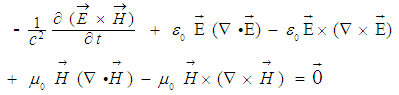 | (5) |
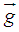 equals:
equals: 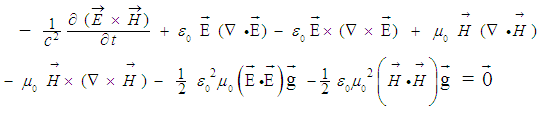 | (5a) |
2.1. EM Radiation within a Cartesian Coordinate System in the Absence of Gravity
- The required Electromagnetic Field Configuration for a perfect Equilibrium in Space and Time follows from the dynamic equilibrium equation (5) and equals in Cartesian Coordinates
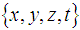 for the Electric Field Components e
for the Electric Field Components e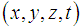 :
: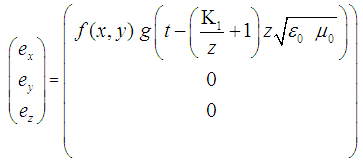 | (6) |
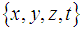 for the Magnetic Field Components m
for the Magnetic Field Components m :
: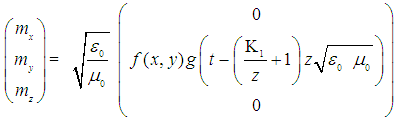 | (7) |
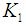 is an arbitrary constant. For the divergence-free function
is an arbitrary constant. For the divergence-free function 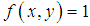 , the solutions (6) and (7) are also the solutions for the known Maxwell Equations. For the non-divergence-free functions
, the solutions (6) and (7) are also the solutions for the known Maxwell Equations. For the non-divergence-free functions 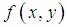 , the solutions (6) and (7) are not solutions for the Maxwell Equations, which requires divergence-free electromagnetic waves, propagating with the speed of light
, the solutions (6) and (7) are not solutions for the Maxwell Equations, which requires divergence-free electromagnetic waves, propagating with the speed of light 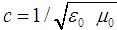 , in the absence of any matter. But they are solutions of the Dynamic Equilibrium Equation (5) and clearly do exist in physics. Comparable with the projection of a slide with a beamer on a flat screen in the z-direction. In which the slide has an arbitrary intensity-division
, in the absence of any matter. But they are solutions of the Dynamic Equilibrium Equation (5) and clearly do exist in physics. Comparable with the projection of a slide with a beamer on a flat screen in the z-direction. In which the slide has an arbitrary intensity-division 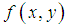 . The information
. The information 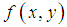 on the slide propagates with the speed of light
on the slide propagates with the speed of light 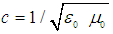 towards the screen in the z-direction in this example.
towards the screen in the z-direction in this example.2.2. EM Radiation within a Cartesian Coordinate System under the Influence of a Longitudinal Gravitational Field g
- The required Electromagnetic Field Configuration for a perfect Equilibrium in Space and Time for a Longitudinal Gravitational Field (The Light propagates in the same z-direction as the z-direction of the Gravitational Field) follows from the Dynamic Equilibrium Equation (5a) and equals in Cartesian Coordinates
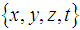 for a gravitational field “g” for the Electric Field Components e
for a gravitational field “g” for the Electric Field Components e  :
: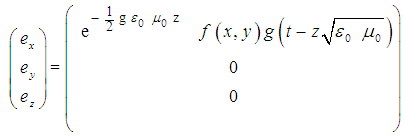 | (6a) |
 for a gravitational field “g” for the Magnetic Field Components m
for a gravitational field “g” for the Magnetic Field Components m :
: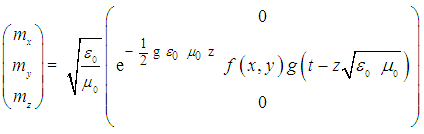 | (7a) |
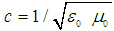 , independently of the strength g of the gravitational field in the z-direction. However, the amplitude of the electromagnetic wave becomes dependently of the gravitational intensity “g” and the distance “z” and changes along the z-axis with the electromagnetic-gravitational interaction term
, independently of the strength g of the gravitational field in the z-direction. However, the amplitude of the electromagnetic wave becomes dependently of the gravitational intensity “g” and the distance “z” and changes along the z-axis with the electromagnetic-gravitational interaction term 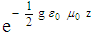 . In this example is chosen for e.g. a laser beam positioned vertically on the ground on earth, shining vertically against the gravitational field “g” of the earth. Because the laser beam presents electromagnetic energy, the beam has electromagnetic mass. The potential energy of the electromagnetic mass is increasing while the laser light is propagating upwards, against the direction of the gravitational field. Because of the law of conservation of Energy, the electromagnetic energy is decreasing over a distance “z” proportional with the same amount
. In this example is chosen for e.g. a laser beam positioned vertically on the ground on earth, shining vertically against the gravitational field “g” of the earth. Because the laser beam presents electromagnetic energy, the beam has electromagnetic mass. The potential energy of the electromagnetic mass is increasing while the laser light is propagating upwards, against the direction of the gravitational field. Because of the law of conservation of Energy, the electromagnetic energy is decreasing over a distance “z” proportional with the same amount 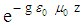 as the potential energy of the electromagnetic mass is increasing.
as the potential energy of the electromagnetic mass is increasing. 3. Electromagnetic Radiation within a Spherical Coordinate System
- The Spherical Coordinate System
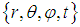 is parameterized by the radius r of the Sphere, the polar angle
is parameterized by the radius r of the Sphere, the polar angle 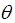 and the azimuthal angle
and the azimuthal angle 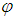 and the time t.
and the time t. 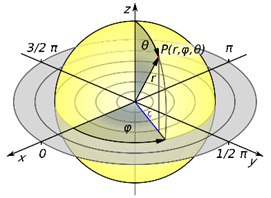 The required Electromagnetic Field Configuration for a perfect Equilibrium in Space and Time follows from equation (5) and equals in Spherical Coordinates
The required Electromagnetic Field Configuration for a perfect Equilibrium in Space and Time follows from equation (5) and equals in Spherical Coordinates 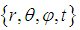 for the Electric Field Components e
for the Electric Field Components e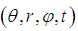 :
: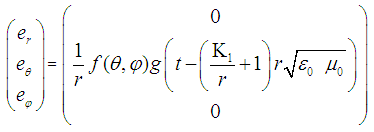 | (8) |
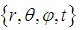 for the Magnetic Field Components m
for the Magnetic Field Components m :
: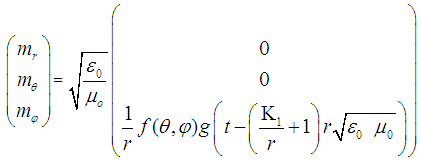 | (9) |
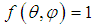 , the solutions (8) and (9) are also the solutions for the known Maxwell Equations. For the non-divergence-free functions
, the solutions (8) and (9) are also the solutions for the known Maxwell Equations. For the non-divergence-free functions 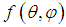 , the solutions (8) and (9) are no solutions for the Maxwell Equations, which require divergence-free electromagnetic waves in the absence of any matter. [29, 35, 36, 37, 38]. They are however solutions of the DEE (5) and clearly they do exist in physics. Like the radiation of an inhomogeneous point light source like a LED.
, the solutions (8) and (9) are no solutions for the Maxwell Equations, which require divergence-free electromagnetic waves in the absence of any matter. [29, 35, 36, 37, 38]. They are however solutions of the DEE (5) and clearly they do exist in physics. Like the radiation of an inhomogeneous point light source like a LED.4. Confined Electromagnetic Radiation within a Spherical Coordinate System through Electromagnetic-Gravitational Interaction
- In physics it has been in generally assumed that the speed of light
 is a physical constant. In this paragraph the possibilities will be discussed of a variable speed of light [10, 11, 12], that can vary from zero until values higher than c. The only requirement for the existence of an Electromagnetic Field Configuration will be the requirement of a perfect equilibrium in space-time for the chosen electromagnetic field configuration [13, 14, 15]. This single unique requirement will always be a solution of the DEE (5).The required Electromagnetic Field Configuration for a perfect Equilibrium in Space and Time [16, 17, 18, 30, 31, 39] in respectively the:
is a physical constant. In this paragraph the possibilities will be discussed of a variable speed of light [10, 11, 12], that can vary from zero until values higher than c. The only requirement for the existence of an Electromagnetic Field Configuration will be the requirement of a perfect equilibrium in space-time for the chosen electromagnetic field configuration [13, 14, 15]. This single unique requirement will always be a solution of the DEE (5).The required Electromagnetic Field Configuration for a perfect Equilibrium in Space and Time [16, 17, 18, 30, 31, 39] in respectively the: 
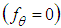 and the
and the 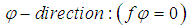 follows from equation (5). In Spherical Coordinates
follows from equation (5). In Spherical Coordinates 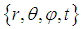 the solution for the DEE (5) for the Electric Field Components
the solution for the DEE (5) for the Electric Field Components 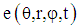 equals:
equals: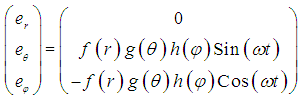 | (10) |
 the solution for the DEE (5) for the Magnetic Field Components
the solution for the DEE (5) for the Magnetic Field Components  in respectively the:
in respectively the: 
 and the
and the 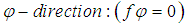 for the magnetic field components follows from equation (5) [29, 30, 31]. and equals:
for the magnetic field components follows from equation (5) [29, 30, 31]. and equals: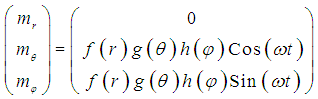 | (11) |
 of an Electro-Magnetic Field Configuration [19, 20, 21]. In a coordinate free vector equation. It follows from equation (4) that the radiation pressure in radial direction does not counterbalance and does not equal zero.
of an Electro-Magnetic Field Configuration [19, 20, 21]. In a coordinate free vector equation. It follows from equation (4) that the radiation pressure in radial direction does not counterbalance and does not equal zero. 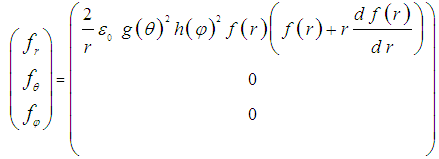 | (12) |
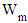 of the Electromagnetic Configuration is essential for the calculation of the inward bounded gravitational pressure. The electromagnetic field configuration (10) and (11) for the functions
of the Electromagnetic Configuration is essential for the calculation of the inward bounded gravitational pressure. The electromagnetic field configuration (10) and (11) for the functions 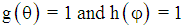 , results into the electromagnetic energy-density
, results into the electromagnetic energy-density 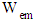 :
: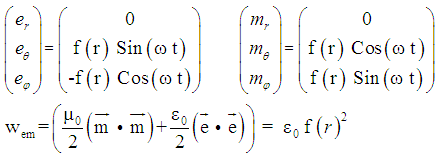 | (13) |
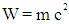 , the specific electromagnetic mass [22, 23, 24, 29]. Density
, the specific electromagnetic mass [22, 23, 24, 29]. Density 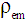 equals:
equals: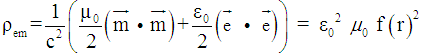 | (14) |
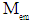 within a sphere with radius R equals:
within a sphere with radius R equals: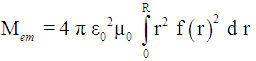 | (15) |
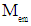 within the sphere [25, 26, 27, 30]. causes, according Newton’s Shell Theorem [28, 29, 30], a gravitational field strength
within the sphere [25, 26, 27, 30]. causes, according Newton’s Shell Theorem [28, 29, 30], a gravitational field strength 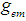 :
: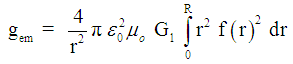 | (16) |
 is the gravitational constant and equals
is the gravitational constant and equals 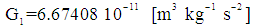 . The gravitational inwards bounded radiation pressure [29, 31, 32, 33] follows from (16):
. The gravitational inwards bounded radiation pressure [29, 31, 32, 33] follows from (16):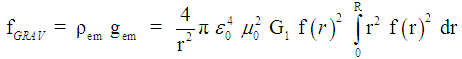 | (17) |
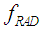 and the inward bounded gravitational pressure [29, 34, 35, 38, 39].
and the inward bounded gravitational pressure [29, 34, 35, 38, 39]. 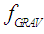 we find from (12) and (17) the radius of the boundary sphere of the enclosed radiation
we find from (12) and (17) the radius of the boundary sphere of the enclosed radiation 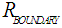 . For the functions
. For the functions 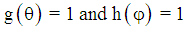 ,
, | (18) |
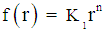 | (19) |
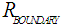 :
: | (20) |
 (2) at different values
(2) at different values 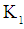 and n:
and n:
|
5. Confined Electromagnetic Radiation within a Toroidal Coordinate System
- The Toroidal Coordinate System
 is parameterized by the large radius R of the Torus. The Toroidal Coordinate System is obtained by rotating bipolar coordinates
is parameterized by the large radius R of the Torus. The Toroidal Coordinate System is obtained by rotating bipolar coordinates 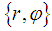 around an axis perpendicular to the axis connecting the two foci. The coordinate
around an axis perpendicular to the axis connecting the two foci. The coordinate 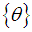 specifies the angle of rotation.
specifies the angle of rotation. 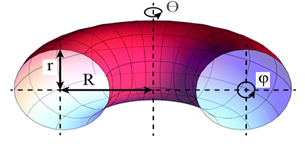 The Torus in the figure below has been constructed with a Radius R = 3 and r = 1.
The Torus in the figure below has been constructed with a Radius R = 3 and r = 1.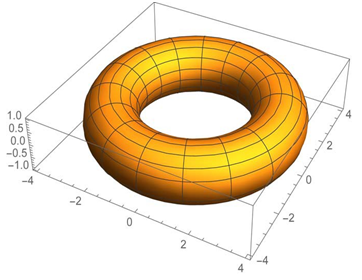 The required Electromagnetic Field Configuration for a perfect Equilibrium in Space and Time equals in Toroidal Coordinates
The required Electromagnetic Field Configuration for a perfect Equilibrium in Space and Time equals in Toroidal Coordinates 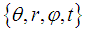 for the Electric Field Components e
for the Electric Field Components e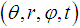 :
: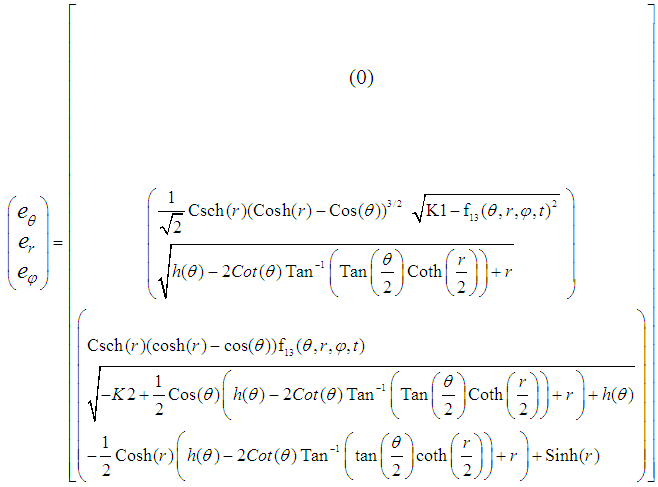 | (21) |
 for the Magnetic Field Components m
for the Magnetic Field Components m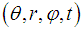 :
: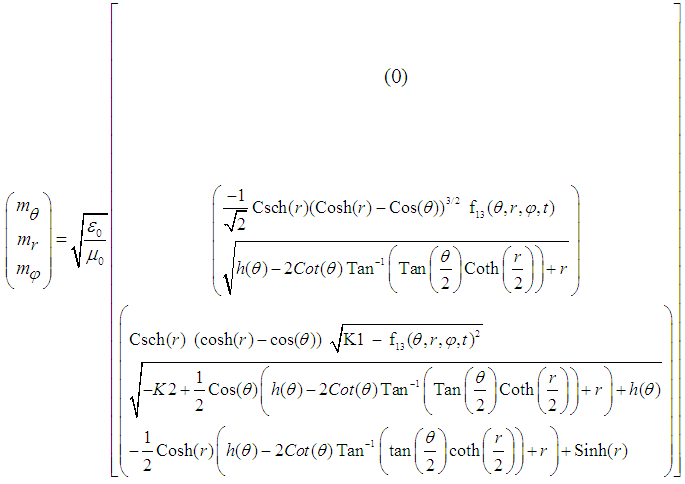 | (22) |
6. Confined Electromagnetic Radiation within a Toroidal Coordinate System through Electromagnetic-Gravitational Interaction in a non-linear Space-Time Continuum
- The required Electromagnetic Field Configuration for a Gravitational-Electromagnetic Equilibrium in Space and Time equals in Toroidal Coordinates
 for the Electric Field Components e
for the Electric Field Components e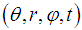 :
: | (23) |
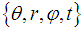 for the Magnetic Field Components m
for the Magnetic Field Components m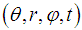 :
: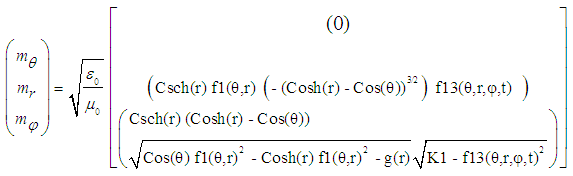 | (24) |
 direction. There is a resulting electromagnetic outward bounding force density in the r-direction,
direction. There is a resulting electromagnetic outward bounding force density in the r-direction, 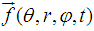 indicated as the outward bounding radiation pressure of the toroidal electromagnetic confinement.
indicated as the outward bounding radiation pressure of the toroidal electromagnetic confinement. 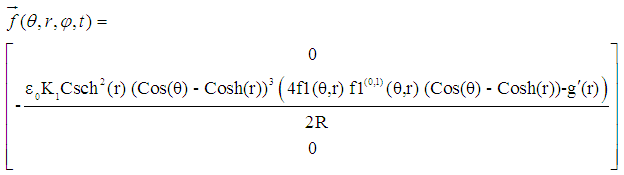 | (25) |
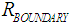 for the toroidal confinement can be calculated.
for the toroidal confinement can be calculated.7. Concluding Remarks
- The example of Gravitational-Electromagnetic Interaction, presented in table 1 shows two types of confinement. 1. For values
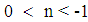 , the Gravitational-Electromagnetic Confinement will be Gravitationally controlled (Table 1). This means that for values for
, the Gravitational-Electromagnetic Confinement will be Gravitationally controlled (Table 1). This means that for values for 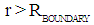 the inward bounded Gravitational for will be larger than the outward bounded Electromagnetic Radiation pressure. Electromagnetic Radiation will be attracted by Gravity towards the confinement at the surface
the inward bounded Gravitational for will be larger than the outward bounded Electromagnetic Radiation pressure. Electromagnetic Radiation will be attracted by Gravity towards the confinement at the surface 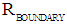 . Because for values
. Because for values 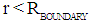 the outward bounded radiation pressure is higher than the inward bounded gravitational pressure, all the radiation will be forced to be confined at equilibrium just at the surface of the spherical sphere with radius
the outward bounded radiation pressure is higher than the inward bounded gravitational pressure, all the radiation will be forced to be confined at equilibrium just at the surface of the spherical sphere with radius 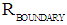 . The confinement can be considered as an Electromagnetic Black Hole. 2. For values
. The confinement can be considered as an Electromagnetic Black Hole. 2. For values 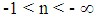 , the Gravitational-Electromagnetic Confinement will be Electromagnetically controlled (Table 1). This means that for values for
, the Gravitational-Electromagnetic Confinement will be Electromagnetically controlled (Table 1). This means that for values for 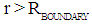 the inward bounded Gravitational for will be smaller than the outward bounded Electromagnetic Radiation pressure. Electromagnetic Radiation will be scattered by the Radiation Pressure away from the confinement at the surface
the inward bounded Gravitational for will be smaller than the outward bounded Electromagnetic Radiation pressure. Electromagnetic Radiation will be scattered by the Radiation Pressure away from the confinement at the surface 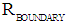 . Because for values
. Because for values 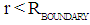 the outward bounded radiation pressure is smaller than the inward bounded gravitational pressure, all the radiation will be confined within the sphere with radius
the outward bounded radiation pressure is smaller than the inward bounded gravitational pressure, all the radiation will be confined within the sphere with radius 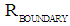 . The confinement can be considered as an Electromagnetic Particle. 3. For values
. The confinement can be considered as an Electromagnetic Particle. 3. For values 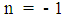 , the inward bounded Gravitational pressure equals the outward bounded Electromagnetic Radiation pressure at any distance r. The calculated value for
, the inward bounded Gravitational pressure equals the outward bounded Electromagnetic Radiation pressure at any distance r. The calculated value for 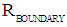 becomes
becomes 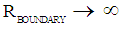 .Because of the extremely high-energy densities within electromagnetic-gravitational confinements and the extremely small dimensions, the radiation pressure at small densities will be extremely high. For this reason, electromagnetic-gravitational confinements will behave like nondeformable particles in experiments.
.Because of the extremely high-energy densities within electromagnetic-gravitational confinements and the extremely small dimensions, the radiation pressure at small densities will be extremely high. For this reason, electromagnetic-gravitational confinements will behave like nondeformable particles in experiments. ACKNOWLEDGMENTS
- This work has been made possible by the contributions of many. I am indebted to all and to my family, Lynn, Antonia and Julian in particular.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML