-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Astronomy
p-ISSN: 2169-8848 e-ISSN: 2169-8856
2015; 4(1): 1-4
doi:10.5923/j.astronomy.20150401.01
Kaluza-Klein Cosmological Model with Bulk Viscosity in Barber’s Second Self Creation Cosmology
R. Santhi Kumar1, D. R. K. Reddy2
1Department of Basic Science and Humanities, Aditya Institute of Technology and Management, Tekkali, Srikakulam, Andhra Pradesh, India
2Department of Science and Humanities, MVGR College of Engineering, Vizianagaram, Andhra Pradesh, India
Correspondence to: R. Santhi Kumar, Department of Basic Science and Humanities, Aditya Institute of Technology and Management, Tekkali, Srikakulam, Andhra Pradesh, India.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
A five dimensional Kaluza-Klein space-time is considered in the presence of a bulk viscous fluid in Barber’s (Gen.Relativ.Gravit.14:117, 1982) second self creation theory of gravitation. A barotropic equation of state for the pressure and density is assumed to get determinate solution of the field equations. Also, the bulk viscous pressure is assumed to be proportional to the energy density. Some physical and kinematical properties of the model are also discussed.
Keywords: Kaluze-Klein universe, Self creation cosmology, Bulk viscosity
Cite this paper: R. Santhi Kumar, D. R. K. Reddy, Kaluza-Klein Cosmological Model with Bulk Viscosity in Barber’s Second Self Creation Cosmology, International Journal of Astronomy, Vol. 4 No. 1, 2015, pp. 1-4. doi: 10.5923/j.astronomy.20150401.01.
Article Outline
1. Introduction
- It is well known that in recent years there has been a considerable interest in alternative theories of gravitation which are viable alternatives to general relativity. Brans and Dicke [2] formulated a scalar-tensor theory of gravitation which incorporates Machs-Principle in a relativistic frame work. Barber [1] proposed two continuous creation theories. The first is a modification of Brans - Dicke theory and the second is an adoption of general relativity to include continuous creation of matter and is within the limits of observation. These modified theories create the universe out of self contained gravitation and matter fields.Several authors have investigated various cosmological models in Barber’s second self creation theory [3-15] of some of the authors who have investigated several aspects of self creation theory.In recent years, cosmological models with bulk viscosity have gained importance, since viscosity appears as the only dissipative phenomenon occurring in Friedmann-Robertson- Walker (FRW) models and has a significant role in getting accelerated expansion of the universe popularly known as inflationary phase. Bulk viscosity contributes a negative pressure term giving rise to an effective total negative pressure stimulating repulsive gravity. The repulsive gravity overcomes the attractive gravity of matter and gives an impetus for rapid expansion of the universe. Bulk viscous cosmological models in general relativity have been discussed by several authors [16-33]. Bulk viscous cosmological models have been discussed in Brans-Dicke scalar-tensor theory of gravitation by some authors [34-36]. Very recently [37-46] have investigated Bianchi type cosmological models with cosmic strings and bulk viscosity in Saez - Ballester and Brans-Dicke scalar-tensor theories of gravitation. The study of higher dimensional space-time is important at early stages of evolution. Several [47-50] have studied higher dimensional cosmology because it has physical relevance to the early times before the universe has undergone compactification. Recently, several authors [32], [41-43] have obtained Kaluza – Klein models in modified theories of gravitation. Motivated by the above discussion and investigations we study, in this paper, Kaluza-Klein cosmological model in the presence of bulk viscosity in Barber’s second self creation theory. This model is a five dimensional cosmological model which will be useful to study the early stages of evolution in Barber’s second self creation theory. The plan of the paper is as follows: in Sec.2 explicit field equations are obtained in Barber’s second self creation theory with bulk viscous source with the aid of five dimensional Kaluza-Klein metric. Section 3 is devoted to the solution of highly non-linear field equations under same plausible conditions. The Kaluza-Klein bulk viscous model is presented in Barber’s second self creation theory. Some physical and Kinematical properties of the model are discussed in Sec.4. The last section contains conclusions.
2. Metric and Field Equations
- We consider a five dimensional Kaluza-Klein metric in the form
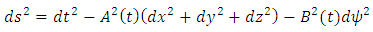 | (1) |
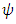 is taken to be space-like.The field equations in Barber’s [1] second self creation theory of gravitation are given by
is taken to be space-like.The field equations in Barber’s [1] second self creation theory of gravitation are given by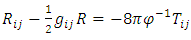 | (2) |
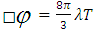 | (3) |
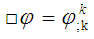 is the invariant d’Alembertian and T is the trace of the energy momentum tensor that describes all non-gravitational and non-scalar field theory. Barber’s scalar field φ is a function of t due to the nature of space-time which plays the role analogous to the reciprocal of Newtonian gravitational constant i.e.,
is the invariant d’Alembertian and T is the trace of the energy momentum tensor that describes all non-gravitational and non-scalar field theory. Barber’s scalar field φ is a function of t due to the nature of space-time which plays the role analogous to the reciprocal of Newtonian gravitational constant i.e., 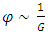 and coupling constant λ is determined from the experiment as
and coupling constant λ is determined from the experiment as 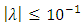 . In the limit as
. In the limit as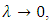 this theory approaches to the Einstein theory of gravity in every respect.We consider the energy momentum tensor for bulk viscous fluid as
this theory approaches to the Einstein theory of gravity in every respect.We consider the energy momentum tensor for bulk viscous fluid as 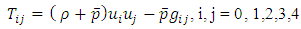 | (4) |
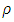 is the rest energy and
is the rest energy and 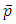 proper pressure together with
proper pressure together with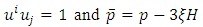 | (5) |
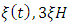 is usually known as a bulk viscous pressure, H is Hubble’s parameter,
is usually known as a bulk viscous pressure, H is Hubble’s parameter, 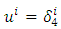 is a four velocity for i=0,1,2,3,4. We assume that the coordinate to be co-moving so that
is a four velocity for i=0,1,2,3,4. We assume that the coordinate to be co-moving so that 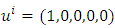 . Here after semi-colon (;) denotes covariant differentiation.Using, co-moving coordinates, the field equations (2)-(3) for the metric (1) with the help of (4)-(5) yield the following independent equations.
. Here after semi-colon (;) denotes covariant differentiation.Using, co-moving coordinates, the field equations (2)-(3) for the metric (1) with the help of (4)-(5) yield the following independent equations.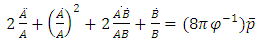 | (6) |
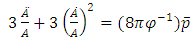 | (7) |
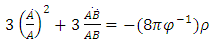 | (8) |
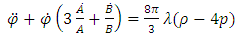 | (9) |
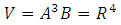 | (10) |
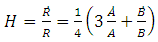 | (11) |
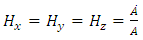 and
and 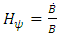 The scalar expression
The scalar expression 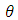 for the metric (2.1) is defined as
for the metric (2.1) is defined as 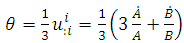 | (12) |
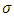 for the metric (1) is defined as
for the metric (1) is defined as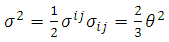 | (13) |
3. Solutions and the Model
- The field equations (6)-(9) are a system of four independent equations in five unknowns A, B,
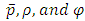 . Also the field equations are highly non-linear in nature and therefore we require the following plausible physical conditions:
. Also the field equations are highly non-linear in nature and therefore we require the following plausible physical conditions:3.1. The shear Scalar σ is Proportional to Scalar Expansion θ, so that We can Take
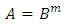 | (14) |
3.2. For a Barotropic Fluid, the Combined Effect of the Proper Pressure and the Barotropic Bulk Viscous Pressure can be Expressed as
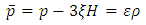 | (15) |
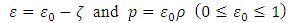
3.3. The Trace of the Energy Tensor is Zero i.e. T= 0 which Yields from Eq.(9) Reddy [44], Vidyasagar [45-46]
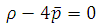 | (16) |
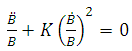 | (17) |
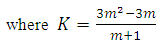 | (18) |
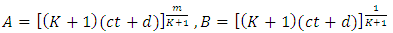 | (19) |
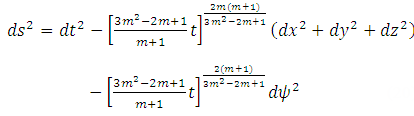 | (20) |
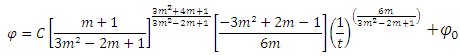 | (21) |
 are integration constants and C=1,
are integration constants and C=1,  without loss of generality, so that we have
without loss of generality, so that we have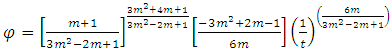 | (22) |
4. Physical and Kinematical Properties of the Model
- Eq.(20) represents a five dimensional Kaluza-Klein cosmological model with bulk viscosity in Barber’s second self creation theory.Spatial volume for the metric (1) is
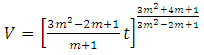 | (23) |
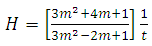 | (24) |
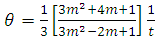 | (25) |
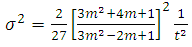 | (26) |
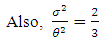 | (27) |
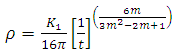 | (28) |
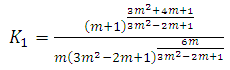 The proper pressure for the metric (1) is
The proper pressure for the metric (1) is 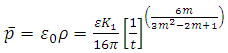 | (29) |
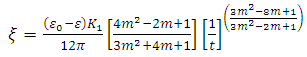 | (30) |
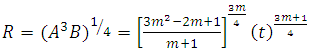 | (31) |
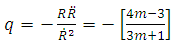 | (32) |
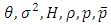 diverge for t=0 while they vanish for infinitely large t. However, the bulk viscosity becomes infinitely large as t→0, while it vanishes as t→∞ shown in fig 4. Also, since
diverge for t=0 while they vanish for infinitely large t. However, the bulk viscosity becomes infinitely large as t→0, while it vanishes as t→∞ shown in fig 4. Also, since 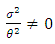 the model does not approach isotrophy (anisotropy model) throughout the evolution of the universe. The scalar field φ in the model diverge for t=0, while it vanishes as t→∞.
the model does not approach isotrophy (anisotropy model) throughout the evolution of the universe. The scalar field φ in the model diverge for t=0, while it vanishes as t→∞.5. Conclusions
- In this paper, we have investigated the field equations for a five dimensional Kaluza-Klein model in presence of bulk viscosity within the frame work of Barber’s second self creation theory. A barotropic cosmic fluid is considered for the study. A general equation of state for energy density is assumed. We have also assumed that the scalar expansion θ is proportional to the shear scalar σ to get determinate solution. The solution presented will help to discuss the role of bulk viscosity in getting an inflationary model in five dimensional Kaluza-Klein model in presence of bulk viscosity within the frame work of Barber’s second self creation theory.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML