-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Astronomy
p-ISSN: 2169-8848 e-ISSN: 2169-8856
2014; 3(2): 35-39
doi:10.5923/j.astronomy.20140302.02
The Structure of Solitary Dipole Vortises in Rotating Gaseous Gravitating Disc
M. G. Abrahamyan
Yerevan State University, Armenia
Correspondence to: M. G. Abrahamyan, Yerevan State University, Armenia.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
The structure of a solitary dipole vortex (modon) in rotating gaseous gravitating disc has been investigated. The velocity field of modon always has a dipolar structure. The two types of distribution of mass in a modon have been found. The first type is characterized by anti-symmetrically located one round condensation and one rarefaction. The second type is characterized by anti-symmetrically located two consolidations and two rarefactions, and the second pair condensation-rarefaction is crescent. The surfaces of constant-density of modon that are much smaller than the Jeans length λJ coincide with stream-lines; the constant-density surfaces of larger modons do not coincide with stream-lines. We discuss the possible astrophysical manifestations of modons in astrophysical objects.
Keywords: Vortex, Dipole, Structure, Gravitating disc
Cite this paper: M. G. Abrahamyan, The Structure of Solitary Dipole Vortises in Rotating Gaseous Gravitating Disc, International Journal of Astronomy, Vol. 3 No. 2, 2014, pp. 35-39. doi: 10.5923/j.astronomy.20140302.02.
Article Outline
1. Introduction
- The nonlinear fluid equations describing the dynamics of two-dimensional vortices are of great importance in oceanic and atmospheric physics, in plasma physics and in astrophysics. All these vortical structures are described by the same type of non-linear equations. In hydrodynamics this is known as the Hasegawa-Mima equation [1]
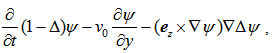 | (1) |
2. The Model and the Basic Equations
- Let there be a gravitating barotropic gaseous disc of density ρ0(r) rotating uniform with angular velocity Ω about the z-axis. We will examine isentropic two-dimensional in plane of disc perturbations, neglecting its vertical structure, and presenting any perturbed function f as
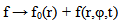 | (2) |
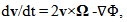 | (3) |
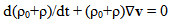 | (4) |
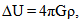 | (5) |
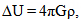 | (6) |
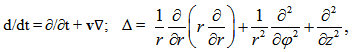 | (7) |
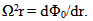 | (8) |
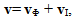 | (9) |
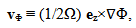 | (10) |
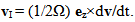 | (11a) |
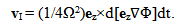 | (11b) |
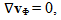 | (12) |
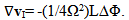 | (13) |
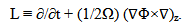 | (14) |
 | (15) |
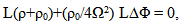 | (16) |
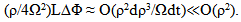 | (17) |
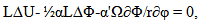 | (18) |
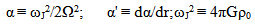 | (19) |
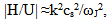 | (20) |
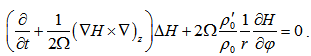 | (21) |
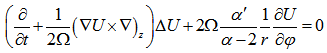 | (22) |
3. Modons and Their Velocity Field
- Let’s introduce local Cartesian coordinates (x,y) defined such that (Fig.1)
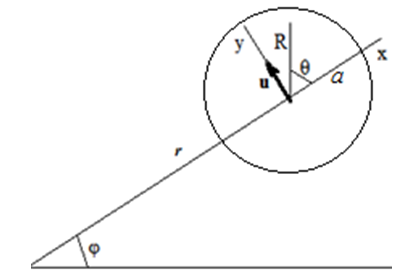 | Figure 1. |
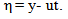 | (23) |
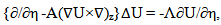 | (24) |
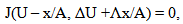 | (25) |
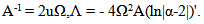 | (26) |
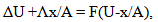 | (27) |
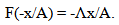 | (28) |
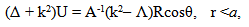 | (29) |
 | (30) |
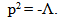 | (31) |
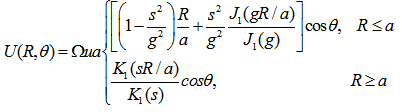 | (32) |
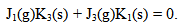 | (33) |
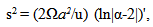 | (34) |
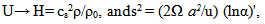 | (35) |
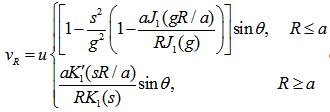 | (36) |
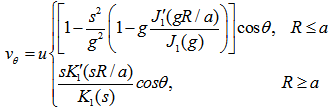 | (37) |
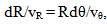 | (38) |
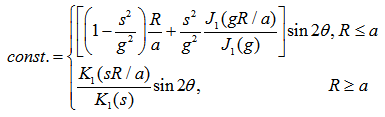 | (39) |
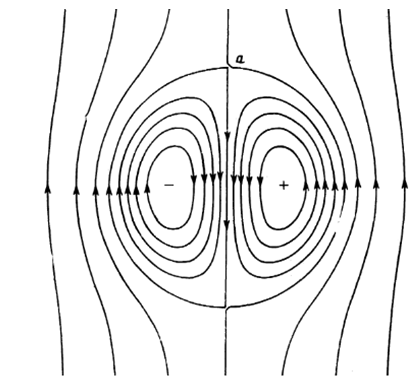 | Figure 2. The modon stream lines |
4. The Constant-Density Contours
- By the condition d/Ωdt≪ 1 we can omit the first term in equation (3), and obtain
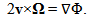 | (40) |
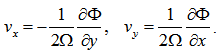 | (41) |
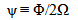 | (42) |
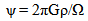 | (43) |
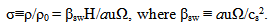 | (44) |
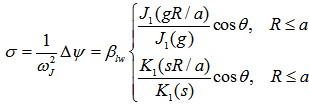 | (45) |
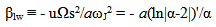 | (46) |
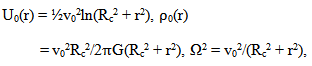 | (47) |
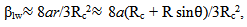 | (48) |
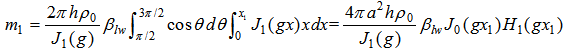 | (49) |
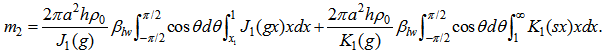 | (50) |
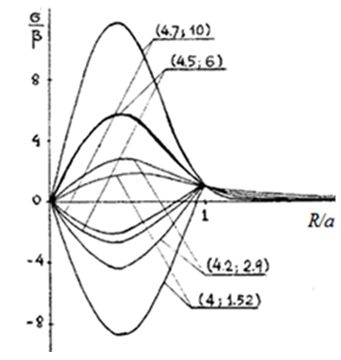 | Figure 3. |
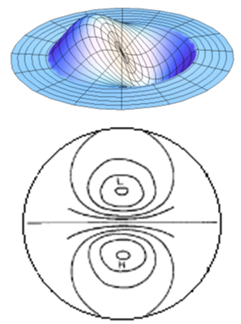 | Figure 4. |
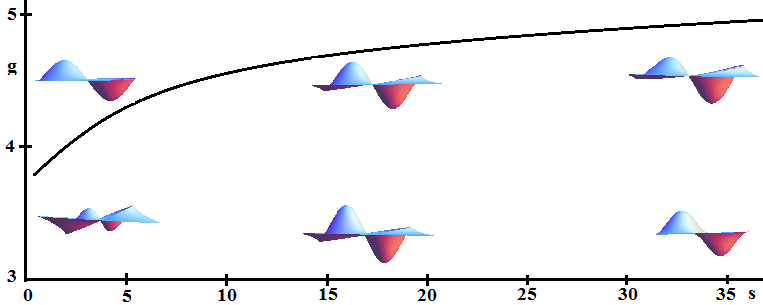 | Figure 4b. A dispersive curve (33) in the (s,g) plane. 3D density profile of long-wave (upper row) modons and short-wave modons. Blue color indicate condensation, red – rarefaction |
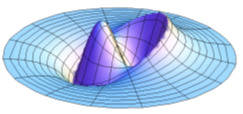 | Figure 5. The second type modon is characterized by two condensations and two rarefactions |
5. Conclusions
- So we would like to pay attention on the existence of double vortices in rotating gaseous gravitating discs and their nontrivial structure. It is difficult to say about a way of a modon evolution: if it could transform to well-known double objects such as double stars, double nuclei in galaxies (like Mrk 266 [19], see Fig.6) as well as in giant molecular clouds etc. or not. The importance of such origin of observed double objects would be the subject of discovery in forthcoming papers.
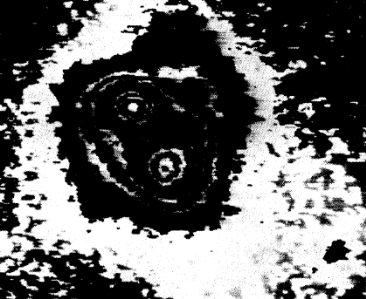 | Figure 6. The isodense picture of the galaxy Markaryan 266 with two nuclei, rotating in the opposite direction [19] |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML