-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Astronomy
p-ISSN: 2169-8848 e-ISSN: 2169-8856
2013; 2(3): 43-49
doi:10.5923/j.astronomy.20130203.04
Diagnostics of SGR Magnetospheres Using Coronal Seismology
A. V. Stepanov1, V. V. Zaitsev2
1Pulkovo Observatory, St.-Petersburg, 196140, Russia
2Institute of Applied Physics, Nizhny Novgorod, 603600, Russia
Correspondence to: A. V. Stepanov, Pulkovo Observatory, St.-Petersburg, 196140, Russia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
We develop a method of diagnostics of magnetospheres of soft gamma-ray repeaters (SGRs) using high-frequency (20-2400 Hz) quasi-periodic pulsations (QPOs)[14]. The trapped fireball is represented as a set of current-carrying loops, equivalent RLC-circuits, rooted into a neutron star surface. The model explains the observed periods of QPOs and their high quality factor Q ≈ 104-105. The parameters of the source of the pulsations at the «ringing tail» stage for three well-known giant SGR flares are determined: the electric current I≈ (2-8)×1019 A, the magnetic field B ≈ (0.6-2.7)×1013 G < BQ, and the electron number density n ≈ (1.3-6.0)×1016 cm-3. We also show that high-frequency QPOs can be self-excited for an electric current smaller than the maximum current in the giant pulse of the flare, and/or due to the parametric resonance. The result is consistent with the conclusion made by Rea et al.[11] that a high surface magnetic field is not necessarily required for the magnetar activity.
Keywords: Magnetars, Quasi-Periodic Oscillations, Coronal Loops, Magnetic Field
Cite this paper: A. V. Stepanov, V. V. Zaitsev, Diagnostics of SGR Magnetospheres Using Coronal Seismology, International Journal of Astronomy, Vol. 2 No. 3, 2013, pp. 43-49. doi: 10.5923/j.astronomy.20130203.04.
Article Outline
1. Introduction
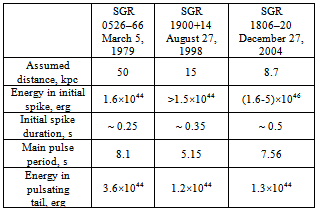
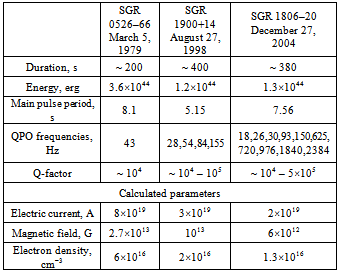
- The strongest cosmic magnets, magnetars, are historically divided into two classes of neutron stars: soft gamma-ray repeaters (SGRs) detected in the hard X-ray/soft-gamma ray band, and anomalous X-ray pulsars (AXPs) first detected in soft X-rays (< 10 keV). Their activity is powered by the decay of ultrastrong magnetic fields and lasts about 103-105 years (see, e.g., a review[1]). The current information on 23 magnetars is held in McGill SGR/AXP Online Catalog[2]. In the last decade, the primary consideration has been received by SGRs related to very high energy release in the flares, up to 5×1046 erg. The peak luminosity of SGR giant flares Lx ≈2×1044-5×1047erg s-1 substantially exceeds any previous transient event observed in our Galaxy. The radiation flux from giant SGR flares is so huge that it is reflected by the ionisation level in the bulk of the Earth’s ionosphere by several orders of magnitude and the SGR rotating period modulates the ionisation despite the fact that the source is several tenths thousands light years away. For example, the giant SGR 1806-20 flare on December 27th 2004 created disturbances in the daytime lower ionosphere corresponding to the increase in electron density by 2-3 orders of magnitude[3]. Moreover, the lunar echo from SGR 1806-20 flare clearly affected the night dark polar ionosphere[4].Currently, it is suggested that SGRs are isolated rotating neutron stars with the radius ~ 10 km, the mass ~ 1.5 MSun, and the spin period 2 to 10 s. SGRs have external magnetic fields of the order of 1014-1015 G, two-to-three orders higher than those in classical radio pulsars, and internal fields that can reach 1016 G[5]. Three giant flares of magnetars (Table 1), which occurred on 1979 March 5th (SGR 0526-66), on 1998 August 27th (SGR 1900+14), and on 2004 December 27th (SGR 1806-20), with an energy release of (2-500)×1044 erg, were accompanied by the “ringing tails” ofhigh-frequency (tens to thousands Hz) quasi-periodic oscillations (QPOs) of the X-ray emission[6],[7],[8].
|
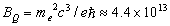 G at which the nonrelativistic Landau energy
G at which the nonrelativistic Landau energy 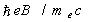 becomes equal to the electron rest energy
becomes equal to the electron rest energy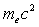 . However, there are evidences for the existence of SGRs with low magnetic fields. Rea et al.[11] described SGR 0418+5729 with the dipolar magnetic field B < 7.5×1012 G. X-ray observations of the outburst of the magnetar J1822.3-1606 made with Swift, Rossi X-Ray Timing Explorer (RXTE), Chandra, and X-ray Multi-Mirror Mission-Newton (XMM-Newton) yielded the surface magnetic field B ≈ 2.7×1013 G < BQ[12]. Moreover, Malov[13] concluded that even a magnetic field of 1016 G in the stellar interior cannot explain the giant outbursts of SGRs and that the existence of low-magnetic-field SGRs indicates that the main attribute of a magnetar (B > BQ) may not be inherent in all SGRs/AXPs.To estimate the surface magnetic field strength, several methods are used, based on various physical phenomena: the spin-down rate, the ion cyclotron resonance, peculiarities of QPOs. Recently, we proposed an independent diagnostic method based on coronal seismology, using the parameters of trapped fireball plasma[14]. The Alfvén and Carlqist’s[15] concept of a flare loop as an equivalent electric circuit is the basement of this method. Our approach considers a trapped fireball, the source of high-frequency QPOs, as a set of current-carrying loops, which can be represented as equivalent RLC-circuits. Using the period and the Q-factor of QPOs we can estimate the electric current, magnetic field, and electron density in QPO sources.This paper is devoted to the further applications of our diagnostic method of SGR coronae based on coronal seismology. Section 2 presents a brief description of the existing methods of the evaluation of magnetic fields. Exsisting QPO models are discussed in Section 3. In Section 4 we use QPO characteristics to diagnose physical parameters of magnetospheres for three well-known giant SGR flares. Excitation mechanisms of QPOs will be analyzed in Section 5. Section 6 presents discussion and conclusions.
. However, there are evidences for the existence of SGRs with low magnetic fields. Rea et al.[11] described SGR 0418+5729 with the dipolar magnetic field B < 7.5×1012 G. X-ray observations of the outburst of the magnetar J1822.3-1606 made with Swift, Rossi X-Ray Timing Explorer (RXTE), Chandra, and X-ray Multi-Mirror Mission-Newton (XMM-Newton) yielded the surface magnetic field B ≈ 2.7×1013 G < BQ[12]. Moreover, Malov[13] concluded that even a magnetic field of 1016 G in the stellar interior cannot explain the giant outbursts of SGRs and that the existence of low-magnetic-field SGRs indicates that the main attribute of a magnetar (B > BQ) may not be inherent in all SGRs/AXPs.To estimate the surface magnetic field strength, several methods are used, based on various physical phenomena: the spin-down rate, the ion cyclotron resonance, peculiarities of QPOs. Recently, we proposed an independent diagnostic method based on coronal seismology, using the parameters of trapped fireball plasma[14]. The Alfvén and Carlqist’s[15] concept of a flare loop as an equivalent electric circuit is the basement of this method. Our approach considers a trapped fireball, the source of high-frequency QPOs, as a set of current-carrying loops, which can be represented as equivalent RLC-circuits. Using the period and the Q-factor of QPOs we can estimate the electric current, magnetic field, and electron density in QPO sources.This paper is devoted to the further applications of our diagnostic method of SGR coronae based on coronal seismology. Section 2 presents a brief description of the existing methods of the evaluation of magnetic fields. Exsisting QPO models are discussed in Section 3. In Section 4 we use QPO characteristics to diagnose physical parameters of magnetospheres for three well-known giant SGR flares. Excitation mechanisms of QPOs will be analyzed in Section 5. Section 6 presents discussion and conclusions.2. Magnetic Field Diagnostic Methods
- The most popular method of estimation of the surface dipolar field is the rate of kinetic energy loss via magnetic-dipole radiation:
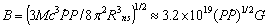 | (1) |
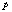 is the spin down rate; it is assumed that Rns ≈ 106 cm and M ≈ 1045 g cm2 for the star radius and momentum of inertia. Most of the sources with magnetar-like activity have rotational periods 2--12 s and period derivatives 10-13 – 10-10 ss-1. Therefore, the dipolar field spans 5×1013 - 2×1014 G[1]. These values exceed the average field in radio pulsars by one to three orders of magnitude; they also exceed the electron quantum field
is the spin down rate; it is assumed that Rns ≈ 106 cm and M ≈ 1045 g cm2 for the star radius and momentum of inertia. Most of the sources with magnetar-like activity have rotational periods 2--12 s and period derivatives 10-13 – 10-10 ss-1. Therefore, the dipolar field spans 5×1013 - 2×1014 G[1]. These values exceed the average field in radio pulsars by one to three orders of magnitude; they also exceed the electron quantum field 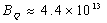 G. Besides, magnetars have a relatively small age
G. Besides, magnetars have a relatively small age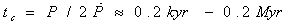 . High surface field strength ~ 1015 G cannot result in a powerful energy release ~ 5×1046 erg; it could only be possible either if the mechanism of the flare was extremely efficient or if the interior field was substantially stronger and reached 1016 G[16]. Recent observations of SGR 0418+5729 yield P ≈ 9.1 s, the upper limit
. High surface field strength ~ 1015 G cannot result in a powerful energy release ~ 5×1046 erg; it could only be possible either if the mechanism of the flare was extremely efficient or if the interior field was substantially stronger and reached 1016 G[16]. Recent observations of SGR 0418+5729 yield P ≈ 9.1 s, the upper limit 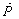 < 6×10-15 ss-1, and the corresponding limit on the surface magnetic field B < 7.5×1012 G[11]. The upper limit for
< 6×10-15 ss-1, and the corresponding limit on the surface magnetic field B < 7.5×1012 G[11]. The upper limit for 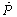 implies a characteristic age tc > 24 Myr. With these parameters, the internal toroidal field for SGR 0418+5729 can be estimated as
implies a characteristic age tc > 24 Myr. With these parameters, the internal toroidal field for SGR 0418+5729 can be estimated as 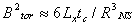 [5]. Assuming the source distance of 2 Kpc and Lx ≈ 6.2×1031 erg s-1, one can obtain Btor ≈ 5×1014 G. SGR 0418+5729 may represent the population of low-dipolar-field magnetars that are dissipating the last bit of their internal energy[11]. Another example for a low-magnetic-field magnetar is presented by SGR 1822-1606, with P ≈ 8.44 s,
[5]. Assuming the source distance of 2 Kpc and Lx ≈ 6.2×1031 erg s-1, one can obtain Btor ≈ 5×1014 G. SGR 0418+5729 may represent the population of low-dipolar-field magnetars that are dissipating the last bit of their internal energy[11]. Another example for a low-magnetic-field magnetar is presented by SGR 1822-1606, with P ≈ 8.44 s, 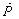 ≈ 8.3×10-14 ss-1, which yields B ≈ 2.7×1013 G < BQ and tc ≈ 1.6 Myr[12].Some models of X-ray spectra suggest a strong absorption line of the proton cyclotron resonance; hence B ≈ 1.6(1+z)Ec(keV)×1014G, where z ≈ 0.3 is the gravitational redshift. For Ec = 5 keV, absorption features in SGR 1806-20 bursts give B ≈ 1015 G[17]. On the other hand, the evidence for the emission line at 6.4 keV obtained during the bursts of SGR 1990+14 with Rossi X-Ray Timing Explorer (RXTE) implies the surface field strength B ≈ (1.3-2.6)×1015 G, depending on the proton or He4 cyclotron resonance[18]. An independent evidence for the superstrong surface magnetic field in SGR 1806-20 was obtained by Vietri et al.[19]. They pointed out the largest luminosity variation
≈ 8.3×10-14 ss-1, which yields B ≈ 2.7×1013 G < BQ and tc ≈ 1.6 Myr[12].Some models of X-ray spectra suggest a strong absorption line of the proton cyclotron resonance; hence B ≈ 1.6(1+z)Ec(keV)×1014G, where z ≈ 0.3 is the gravitational redshift. For Ec = 5 keV, absorption features in SGR 1806-20 bursts give B ≈ 1015 G[17]. On the other hand, the evidence for the emission line at 6.4 keV obtained during the bursts of SGR 1990+14 with Rossi X-Ray Timing Explorer (RXTE) implies the surface field strength B ≈ (1.3-2.6)×1015 G, depending on the proton or He4 cyclotron resonance[18]. An independent evidence for the superstrong surface magnetic field in SGR 1806-20 was obtained by Vietri et al.[19]. They pointed out the largest luminosity variation 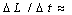 6×1043 erg s-2 in the fastest (625 and 1840 Hz) QPOs in the ringing tail of the 2004 December 27 event in SGR 1806-20, which exceeded the common Cavallo-Fabian-Rees luminosity variability limit
6×1043 erg s-2 in the fastest (625 and 1840 Hz) QPOs in the ringing tail of the 2004 December 27 event in SGR 1806-20, which exceeded the common Cavallo-Fabian-Rees luminosity variability limit 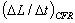 < 2×1042 erg s-2 (for a matter-to-radiation conversion efficiency of 100%) by more than an order of magnitude. According to[19], such high
< 2×1042 erg s-2 (for a matter-to-radiation conversion efficiency of 100%) by more than an order of magnitude. According to[19], such high 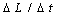 may be due to the vacuum polarization effect, which reduces the scattering cross-section with respect to the Thompson’s because of the presence of a strong magnetic field B ≥ 6.6×1013 G in the 30 km size QPO source. Hence the magnetic field on the star surface is B ≥ 1015 G[19].
may be due to the vacuum polarization effect, which reduces the scattering cross-section with respect to the Thompson’s because of the presence of a strong magnetic field B ≥ 6.6×1013 G in the 30 km size QPO source. Hence the magnetic field on the star surface is B ≥ 1015 G[19]. 3. Existing Models of QPOs
- Three giant flares of SGRs were accompanied by high-frequency (tens to thousands Hz) quasi-periodic X-ray pulsations (Table 2). Such pulsations were observed not only in flare tails, 100 to 300 s after the main pulse, which lasted ≤ 1 s, but also at the growth phase of the main pulse[6],[16]. The greatest variety of the pulsations, from 18 to 2384 Hz (Figure 1), were detected by RXTE and Reuven Ramaty High Energy Solar Spectroscopic Imager (RHESSI) space missions in the «ringing tail» of the flare of SGR 1806-20[20].
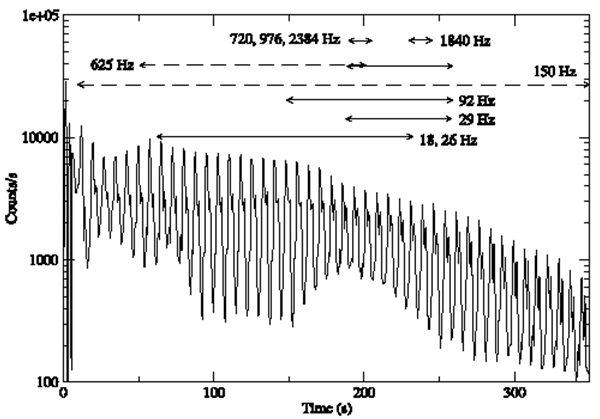 | Figure 1. Time periods for various fast QPOs (18 to 2384 Hz) detectable by RXTE and RHESSI in the ‘ringing tail’ of SGR 1806-20. The spin period is 7.56 s[20] |
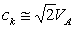 derived in[25] has no physical meaning. Moreover, instead of the general formula for the Alfvén velocity (5), the expression
derived in[25] has no physical meaning. Moreover, instead of the general formula for the Alfvén velocity (5), the expression 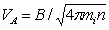 was used in[25]. This resulted in VA >> c even for B ≈ 1014 G, and the plasma number density n ≈ 1028 cm-3.
was used in[25]. This resulted in VA >> c even for B ≈ 1014 G, and the plasma number density n ≈ 1028 cm-3.4. The Suggested Approach: An Equivalent Electric (RLC) Circuit
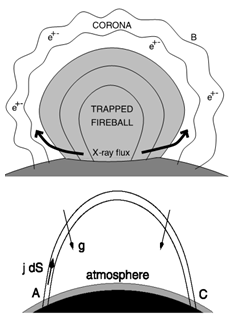
- Our model for high-frequency pulsations in magnetars is based on the ideas of coronal seismology, which studies oscillations and waves in stellar coronae[26]. Coronal seismology appeared to be very efficient in diagnostics of the parameters of the coronae and flare plasma not only in the Sun, but also in late-type stars[27]. Currently, two approaches are developed in coronal seismology. The first one studies MHD-oscillations and waves in the basic structures of stellar coronae – coronal magnetic loops. In these formations, flare energy release occurs. The other approach is based on the Alfvén and Carlqvist’s[15] idea, according to which a flare loop is considered as an equivalent electric circuit. The basic concepts of this approach are presented in the review of Khodachenko et al.[28] and in the book[26]. The corona of a magnetar and the trapped fireball, to which the ringing tail is generally related, may be presented as a set of current-carrying magnetic loops of various sizes (Figure 2), whose eigen-frequencies and quality factors are given by well-known expressions
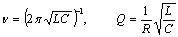 | (2) |
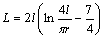 | (3) |
4.1. The Flare of SGR 1806-20 on December 27th 2004
- The ringing tail of the SGR 1806-20 giant flare on December 27th 2004 reveals the largest number of pulsation frequencies in the interval from 18 to 2384 Hz. The total energy released in this flare was of the order of 5×1046 erg, while the stored magnetic energy ~ 1047 erg[16]. The energy of the pulsating tail was of the order of 1044 erg[19]. Taking into account the great variety of QPO frequencies (Table 2), we will suggest that the energy stored in an ‘average’ loop in the course of the ‘ringing tail’ is roughly 1043 erg. Supposing the length and radius of a loop l = 3×106 cm and r = 3×105 cm, respectively, we can use Eqs. (3) to find its inductance L ≈ 5×106 cm = 5×10–3 Henry. Assuming that the stored energy of an ’average’ loop, E ≈ 1043 ergs = 1036 J, has been released, we obtain the current I = (2E/L)1/2 ≈ 2×1019 A, and from Biot-Savart law we estimate the φ-component of the magnetic field in the loop Bφ ≈ I/cr ≈ 6×1012 G. The density of electron-positron pairs n in the source of the tail will be obtained from the electric current I = encS and the cross section of the coronal loop S with the radius r = 3×105 cm. For I = 2×1019 A, n = 1.3×1016 cm-3, i.e., the Langmuir frequency νp = ωp/2π ≈ 1 THz corresponds to sub-millimeter wavelengths.The power of the energy release in the tail of a flare with the duration ≈ 200 s is of the order of ≈ 1041 erg/s[19] i.e. for an «average» loop, the power is W=RI2 ≈ 1040 erg/s = 1033 W. The resistance of a loop in the ringing tail of the flare of SGR 1806-20 is R = W/I2 ≈ 2×10-6 Ω. This resistance value may be due to anomalous conductivity that emerges in the course of excitation of small-scale plasma waves. The effective (turbulent) resistance may be presented in the form
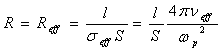 | (4) |
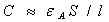 , where
, where 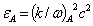 is the dielectric permittivity for Alfvén waves. If the displacement current is included in the analysis, the dispersion relation for Alfvén waves is[29]
is the dielectric permittivity for Alfvén waves. If the displacement current is included in the analysis, the dispersion relation for Alfvén waves is[29] 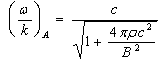 | (5) |
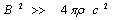 the Alfvén velocity is roughly equal to c. Therefore, εA ≈ 1, and for the assumed cross-section of the loop S = πr2 ≈ 3×1011 cm2 and its length l = 3×106 cm, we obtain C ≈ 105 cm =10-7 F, which is by the factor of a few lower than that (C2) calculated from the formula (2). Note that the sizes of coronal loops in the trapped fireball may differ by several orders of magnitude. We can see that with an increase in the cross-section S and a decrease in the loop length l (a «thick» loop), the coincidence between the calculated capacity C and both C2 and C1 may be reached. Using the second relation from the formula (2), we can find the quality factors for the minimum and maximum frequency: Q1 ≈ 3×105 and Q2 ≈ 107, which exceed the observed quality factors of the QPO by one or two orders of magnitude. This discrepancy may be due to both an insufficient sensitivity of the detectors, and the «cooling» of the trapped fireball. Our model suggests that oscillations of electric current should be in-phase in all points of a loop. On the other hand, variations of the current propagate along the loop with the Alfvén velocity. Therefore, for the condition of phase coincidence, the Alfvén time should be substantially smaller than the period of oscillations. For SGRs considered here, the in-phase condition is satisfied, νRLC ≈ 20-2500 Hz < νA ≈ c/l ≥ 104 Hz, because in magnetar coronae VA ≈ c. The same method was applied to the determination of magnetosphere parameters of the giant flares in SGR 0526–66 (March 5th 1979) and SGR 1900+14 (August 27th 1998). Table 2 presents the data of observations of “ringing tails” with QPOs and the results of calculations of magnetosphere parameters. One can see that our diagnostic method yields the magnetic field in the SGR magnetospheres, which does not exceed the Schwinger critical value B ≈ (6-27)×1012 G < BQ.
the Alfvén velocity is roughly equal to c. Therefore, εA ≈ 1, and for the assumed cross-section of the loop S = πr2 ≈ 3×1011 cm2 and its length l = 3×106 cm, we obtain C ≈ 105 cm =10-7 F, which is by the factor of a few lower than that (C2) calculated from the formula (2). Note that the sizes of coronal loops in the trapped fireball may differ by several orders of magnitude. We can see that with an increase in the cross-section S and a decrease in the loop length l (a «thick» loop), the coincidence between the calculated capacity C and both C2 and C1 may be reached. Using the second relation from the formula (2), we can find the quality factors for the minimum and maximum frequency: Q1 ≈ 3×105 and Q2 ≈ 107, which exceed the observed quality factors of the QPO by one or two orders of magnitude. This discrepancy may be due to both an insufficient sensitivity of the detectors, and the «cooling» of the trapped fireball. Our model suggests that oscillations of electric current should be in-phase in all points of a loop. On the other hand, variations of the current propagate along the loop with the Alfvén velocity. Therefore, for the condition of phase coincidence, the Alfvén time should be substantially smaller than the period of oscillations. For SGRs considered here, the in-phase condition is satisfied, νRLC ≈ 20-2500 Hz < νA ≈ c/l ≥ 104 Hz, because in magnetar coronae VA ≈ c. The same method was applied to the determination of magnetosphere parameters of the giant flares in SGR 0526–66 (March 5th 1979) and SGR 1900+14 (August 27th 1998). Table 2 presents the data of observations of “ringing tails” with QPOs and the results of calculations of magnetosphere parameters. One can see that our diagnostic method yields the magnetic field in the SGR magnetospheres, which does not exceed the Schwinger critical value B ≈ (6-27)×1012 G < BQ.
|
5. Excitation of High-frequency Oscillations of the Current in Coronal Loops
- For minor deviations of the electric current
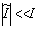 , the equation that describes oscillations of the electric current in a loop may be presented in the form[28]:
, the equation that describes oscillations of the electric current in a loop may be presented in the form[28]: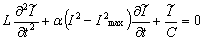 | (6) |
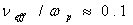 . This value was used before to obtain the level of small-scale turbulence in a QPO source which determines the effective resistance of “average” loop. Equation (6) indicates that oscillations will be excited for a current smaller than the maximum current in the giant pulse of the flare, I < Imax, that is, not only at the descending, but also at the ascending stage of the flare. Recall that pulsations with the frequency 43 Hz in SGR 0526-66[6] and 50 Hz in SGR 1806-20[16] were also observed at the ascending stage of the pulse phase.Consider another possible way of generation of oscillations in coronal magnetic loops – excitation due to parametric resonance[30]. As a result of parametric interaction with the coronal loop, the oscillations of the electric current due to perturbations in the crust of the magnetar with the pumping frequency ν may trigger ocsillations in the loop, with the frequency ν, at the sub-harmonics ν/2, and at the first upper frequency of the parametric resonance 3ν/2. A similar effect is observed in the optical and microwave radiation of solar flares[30]. Variations of the parameters of a coronal loop may be described with the equation
. This value was used before to obtain the level of small-scale turbulence in a QPO source which determines the effective resistance of “average” loop. Equation (6) indicates that oscillations will be excited for a current smaller than the maximum current in the giant pulse of the flare, I < Imax, that is, not only at the descending, but also at the ascending stage of the flare. Recall that pulsations with the frequency 43 Hz in SGR 0526-66[6] and 50 Hz in SGR 1806-20[16] were also observed at the ascending stage of the pulse phase.Consider another possible way of generation of oscillations in coronal magnetic loops – excitation due to parametric resonance[30]. As a result of parametric interaction with the coronal loop, the oscillations of the electric current due to perturbations in the crust of the magnetar with the pumping frequency ν may trigger ocsillations in the loop, with the frequency ν, at the sub-harmonics ν/2, and at the first upper frequency of the parametric resonance 3ν/2. A similar effect is observed in the optical and microwave radiation of solar flares[30]. Variations of the parameters of a coronal loop may be described with the equation 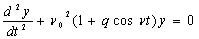 | (7) |
6. Discussion and Conclusions
- QPO models based both on global seismic ocsillations and on MHD-oscillations in coronal magnetic loops face difficulties in explanation for both the observed periods of oscillations and their high quality factors. Firstly, seismic oscillations do not explain pulsations with the frequencies 18 and 26 Hz[8]. Secondly, there are problems with MHD-oscillation model for QPOs, mentioned in Section 3[25]. In addition to that, the existing models do not explain the excitation of the oscillations at the positive slope of the main pulse. Our model provides the explanation from a single point of fiew, and for the total set of the observed frequencies of pulsations, 20 to 2400 Hz, for the excitation of the oscillation both in the «tail» of the flare and at the beginning of the main pulse, and, which is particularly important, for the high quality factor of the pulsations Q ≥ 104. High-frequency variations of the current in coronal loops result in periodic variations of the magnetic field, which modulates the radiation of the magnetar. Although the suggested approach -- the description of coronal loops of a magnetar as equivalent RLC-circuits -- is largely phenomenological, it nonetheless makes it possible to estimate the parameters of the magnetosphere of a neutron star in an independent way.Currently, numerous techniques for the determination of the magnetic field of magnetars exist. From the deceleration of the rotation of magnetars, the field B ≈ 1014 - 1015 G is derived. From the proton cyclotron resonance, the value B ≈ 1015 G is obtained. From the model of QPO as Alfvén torsion oscillations, the magnetic field of SGR 1806-20 within the interval (3-7)×1015 G was found[32]. From the study of variations of the luminosity of pulsations with frequencies 625 and 1840 Hz in the ringing tail of SGR 1806-20, it was found that in the QPO source (a magnetar’s corona) the magnetic field B ≈ 6.6×1013 G, while on the surface of the star the dipole approximation yields B ≈ 2×1015 G. Our estimation for the values of the magnetic field in the QPO sources in SGR flares based on the electric current I = (2E/L)1/2 ≈ (2-8)×1019 A gives B ≈ (6-27)×1012 G < BQ. These values are consistent with the recent observations of low-magnetic field SGRs[11],[12], and with the idea that a high surface magnetic field is not necessary for the magnetar-like activity[11],[13]. It also means that the physical processes in magnetar magnetospheres at the “ringing tail” phase can be studied within the non-quantum electrodynamics approach. Within the RLC-model, the current values make it possible to estimate also the electron number density in SGR magnetospheres n ≈ (1.3-6)×1016 cm-3. We have to stress, however, that our estimates of the electric current and φ-component of the magnetic field in the ringing tail are based on the energy relation E = LI2/2. The energy of the ringing tail of the flare ~ 1044 erg is by more than two orders of magnitude less than the total flare energy. Hence, to answer the question about the origin of the magnetar-like activity of neutron stars, more multi-wavelength observations are required.
ACKNOWLEDGEMENTS
- This work was supported partially by RFBR grants 11-02-00103-a and 12-02-00616-a, the Programme for Leading Science Schools NSH 3645.2010.2 and 1625.2012.2, the Programme of the Presidium of RAS “The Origin and Evolution of Stars and Galaxies”, and under the Agreement with Ministry of Education and Science of Russia No 8714.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML