-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Arts
p-ISSN: 2168-4995 e-ISSN: 2168-5002
2012; 2(2): 1-7
doi:10.5923/j.arts.20120202.01
Golden Section Heat Engines and Heat Pumps
Mahmoud Huleihil1, 2, Gedalya Mazor2
12The Sami Shamoon College of Engineering, Israel
2The Sami Shamoon College of Engineering, Israel
Correspondence to: Mahmoud Huleihil, 2The Sami Shamoon College of Engineering, Israel.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this study the efficiency of heat engines and the coefficient of performance of heat pumps are reconsidered following the idea of the golden section ratio. Two models are analyzed: the golden section Carnot cycle and the golden section endo-reversible cycle. The observed expressions for efficiency and coefficient of performance are cast in terms of the golden section ratio. Single (steam turbines[40Wilfried, U., OMMI, vol. 2, issue 3, pp. 1-9, 2003]) and double (combined cycles[Ishikawa, M., Terauchi, M., Komori, T., Yasuraoka, J., Mitsubishi Heavy Industries, Ltd., Technical Review Vol. 45 No. 1, pp. 15-17, 2008]) heat engine cycles are considered. Expressions for the working fluid temperatures at the hot and cold sides are derived. Calculations performed on steam parameters, with the supercritical temperature of 610oC, show that the relative differences of the golden section single heat engine, when compared to the endo-reversible results, fell within the 2- 4% range, with relative power reductions of 15% from the maximum power point. Finally, it was shown that system efficiency differs by approximately 3.6% from the efficiency derived based on the golden section.
Keywords: Golden Section, Arts, Heat Engines, Heat Pump
Cite this paper: Mahmoud Huleihil, Gedalya Mazor, Golden Section Heat Engines and Heat Pumps, International Journal of Arts, Vol. 2 No. 2, 2012, pp. 1-7. doi: 10.5923/j.arts.20120202.01.
Article Outline
1. Introduction
- The Carnot engine constitutes the basic heat engine model. It has reversible processes and yields an upper bound of thermal efficiency for heat engines working between two heat reservoirs at constant temperatures. Practically, a Carnot engine yields zero power. When the power output is limited by the heat transfer rates between the heat reservoirs and the working substance, the heat engine is defined as endo-reversible. Using the endo-reversible cyclic model, Novikov[1] and Curzon and Ahlborn[2] have obtained
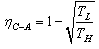 as the efficiency of a Carnot engine at maximum power output, in which
as the efficiency of a Carnot engine at maximum power output, in which 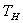 and
and 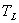 are temperatures of the heat source and sink, respectively. Following these studies, the methods of finite time thermodynamics (FTT) have been applied to a wide range of thermodynamic systems 3-27]. In a different approach, Popcov and Shipitsyn considered the golden section in the Carnot cycle 28]. In their study, some aspects of classical thermodynamics are analyzed for the presence of duality and of the golden section.In his book review 35], Markowsky gave some properties of the golden section. The number (1 +√5)/2 = 1.618… is widely known as the golden ratio,
are temperatures of the heat source and sink, respectively. Following these studies, the methods of finite time thermodynamics (FTT) have been applied to a wide range of thermodynamic systems 3-27]. In a different approach, Popcov and Shipitsyn considered the golden section in the Carnot cycle 28]. In their study, some aspects of classical thermodynamics are analyzed for the presence of duality and of the golden section.In his book review 35], Markowsky gave some properties of the golden section. The number (1 +√5)/2 = 1.618… is widely known as the golden ratio, 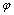 , and phi. Phi appears in many different equations and formulas and has many interesting properties. Markowsky claims that many people have heard marvelous tales about phi and how it permeates art and nature. Hretcanu and Crasmareanu[9] claim that the golden ratio (also known as the golden section) is a fascinating topic that continually generates new ideas. The main purpose of their paper was to point out and find some applications of the golden ratio and of Fibonacci numbers in differential geometry. They studied a structure defined on a class of Riemannian manifolds, called by them a golden structure. A Riemannian manifold endowed with a golden structure was called a golden Riemannian manifold.Watson[30] states that the golden section is intimately related to growth and nature. Moreover, he claims that eggs, an apple blossom, a human face, a seashell—all embody golden section proportions. He believes that the golden section is a simple tool that may be used to enhance the meaning and beauty of an architectural work. Based on that, he says that designing buildings with this knowledge automatically creates harmonizing, uplifting effects on those who experience them. Watson also claims that when the structural lines of a building are designed according to the principles of harmonic proportions, a natural aesthetic beauty results—beauty that can benefit those who work, live, and play within those environments. On the other hand, Kak[31], reported in his article that the golden mean,
, and phi. Phi appears in many different equations and formulas and has many interesting properties. Markowsky claims that many people have heard marvelous tales about phi and how it permeates art and nature. Hretcanu and Crasmareanu[9] claim that the golden ratio (also known as the golden section) is a fascinating topic that continually generates new ideas. The main purpose of their paper was to point out and find some applications of the golden ratio and of Fibonacci numbers in differential geometry. They studied a structure defined on a class of Riemannian manifolds, called by them a golden structure. A Riemannian manifold endowed with a golden structure was called a golden Riemannian manifold.Watson[30] states that the golden section is intimately related to growth and nature. Moreover, he claims that eggs, an apple blossom, a human face, a seashell—all embody golden section proportions. He believes that the golden section is a simple tool that may be used to enhance the meaning and beauty of an architectural work. Based on that, he says that designing buildings with this knowledge automatically creates harmonizing, uplifting effects on those who experience them. Watson also claims that when the structural lines of a building are designed according to the principles of harmonic proportions, a natural aesthetic beauty results—beauty that can benefit those who work, live, and play within those environments. On the other hand, Kak[31], reported in his article that the golden mean, 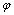 , has been applied in diverse situations in art, architecture, and music, and although some have claimed that it represents a basic aesthetic proportion, others have argued that it is only one of a large number of such ratios.Lefebvre and Efremov considered the problem of double geometric progression and the golden section in the decay profiles of bursts[32]. They found that for bursts lasting less than 25 sec, if two significant peaks are observed in the power spectrum, the ratio of their centroid frequencies is approximately constant and equal to 1.59. They found that this ratio is very close to the golden section ratio of 1.618.In his paper, Smirnov[33] remarks that Kepler employed music proportions when he analyzed planetary movement parameters. There exists no contradiction in such a method. It is known that the same equations of oscillatory movement, for example, describe diverse physical phenomena. The mathematical basis of such a “musical” description of astronomical phenomena was the so-called “God’s proportion” or “golden section”. The golden section is found in bioengineering problems too. Bejan[34] claims that shapes with length/height ratios (L/H) close to 3/2 are everywhere and give the impression that they are being ‘designed’ to match the golden ratio (
, has been applied in diverse situations in art, architecture, and music, and although some have claimed that it represents a basic aesthetic proportion, others have argued that it is only one of a large number of such ratios.Lefebvre and Efremov considered the problem of double geometric progression and the golden section in the decay profiles of bursts[32]. They found that for bursts lasting less than 25 sec, if two significant peaks are observed in the power spectrum, the ratio of their centroid frequencies is approximately constant and equal to 1.59. They found that this ratio is very close to the golden section ratio of 1.618.In his paper, Smirnov[33] remarks that Kepler employed music proportions when he analyzed planetary movement parameters. There exists no contradiction in such a method. It is known that the same equations of oscillatory movement, for example, describe diverse physical phenomena. The mathematical basis of such a “musical” description of astronomical phenomena was the so-called “God’s proportion” or “golden section”. The golden section is found in bioengineering problems too. Bejan[34] claims that shapes with length/height ratios (L/H) close to 3/2 are everywhere and give the impression that they are being ‘designed’ to match the golden ratio ( = 1.618). In his article he showed that these shapes emerge as part of an evolutionary phenomenon that facilitates the flow of information from the plane to the brain, in accordance with the constructal law of generation and evolution of design in nature.The golden section is of interest to mathematicians who are interested in finding new construction methods. Kaplan et al. [36] constructed the golden ratio by using a bisector area of a trapezoid. Hofstetter[37] gave a simple five-step division of a segment into a golden section, using the ruler and rusty compass theorem. In a different study[38] he used the ruler and rusty compass theorem to construct three points, in four steps. Two of the distances between those points bear the golden ratio. A different way of construction is given by Tong and Kung[39]. They construct the golden ratio by using an area bisector of a trapezoid. In recent studies, there is further discussion of: crystals of golden proportions[43], golden ration in quantum mechanics[44] and about the effect of the 'golden ratio' on consumer behaviour[45].In this study, the efficiency of Carnot and endo-reversible heat engines and the coefficient of performance of Carnot heat pumps are cast with respect to the golden section ratio. The new expressions for efficiency are compared to Curzon and Ahlborn efficiency findings. Although the observed efficiencies were obtained as a result of pure mathematics, it is interesting to note that the relative differences in state-of-the-art efficiency of steam turbines[40] and of the combined gas cycles[41], differs only by a few percentage points.The order of this article is as follows: In section 2 the golden section Carnot heat engine and heat pump are analyzed. In section 3 the golden section endo-reversible heat engine with Newtonian heat transfer is considered. In section 4 a numerical example is given. Final conclusions and discussions are given in section 5.
= 1.618). In his article he showed that these shapes emerge as part of an evolutionary phenomenon that facilitates the flow of information from the plane to the brain, in accordance with the constructal law of generation and evolution of design in nature.The golden section is of interest to mathematicians who are interested in finding new construction methods. Kaplan et al. [36] constructed the golden ratio by using a bisector area of a trapezoid. Hofstetter[37] gave a simple five-step division of a segment into a golden section, using the ruler and rusty compass theorem. In a different study[38] he used the ruler and rusty compass theorem to construct three points, in four steps. Two of the distances between those points bear the golden ratio. A different way of construction is given by Tong and Kung[39]. They construct the golden ratio by using an area bisector of a trapezoid. In recent studies, there is further discussion of: crystals of golden proportions[43], golden ration in quantum mechanics[44] and about the effect of the 'golden ratio' on consumer behaviour[45].In this study, the efficiency of Carnot and endo-reversible heat engines and the coefficient of performance of Carnot heat pumps are cast with respect to the golden section ratio. The new expressions for efficiency are compared to Curzon and Ahlborn efficiency findings. Although the observed efficiencies were obtained as a result of pure mathematics, it is interesting to note that the relative differences in state-of-the-art efficiency of steam turbines[40] and of the combined gas cycles[41], differs only by a few percentage points.The order of this article is as follows: In section 2 the golden section Carnot heat engine and heat pump are analyzed. In section 3 the golden section endo-reversible heat engine with Newtonian heat transfer is considered. In section 4 a numerical example is given. Final conclusions and discussions are given in section 5.2. The Golden Section Carnot Heat Engine and Heat Pump
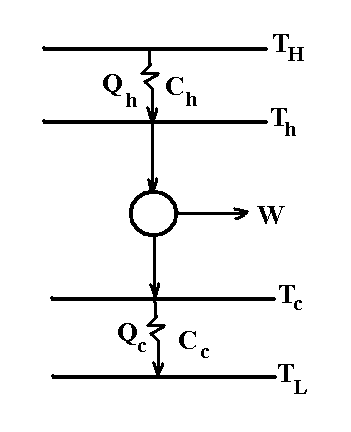
- Consider a Carnot heat engine that works between two heat reservoirs, a hot reservoir with a temperature of
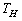 , and cold reservoir with a temperature of
, and cold reservoir with a temperature of 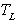 .
.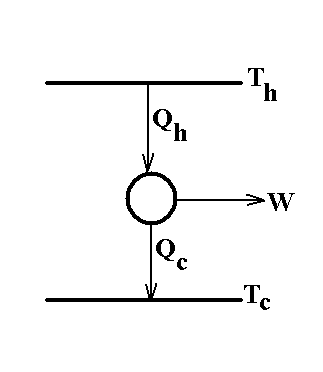 | Figure 1. Schematics of the Carnot heat engine operating between two heat reservoirs, the hot reservoir at 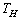 and the cold reservoir at and the cold reservoir at 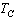 |
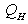 and the heat output from the engine is
and the heat output from the engine is 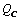 . The work output
. The work output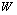 is calculated based on the energy equation and is given by:
is calculated based on the energy equation and is given by: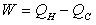 | (1) |
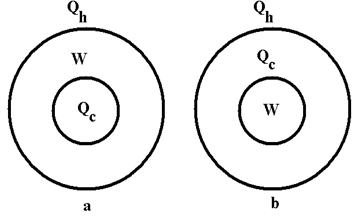 | Figure 2. The golden section division if the heat input 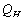 is done in two different ways: is done in two different ways: |
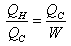 | (2) |
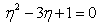 | (3) |
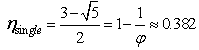 | (4) |
 is the single cycle of golden section Carnot heat engines cast in terms of the golden section ratio, and
is the single cycle of golden section Carnot heat engines cast in terms of the golden section ratio, and 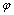 is the golden section ratio (
is the golden section ratio (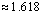 ).For the Carnot heat engine there are five physical quantities: the amount of heat input to the engine, the amount of heat rejected by the engine, the work output, and the reservoir's temperatures and efficiency. These quantities are related to each other with three equations: one for energy conservation, one for entropy conservation, and one for computing the efficiency definition. For a given value of efficiency, heat input, the cold reservoir temperature, and the two conservation equations, is it possible to solve for the other unknowns: the heat output, the work output, and the hot reservoir temperature. After some mathematical manipulation, the hot reservoir temperature is given by:
).For the Carnot heat engine there are five physical quantities: the amount of heat input to the engine, the amount of heat rejected by the engine, the work output, and the reservoir's temperatures and efficiency. These quantities are related to each other with three equations: one for energy conservation, one for entropy conservation, and one for computing the efficiency definition. For a given value of efficiency, heat input, the cold reservoir temperature, and the two conservation equations, is it possible to solve for the other unknowns: the heat output, the work output, and the hot reservoir temperature. After some mathematical manipulation, the hot reservoir temperature is given by: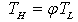 | (5) |
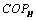 is given by:
is given by: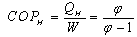 | (6) |
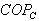 is given by:
is given by: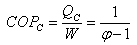 | (7) |
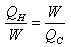 | (8) |
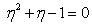 | (9) |
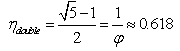 | (10) |
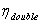 is the double cycle of golden section Carnot heat engines cast in terms of the golden section ratio.For this case the temperature of the hot reservoir is given by:
is the double cycle of golden section Carnot heat engines cast in terms of the golden section ratio.For this case the temperature of the hot reservoir is given by: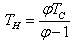 | (11) |
3. The Golden Section Endo-Reversible Heat Engine and Heat Pump
- In this section we consider an endo-reversible heat engine model.
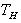 , and the cold reservoir at temperature
, and the cold reservoir at temperature 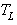 . The heat engine runs at finite rates, and heat input and heat rejection follow a Newtonian law. Heat input is given by:
. The heat engine runs at finite rates, and heat input and heat rejection follow a Newtonian law. Heat input is given by: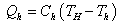 | (12) |
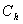 is the heat conductance at the hot side.Similarly, heat rejection is given by:
is the heat conductance at the hot side.Similarly, heat rejection is given by: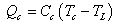 | (13) |
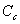 is the heat conductance at the cold side.Work output is given by equation 1, which is calculated from the energy equation:
is the heat conductance at the cold side.Work output is given by equation 1, which is calculated from the energy equation: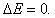 | (14) |
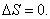 | (15) |
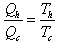 | (16) |
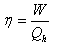 | (17) |
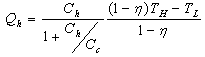 | (18) |
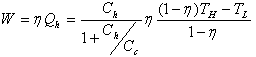 | (19) |
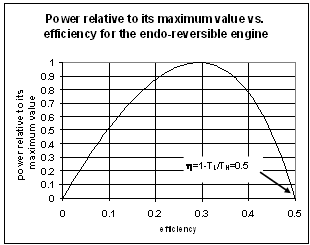 | Figure 4. shows the power output relative to its maximum value for the case of 50% Carnot efficiency |
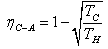 | (20) |
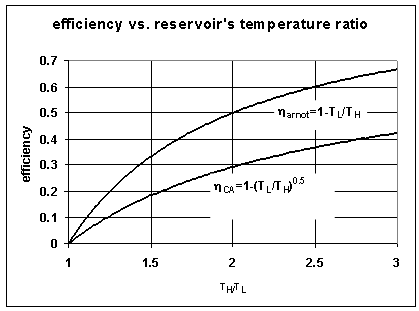 | Figure 5. Carnot efficiency and the Curzon and Ahlbon efficiency as a function of the reservoir's temperature ratio |
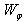 , (in the case of equal heat conductance values at both sides of the engine) is then given by:
, (in the case of equal heat conductance values at both sides of the engine) is then given by: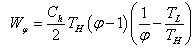 | (24) |
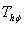 is given by:
is given by: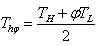 | (25) |
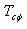 is given by:
is given by: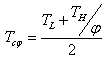 | (26) |
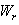 is defined as the ratio between the work output of the golden section endo-reversible heat engine. The maximum work output of the endo-reversible engine is given by:
is defined as the ratio between the work output of the golden section endo-reversible heat engine. The maximum work output of the endo-reversible engine is given by: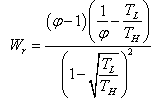 | (27) |
 which is the ratio between the working temperature at the hot side of the golden section endo-reversible heat engine and the working temperature of the endo-reversible heat engine at the hot side. This is given by:
which is the ratio between the working temperature at the hot side of the golden section endo-reversible heat engine and the working temperature of the endo-reversible heat engine at the hot side. This is given by: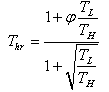 | (28) |
 which is the ratio between the working temperature at the cold side of the golden section endo-reversible heat engine and the working temperature of the endo-reversible heat engine at the cold side. This is given by:
which is the ratio between the working temperature at the cold side of the golden section endo-reversible heat engine and the working temperature of the endo-reversible heat engine at the cold side. This is given by: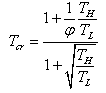 | (29) |
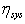 as defined in[12] is given by:
as defined in[12] is given by: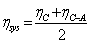 | (30) |
4. Numerical Example
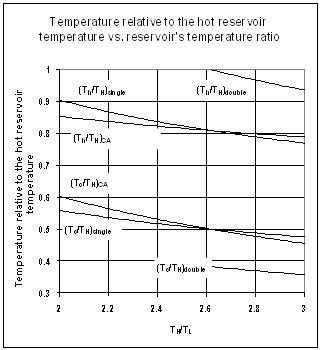
- In this section we consider a numerical example for illustration and comparison purposes. Consider a Carnot heat engine with a hot reservoir at 600K, which is a typical value of a Rankine cycle[42,46]. A Rankine cycle, with steam as the working fluid, has a limitation of the equation of state[12]. The consequences of such a limitation are reflected in the maximum temperature that may be achieved, and thus limit the maximum efficiency. On the other hand, the cold reservoir is at 300K, which is in principle the ambient temperature. For this case, the Carnot efficiency is 50%. The golden section efficiency (as given by equation 4) equals 38.2%, and the Curzon and Ahlborn efficiency (as given by equation 20) equals approximately 29.29%. The system efficiency (calculated from equation 30) is approximately 39.65%. Thus, the relative difference between the system efficiency and the golden section efficiency is approximately 3.6%.For the golden section Carnot heat engine, the hot side reservoir temperature, as estimated by equations 5 and 11, equals 484.4K for the single cycle and 785.4K for the double cycle, respectively.For steam parameters with supercritical temperature of 610℃[40], the endo-reversible heat engine predicts a working temperature at the hot side as 710K. A working temperature at the cold side is predicted to be 410K. On the other hand, the results predicted from the golden section endo-reversible heat engines are 693K (equation 25) and 428K (equation 26) respectively. Thus the relative differences fall in the range of approximately 2-4%. Finally, the work ratio (equation 27) predicts 85%. The golden section endo-reversible heat engine introduces only a 15% reduction of the maximum work output. For the double cycle golden section endo-reversible heat engine, the efficiency is at approximately 60%, at the price of significant reduction in power. In such a case, the heat engine is split into a bottoming cycle.
5. Conclusions and Discussion
- In this study a golden section Carnot heat engine and heat pump models were considered in section 2. Expressions for efficiency and for hot reservoir temperatures were observed and cast as a function of the golden section ratio. For the Carnot heat engines two cases were considered: a single cycle and a double cycle. The efficiency of the single cycle was observed to be 38.2%. The hot side temperature of the Carnot heat engine is predicted to be 484.4K based on a 300K cold reservoir. For the double cycle case, the golden section efficiency of the Carnot cycle is 61.8% with a 785.4K hot reservoir temperature.The golden section endo-reversible heat engine model was considered in section 3. The observed efficiency of the heat engine working between 600K and 300K heat reservoirs is 38.2%, which differs by about 3.6% relative to the system efficiency of 39.65% (which is given by equation 40). The working fluid temperatures for the golden section endo-reversible heat engine and the endo-reversible engine were calculated. The relative difference between them falls in the range 2-4% at the cost of 15% of the work output. Similar analysis was performed for the Carnot heat pump and expressions for the coefficients of performance for heating and cooling were given by equations 6 and 7.Although the golden section ratio is a pure mathematical issue, it is interesting to note that the observed efficiencies of the single cycle and double cycle differ by small amounts from the state of the art efficiencies of steam turbines and gas combined cycles. This can be seen from the studies of Wilfried[40] and Ishikawa et al. [41]. Wilfried[40] reports that state of the art of steam turbines (single cycle) with supercritical pressures and temperatures up to 610℃ reach higher cycle efficiencies. The improvement in efficiency is due to progress in materials technology (for casing, rotors, and turbine blades) and computers (CFD simulations). Optimizing the turbine blades led to reduced inner losses with 96% turbine efficiency. Ishikawa et al. [41] report that the system efficiency (net efficiency) could reach 43%. Gas turbine combined cycle power plants (double cycle) that mainly use MHI D, F, and G-type gas turbines are currently in operation in large numbers. Many similar installations are under construction or planned, both in Japan and abroad. The Ishikawa group analyzed the efficiency of the combined cycle plant with a 1,700℃ class gas turbine with inlet temperatures improved to 1,700℃. They then compared those findings to F-type and G-type plants with inlet temperatures of 1,500℃. They found that efficiencies in gas turbine combined cycle power plants had reached the level of 62% - 65% (LHV base). Moreover, these efficiencies were expected to remain at higher levels than the efficiency of conventional combined cycle plants.The golden section has been reported in the literature as a measure of beauty in different fields of science and nature. In this study the efficiency of heat engines evolved over many years to reach the level of the golden section ratio. The central question remains: Did heat engines actually reach the measure of beauty described as the golden section, or are the observed expressions of efficiency simply fortuitous?
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML