-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
International Journal of Arts
p-ISSN: 2168-4995 e-ISSN: 2168-5002
2011; 1(1): 1-22
doi:10.5923/j.arts.20110101.01

Geometrical Substantiation of Phi, the Golden Ratio and the Baroque of Nature, Architecture, Design and Engineering
Md. Akhtaruzzaman , Amir A. Shafie
Department of Mechatronics Engineering, Kulliyyah of Engineering, International Islamic University Malaysia, Kuala Lumpur, 53100, Malaysia
Correspondence to: Md. Akhtaruzzaman , Department of Mechatronics Engineering, Kulliyyah of Engineering, International Islamic University Malaysia, Kuala Lumpur, 53100, Malaysia.
| Email: |  |
Copyright © 2011 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Golden Proportion or Golden Ratio is usually denoted by the Greek letter Phi (φ), in lower case, which represents an irrational number, 1.6180339887 approximately. Because of its unique and mystifying properties, many researchers and mathematicians have been studied about the Golden Ratio which is also known as Golden Section. Renaissance architects, artists and designers also studied on this interesting topic, documented and employed the Golden section proportions in eminent works of artefacts, sculptures, paintings and architectures. The Golden Proportion is considered as the most pleasing to human visual sensation and not limited to aesthetic beauty but also be found its existence in natural world through the body proportions of living beings, the growth patterns of many plants, insects and also in the model of enigmatic universe. The properties of Golden Section can be instituted in the pattern of mathematical series and geometrical patterns. This paper seeks to represent a panoptic view of the miraculous Golden Proportion and its relation with the nature, globe, universe, arts, design, mathematics and science. Geometrical substantiation of the equation of Phi, based on the classical geometric relations, is also explicated in this study. Golden Ratio and its chronicle, concept of Golden Mean and its relations with the geometry, various dynamic rectangles and their intimacy with Phi, Golden Ratio in the beauty of nature, Phi ratio in the design, architecture and engineering are also presented in this study in a panoptical manner.
Keywords: Golden Ratio, Golden Section, Golden Mean, Golden Spiral, Phi, Geometrical Validation of Phi, Fibonacci Number, Phi in Nature, Equation of Phi
Cite this paper: Md. Akhtaruzzaman , Amir A. Shafie , Geometrical Substantiation of Phi, the Golden Ratio and the Baroque of Nature, Architecture, Design and Engineering, International Journal of Arts, Vol. 1 No. 1, 2011, pp. 1-22. doi: 10.5923/j.arts.20110101.01.
Article Outline
1. Instauration
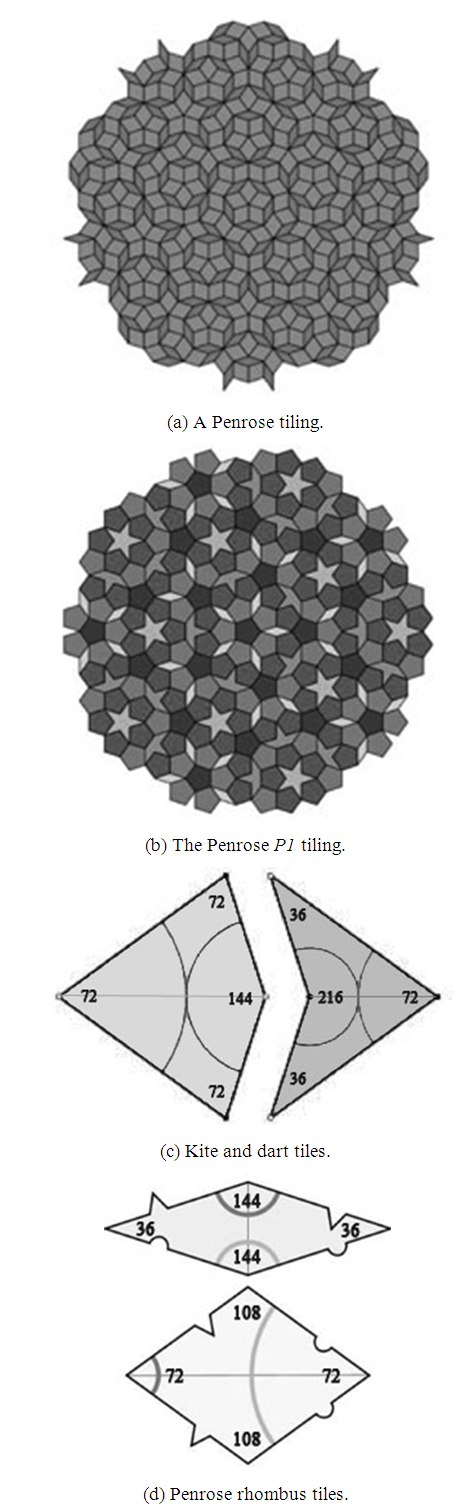
- The interrelation between proportion and good looks has made a lot of discussion in science because of the accidental occurrence of the shapes in various designs of objects like books, paintings, edifices and so on. The designs are approximated by a rectangle shaped such that the ratio of its length and height is equal to the ‘Golden Ratio,’ φ = (1 + 51/2)/2 = 1. 6180339887 (approx.). The ‘φ’ also called as the divine proportion, golden section, golden cut, golden ratio, golden mean etc. which is the result of dividing a segment into two segments (A + B) such that A/B = (A+B)/A = 1. 6180339887 (approx.) where A > B [1].The natural proportioning system provides the foundation of the work of many artists and designers. The proportion known as the Golden Mean has always existed in mathematics and in the physical universe and it has been of interest to mathematicians, physicists, philosophers, architects, artists and even musicians since antiquity. According to the great German mathematician Johannes Kepler (December 27, 1571 – November 15, 1630), geometry has two great treasures, theorem of Pythagoras and the division of a line into extreme and mean ratio [2]. In the early days of the 19th century it was suggested that the Greek letter ‘φ’ (Phi), the initial letters of Phidias’s name, should be adopted to designate the golden ratio [2]. In the medieval age and during the Renaissance, the ubiquity of ‘φ’ in mathematics aroused the involvement of many mathematicians. It is unknown exactly when the idea was first discovered and applied by mankind. It appears that the primitive Egyptian engineers may have used both Pi (π) and Phi (φ) in the structural design of the Great Pyramids. The Greeks based the design of the Parthenon (example of Doric architecture, the main temple of the goddess Athena built more than 400 years BC) on this proportion. Phidias, a Greek sculptor and mathematician (490-430 BC), studied Phi and applied this ratio in designing the sculptures of the Parthenon [2,4,5]. Plato (427-347 BC), in his views and understanding on natural science and cosmology presented in his Timaeus, one of his well-known dialogues, considered the golden section to be the most binding of all mathematical relationships and the key to the physics of the cosmos. In Elements, Euclid (325-265 BC) represented a line by dividing at the 0.6180399 point as the extreme and mean ratio. Afterwards the use of the term, Mean, appeared as Golden Mean to represent the ratio. He also proved the links of this number with the construction of a pentagram [2,6]. The Fibonacci Series was discovered, around 1200 AD, by Leonardo Fibonacci (1170-1250 AD) who was an Italian born mathematician. He found the interesting and mysterious properties of this numerical series latterly it is found that the series has a deep relation with Phi and the Golden Mean. The concept of this ratio was first called as the Divine Proportion in the early 1500's when Da Vinci provided his illustrations for a dissertation which was published by Luca Pacioli in 1509 and entitled as De Divina Proportione. This book contains drawings of the five Platonic solids. It is predicted that Da Vinci was the first person who called it the Sectio Aurea, which is Latin terms indicating the Golden Section. The Renaissance artists used the Golden Mean extensively in their paintings and sculptures to achieve balance and beauty. Leonardo Da Vinci used it to define all the fundamental proportions of his painting of The Last Supper, from the dimensions of the table, at which Christ and the disciples sat, to the proportions of the walls and windows in the background. Johannes Kepler (1571-1630 AD) who discover the elliptical nature of the orbits of the planets around the Sun also reflects the concept of the Divine Proportion. Martin Ohm (1792–1872 AD) who is believed to be the first man used the term ‘Goldener Schnitt’, Golden Section, to describe this proportion. The term Phi was not used before the 1900's until the American mathematician Mark Barr who used the Greek letter Phi to designate this proportion in his works. By this time the ubiquitous proportion was known as the Golden Mean, Golden Section and golden Ratio as well as the Divine Proportion. The proportion is said as Golden and Divine because of its unique properties to open the door of deeper understanding of beauty and spirituality of real world and universe.Phi is the first letter of Phidias, who used the golden ratio in his sculptures. The Greek equivalent to the letter φ is F which is the first letter of the word Fibonacci. Phi is also the 21st letter of the Greek alphabet, and 21 is one of numbers in the Fibonacci series. Not only that, the summation of the digits of 21 is 3 (2 + 1 = 3) which is also one of the numbers of the Fibonacci series. ‘Phi’ also contains three alphabets. Again 21 holds the eighth position of the series and the number 8 is also a member of the Fibonacci sequence. The characteristics of Phi have some interesting theological implications. The aesthetic primacy of the golden section was established empirically, and it was the very first topic of scientific psychological research as the new discipline emerged in the 19th century [15]. Fechner was the first person who fixed his analytical gaze upon this task as early as the 1860's. Since that time, it has been the focus of a number of research fields such as Structuralism, Gestalt psychology, Behaviourism, Social psychology, Psychiatry and Neuroscience at various points in time [15]. Phi continued to open new doors in the understanding of life, nature and the universe. It appeared in Roger Penrose's discovery of Penrose Tiles in the 1970's, which first allowed surfaces to be tiled in five-fold symmetry [37]. It appeared again in 1984 in the aluminium-manganese alloy (Al6Mn), known as quasi-crystals, which was newly discovered form of matter [37]. The relation between the Golden Ratio and the Black Holes is presented in 2011 by Nieto [39]. This study represents the black hole solution in higher dimensions where a sparkling relation is found with the Phi. Anthropomorphic Robot research is one of the interesting fields where the humanoid robot sizing can be established based on Golden Proportion to make the social robot more presentable and acceptable to the general public [16,34,40,41]. Golden Ratio also used in particle swarm optimization [42]. A recent study on ortho-cortex and para-cortex, two types of Cortex in Wool fibre, is conducted to have a better understanding on the relationship between the fibre structure and its properties where the fractal dimension of wool fibre shows the existence of Golden Mean in its structure [43]. A theoretical foundation of applying a new control law, the Golden Section Adaptive Control (GSAC) law, is established in recent analysis to control a specific aircraft [44]. The next section, section 2, of this writing represents a succinct review on the relation between the Golden Ratio and the Geometry, concept of various dynamic rectangles and their links with the Phi ratio. Section 3 provides the substantiation of the equation of Phi contingent upon the classical geometrical approach. Phi as the baroque of the natural beauty and natural enigma is presented in section 4 with some representative patterns of the natural phenomena. In section 5, the uses and presence of the golden proportion in various artefacts, arts, portrait, design, architectural works and engineering are briefly introduced in a panoptic manner. Finally, the section 6 abridges the paper with some positive and opposite concept of the relation between the beauty and the Golden Proportion.
2. Phi and Its Relation with Geometry
2.1. Concept of Golden Section
- For a line segment, golden section can be considered as a point where the line is divided into two sections containing a unique property such as the ratio between the bigger segment and the shorter segment should be equal to the ratio between the line and its bigger segment [10-15,26,33-37]. The ratio is approximately 1.6180339887 and is indicated by the Greek letter φ. If a line AC is considered according to Figure 1, the point B is its golden section where the line is divided into two sections p and q (AB = p and BC = q). According to the theory, the ratio of p and q is equal to the ratio between (p + q) and p where p > q. This relation can be represented by the following equation,
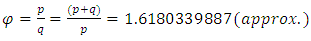 | (1) |
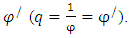 From the most ancient time it is often been claimed that the golden section is the most aesthetically pleasing point at which the line is sectioned. Consequently, the idea has been incorporated into many art works, architectural design and mathematical analysis.
From the most ancient time it is often been claimed that the golden section is the most aesthetically pleasing point at which the line is sectioned. Consequently, the idea has been incorporated into many art works, architectural design and mathematical analysis. | Figure 1. A line segment AC is divided in the golden section point B |
2.2. Concept of Golden Rectangle and its Construction Strategy
- A rectangle that is commonly associated with φ is the golden rectangle. It is a particular rectangle where the ratio between the length and width is exactly the same as the value of φ [13,14,15,37]. ABCD is a golden rectangle shown in Figure 2. The ratio between the two adjacent sides, AB and BC or CD and DA, is equal to the ratio between p and q or (p+q) and p. A straight line MN can be considered through the golden section of the ABCD that creates a square, ANMD, and a new smaller rectangle, MNBC, inside that golden rectangle. The side of the square is equal to the length of p and the new smaller rectangle having the adjacent sides equal to p and q (BC=MN=p and CM=BN=q) can be considered as the second level new smaller golden rectangle. Another straight line, IJ, also can be drawn between the two golden sections of the two sides AD and BC that will make another smallest square, MGJC, and another third level golden rectangle, GNBJ. This process can be continued for ever which will create smaller to smallest golden rectangles. The two lines MN and IJ intersect together at the point G and this intersection point is considered as the golden mean of the golden rectangle ABCD. Based on the different position of the golden section of a line, there can be at most four golden means in a golden rectangle. In Figure 2, the imaginary points G1, G2 and G3 are the other possible golden mean points of the golden rectangle, ABCD.
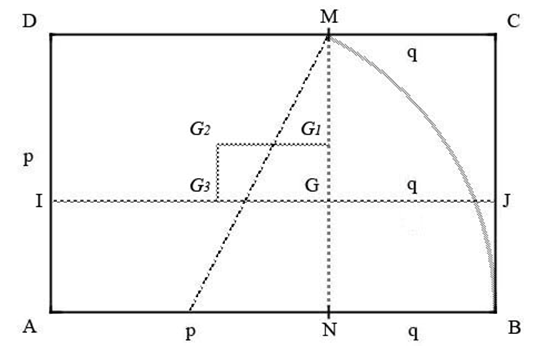 | Figure 2. Golden Rectangle, ABCD and the golden mean point G |
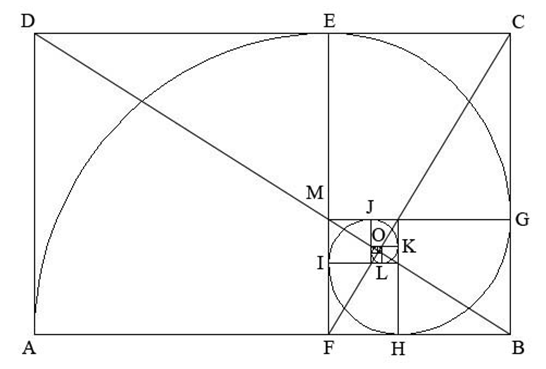 | Figure 3. Golden rectangle ABCD and golden spiral AEGHIJKLO |
2.3. Golden Triangles and Relations with Other Geometrical Patterns
- Golden triangle is an isosceles triangle having 72° angle at the base and 36° angle at its zenith [1,15] or 36° angle at base and 108° angle at the apex. Figure 4 shows the two types of golden triangle ABC and XYZ. The ratio between any of its legs and its base is exactly same as the value of φ. Based on Figure 4 (a) and (b), Equation (1) can be written as,
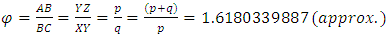 | (2) |
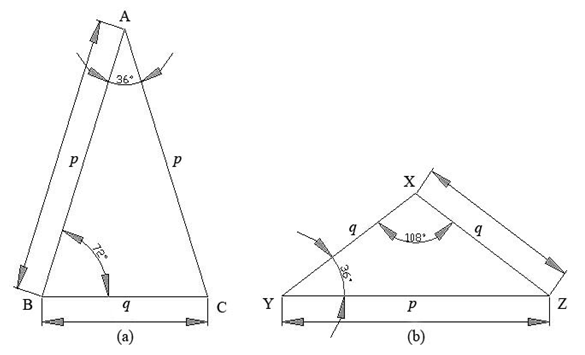 | Figure 4. Two different types of golden triangle (a) ABC and (b) XYZ |
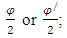
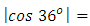
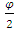 and
and 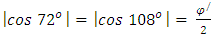 . There are many examples in natural world where φ is intimately related with the shape of regular pentagon or pentagram. These pentagon and pentagram are possible to characterized using the golden triangle. The concept of golden triangle is very important because of the pentagonal symmetry in nature has often taken as an initial step to investigate the mystery of φ in the universe [15]. The decagram and decagon also yield a series of golden triangles by connecting the centre point with any two adjacent edges [1,2,15].
. There are many examples in natural world where φ is intimately related with the shape of regular pentagon or pentagram. These pentagon and pentagram are possible to characterized using the golden triangle. The concept of golden triangle is very important because of the pentagonal symmetry in nature has often taken as an initial step to investigate the mystery of φ in the universe [15]. The decagram and decagon also yield a series of golden triangles by connecting the centre point with any two adjacent edges [1,2,15]. | Figure 5. A series of golden triangles construct the Regular Pentagon, Pentagram, Regular Decagon and Decagram |
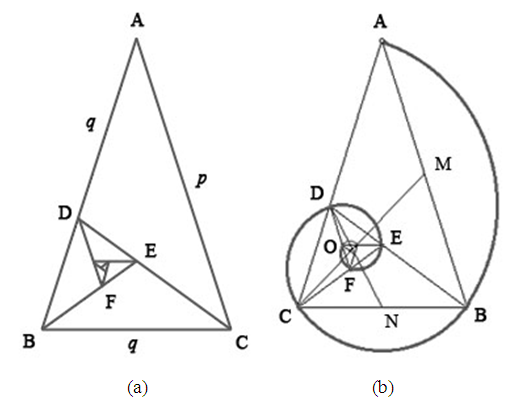 | Figure 6. Golden spiral formed on the whirling golden triangle |
2.4. Golden Angle and Golden Ellipse
- A circle can be divided into two arcs in the proportion of the golden ratio, where the smaller arc marks a central angle of 137.5 degrees which is considered as golden angle. A Golden Section Ellipse is an ellipse drawn inside a Golden Section Rectangle where it has the same proportion of the major and minor axis as 1:1.618. A Golden Triangle is possible to draw inscribing in a Golden Ellipse that inscribes in a Golden Rectangle [2,13,15].
2.5. Concept on Dynamic Rectangles
- Based on the rational and irrational number of the proportion, a rectangle can be considered as either a static rectangle or a dynamic rectangle. Static rectangles have ratios of rational fractions such as 1/2, 2/3, 3/3, 3/4 etc. Dynamic rectangles are the rectangles with ratios of irrational fractions like √2, √3, √5, φ (golden section) etc. [1-3]. Static rectangles do not produce a series of visually pleasing ratios of surfaces while subdividing. On the other hand, dynamic rectangles produce an endless amount of visually pleasing harmonic subdivisions and surface ratios. There is a great intimacy between the √5 and φ both in mathematics and geometry. √2 rectangles possess an especial property, like Golden Rectangle, of being endlessly subdividing into proportionally smaller rectangles. It is possible to get two smaller √2 rectangles while dividing into half, dividing into forth resulting four smaller √2 rectangles and so on. The proportions of the √2 rectangle are approximately 1:1.42. √3, √4 and √5 rectangles also can be subdivided into three √3 rectangles, four √4 rectangles and five √5 rectangles respectively where the dividing process can be continued endlessly [2,3]. The proportions of the √3, √4 and √5 rectangles are approximately 1:1.732, 1:2 and 1:2.236 respectively. Any of these rectangles can easily be drawn depending on its immediate antecedent such as √5 rectangles can be formed easily from √4 rectangles, √4 rectangles from √3 rectangles etc. Drawing a √2 rectangle depends on a square which also can be considered from √1 rectangle. Figure 7 shows the various dynamic rectangles and their construction strategies.Beginning with a square having a diagonal BD, shown in Figure 7 (a), a √2 rectangle can be constructed. An arc DF having the radios BD touches at the point F on the baseline of the squire ABCD. A new rectangle with the point F can be formed as ABFE which is considered as a √2 rectangle. Similarly, another diagonal, BE, can be drawn that can be considered as the radios of the arc EG which is touching at the point G on the base line of the √2 rectangle. Now the new rectangle ABGH is obtained which is the √3 rectangle. The same procedure will construct the √4 and √5 rectangles as shown in Figure 7 (a).
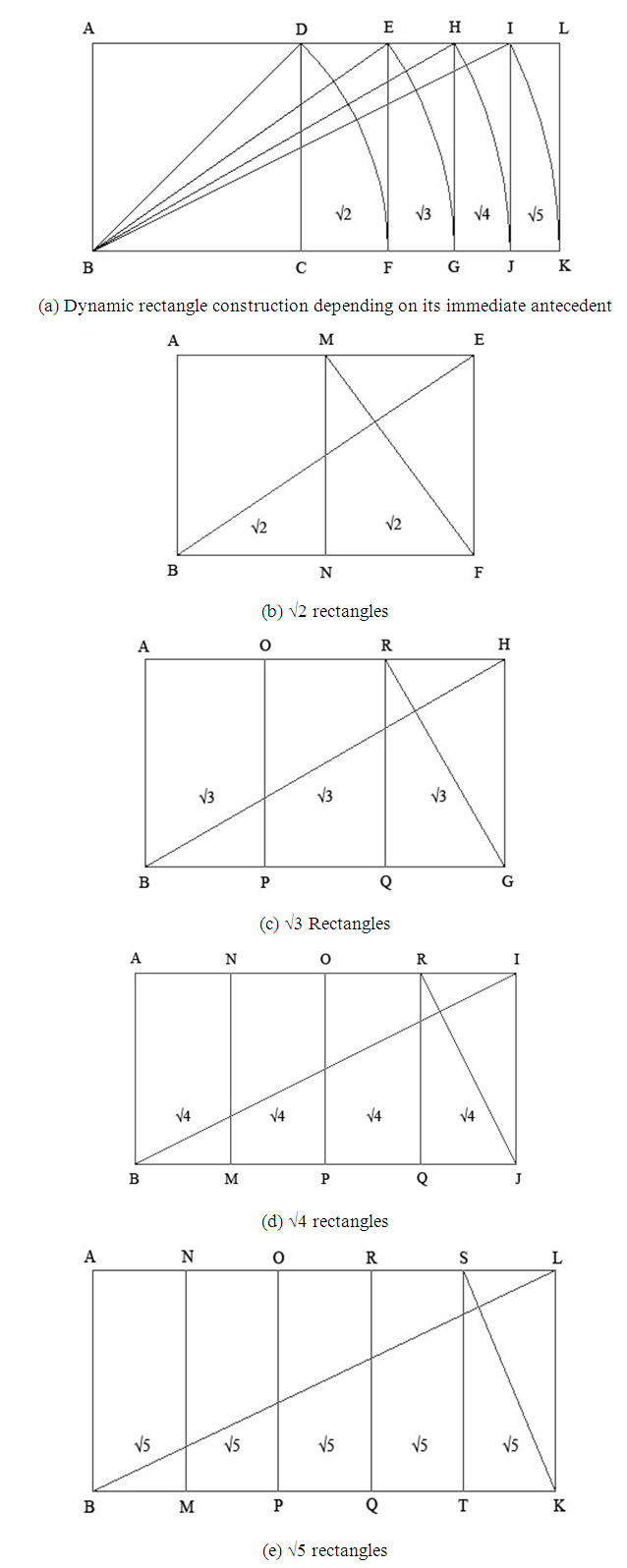 | Figure 7. Representation and construction of various dynamic rectangles |
3. Geometrical Substantiation of the Equation of Phi
- Phi is one of the great treasures of Geometry. As shown in Equation (3), the value of Phi has a close relation with √5 [1,28,29]. The same concept also can be applied to draw a golden rectangle which could be the geometrical proof of the equation of Phi.
 | (3) |
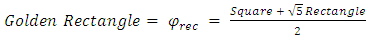 | (4) |
 | Figure 8. (a) A square, (b) a Root 5 rectangle and (c) Golden Rectangle construction based on the equation of Phi |
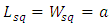 | (5) |
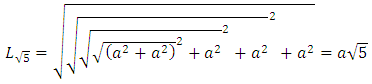 | (6) |
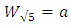 | (7) |
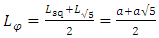 | (8) |
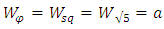 | (9) |
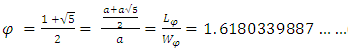 | (10) |
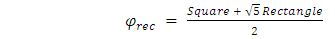 | (11) |
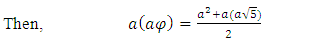 | (12) |
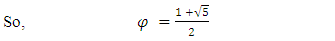 | (13) |
4. Golden Section and the Beauty of Nature
- In 12th century, the Leonardo Fibonacci questioned about the population growth of the rabbits under ideal circumstances, such as no predators to eat them or no dearth of food and water that would affect the growth rate. The answer of the question is the Fibonacci Sequence of Numbers, also known as Fibonacci Numbers, that starts from 1 and each new number of the series is simply the sum of the previous two numbers. So, the second number of the series is also 1, the sum of the previous 1 and 0 of the series. The sequence of the number looks like the series bellow.0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, ……………etc.Fibonacci numbers are said as one of the Nature's numbering systems because of its existence not only in the population growth of rabbits, but also everywhere in Nature, from the leaf arrangements in plants to the structures in outer space. The special proportional properties of the golden section have a close relationship with the Fibonacci sequence. Any number of the series divided by the contiguous previous number approximates 1.618, near to the value of φ.
 | Figure 10. Passionflower (Passiflora Incarnata) from the back (a) and front (b) having the examples of Fibonacci Numbers in nature |
 | Figure 11. (a) Romanesco Brocolli having the pattern of Golden Spiral, (b) Cauliflower having a shape of a pentagon |
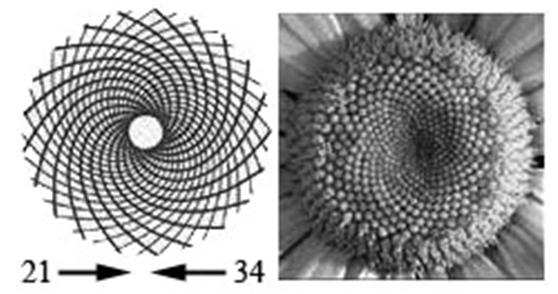 | Figure 13. Spiral arrangement of the seed florets of a Sunflower |
 | Figure 14. Appearance of golden spiral in nature (a) Orange petals seed florets, (b) Sunflower seed florets, (c) Pine Cones, (d) Broccoli, (e) Golden Ratio flower and (f) Petals of a Rose [38] |
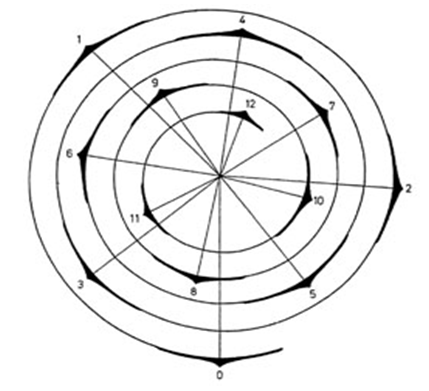 | Figure 15. Loosely distributed leaf’s structure where the successive leaves in the spiral are numbered and lined from the centre of the spiral [18] |
 | Figure 17. Some various Cactuses are showing the existence of the Golden Spiral in their various growth patterns [18,50] |
 | Figure 20. Golden Section appears in (a) ant’s body parts, (b) peacock’s feather and (c) natural design of a butterfly [17,47,48] |
 | Figure 21. Some example of the physical universe where Golden Section properties are exists [47,48] |
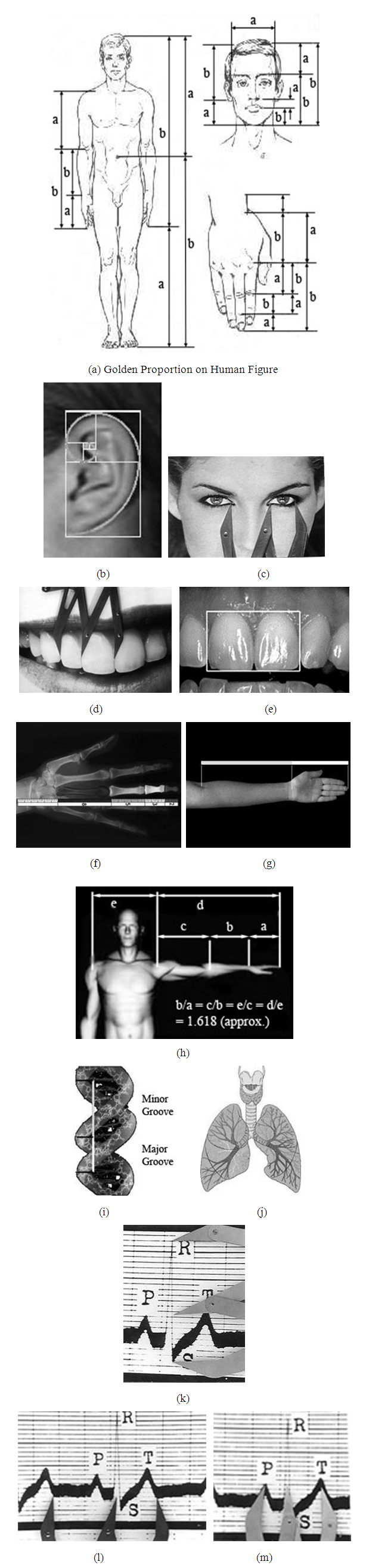
 [Surah At-Tin (95), Verse 8]. Meaning: We have indeed created human in the best of modules. It is known that the Arabic text direction is from right to left. There are exactly 26 characters in this sentence and the word “Insana”
[Surah At-Tin (95), Verse 8]. Meaning: We have indeed created human in the best of modules. It is known that the Arabic text direction is from right to left. There are exactly 26 characters in this sentence and the word “Insana”  means ‘man’ or ‘human’. This verse also has the Golden proportion where the word “Insana” comes at the golden mean of the sentence. The 26 characters can be divided into two sections p and q. The left section p has 16 characters started from the word “Insana” and q has 10 characters from the beginning to that word. The ratio between p and q is 1.6 which is closer to the golden number 1.618... Indeed, Quran is a miracle for its eloquence in language, for applicability and relevance of its verses in all spheres of human life, for its inimitable verses and in many other aspects. It does not need to prove as scientific, rather we need to guide by it.The relationship of golden section is observed on the design of the human body shape and structure. It consists of one trunk, one head, one heart etc. Many parts of the body are in pair like arms, legs, eyes, buds. Legs and arms consist of three parts. Human fingers consist of three phalanxes, main, mean and nail. The length of all phalanxes of each finger relates to each other according to the rule of golden proportion. There are five appendages to the torso, the arms, legs and a head; five appendages on each of these, five fingers on hands, foot and five openings on the face. There exist five senses as sight, sound, touch, taste and smell. Five is a number of the Fibonacci series and the golden section is also computed using five, as shown in Equation (3). Many researchers of the human body mathematical regularities inscribed man into a pentagram. Such model was reflected in Leonardo da Vince and Durer's constructions. Again, hand consists of three main parts: wrists, metacarpus and fingers. Human arm together with fingers consists of eight parts. Eight bones enter to the wrist structure which is connected with five metacarpal bones forming the basis of the palm. Five fingers are connected to metacarpal bones. Human has 12 pairs of ribs and sometimes it is claimed (without any strong evidence) that in the past the man had 13 pairs of ribs. Facial, middle ears and throat consists of total 21 bones as 14, 6 and 1 respectively. Human backbone with the skull consists of 34 bones, 8 Crania (skull), 24 Vertebrae, one Sacrum and one Coccyx. The total number of 55 (21 + 34 = 55) bones compound together to build up the base column of human body structure. All of these numbers 1, 2, 3, 5, 8, 13, 21, 34 and 55 are the numbers of the Fibonacci series. Basically, it is necessary to do research on the roots of the natural laws deeper and deeper to establish the relation with the golden proportion.Dr. Stephen Marquardt, an eminent Oral surgeon in California, discovered that the height of the central incisor is in the Golden Proportion to the width of the two central incisors [17]. This revelation has offered solutions to a host of dental aesthetic problems. The Golden Proportion grids show the inter-tooth relationship between the eight teeth of the anterior aesthetic segment whereas the rectangle confirms the width of the incisors, related to their height [17]. The combination of grid and rectangle will mutually confirm the aesthetic solution with a certainty that it will look attractive and natural. These grids explained in the paper “Dental aesthetics and the golden proportion” are complementary to the Golden Proportion rectangle. The combination of the two gives a powerful tool to confidently determine good aesthetics. The four front teeth, from central incisor to premolar are the most significant part of the smile and they are in the Golden Proportion to each other. Dr Mc Arthur 1985 wrote an article "Maxillary and Mandibular Teeth Widths" in which he explained that the average ratio of upper central incisor to lower central incisor is 1.62. Shoemaker in 1987 wrote a series of articles promoting the use of the Golden Proportion as an adjunct to cosmetic Dentistry. Amoric (1989) in his article, "Le nombre d'or", showed many Golden Proportions in cephalometric tracings at various stages of facial growth and also included geometrical propositions. The Annals of Plastic Surgery 1989 include a fascinating study by Kawakami et al. who investigated the Golden Proportion balance between eyes, nose and mouth in the facial appearance of typical Japanese individuals and comparing the ratios to Caucasians, each ratio was then used for pre and post-operative aesthetic analysis using Moire' topography. Dr Jack Preston, in 1993, was influenced by the studies of Stephen Marquardt who developed a Golden Proportion Pentagon Grid for Facial plastic surgery. Dr Yosh Jefferson, in 1996, illustrates an article in the Journal of General Orthodontics with many Golden Proportion diagrams and computer generated photographs giving an ideal picture of the whole head. His work was also supported with cephalometric tracings.It was also found that the human heart beats are in the Golden Proportion rhythm. Figure 22 (j), (k) and (l) show the Golden Proportion gauge on Electrocardiogram (ECG) tracings of a normal heart. The DNA cross-section is also based on Phi ratio. A decagon is possible to draw from a cross-sectional view from the top of the DNA double helix. A decagon is in essence two pentagons, with one rotated by 36 degrees from the other. So, each spiral of the double helix must trace out the shape of a pentagon. The DNA molecule is also based on the Golden section. It measures 34 angstroms long and 21 angstroms wide for each full cycle of its double helix spiral model where 34 and 21 are the numbers in the Fibonacci series and their ratio is 1.6190476, closer to the ratio of Phi, 1.6180339….
means ‘man’ or ‘human’. This verse also has the Golden proportion where the word “Insana” comes at the golden mean of the sentence. The 26 characters can be divided into two sections p and q. The left section p has 16 characters started from the word “Insana” and q has 10 characters from the beginning to that word. The ratio between p and q is 1.6 which is closer to the golden number 1.618... Indeed, Quran is a miracle for its eloquence in language, for applicability and relevance of its verses in all spheres of human life, for its inimitable verses and in many other aspects. It does not need to prove as scientific, rather we need to guide by it.The relationship of golden section is observed on the design of the human body shape and structure. It consists of one trunk, one head, one heart etc. Many parts of the body are in pair like arms, legs, eyes, buds. Legs and arms consist of three parts. Human fingers consist of three phalanxes, main, mean and nail. The length of all phalanxes of each finger relates to each other according to the rule of golden proportion. There are five appendages to the torso, the arms, legs and a head; five appendages on each of these, five fingers on hands, foot and five openings on the face. There exist five senses as sight, sound, touch, taste and smell. Five is a number of the Fibonacci series and the golden section is also computed using five, as shown in Equation (3). Many researchers of the human body mathematical regularities inscribed man into a pentagram. Such model was reflected in Leonardo da Vince and Durer's constructions. Again, hand consists of three main parts: wrists, metacarpus and fingers. Human arm together with fingers consists of eight parts. Eight bones enter to the wrist structure which is connected with five metacarpal bones forming the basis of the palm. Five fingers are connected to metacarpal bones. Human has 12 pairs of ribs and sometimes it is claimed (without any strong evidence) that in the past the man had 13 pairs of ribs. Facial, middle ears and throat consists of total 21 bones as 14, 6 and 1 respectively. Human backbone with the skull consists of 34 bones, 8 Crania (skull), 24 Vertebrae, one Sacrum and one Coccyx. The total number of 55 (21 + 34 = 55) bones compound together to build up the base column of human body structure. All of these numbers 1, 2, 3, 5, 8, 13, 21, 34 and 55 are the numbers of the Fibonacci series. Basically, it is necessary to do research on the roots of the natural laws deeper and deeper to establish the relation with the golden proportion.Dr. Stephen Marquardt, an eminent Oral surgeon in California, discovered that the height of the central incisor is in the Golden Proportion to the width of the two central incisors [17]. This revelation has offered solutions to a host of dental aesthetic problems. The Golden Proportion grids show the inter-tooth relationship between the eight teeth of the anterior aesthetic segment whereas the rectangle confirms the width of the incisors, related to their height [17]. The combination of grid and rectangle will mutually confirm the aesthetic solution with a certainty that it will look attractive and natural. These grids explained in the paper “Dental aesthetics and the golden proportion” are complementary to the Golden Proportion rectangle. The combination of the two gives a powerful tool to confidently determine good aesthetics. The four front teeth, from central incisor to premolar are the most significant part of the smile and they are in the Golden Proportion to each other. Dr Mc Arthur 1985 wrote an article "Maxillary and Mandibular Teeth Widths" in which he explained that the average ratio of upper central incisor to lower central incisor is 1.62. Shoemaker in 1987 wrote a series of articles promoting the use of the Golden Proportion as an adjunct to cosmetic Dentistry. Amoric (1989) in his article, "Le nombre d'or", showed many Golden Proportions in cephalometric tracings at various stages of facial growth and also included geometrical propositions. The Annals of Plastic Surgery 1989 include a fascinating study by Kawakami et al. who investigated the Golden Proportion balance between eyes, nose and mouth in the facial appearance of typical Japanese individuals and comparing the ratios to Caucasians, each ratio was then used for pre and post-operative aesthetic analysis using Moire' topography. Dr Jack Preston, in 1993, was influenced by the studies of Stephen Marquardt who developed a Golden Proportion Pentagon Grid for Facial plastic surgery. Dr Yosh Jefferson, in 1996, illustrates an article in the Journal of General Orthodontics with many Golden Proportion diagrams and computer generated photographs giving an ideal picture of the whole head. His work was also supported with cephalometric tracings.It was also found that the human heart beats are in the Golden Proportion rhythm. Figure 22 (j), (k) and (l) show the Golden Proportion gauge on Electrocardiogram (ECG) tracings of a normal heart. The DNA cross-section is also based on Phi ratio. A decagon is possible to draw from a cross-sectional view from the top of the DNA double helix. A decagon is in essence two pentagons, with one rotated by 36 degrees from the other. So, each spiral of the double helix must trace out the shape of a pentagon. The DNA molecule is also based on the Golden section. It measures 34 angstroms long and 21 angstroms wide for each full cycle of its double helix spiral model where 34 and 21 are the numbers in the Fibonacci series and their ratio is 1.6190476, closer to the ratio of Phi, 1.6180339…. 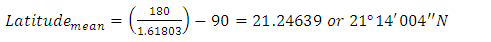 | (11) |
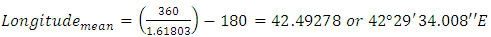 | (12) |
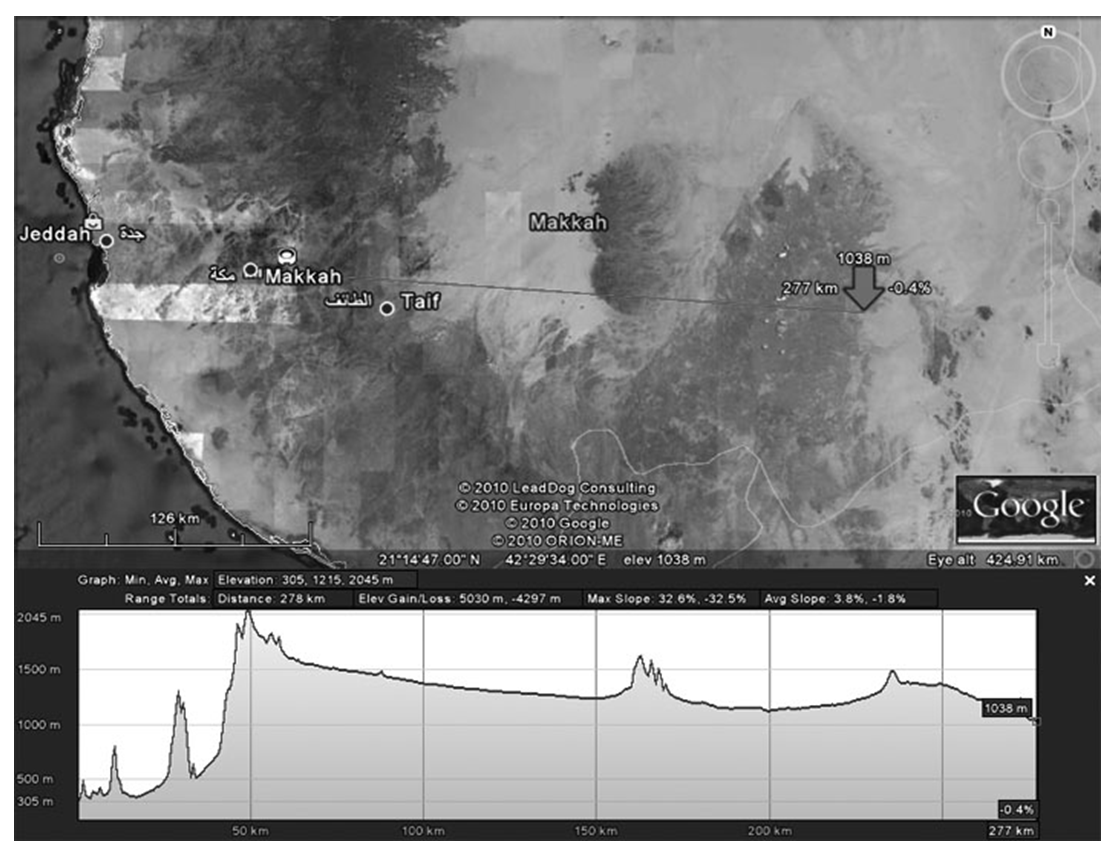 | Figure 23. Google Earth image indicating the latitude and longitude of Mecca and Golden Mean point of the Globe |
 Meaning is, “Lo! The first Sanctuary appointed for mankind was that at Mecca, a blessed place, guidance to the people.” The total number of all letters of this verse is 47. Calculating the golden ratio of total letters, it is clear that the word of Mecca is implied at (47 / 1.618) = 29. There are 29 letters from the beginning of the verse till the word,
Meaning is, “Lo! The first Sanctuary appointed for mankind was that at Mecca, a blessed place, guidance to the people.” The total number of all letters of this verse is 47. Calculating the golden ratio of total letters, it is clear that the word of Mecca is implied at (47 / 1.618) = 29. There are 29 letters from the beginning of the verse till the word, 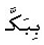 which indicates the Mecca and contains three characters itself.
which indicates the Mecca and contains three characters itself. 5. Golden Ratio in Design, Architecture and Engineering
- If the relative ratio is 1.618 for the components of any structure, the form will be convenient to Golden Ratio, says as the perfect design. One of the 5 platonic solids, dodecahedron, is described by Plato in the "The Phaedo" (110 B.) where he refers to a ball having twelve pentagonal faces. This was the precursor to the design of the modern football, made with a various number of pentagons as shown in Figure 24 (b). Golden ratio is also used in the design of violins, guitars and even in the design of high quality speaker wire. Le Corbusier, one of the famous architects, also represented the divine proportion onto his design, Chaise Longue in 1929, shown in Figure 24 (h). The proportion of the chaise relates to the harmonic subdivision of a golden rectangle where the width of the rectangle becomes the diameter of the arc that is the frame of the chaise [1]. Plywood Chair, designed by Charles Eames in 1946, also reflects the application of the golden ratio in its design strategies [1]. The chair back fits perfectly into a golden section rectangle.
 | Figure 26. (a) The Last Supper, (b) Monalisa Painting, (c) Bionic Man, (d) Leonardo's unfinished "St. Jerome", and (e) Salvador Dalí’s painting The Sacrament of the Last Supper [1,4,36,47,48] |
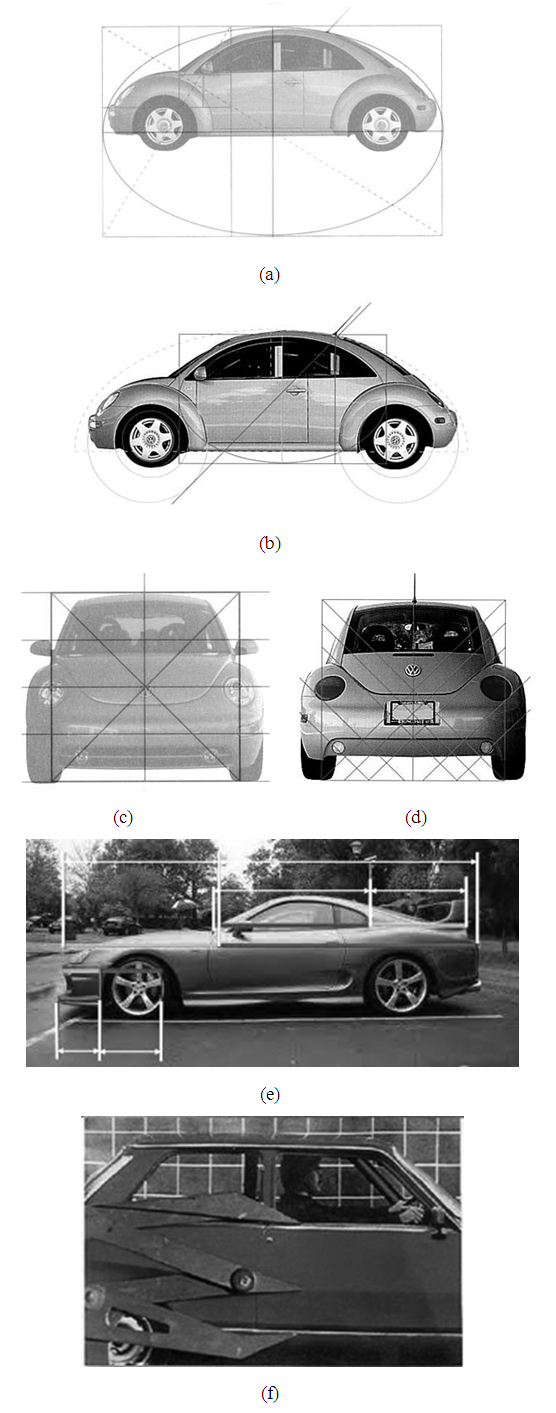 | Figure 27. Golden Ratio based design of cars, (a), (b), (c) and (d) Volkswagen Beetle, (e) Toyota Supra, and (f) Golden Section appears on a car’s door [1,47,48] |
6. Conclusions
- Using Fibonacci numbers, the Golden Ratio becomes a golden spiral, that plays an enigmatic role everywhere in the nature such as in shells, pine cones, the arrangement of seeds in a sunflower head and even galaxies. Adolf Zeising, a mathematician and philosopher, while studying the natural world, saw that the Golden Ratio is operating as a universal law. On the other hand, some scholars deny that the Greeks had any aesthetic association with golden ratio. Midhat J. Gazale says that until Euclid the golden ratio's mathematical properties were not studied. In the “Misconceptions about the Golden Ratio”, Dr. George Markowsky also discussed about some misconceptions of the properties and existence golden ratio [24] in various structures and design. Basically the Golden Ratio should not be considered as a convention to all circumstances like a law of nature but it needs deeper study and analysis to establish the relation with the ratio as it is a curiosity of researchers to fulfil the demand of this field of research. Some group of researchers in 1991 found an interesting rule in the decay profile of the RB type II Bursts that follows the golden ratio [27]. Y.H. Chan and S.A.R. Abu-Baker used a new strategy called Modified Golden Ratio (MGR) and designed an algorithm for face boundary refinement and face extraction [30]. Some other researchers also used the ratio to detect the face region in digital images [31]. Micha Hofri and Zvi Rosberg was designed a protocol named as Golden Ratio Control Policy for Multiple Access Channel Network and achieved the cost closer to the lower bound for realistic parameters [32]. Qing Xue and Phillip Sheu applied the golden section search method to find a set of collision free optimal paths for mobile robots [33]. In recent years the research on humanoid robotic platform is spreading rapidly where some researchers suggest that the golden ratio based analysis and designed can be considered for the design of Android structure [34,40,41,44-46].Basically, this study represents a qualitative review on Golden Proportion from ancient time to the present. The study also represents the mystery of various geometrical patterns and various dynamic rectangles. The proof of the equation of Phi based on the classical geometrical approach is also illustrated in this paper. Mainly the paper draws an extensive review on natural and artificial world to find out the relations with the Phi as the Golden and Devine Ratio.
ACKNOWLEDGEMENTS
- The authors would like to thank their honourable parents. They also would like to express their appreciations to the Ministry of Higher Education (MOHE), Malaysia, Research Management Centre (RMC), IIUM and Kulliyyah of Engineering, (KOE), IIUM, Malaysia.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML