-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
Architecture Research
2012; 2(3): 20-26
doi: 10.5923/j.arch.20120203.01
Effect of Irregular Configurations on Seismic Vulnerability of RC Buildings
Ravikumar C M1, Babu Narayan K S1, Sujith B V2, Venkat Reddy D1
1Department of Civil Engineering, National Institute of Technology, Surathkal, 575025, India
2cmravibdt@gmail.com, sujithbv@gmail.com
Correspondence to: Ravikumar C M, Department of Civil Engineering, National Institute of Technology, Surathkal, 575025, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
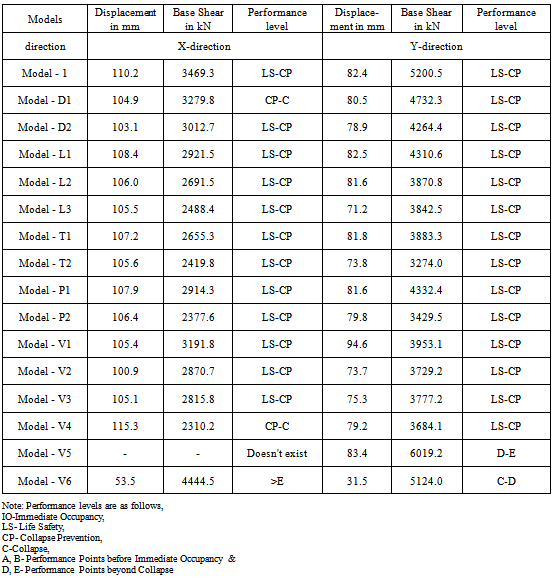
Many buildings in the present scenario have irregular configurations both in plan and elevation. This in future may subject to devastating earthquakes. In case, it is necessary to identify the performance of the structures to withstand against disaster for both new and existing one. The present paper made an attempt to study two kinds of irregularities in the building models namely plan irregularity with geometric and diaphragm discontinuity and vertical irregularity with setback and sloping ground. These irregularities are created as per clause 7.1 of IS 1893 (part1)2002 code. In Oder to identify the most vulnerable building among the models considered, the various analytical approaches are performed to identify the seismic demands in both linear and nonlinear way. It is also examined the effect of three different lateral load patterns on the performance of various irregular buildings in pushover analysis. This study creates awareness about seismic vulnerability concept on practicing engineers.
Keywords: Seismic, Irregularities, Pushover, Non-linear
Article Outline
1. Introduction
- Earthquakes are the most unpredictable and devastating of all natural disasters, which are very difficult to save over engineering properties and life, against it. Hence in order to overcome these issues we need to identify the seismic performance of the built environment through the development of various analytical procedures, which ensure the structures to withstand during frequent minor earthquakes and produce enough caution whenever subjected to major earthquake events. So that can save as many lives as possible. There are several guidelines all over the world which has been repeatedly updating on this topic. The analysis procedure quantifying the earthquake forces and its demand depending on the importance and cost, the method of analysing the structure varies from linear to non linear. The behaviour of a building during an earthquake depends on several factors, stiffness, adequate lateral strength, ductility, simple and regular configurations. The buildings with regular geometry and uniformly distributed mass and stiffness in plan as well as in elevation suffer much less damage compared to irregular configurations. But nowadays need and demand of the latest generation and growing population has made the architects or engineers inevitable towards planning of irregular configurations. Hence earthquake engineering hasdeveloped the key issues in understanding the role of building configurations.
1.1. Objective of the Study
- To obtain the Seismic performances of different irregular buildings located in severe earthquake zone (V) of India, and also identify the most vulnerable building among them.
1.2. Scope of the Study
- The Present work is focused on the study of Seismic demands of different irregular R.C buildings using various analytical techniques for the seismic zone V (hard rock) of India. The configuration involves plan irregularities such as diaphragm discontinuity, re-entrant corners and vertical irregularities such as geometrical irregularity, buildings resting on sloping ground. The performance was studied in terms of time period, base shear, lateral displacements, storey drifts and eccentricity in linear analysis using a code – IS1893 (Part 1):2002 .Whereas the performance point and hinge status in Non linear analysis using ATC40. Also an attempt was made in pushover analysis to identify the correct lateral load pattern when different irregular buildings were considered. The entire modelling, analysis and design was carried out by using ETABS 6.0 nonlinear version software.
2. Illustrative Examples
- The Layout of plan having 5X4 bays of equal length of 5m Figure 1. The buildings considered are Reinforced concrete ordinary moment resisting frame building of three storeys with different irregular configurations. Here stiffness of the infill is neglected in order to account the nonlinear behaviour of seismic demands. The storey height is kept uniform of 3m for all kind of building models which are as below,
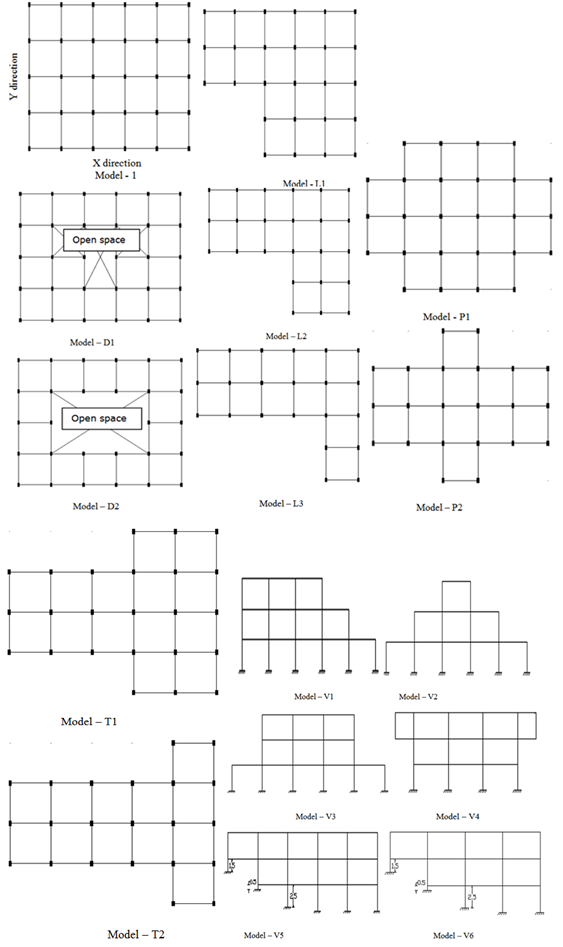 | Figure 1. Building Models |
3. Analysis Methods
- Analysis methods are broadly classified as linear static, linear dynamic, nonlinear static and nonlinear dynamic methods. In these the first two methods are suitable when the structural loads are small and no point, the load will reach to collapse load and are differs in obtaining the level of forces and their distribution along the height of the structure. Whereas the non- linear static and non-linear dynamic analysis are the improved methods over linear approach. During earthquake loads the structural loading will reach to collapse load and the material stresses will be above yield stresses. So in that case material nonlinearity and geometrical nonlinearity should be incorporated into the analysis to get better results. These methods also provide information on the strength, deformation and ductility of the structures as well as distribution of demands.
3.1. Equivalent Static Method
- Equivalent static method of analysis is a linear static procedure, in which the response of building is assumed as linearly elastic manner. The analysis is carried out as per IS1893-2002 (Part 1) [6]
3.2. Response Spectrum Method
- Linear dynamic analysis of the building models is performed using ETABS. The lateral loads generated by ETABS correspond to the seismic zone V and 5% damped response spectrum given in IS 1893-2002 (Part 1) [6]. The fundamental natural period values are calculated by ETABS, by solving the eigenvalue problem of the model. Thus, the total earthquake load generated and its distribution along the height corresponds to the mass and stiffness distribution as modelled by ETABS.
3.3 Pushover Analysis
- Pushover analysis is one of the methods available to understand the behaviour of structures subjected to earthquake forces. As the name implies, it is the process of pushing horizontally with a prescribed loading pattern incrementally until the structure reaches a limit state [ATC-40 1996][3].The static approximation consists of applying a vertical distribution of lateral loads to a model which captures the material non - linearity of an existing or previously designed structure, and monotonically increasing those loads until the peak response of the structure is obtained on a base shear versus roof displacement plot. Here three static pushover cases are considered. In the first case gravity load is applied to the structure, in the second case lateral load is applied to the structure along X-direction and in the third case lateral load is applied to the structure along Y-direction for the three types of loading patterns
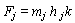 | (1) |
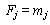 | (2) |
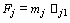 | (3) |
4. Results and Discussion
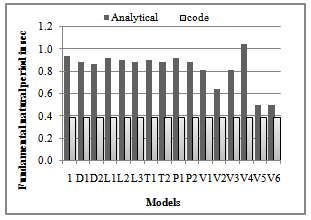 | Figure 2. The Fundamental natural period for 3 storey building models |
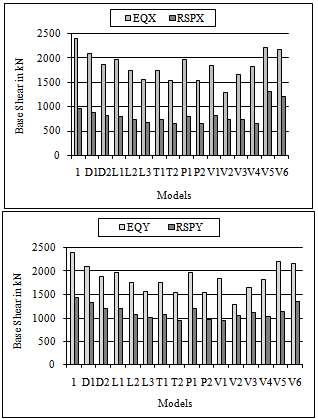 | Figure 3. The Comparison of Base shear for 3 storey building models in X and Y direction |
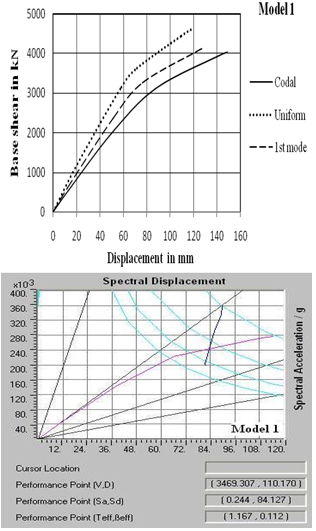 | Figure 4. Pushover curve and Performance point |
5. Conclusions
- 1. The equivalent static method doesn’t consider the irregular effects in the building and since it depends only on empirical formula the results obtained will be abnormal in comparison to response spectrum method.2. The eccentricity between centre of mass and centre of rigidity varies even though in the absence of dual systems i.e. shear walls.3. In pushover analysis the codal type of vertical distribution of lateral force was found more detrimental in low rise models. Since more number of hinges are formed for a given displacement level compared to the other two patterns.4. The performances of all the models except sloping ground (V5 and V6) are lies in between life safety and collapse prevention. This shows the buildings resting on sloping ground are more vulnerable to earthquake than rest of the models.5. The result also shows that, capacity of the buildings may be significant but the seismic demand varies with respect to the configurations.
|
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML