1. The Sorites

“The name ‘sorites’ derives from the Greek word soros (meaning ‘heap’) and originally referred, not to a paradox, but rather to a puzzle known as The Heap: Would you describe a single grain of wheat as a heap? No. Would you describe two grains of wheat as a heap? No. … You must admit the presence of a heap sooner or later, so where do you draw the line?” (Hyde 2005)

Thus, the sorites is a semantic puzzle, since it is about Semantics: the meaning of the word ‘heap’ or ‘soros’ in Greek. Its origins can be traced back to Eubulides of Miletus in the 4^th century BC (400-300 BC).

According to Hyde (2005), it can assume at least three different shapes, one of those being the mathematical induction: the key sigmatoid (Pinheiro 2022, p. 61) in the soritical sequence (‘bald’, ‘heap’, etc.) is seen associated with a world reference (Pinheiro 2022, p. 61) that gets its defining element increasing or decreasing in amount and implications of the type ‘if…then’ appear as ideal for marking the incremental steps.

An example of sorites is that of The Bald (Machina 1976):

“A man with no hair is bald.

If you add just one more hair to a bald man’s head, then he is still bald.

As a result, it must be the case that a man with 10⁷ hairs on his head is bald.”

The argument seems to be successful and have, as its conclusion, a statement that seems obviously absurd and therefore this is a paradox in Quine’s definition (Pinheiro 2024, p. 8).

It seems that vague predicates could all admit of such a sorites paradox (Hyde 2005).

2. In Context: Solutions So Far

Hyde (Hyde 2005) claims that there are four types of strategy people use to solve the paradox:

a) Claiming that Logic doesn’t apply to soritical expressions and therefore claiming that the problem cannot be set up in a legitimate way.

b) Denying one or more premises.

c) Denying the validity of the sorites.

d) Accepting the sorites as sound or embracing it.

Hyde also claims that, for a theory to be a solution to this paradox, it must be able to address all its possible shapes (at least 3) (Hyde 2005).

Solutions split into six philosophical areas: ideal language approaches, epistemic theory, supervaluationism and relatives, many-valued logic, contextualism and relatives and embracing the paradox (Hyde 2005).

Ideal language approaches are those that wish for making language terms be precise (Hyde 2005). They involve claiming that language suffers from some fault (Hyde 2005). That would be a type-A solution (Hyde 2005), since they also claim that Logic does not apply to the problem.

It seems that soritical expressions are unavoidable, though: if we say ‘tall’ is now defined as height of 1.80m, we would have to measure the person before asserting that they are tall even if we want to lie (if we want to lie, we would like to say they are not tall when their height is superior to 1.80m and, if we want to tell the truth, we would like to say they are tall if their height is such). Such seems to be highly unwanted and impossible to deal with in practice.

Vagueness seems to be what makes the entities of the world artistic: how many people would have composed songs and poems or written books or made movies about love? If we make the definition of the term precise in the dictionary, so say love is now sex once a day and companionship 75% of the time, not only people will have to measure that before speaking (regardless of intentions when they speak, so lying or telling the truth) but that seems to be an art killer. We seem to like arts.

Epistemic theories are a type-B solution (Hyde 2005), so that they deny one or more premises of the paradox. Their denial is based on the argument that there is a point where things stop being such (so ‘bald’) but we are currently lacking the knowledge/tool to determine this point.

“Williamson and Sorensen have offered an impressive array of arguments defending an epistemological account of vagueness which, if successful, would make possible an epistemological solution to the sorites” (Hyde 2005), so that it is possible that an account of this type will be universally accepted as solution in the near future.

Supervaluationism and relatives would consist of a type-B solution (Hyde 2005). “Contra an epistemic account, the positive extension of a predicate is given by those objects to which the predicate definitely applies, the negative extension is given by those objects to which the predicate definitely does not apply, and the remaining (borderline) cases constitute the predicate's penumbra.” (Hyde 2005)

This approach does not preserve LEM (Law of the Excluded Middle), since at least some instances of the premise will be part of the gap area or penumbra or indeterminacy (Fine 1975, p. 284).

Supervaluationism, applied to the sorites, means that each precisification would be seen as the result of the assessment by a particular individual of the soritical sequence entities and the individual would then give the premise a ‘true’ or (exclusively) a ‘false’ for each one of those.

Therefore, for each precisification, there is a cut-off point. After collecting all precisifications, the decision of the logical system is then saying that the predicate applies to the entity from the soritical sequence if it does so for all individuals (supertrue). If it doesn’t apply to a particular entity of the soritical sequence for all individuals, then that is superfalse.

The main problem with this theory is that most individuals, if not all of them, will have a penumbra region in their precisification, so that this account solves the problem only for a society of robots whose decisions are always the classical logic ones: either true or false but not both.

Subvaluationism is a theory that is a relative of Supervaluationism and it would also be a type-B solution. It then considers the premise to be subtrue if it is true on some precisifications and subfalse if it is false on some. In the penumbra region, the premises are considered to be both subtrue and subfalse.

“Suppose, for instance, that we have a set of one hundred color samples, Sample No. 1 to Sample No. 100, whose colors gradually change from prototypical red to prototypical orange. According to supervaluationism, it is (super)true that for some n, Sample No. n is red yet Sample No. n+1 is not, but for no particular n is it (super)true that Sample No. n is red and Sample No. n+ 1 is not. According to subvaluationism, Modus Ponens does not hold generally, for if "Sample No. 51 is red" is true on some but not all precisifications and "Sample No. 52 is red" is not true on any precisification, then "Sample No. 51 is red" and "If Sample No. 51 is red, so is Sample No. 52" are both (sub)true, but "Sample No. 52 is red" is not. These anomalies indeed constitute the super- and subvaluational responses to the Sorites Paradox.” (Akiba 1999)

Besides, the same criticism we made to Supervaluationism applies here, since the precisifications go in the same way as those from Supervaluationism, so that we have to say it is not possible for individuals to always have a cut-off point: there is always going to be a penumbra region of some type.

One Many-valued logic is Fuzzy Logic, where an infinity of values is seen. That would then be a type-B or type-C solution, depending on the notion of validity adopted. “Just as baldness comes in degrees so too, it is argued, does the truth of sentences predicating baldness of things. The fact that John is balder than Jo is reflected in the sentence ‘John is bald’ having a higher degree of truth than ‘Jo is bald’.” (Hyde 2005)

“There are a number of problems which beset any infinite-valued approach to vagueness. Firstly, the very idea of a degree of truth needs explanation. Secondly, if numerical truth-values are to be used some justification seems required for the particular truth-value assignments.” (Hyde 2005)

Another example of many-valued logic is the 3-valued logic, which may bring the truth-values true, false and indeterminate. One of the main criticisms to it being a solution to the sorites is that it seems arbitrary to choose a cut-off point, where the soritical sequence entities stop deserving the predicate. Such a problem could be addressed by establishing that asserting both truth and falsehood of an application of a predicate to a soritical sequence entity or neither simply mean confusion of the speaker and therefore we are left with a judgement that cannot be useful, when we call that indeterminate. In this option, we don’t have LEM and contradictions may sometimes be true (Hyde 2005).

Contextualism gives a type-B solution to the sorites in its mathematical induction version (Hyde 2005). It proposes that the sharp boundaries we look for don’t exist (Hyde 2005). “Confronted with any pair of items in a series with regard to which the predicate in question is soritical, the predicate is always interpreted in such a way as to not distinguish between them. For example, ‘heap’ is never interpreted in a context so as to apply to one of an indistinguishable pair of piles of wheat and not the other” (Hyde 2005). “The way is clear to suppose that such boundaries might exist despite their apparent absence (Hyde 2005).”

“Despite every instance of the universally quantified premise being true, the premise itself is false”, says Kamp when solving the sorites by means of adopting a contextualist approach (Hyde 2005). “Raffman retains a standard semantics for the universal quantifier; the conditional sorites is accordingly valid but has some false premise” (Hyde 2005). “Appearances to the contrary fail to properly account for context by failing to notice that truth can be secured for all the conditionals together only by equivocating on context (Hyde 2005). “Stanley (2003) points to versions of the paradox seemingly resistant to a contextualist analysis. If we agree with Soames that such an analysis treats vague terms as indexicals, then a diagnosis of some paradoxical forms by means of equivocation on an implicit contextual parameter is precluded by certain facts about indexicals (Hyde 2005)”.

“In particular, indexicals do not admit of varied interpretation in verb phrase ellipsis. Consider, for example, the statement ‘Jack is tired now and Jill is too’. Both the first and second (implicit) occurrence of the indexical ‘now’ must be given the same interpretation; Jack and Jill are simultaneously tired. As a consequence, versions of the sorites paradox that employ such ellipses, even granting the contextual parameters implicit in the vague predicates, are not open to contextualist resolution. (Hyde 2005)”

If one embraces the paradox, one says that the conditional sorites paradoxes are all sound and they are then adopting a type-D solution (Hyde 2005). In this case, “no amount of grains of wheat makes a heap” (Hyde 2005). However, “such paradoxes come in pairs. There are negative and positive versions depending on whether the soritical predicate is negated or not. To accept all sorites as sound requires assent to the additional claim that, since one grain of wheat makes a heap, any number do. A radical incoherence follows since there is a commitment to all and any number both making a heap and not making a heap. Similarly, everyone is bald and no-one is; everyone is rich and no-one is, and so on. (Hyde 2005)”

“The problem is that the soundness of any positive conditional sorites undercuts the truth of the unconditional premise of the corresponding negative version, and vice versa. Unless one is prepared to countenance the almost total pervasiveness of contradictions in natural language, it seems that not all sorites can be sound. (Hyde 2005)”

3. Our Solution

We propose a nonclassical logic system to solve the sorites and our solution is a type-B one. LEM and the Principle of Non-contradiction are preserved: truth-values are the classical logic ones, so true (1) and false (0), and each premise gets either one or the other but not both.

The Law of Identity is valid, since we will have either v(A)=0 or v(A)=1, exclusively, and the implication is evaluated as in classical logic.

Antecedent Strengthening is valid. So is Transitivity. Contraposition is not valid.

Ex-Falso Quodlibet (EFQ) is embraced: contradictions are always false and therefore imply anything.

Double negation is not always valid because of the cases of the type when you utter A and not-A (confusion): For those cases, v(A)=v(not-A)=0. That means v(not-not-A)=1, which is different from v(A).

The tables are the same as those in classical logic apart from when the individual speaks in a confusional way, since the truth-values will still be classical then, but the table is going to change. Speaking in a confusional way means that they utter both A and not-A or utter nothing involving A, so neither A nor not-A.

There is a clear explanation for the boundaries: it is only when the individual has confused speech that we have to intervene with the translation of their speech into logical entries. Each individual has their own assessment results and therefore is entitled to their own assignment of responses: does this predicate apply or not to this soritical sequence entity? If they answer yes and no at the same time or if they don’t answer, which means they are confused, we put a false (0) as the truth-value for the premise. If a person utters, with no confusion, A, then not-A may still be true or false. If the person says true and false, then we mark that as false and, if they say nothing, we also mark that as false.

Take A and B to be two consecutive soritical sequence premises. We then have the classical logic table for speech that contains no confusion, so, for instance, when the individual utters A but does not utter not-A.

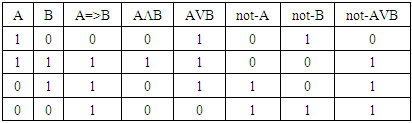When there is confusion, the table will change. Say the individual makes confusion when talking about A but not when talking about B, so they utter A and not-A but utter B only or they utter nothing involving A and utter B only. Because there is confusion when they refer to A, A is false (0). Not-A is also false (0) because there is confusion about A.

The table will then be:

Another possibility, in terms of confusional speech, is that they utter A and not-A plus B and not-B or utter nothing about A and nothing about B or utter nothing about A plus B and not-B or utter A and not-A plus nothing about B. Because there is confusion when they refer to both A and B, A is false (0) and so is B (0).

Yet another possibility, in terms of confusional speech, is that they utter A and not-A plus not-B or they say nothing about A and utter not-B. In this case, there is confusion when they refer to A, so that A is false (0) plus not-A is false as well (0). Not-B was uttered, so that not-B is true (1) and B is false (0).

It is worth observing that if an individual utters not-not A is false or they utter it is both false and true then v(not-not A)=0. In this case, if they utter not-A is false as well, with no confusion, v(not-A)=0.

4. Conclusions

The sorites is a paradox according to the Quinean definition of paradox and it has been around for thousands of years. One of the most famous examples is The Bald.

Several solutions have been presented so far in the literature. They can be grouped into four strategy types: Claiming that Logic doesn’t apply to soritical expressions and therefore claiming that the problem cannot be set up in a legitimate way, denying one or more premises, denying the validity of the sorites and accepting the sorites as sound or embracing it.

They can also be grouped in terms of philosophical areas: ideal language approaches, epistemic theory, supervaluationism and relatives, many-valued logic, contextualism and relatives and embracing the paradox.

Solutions presented so far suffer from a few flaws: contradictions are not necessarily false, LEM is not valid, the assignment of truth-values seems to be arbitrary, the truth-values are unnatural and there are inconsistencies between the theory presented in the solution and the theory that seems to be behind it.

We present a type-B solution that is nonclassical but preserves the truth-values and tables from classical logic apart from when there is confusional speech (the person utters A and not-A or does not utter anything about A). LEM is not valid and whenever there is confusional speech, we give the premise a false (0). Contradictions are false.